
RDF COLLECTIONS
Saket Kaushik and Duminda Wijesekera
Department of Information and Software Engineering, George Mason University, Fairfax, Virginia 22030, U.S.A.
Keywords:
RDF, Ontology, Higher Order Types, Entailment, abstract data types.
Abstract:
We add collection types such as sets, bags and lists to the resource description framework (RDF).
1 INTRODUCTION
The Semantic Web consists of a layered architec-
ture (Burners-Lee et al., 2001) of web languages, and
is hinged on the Resource Description Framework
(RDF) (Brickley and Guha, 2003) for expressing in-
ternet ontologies. Ontology languages abovethe layer
of RDF, such as OWL (McGuinness and van Harme-
len, 2004), DAML etc., add custom syntax to RDF
for expressing ontologies. A different semantics for
each layer/language places severe constraints on in-
teroperability of Semantic Web agents and applica-
tions. Consequently, a need exists for specifying se-
mantics of all Semantic Web languages in terms of a
single language and its semantics – this language is
called L
base
(Guha and Hayes, 2003). It is expres-
sive enough to encompass all current languages and
ensures interoperability between them.
Though highly expressive, L
base
lacks certain de-
sirable features (Guha and Hayes, 2003), like tem-
poral ontologies, version control for ontologies, ade-
quate support for higher-order constructs, etc. Same
is true for its successor specification – RDF Se-
mantics (Hayes and McBride, 2004) and predeces-
sors((Fikes and McGuinness, 2001), etc.). Although
the cited specifications provide a syntax for higher
types like bags, lists, alternatives, etc., they don’t in-
terpret these types. As a result, Semantic Web agents
are unable to deduce useful properties relating to col-
lections. For example, consider the case of a shop-
ping bag (a multiset that may include multiple copies
of members). Suppose each shopping bag item has
an associated price. A useful inference could be the
total cost price for the bag. However, this calcula-
tion/deduction is not currently supported in RDF – a
deficiency addressed in this work.
1.1 Our Contribution
In this paper we model a fragment of RDF that does
not include self references. In addition to the sim-
ple graphs (Hayes and McBride, 2004), we provide
reified graphs syntax with a denotational semantics
to the graph. Additionally, our graphs support three
common higher-order types, viz., sets, sequences and
multisets (bags), that are not currently interpreted
in RDF. We give a system of rewrite rules and in-
clude them in the semantics of reified graphs, closely
strengthening the graph entailments of (Hayes and
McBride, 2004). We show the usefulness of our addi-
tion by using an example.
The paper is organized as follows. We first in-
troduce RDF and the resources in section 2. This is
followed by formalization of collections in Section 3.
Section 4 introduces reified graph definitions that in-
clude higher order types. Semantics of these graphs
are presented in section 5 and graph entailments in
section 6. Section 7 concludes the paper.
2 RESOURCE DESCRIPTION
FRAMEWORK
RDF is used to specify meta-information about re-
sources, i.e., entities that can be uniquely identi-
fied, and binary relations (binary properties between
resources) between them so that they can be “ma-
chine processed”. RDF does so by using the syn-
tax of triples where the subject (the first compo-
nent of the triple) is related by the property (the sec-
ond component of the triple) to the object (the third
component). Commonly, subjects and objects are
91
Kaushik S. and Wijesekera D. (2007).
RDF COLLECTIONS.
In Proceedings of the Third International Conference on Web Information Systems and Technologies - Web Interfaces and Applications, pages 91-97
DOI: 10.5220/0001286500910097
Copyright
c
SciTePress
atomic, i.e., they have no further set-theoretic struc-
ture. However, properties can be extended beyond
connecting atomic objects, i.e., to expressing relation-
ships between properties and atomic objects. This
process, carried out recursively, is called reification.
RDF(S) or RDF Schema is RDFs vocabulary descrip-
tion language. It has syntax to describe concepts
and resources using the meta-syntax of
rdfs:Class
,
rdf:type
, etc., and relationships between resources
through
rdf:property
. These meta classes are used
to specify properties of user defined schema. Details
of RDF/RDF(S) syntax and vocabulary descriptions
can be found in (Brickley and Guha, 2003).
A collection of RDF triples form a graph, i.e., if
the object of a triple is the subject of another triple,
then the two triples are merged together retaining the
common object only once (with one incoming edge
and one outgoing edge). Hayes and McBride (Hayes
and McBride, 2004) give semantics of RDF/RDF(S)
as RDF graphs (informally) using model theory. They
informally state an entailment relationship between
graphs. However, this semantics is lacking in sev-
eral respects. Firstly, they described containers such
as multisets and lists without semantics. As a remedy,
we provide rewrite rules for abstract data type (Har-
rison, 1993) for three collections, viz., sets, bags and
sequences and, correspondingly, extend RDF entail-
ments to include them.
3 CONTAINERS FORMALIZED
Sets, bags and sequences are abstract data types that
support a set of algebraic operations, described next.
In our formulation, a set is a collection of homoge-
neous base types (atomic or otherwise) that does not
allow duplicates or location ordering of its elements.
A bag, or a multi-set, on the other hand is a homoge-
neous collection that may contain duplicates. If T is a
type then we use the notation Bag[T] for the bag type
of objects of type T (respectively, Set[T] for sets). We
write x ∈ B to denote that x is an element in bag B (the
same notation is used for sets). In contrast to sets, the
multiplicity of an element in a bag is the number of
its repetitions in the bag (Grumbach and Milo, 1993;
Albert, 1991; Dayal et al., 1982; Kent, 1989; Mumick
et al., 1990). That is, modeled as a function, referred
to as profile function in the literature, mapping each
member of a bag B to its repetition count (a natural
number); represented in infix notation using the func-
tion symbol A. Thus, for x ∈ B, (x A B) ∈ N
+
(the set
of positive natural numbers). Size of a bag is given
by the number of objects in the bag, counting repe-
titions, and provides a basis for comparison amongst
bags based on their elements.
A sequence (Seq[T]) is a homogeneous collection
with linearly ordered members – an ordering based
on their, so called, location in the sequence. That is,
a function (called the ordering function) maps each
member of a sequence to the set N, represented by µ,
such that for no two distinct objects x, y of a sequence
S satisfies µ
S
(x) = µ
S
(y) (Our rewrite rules don’t
make explicit use of this function). In addition, two
functions head and tail return the first element and
rest of the elements of a sequence, i.e., first(S) = x iff
µ
S
(x) = 1 and last(S) = S’ iff µ
S
′
(y) = (µ
S
(y)−1), for
all y ∈ S, µ
S
(y) 6= 1. Next we provide algebraic specifi-
cations for the collection types (Harrison, 1993) using
the notation x : A for ‘x is of type A’.
Definition 1 (Basic algebra for sets of finite type)
Given base types T
i
(including boolean, N, etc.), the syntax
of operations on sets over T
i
(represented as Set[T
i
]) are:
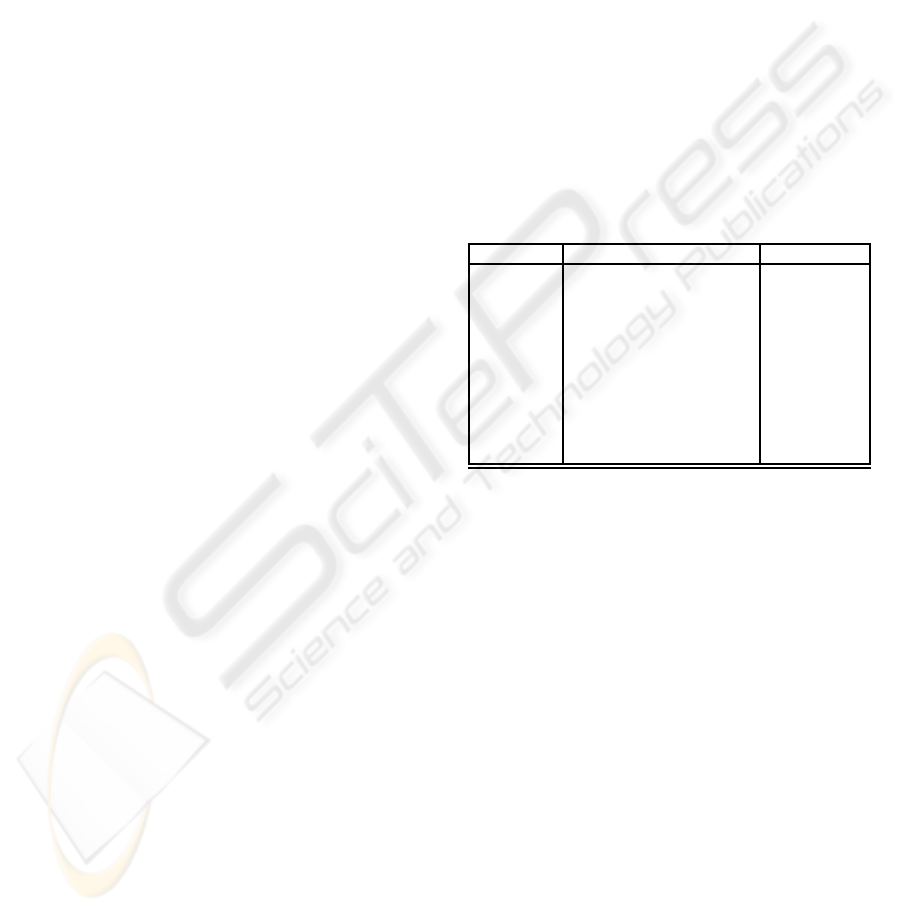
Table 1: Set type.
Operation Type Name
{ x} T
i
→ Set[T
i
] Constructor
ins T
i
× Set[T
i
] → Set[T
i
] Insert
∪ Set[T
i
]× Set[T
i
] → Set[T
i
] Union
∩ Set[T
i
]× Set[T
i
] → Set[T
i
] Intersection
\ Set[T
i
]× Set[T
i
] → Set[T
i
] Minus
∈ T
i
× Set[T
i
] → boolean Membership
⊆ Set[T
i
]× Set[T
i
] → boolean Subset
== Set[T
i
]× Set[T
i
] → boolean Equality
rem T
i
× Set[T
i
] → Set[T
i
] Remove
cnt Set[T
i
] → N Cardinality
Properties of set (a) members, given a is of type Set[T
i
]:
x 6∈ {}
T
i
false
x ∈ a : Set[T
i
] ⇒ x : T
i
b : Set[T
i
] ⊂ a, x ∈ b ⇒ x : T
i
ins(x, a) : Set[T
i
] ⇒ x : T
i
rem(x,a) : Set[T
i
] ⇒ x : T
i
Axiomatic Semantics for operations on sets are as follows:
x ∈ ins(y, z) = true if x=y, x ∈ z otherwise
cnt({ }
T
i
) = 0
cnt(ins(x, z)) = 1+ cnt(z) i f x 6∈ z, cnt(z) otherwise
a ⊂ b = true i f (x ∈ a ⇒ x ∈ b)
false otherwise
a == b = a ⊂ b∧b ⊂ a
rem(x,z) = y such that x ∈ z∧ z = ins(x, y),
z otherwise
a\b = y such that x ∈ y ⇒ x ∈ a∧ x 6∈ b
a∩b = y such that x ∈ y ⇒ x ∈ a∧x ∈ b
a∪b = y such that x ∈ y ⇒ x ∈ a∨ x ∈ b
Basic bag algebra is presented next. Note that we
specify ‘additive union’ operation for bags instead of
WEBIST 2007 - International Conference on Web Information Systems and Technologies
92
the usual set union. This operation adds the total num-
ber of occurrences in the resulting bag.
Definition 2 (Basic algebra for bags of finite type)
Given base types T
i
(including {true, false}: boolean, nat-
ural numbers: N); syntax of operations on bags over types
T
i
are:
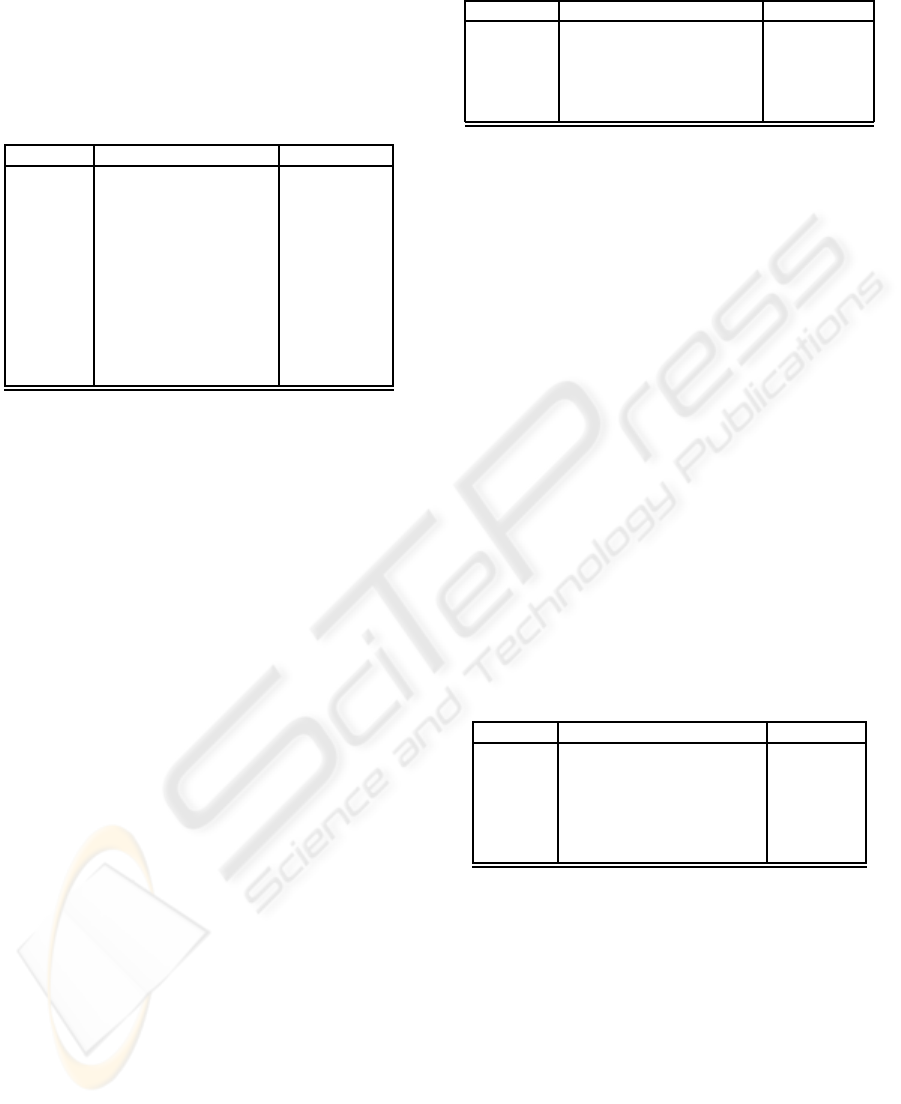
Table 2: Bag type.
Operation Type Name
*x, x, . . . ,x+ T
i
→ Bag[T
i
] Constructor
ins T
i
× N× Bag[T
i
] → Bag[T
i
] Insert
rem T
i
× N× Bag[T
i
] → Bag[T
i
] Remove
∩ Bag[T
i
]× Bag[T
i
] → Bag[T
i
] Intersection
\ Bag[T
i
]× Bag[T
i
] → Bag[T
i
] Minus
⊔
+
Bag[T
i
]× Bag[T
i
] → Bag[T
i
] Additive Union
∈ T
i
× Bag[T
i
] → boolean Membership
A T
i
× Bag[T
i
] → N Profile
F Bag[T
i
]× Bag[T
i
] → boolean Subbag
F Bag[T
i
]× Bag[T
i
] → boolean Proper Subbag
cnt Bag[T
i
] → N Cardinality
Given a bag a of type Bag[T
i
], properties of members
are:
x A * +
T
i
= 0
x ∈ * +
T
i
= false
x ∈ a : Bag[T
i
] ⇒ x : T
i
(x A a : Bag[T
i
]) > 0 ⇒ x : T
i
b D a : Bag[T
i
], x ∈ b ⇒ x : T
i
ins(x, a) : Bag[T
i
] ⇒ x : T
i
rem(x,a) : Bag[T
i
] ⇒ x : T
i
Given x, y ∈ T;n ∈ N;b, b
′
∈ Bag[T], the semantics of oper-
ations is as follows:
x ∈ ins(y, b) = true if x=y, x ∈ b otherwise
x A b = 0 if x 6∈ b
x A ins(x, b) = 1+ x A b
cnt(* +
T
i
) = 0
cnt(ins(x, b)) = 1+ cnt(b)
a D b = true i f (x ∈ a ⇒ x ∈ b) ∧
(x A a < x A b), false otherwise
a F b = true i f (x ∈ a ⇒ x ∈ b) ∧
(x A a ≤ x A b), false otherwise
rem(x,b) = b
′
such that x ∈ b∧ z = ins(x, b
′
),
b otherwise
a\b = b
′
such that x A b
′
=
max(0, (x A a− x A b))
a∩b = b
′
such that x A b
′
= min(x A a, x A b)
a⊔
+
b = b
′
such that x A
′
= (x A a+x A b)
Next we define the algebra of sequences as recur-
sive types that are built over the terminal element –
nil.
Definition 3 (Algebra of sequences) Given base
types T
i
and a constant symbol nil, syntax of operations
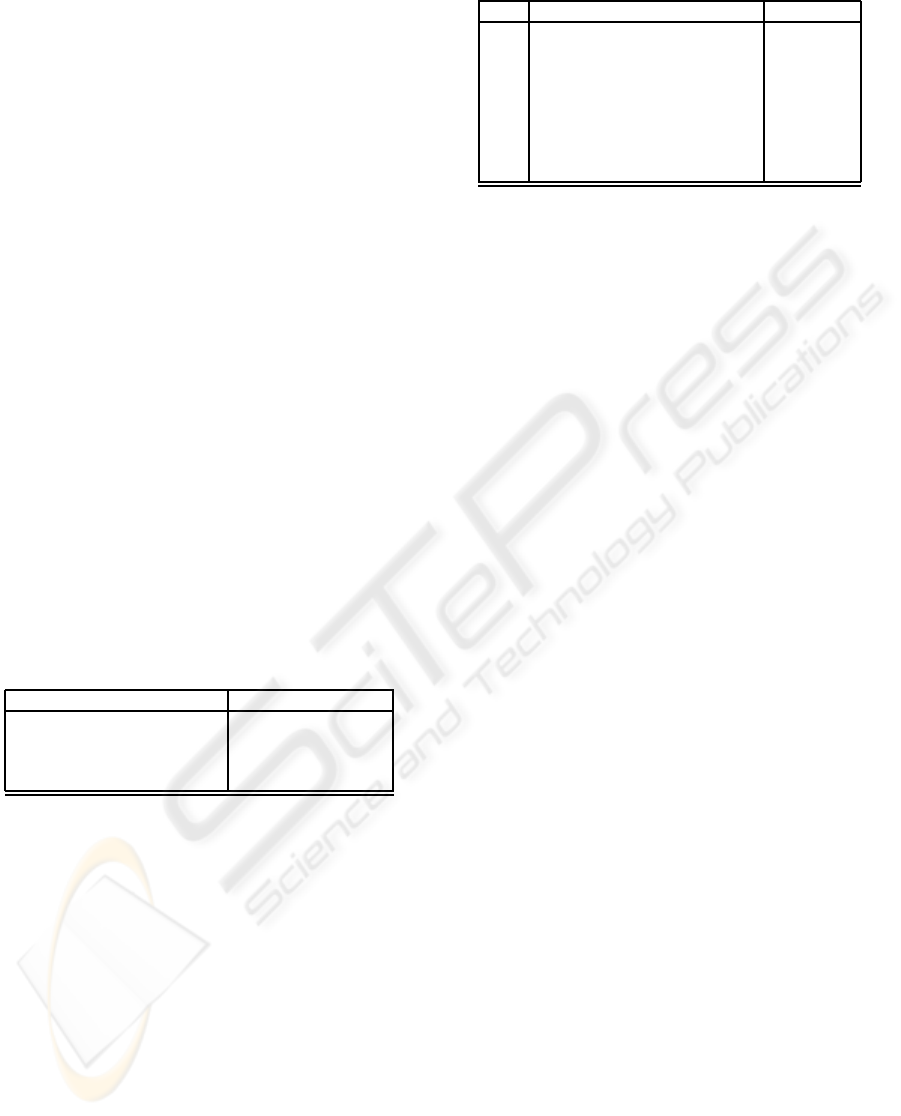
Table 3: Sequence type.
Operation Type Name
hxi T
i
→ Seq[T
i
] Constructor
hd Seq[T
i
] → T
i
Head
tl Seq[T
i
] → T
i
Tail
∈ T
i
× Seq[T
i
] → boolean Membership
== Seq[T
i
] × Seq[T
i
] → boolean Equality
on sequence type (written Seq[T
i
]) are as follows: Given a
sequence a of type Seq[T
i
], properties of members are:
x ∈ a : Seq[T
i
] ⇒ x : T
i
x = hd(a : Seq[T
i
]) ⇒ x : T
i
x = tl(a : Seq[T
i
]) ⇒ x : Seq[T
i
]
Semantics of operations are provided next.
hd(a) = h : T
i
such that ∃t : Seq[T
i
], a = hh.ti
nil otherwise
tl(a) = t : Seq[T
i
] such that ∃h : T
i
, a = hh.ti
hnili otherwise
a == b = ∃h
1
, h
2
: T
i
,t
1
,t
2
: Sequence, a = hh
1
.t
1
i ∧
b = hh
2
.t
2
i ∧ h
1
= h
2
∧t
1
= t
2
x ∈ hnili = false if x 6= nil, true otherwise
x ∈ a = true i f ∃h : T
i
,t : Sequence,x = h∨ x ∈ t
false otherwise
Definition 4 (Algebra of Triples) Given types S, O
and P (type T denotes type S, type O or type P), syntax of
operations on triples is given in table 4. Given a triple a of
Table 4: Triple type.
Operation Type Name
(S, P,O) S×P× O → (S, P,O) Constructor
sub (S, P,O) → S Subject
prp (S, P,O) → P Property
obj (S, P,O) → O Object
∈ T × (S, P,O) → boolean Membership
== (S
′
, P
′
, O
′
) × (S,P, O) → boolean Equality
type S× P× O, properties of members are:
x = sub(a : S× P× O) ⇒ x : S
x = prp(a : S× P× O) ⇒ x : P
x = obj(a : S×P× O) ⇒ x : O
The semantics of operations are given as follows:
sub(x,y,z) = x
prp(x,y,z) = y
obj(x, y, z) = z
u ∈ (x, y,z) = true if u = x∨ u = y∨ u = z, false otherwise
a == b = true if sub(a) = sub(b) ∧ prp(a) = prp(b)
∧obj(a) = ob j(b), false otherwise
RDF COLLECTIONS
93
4 FORMALIZING RDF
We formalize RDF as a collection of higher typed ob-
jects and binary relations among them, constructed
from a set of atomic types over a universe of objects,
U, using a set of (polymorphic) type construction op-
erators as suggested in RDF (Hayes and McBride,
2004). Three different types of collections can be
formed from atomic elements, viz., sets, bags and se-
quences, defined earlier.
RDF consists of schema and instances in a layered
manner. Elements of each layer include objects con-
structed from the set of atomic objects U, using the
set constructor, { }, the bag constructor, * + and the
sequence constructor, h i. These functions form the
set of constructors, called Σ. Depending upon the re-
quirements, ontology modelers can use any subset of
the set of type constructors. This set of atomic objects
is called the set of primary nodes. Primary edges of
the graph are formed from the pairs of primary nodes.
Because of the possibility of reified graphs, the set of
triples in a graph may consist of pairs of nodes and
triples as well, defined next.
Definition 5 (Algebra for Nodes and Triples)
Given a set of atomic types U, a set of boolean values
B, integers N and a set of collection constructors – {
{ }, * +, h i} over U, collectively called collections and
represented by the type C, we inductively define nodes (N
i
)
and triples (Tr
i
) in table 5. Properties of nodes and edges
Table 5: Nodes and Triples.
Type Name
x : U ∪x : C[U] → N
0
Node 0 Constructor
y : (N
0
×U × N
0
) → Tr
0
Triple 0 Constructor
x : (C[N
i−1
] ⊔
−
C[Tr
i−1
)] → N
i
Node i Constructor
y : (N
i
×U × N
i
) → Tr
i
Triple i Constructor
are presented next.
x ∈ Tr
i
⇒ sub(x) ∈ N
i
∧ obj(x) ∈ N
i
x ∈ Tr
i
⇒ prp(x) 6= sub(x) ∧ prp(x) 6= obj(x)
{Question: Self references are allowed. Should this
be changed?}
Definition 6 (Algebra for RDF) Given a universe
U,and nodes and triples defined over this universe, we
define a graph as a set over U with following operations:
Properties of graphs are presented next.
x : GR AP H ⇒ y ∈ sub
0
(x) → y ∈ N
0
x : GR AP H ⇒ y ∈ sub
i
(x) → y ∈ sub
i−1
(x) ∨ prp
i−1
(x)
x : GR AP H ⇒ y ∈ obj
0
(x) → y ∈ N
0
x : GR AP H ⇒ y ∈ obj
i
(x) → y ∈ obj
i−1
(x) ∨ prp
i−1
(x)
x : GR AP H ⇒ y ∈ trp
i
(x) → y ∈ Tr
i
x : GR AP H ⇒ ∃k : N|Tr
k
(x) = {}
z = x∪y ⇒ trp
i
(z) : Tr
i
,trp
i
(z) ⊆ trp
i
(x) ∪ trp
i
(y)
Table 6: Graph type.
Opn Type Name
{x} Tr → GR AP H Constructor
sub
i
GR AP H → Set N
i
nodes
obj
i
GR AP H → Set N
i
nodes
trp
i
GR AP H → Set Tr
i
triples
∪ GR AP H × GR AP H → GR AP H Merge
\ GR AP H × GR AP H → GR AP H Minus
⊲ GR AP H × GR AP H → boolean Subgraph
=
s
GR AP H × GR AP H → boolean Equality
The semantics of operations are as follows:
sub
i
(a∪b) = sub
0
(a) ∪sub
0
(b)
obj
i
(a∪b) = obj
0
(a) ∪obj
0
(b)
trp
i
(a∪b) = prp
0
(a) ∪trp
0
(b)
sub
i
(a\b) = sub
i
(a) \sub
i
(b)
obj
i
(a\b) = obj
i
(a) \obj
i
(b)
trp
i
(a\b) = trp
i
(a) \trp
i
(b)
a⊲ b = true if trp
i
(a) ⊆ trp
i
(b)
a =
s
b = a⊲ b∧ b⊲ a
Equality relation ‘=
s
’, defined above, equates ‘struc-
turally equivalent’ graphs. That is, two graphs are
structurally equal if they have exactly the same struc-
ture (based on the equality relation of constituent
types). RDF also allows name-based equality, which
we cover in the next section.
4.1 Named RDF Graphs
To enable name-based equality of RDF graphs, we in-
troduce names for graph elements.
Definition 7 (Names) Let U be a universe of objects.
Named Graph We use a set of names, called
N AM ES and a naming function N from Graph
to N AM ES ∪ (⊥ × N) (where (⊥ × N) repre-
sents a blank node and its ‘node Id’ (Hayes and
McBride, 2004)) that maps each node and prop-
erty in an RDF graph to its name. We abuse the
notation slightly to say N (x) = ⊥ if a node is a
blank node.
Ground Graph A graph that has no nodes mapped
to ⊥.
Next, we define name-based equality of graphs.
With structural equality as a prerequisite, blank nodes
at similar structures are assumed to be equal). This is
followed by the definition of graph instances.
Definition 8 (Name-based Equality ‘=
n
’) Two
graphs f and g, with name maps N and N
′
, are said
to be name-wise equal, i.e., f =
n
g, if f =
s
g and
∀i(t ∈ trp
i
( f) ⇒ ∃t
′
∈ trp
i
(g)|N (prp(t)) = N
′
(prp(t
′
))∧
N (sub(t)) = N
′
(sub(t
′
)) ∧ N (obj(t)) = N
′
(obj(t
′
))).
WEBIST 2007 - International Conference on Web Information Systems and Technologies
94

Definition 9 (Instance) A graph a with naming function
N is said to be an instance of graph b (naming function
N
′
) if
• ∀i(x ∈ (sub
i
(b) ∪ obj
i
(b) ∪ prp(trp
i
(b))) ∧ N
′
(x) 6=
⊥ ⇒ ∃y ∈ (sub
i
(a) ∪ obj
i
(a) ∪ prp(trp
i
(a)))|N
′
(x) =
N (y)).
• ∀i(x ∈ (sub
i
(b) ∪ obj
i
(b) ∪ prp(trp
i
(b))) ∧ N
′
(x) =
⊥ ⇒ ∃y ∈ (sub
i
(a) ∪ obj
i
(a) ∪ prp(trp
i
(a)))|N (y)) ∈
N AM ES ∪ ⊥ .
We are now in a position to express basic col-
lection types in RDF. We use available syntax for
expressing bag and sequence types, i.e.,
rdf:Bag
and
rdf:Seq
, and introduce
rdf:Set
to express Set
types. Next we formalize the shopping bag example
discussed earlier.
Example 1 Consider a group of atomic, named RDF
nodes (subjects). Eachof the resource has a property named
‘value’, i.e., domain(value)= nodes and range(value)= N.
(RDF syntax for describing these triples is straightfor-
ward and is omitted here). We assume N admits simple
arithmetic (addition function and equality predicate) (Pres-
burger, 1929). Consider now a
rdf:Bag
type resource with
each of above described resources as its members. We call
this bag a ‘shopping bag’. Since each member has some
numeric value, we can describe a higher-order property,
named ‘total’, based on the ‘value’ property of the mem-
bers using simple addition over values. That is, we can
now express a triple with property name ‘total’ such that
domain(total) = Bag[ShoppingItems] and range(total)= N.
5 SEMANTICS
In this section we provide limited semantics for fi-
nite types introduced earlier. To do so we start with
a universe, i.e., a set of URI’s (denoted URI) and
other constants, say B as urelements (i.e., those atomic
elements that do not have any further structure to
them (Aczel, 1988; Kunen, 1983)). There is no URI
corresponding to blank nodes. In the following P rep-
resents powerset operator. Hierarchical universe is
built as follows:
N
0
and P
0
:
N
0
= {(u, b) : u ∈ URI and b ∈ B}
P
0
= {(u, (b,b
′
)) : u ∈ URI and b, b
′
⊆ B}
N
n+1
and P
n+1
: Suppose N
n
and P
n
have been defined.
Let U
n
= {x : ∃u ∈ URI(u, x) ∈ N
n
}. Then define
N
n+1
= {(u, B) : u ∈ URI and
B ⊆ P (U
n
) ∪ B(U
n
) ∪ S(U
n
)}
P
n+1
= {(u, (B, B
′
)) : u ∈ URI and
B, B
′
⊆ P (U
n
)
We use this stratified named universe to interpret
RDF graphs and related syntax as follows:
Definition 10 (Semantic mapping J K)
Universe:
1. Suppose U is the universe as defined in definition 7.
2. Let J K
u
:U 7→ B be the surjective mapping that maps
the constants in the syntax to a set B of urelements
over which the syntax is interpreted.
3. Let JK
name
: N AM ES 7→ URI be a mapping of RDF
names to URIs.
Mapping nodes: Every node n ∈ N
n
named a is mapped
as J(a,n)K = (JaK
name
, JnK) where JnK is constructed by
replacing every u ∈ U in n with JuK.
Mapping properties: For every property p ∈ P
n
named a
is mapped as J(a, p)K = (JaK
name
, JpK) where JpK is
constructed by substituting every u ∈ U in p with JuK.
Interpreting triples: For every triple (s, p, o) ∈ Tr
n
is in-
terpreted as J(s, p, o)K = JsK∧ JpK ∧ JoK.
Interpreting rdf:type: We say that Jx, rdf:type, yK iff
x = (a, b), y = (p, q) and JbK ∈ JqK.
Interpreting rdfs:subClassOf: Jx, rdfs:subClassOf,
yK iff x = (a, b), y = (p, q) and JbK ⊆ JqK.
Interpreting names: The name of an object or a property
x is defined as the first coordinate of JxK.
Interpreting intensional equality: x is said to be inten-
sionally equal to y (written x =
int
y) iff JxK = JyK
Interpreting structural equality of nodes and properties:
x is said to be structurally equal to y, written x =
str
y
iff (a,b) = JxK, (p, q) = JyK and b = q.
Interpreting structural equality of triples: (s, p, o) is
said to be structurally equal to (s
′
, p
′
, o
′
), written
(s, p, o) =
str
(s
′
, p
′
, o
′
) iff J(s, p, o)K ∧ J(s
′
, p
′
, o
′
)K ∧
s =
str
s
′
∧ p =
str
p
′
∧ o =
str
o
′
Interpreting intensional equality of triples: (s, p, o) is
said to be intensionally equal to (s
′
, p
′
, o
′
), written
(s, p, o) =
int
(s
′
, p
′
, o
′
) iff J(s, p, o)K = J(s
′
, p
′
, o
′
)K
Interpreting ground graph: Ground graph J{(s, p, o)}K
interpretation is constructed by interpreting each triple
in the graph as {J(s, p, o)K}
Interpreting structural equality of graphs: A graph g is
structurally equal to a graph g
′
iff for each triple t ∈ g
there exists exactly one triple t
′
∈ g
′
such that t =
str
t
′
.
Interpreting graph: Graph JgK is interpreted if
• ∃g
′
: GR AP H such that g
′
is ground and Jg
′
K is
interpreted and
• g =
str
g
′
and
• For all ground triplest ∈ g there exists a triple t
′
∈ g
′
such that t =
int
t
′
and for all triples t ∈ g if sub(t) or
obj(t) is ground, then there exists a triple t
′
∈ g
′
such
that t =
str
t
′
and sub(t) =
int
sub(t
′
) or obj(t) =
int
obj(t
′
).
6 GRAPH ENTAILMENTS
In this section we make precise Hayes and
McBride’s (Hayes and McBride, 2004) informal
treatment of graph entailments that include higher or-
der constructs.
RDF COLLECTIONS
95

Definition 11 (Entailment) We say that a graph g en-
tails another graph g
′
if Jg
′
K ⊆ JgK. We write this as g ⊢ g
′
.
Otherwise we say g does not entail g
′
, i.e., g 6⊢ g
′
Graph entailments simply state the satisfiability of
a graph given a related graph is satisfied. Since we
consider finite graphs, compactness is easily shown.
Lemma 6.1 (Graph Entailments) Hayes and
McBride’s (Hayes and McBride, 2004) results hold
in our framework:
Empty graph entailment Given g:GR AP H , g en-
tails empty graph, i.e., g ⊢ {}
Empty graph Given g:GR AP H and g is not an
empty graph, g is not entailed by empty graph,
i.e., {} 6⊢ g
Subgraph entailment Given g,f:GR APH and g ⊲
f, then g ⊢ f.
Instance entailment Given g,f:GR AP H and g is
an instance of f, then g ⊢ f.
Merging (L) Given g,f:GR AP H then g∧ f ⊢ g∪ f.
Merging (R) Given g,f:GR APH then g∪ f ⊢ g∧ f.
Interpolation entailment Given f,h:GR AP H , g
i
:
GR APH ,(i ≤ n) (
i
g
i
) ⊲ f and f is an instance
of h then (
i
g
i
) ⊢ h.
Monotonicity Given g,f,h:GR AP H , g⊲ f and f ⊢
h then g ⊢ h
Proof Sketch:
Empty graph entailment Let g:GR AP H and g =
{}. Now,
/
0 ∈ JgK.
Empty graph Let g:GR AP H , g 6= {}. By defini-
tion, JgK 6=
/
0.
Subgraph entailment Let g,f:GR AP H and g ⊲
f ⇒ Tr
i
(g) ⊆ Tr
i
( f). Let N be the naming func-
tion for g. Given JgK is interpreted, JfK can be
interpreted with N as the naming function.
Instance entailment Let g,f:GR AP H , g instance
of f and N , N
′
the respective naming functions.
JgK is interpreted; by definition ∀x ∈ sub(trp
i
( f))
such that N
′
(x) 6= ⊥(∃y ∈ sub(trp
i
(g)) such
that y =
str
x ∧ N
′
(x) = N (y)). Now, ∀x ∈
sub(trp
i
( f)) such that N
′
(x) = ⊥, define JxK =
Jy such that y ∈ sub(trp
i
(g)), y =
str
xK. Similar
construction is possible for objects and properties.
Merging L By definition, if g
1
, g
2
: GR AP H , then
∀i(trp
i
(g
1
∪ g
2
) = trp
i
(g
1
) ∪ trp
i
(g
2
)). Clearly,
with N
∪
= N
g
1
∪ N
g
2
it is easy to show g
1
∧ g
2
⊢
g
1
∪ g
2
. This result is easily extended to a set of
graphs.
Merging R Shown in the similar way as in previous
case.
Interpolation entailment Shown similarly using
subgraph, instance and merging lemmas.
Monotonicity Shown similarly using subgraph
lemma.
Next we state an entailment relation for collec-
tions. That is, given a property for a collection of
objects, and allowing a simple arithmetic (Presburger
arithmetic (Presburger, 1929)) we can infer a higher
order property for the collection.
Lemma 6.2 (Collection Entailment) g:GR AP H ,
x:C[T] for some T, for some i ∀x : C[T] ∈ sub
i
(g)(∃t ∈
Tr
i
|sub(t) = x∧ prp(t) = p), where p is some mathematical
function
g, ∀x(x ∈ sub
i
(g) :C[T](∃t ∈ Tr
i
(g), prp(t) = p, sub(t) = x))
∀x(x :C[T], p(x) = n → p
′
(C[T]) = N)
⊢
g∪ {(C[T], p
′
, N)}, where p
′
is a function and
(C[T], p
′
, N) ∈ Tr
i+i
(g∪{(C[T ], p
′
, N)})
Proof Sketch: Follows from subgraph lemma and ba-
sic arithmetic.
Collection entailment states that if there is a graph,
say g, containing a node, say n, that is a collection
(set, bag or a sequence) and each of its members have
an arithmetic property, then g entails a graph that ex-
presses a collective property for n in addition to all
other properties expressed by g. This property is de-
rived by basic arithmetic over the lower order arith-
metic properties. We revisit our running example to
show collection entailment in action. We omit RDF
syntax in our example, however, it is easily checked
that a simple translation to RDF syntax exists.
Example 2 Consider an RDF graph g with some k level
nodes, x
i
, i ≤ n : N such that for each x
i
there is a node
y
i
that is a number (literal), related to x
i
through a property
ψ
k
. Also, there is a k+ 1 level node X of type
rdf:Bag
, with
each x
i
as its member. This graph models the shopping bag
in example 1, where each member of abag has some number
value, expressed as a ‘value’ triple. Since this property is
functional, we can use a function to represent such edges.
That is, we express ψ
k
as a function h(x) := x ∈ X → N for
all members x
i
of the bag X. Clearly, it’s easy to compute
the total value of all the items stored in X by adding them
all together:
h
′
(X) = ∀x ∈ X(
∑
x
h(x))
Thus, h
′
is a function whose domain is a shopping bag
with number valued items as members and range is
N. That is, we can now express a k + 1 level prop-
erty for a collection type, expressible in an RDF graph
using some edge, say ψ
k+1
. More concretely, sup-
pose X is *apple, orange,orange+ and graph g has edges
value(apple, 5) and value(orange, 10). Then, using basic
arithmetic, we can deduce an edge total(X, 5+10+10) or to-
tal(X, 25).
Using the collection entailment lemma, we are able to
deduce a new graph fromg, with an additional edge of name
‘total’ connecting X with a node named 25.
WEBIST 2007 - International Conference on Web Information Systems and Technologies
96

7 CONCLUSION
RDF syntax allows for ontologists to express higher-
order types like sequences, bags and alternatives.
These collections are essential for representing many
real world facts like work flows, shopping bags, pay-
ment receipts, etc. Although collections can be ex-
pressed, but they are not interpreted in RDF. Conse-
quently, Semantic Web agents cannot deduce many
useful inferences based on these collections.
Authoritativespecifications of RDF syntax and se-
mantics (Guha and Hayes, 2003; Hayes and McBride,
2004) acknowledge the need for building these infer-
ences into RDF, however, to the best of our knowl-
edge, this deficiency has not yet been addressed in
the literature. In this paper, we provide an approach
to construct three higher-order types, viz., sets, bags
and sequences. We integrate these types into a reified
RDF framework with a hierarchical semantics. To in-
corporate collections into graph entailments, we for-
malize graph entailments (Hayes and McBride, 2004)
with collections in reified graphs and prove collec-
tion entailments for incorporating deductions based
higher-order types.
REFERENCES
Aczel, P. (1988). Non-well-founded sets, volume 14 of Lec-
ture Notes. CSLI.
Albert, J. (1991). Algebraic properties of bag data types.
In 17th International conference on Very Large Data-
bases, pages 211–219.
Brickley, D. and Guha, R. (2003). Resource Description
Framework (RDF) Schema Specification 1.0: RDF
schema. W3C workding Draft.
Burners-Lee, T., Hendler, J., and Lassila, O. (2001). The
semantic web. Scientific American.
Dayal, U., Goodman, N., and Katz, R. H. (1982). An ex-
tended relational algebra with control over duplicate
elimination. In 1st ACM SIGACT-SIGMOD sympo-
sium on Principles of database systems, pages 117–
123.
Fikes, R. and McGuinness, D. L. (2001). An axiomatic se-
mantics for rdf, rdf-s, and daml+oil. Technical Report
Note 18, World Wide Web Committee (W3C).
Grumbach, S. and Milo, T. (1993). Towards tractable al-
gebras for bags. In Twelfth ACM SIGACT-SIGMOD-
SIGART Symposium on Principles of Database Sys-
tems, pages 49–58.
Guha, R. and Hayes, P. (2003). LBase: semantics for lan-
guages of the semantic web. W3C workding Draft.
Harrison, R. (1993). Abstract Data Types in Standard ML.
John Wiley and Sons.
Hayes, P. and McBride, B. (2004). RDF semantics. W3C
Recommendation.
Kent, W. (1989). Profile functions and bag theory. Tech-
nical Report HPL-SAL-89-19, Hewlett-Packard Lab-
oratories, Palo Alto, CA.
Kunen, K. J. (1983). Set Theory. North Holland, Reprint
edition.
McGuinness, D. L. and van Harmelen, F. (2004). OWL
web ontology language. http://www.w3.org/TR/owl-
features/.
Mumick, I., FinkelStein, S., Pirahesh, H., and Ramakrish-
nan, R. (1990). Magic is relevant. In ACM SIG-
MOD international conference on Management of
data, pages 247–258.
Presburger, M. (1929). Ueber die vollstaendigkeit eines
gewissen systems der arithmetik ganzer zahlen, in
welchem die addition als einzige operation hervortritt.
In Comptes Rendus du I congrs de Mathmaticiens des
Pays Slaves, pages 92–101, Warsaw, Poland.
RDF COLLECTIONS
97
