SCUBA DIVER: SUBSPACE CLUSTERING

OF WEB SEARCH RESULTS

Fatih Gelgi, Srinivas Vadrevu and Hasan Davulcu

Department of Computer Science and Engineering, Arizona State University, Tempe, AZ, U.S.A.

Keywords:

Web search, subspace clustering, guided search.

Abstract:

Current search engines present their search results as a ranked list of Web pages. However, as the number of

pages on the Web increases exponentially, so does the number of search results for any given query. We present

a novel subspace clustering based algorithm to organize keyword search results by simultaneously clustering

and identifying distinguishing terms for each cluster. Our system, named Scuba Diver, enables users to better

interpret the coverage of millions of search results and to reﬁne their search queries through a keyword guided

interface. We present experimental results illustrating the effectiveness of our algorithm by measuring purity,

entropy and F-measure of generated clusters based on Open Directory Project (ODP).

1 INTRODUCTION

Current search engines present their search results as

an ordered list of Web pages ranked in terms of their

relevance to the user’s keyword query. As the number

of pages on the Web is increasing exponentially, the

number of search results for any given query is also

increasing at the same rate. For example there are 544

million results returned by Google search engine

for

the keyword query ‘apple’. Therefore even though

there are millions of potentially relevant documents

for any given user’s query and interest, only top few

ranking documents in the ﬁrst few pages of a search

engine results can be found and explored.

An alternate way to browse the search results re-

turned by a search engine is to organize them into re-

lated clusters to guide the user in her search. When

the search results are clustered and organized in terms

of their distinguishing features, it may become easier

for users (i) to interpret the coverage of millions of

search results and (ii) to reﬁne their search queries.

Traditionally, clustering has been applied to Web

pages in the context of document clustering such as

Clusty

and Mooter

. They have fair performance

and cluster descriptions are not identiﬁed in these sys-

http://www.google.com

http://www.clusty.com

http://www.mooter.com

Figure 1: Clustered results for keyword query ‘apple’.

tems. (Crescenzi et al., 2005) utilizes the structure

of HTML pages to cluster them. They utilize lay-

out and presentation properties of blocks of similarly

presented links in identifying clusters of Web pages.

Their clustering algorithm is based on the observation

that similar pages share the same layout and presenta-

tion structures.

In this paper, we present a way to organize the

search results by clustering them into groups of Web

pages that belong to the same category. Subspace

clustering (Parsons et al., 2004) is an extension of tra-

ditional clustering that seeks to ﬁnd clusters in dif-

ferent subspaces of feature space within a data set.

We choose subspace clustering since it provides the

distinguishing features that make up each cluster, in

334

Gelgi F., Vadrevu S. and Davulcu H. (2007).

SCUBA DIVER: SUBSPACE CLUSTERING OF WEB SEARCH RESULTS.

In Proceedings of the Third International Conference on Web Information Systems and Technologies - Web Interfaces and Applications, pages 334-339

DOI: 10.5220/0001288503340339

 SciTePress

addition to clustering the documents. These features

can be used as additional guidance information in or-

ganizing the search results.

Figure 1 illustrates the keyword query ‘apple’ and

the clusters of Web pages along with their subspace

labels. We reﬁne the clusters obtained by subspace

clustering by merging similar clusters and partition-

ing them so that each Web page belongs to only one

cluster. The ﬁgure also shows the related keywords

comprising all labels, ordered in terms of their occur-

rence frequency. These keywords provide an addi-

tional way to ﬁlter and navigate through the search re-

sults. Figure 1 shows top four clusters along and their

subspaces for the keyword query ‘apple’ after ﬁlter-

ing the subspaces with the keyword ‘computer’ from

the related keywords area. The individual results of

any matching cluster can be displayed by clicking on

the corresponding subspace.

Related work includes clustering techniques have

been used previously in the area of information re-

trieval to organize the search results. (Zeng et al.,

2004) models the search result clustering problem as

ranking salient phrases extracted from the search re-

sults. The phrases (cluster names) are ranked by us-

ing a regression model with features extracted from

the title and snippets of search results. (Beil et al.,

2002) works on frequent-term based text clustering.

One of their data set is collected from Yahoo! subject

hierarchy classiﬁed into 20 categories with 1560 Web

pages. Their best F-measure is 43% for the Web data

which is substantially low compared with their exper-

iments on text documents. Other researchers (Leouski

and Croft, 1996; Leuski and Allan, 2000) utilize tra-

ditional machine learning based clustering algorithms

to cluster the search results and choose descriptive

cluster names from various frequency based features

of the documents.

The rest of the paper is organized as follows.

Problem description and formalization is given in

Section 2. Details of our algorithm is presented in

Section 3 and the experiments is presented in Section

4. We conclude and give the future work in Section 5.

2 PROBLEM DESCRIPTION

In large datasets such as Web, clustering algorithms

have to deal with two challenges as indicated in

(Agarwal et al., 2006): (i) sparsity – the data is sparse

if most of the entries of vectors are zero, (ii) high-

dimensional data – the number of features in dataset

is large. In the Web domain, we have both problems

since the features are terms in the domain, and a Web

page is related with a very small fragment of this term

set. Classical clustering techniques use feature trans-

formation and feature selection to overcome the de-

scribed problems above. On the other hand, newer

techniques such as subspace clustering (Parsons et al.,

2004) localizes its search and is able to identify clus-

ters that exist in multiple, possibly overlapping sub-

spaces instead of examining the dataset as a whole.

Subspace clustering also uncovers the relevant fea-

tures of the clusters and keeps the original ones that

make the interpretation easier.

Context can be deﬁned as the subset of terms in

the domain. Hence one can consider context as the

subspace of the Web pages in the same cluster. In

our formalization, F refers to the feature set selected

from all the terms in the collection of Web pages.

Deﬁnition 1 (Subspace Cluster) A subspace cluster

is a cluster C = hf, wi composed of a pair of sets

where f ⊆ F is the feature set (or the subspace) of

the cluster and w ⊆ W is the set of Web pages be-

longing to the cluster. We denote f (C) and w(C) as

the features and Web pages of a cluster respectively.

Formal deﬁnition of our problem can be stated as:

Problem statement 1 Given a set of Web pages

W = {W

, W

, . . . W

} resulting from an ambigu-

ous keyword search K, ﬁnd the clusters of Web pages

together with their descriptive terms. A Web page W

is deﬁned as the set of the its terms.

This problem can be reduced a subspace cluster-

ing problem as follows:

Problem statement 2 Given a binary n × m ma-

trix M , where rows represent n Web pages (W =

, D

, . . . D

}) and columns represent m terms

(F = {t

, t

, . . . t

}), ﬁnd subspace clusters of Web

pages, W ⊆ W deﬁned in the subspace of terms,

T ⊆ F.

Here D

= hd

, d

, . . . d

i represents the bi-

nary vector of the Web page W

where d

= 1 when

∈ W

. In the matrix M, d

correspond to the entry

in the i

row and j

column, that is M

= d

3 SCUBA DIVER ALGORITHM

Our subspace clustering algorithm given in Algo-

rithm 1 is composed of three steps: feature selection,

subspace clustering, and merging and partitioning.

3.1 Feature Selection

This step is given the ﬁrst line in ScubaDiver func-

tion (ScubaDiver refers to the main function of the

algorithm) in Algorithm 1. SelectF eatures function

SCUBA DIVER: SUBSPACE CLUSTERING OF WEB SEARCH RESULTS

335

Algorithm 1 Clustering of Web Search Results

ScubaDiver(W, K)

Input: K, the search keyword; W, a set Web pages resulting from keyword

search K

Output: C, set of subspace clusters of the Web pages W

1: F ← SelectF eatures(

W ∈W

W )

2: for ∀W

∈ W

3: for ∀t

∈ F

4: if t

∈ W

then M

← 1

5: else M

← 0

6: C ← SCuBA(M, α, β)

7: C ← M erge(C, δ, ξ)

8: C ← P artition(W, C)

9: return C

End of ScubaDiver

Merge(C, δ, ξ)

Input: C, subspace clusters; δ, threshold for the common features; ξ,

threshold for the common Web pages;

Output: C, set of merged subspace clusters of the Web pages W

1: for ∀C

∈ C

2: for ∀C

∈ (C − {C

})

3: if (Jaccard(f(C

), f(C

)) > δ)∧

4: (Jaccard(w(C

), w(C

)) > ξ) then

5: C

′

← hf (C

) ∪ f (C

), w(C

) ∪ w(C

6: C ← C − {C

, C

} ∪ {C

′

}

7: return C

End of Merge

P artition(W, C)

Input: W, set of Web pages; C, subspace clusters;

Output: C, set of partitioned subspace clusters of the Web pages W

1: for ∀W

∈ W

2: closest ← arg max

∈C

{similarity(v(C

), v(W

))}

3: w(closest) ← w(closest) ∪ {W

}

4: C

′

← {X|X ∈ (C − {closest}) ∧ W

∈ w(X)}

5: for ∀C

∈ C

′

6: w(C

) ← w(C

) − {W

}

7: return C

End of Partition

selects features for clustering among all the terms ap-

peared in the data.

In SelectF eatures function, data has ﬁrst been

preprocessed then features have been selected by

three common frequency based methods in Informa-

tion Retrieval (IR). Term frequency of a term t is,

T F (t) =

k∈F

where n

is the number of occur-

rences of t in the domain. Document frequency of t is,

DF (t) =

|D(t)|

where D(t) is the set of Web pages

t appears. A common variation of Term frequency /

inverse document frequency of t is, T F/IDF (t) =

T F (t). lg

DF (t)

. Readers should note that deep anal-

ysis of feature selection is out of scope of this paper.

Based on the three measures abovethe features are

selected as top-m ranked terms among all the terms

in the data excluding the search keyword K. For ex-

ample, top-10 TF/IDF terms obtained from the Web

pages with the search keyword apple in our experi-

ments are ‘mac’, ‘recipe’, ‘ipod’, ‘search’, ‘software’,

‘computer’, ‘macintosh’, ‘list’, ‘store’ and ‘pie’.

3.2 Subspace Clustering

Due to its efﬁciency and effectiveness on binary data,

we use the subspace clustering algorithm SCuBA de-

scribed in (Agarwal et al., 2006) which is part of an

article recommendationsystem for researchers. In Al-

gorithm 1, lines from 2 to 5 prepare the binary matrix

M for SCuBA and line 6 generates the subspace clus-

ters. SCuBA works in two steps: (i) it compacts the

data by reducing the n × m matrix to n rows each of

which is a list of the size of its corresponding Web

page, and (ii) it searches for the subspaces by com-

paring each row to the successive rows to ﬁnd the in-

tersecting rows and their subsets of columns.

SCuBA produces many small subspace clus-

ters with many overlapping Web pages. Exam-

ple of two subspace clusters generated from apple

search have {macintosh, computer, imac, mac}

and {macintosh, check, mac} as their feature sets

containing 4 Web pages each, 2 of which are com-

mon.

3.3 Merging and Partitioning

Final clusters are determined after merging step as the

post-processing on subspace clusters in lines 7 and 8

in Algorithm 1. In the Web data subspace clusters

obtained from SCuBA are in the form of sub-matrices

which are not signiﬁcant in number and size. Clusters

needs to be relaxed to have irregular shapes and to

cover more data as opposed to strict sub-matrices.

A common scenario is the overlapping subspace

clusters which are the subsets of the same actual clus-

ter and the context. Hence it is reasonable to merge

the subspace clusters C

and C

if they share certain

amount of terms and Web pages. Jaccard similarity

coefﬁcient is one of the common measure for com-

paring the similarity and diversity of the sets. The

Jaccard coefﬁcient is deﬁned as the size of the inter-

section divided by the size of the union of the sets,

Jaccard(X, Y ) =

|X∩Y |

|X∪Y |

In Algorithm 1, M erge function merges the sub-

space clusters by adopting the Jaccard coefﬁcient to

measure the similarity of the set of features and Web

pages of two clusters. If the similarity is more than the

thresholds δ and ξ respectively, we merge the clusters.

Formally, in lines 3-6 if Jaccard(f(C

), f(C

)) > δ

WEBIST 2007 - International Conference on Web Information Systems and Technologies

336

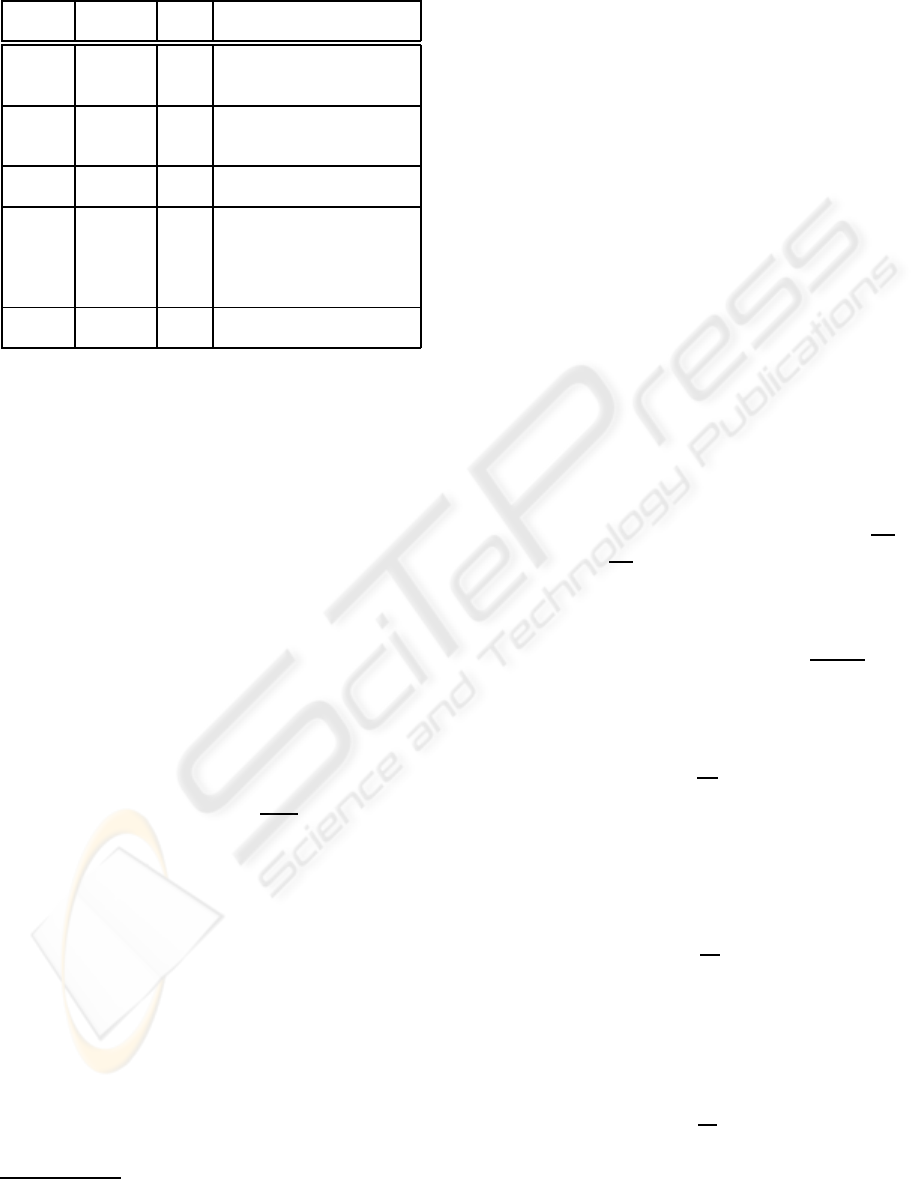
Table 1: Selected search keywords and their corresponding

categories in data sets.

Keyword # of # of Categories

categories pages

apple 6 648 Computers(463), Fruits(136),

Locations(17), Music(21),

Movies(6), Games(5)

gold 6 670 Shopping(471), Mining(151),

Movies(28), Motors(11),

Games(8), Sports(1)

jaguar 4 138 Cars(78), Video games(48),

Animals(9), Music(3)

paper 10 1422 Shopping(626), Materials(380),

Academic(113), Arts(107),

Money(78), Games(39),

Computers(27), Consultants(23),

Environment(19), Movies(10)

saturn 4 71 Cars(22), Planets(21),

Anime(19), Video games(9)

and Jaccard(w(C

), w(C

)) > ξ, the merged cluster

′

becomes C

′

= hf(C

) ∪ f (C

), w(C

) ∪ w(C

)i .

Following the same example given in Section

3.2, the two subspace clusters C

and C

is merged

due to the high overlap in their features and Web

pages. Their Jaccard coefﬁcients for the features and

Web pages are Jaccard(f(C

), f(C

)) = 0.4 and

Jaccard(w(C

), w(C

)) = 0.33.

Note that subspace clustering is a soft clustering

method that allows a Web page to be in multiple cate-

gories. This ﬂexibility is more realistic for real world

data. Besides, hard clustering is also possible. A sim-

ple idea is to assign each Web page to its closest sub-

space cluster and eliminate the duplicates from other

clusters. In the P artition function in Algorithm 1,

line 2 calculates the closest cluster for each Web page

. Here v(·) returns the feature vector. Subspace

cluster vector can be considered as the feature vector

of that cluster, and cosine measure can be used for the

similarity, similarity(x, y) =

x•y

|x||y|

where x and y

are the vectors of the cluster and the Web page.

Cosine is determined as one of the best measures

for Web page clustering, and also for binary and

sparse data (Strehl et al., 2000). Lines 4-6 remove

the duplicates from other clusters. All the remaining

Web pages which doesn’t belong to any cluster are put

in one cluster called ‘others’.

4 EXPERIMENTS

In our experiments, we identiﬁed some challenging

keywords inspired from (Zeng et al., 2004) on Open

Directory Project

(ODP).

http://www.dmoz.org

We used the search keywords ‘apple’, ‘gold’,

‘jaguar’, ‘paper’ and ‘saturn’ for data collection. For

each search keyword we prepared the data from the

resulting Web pages as givenin Table 1. In the prepro-

cessing step, the common data types of values such

as percentage, dates, numbers etc., stop words, and

punctuation symbols are ﬁltered using simple regular

expressions to standardize the data.

In each keyword data, the features are selected as

top-1000 terms which are ranked based on TF/IDF

measure as mentioned in Section 3.1. We consider

1000 terms are sufﬁciently enough to capture the con-

textual information given in the Web pages. Discus-

sions on feature selection are given in Section 4.2.

Subspace clusters are required to have at least 3

features and 3 Web pages for the thresholds α and

β. For merging subspaces, the thresholds δ and ξ are

determined as 0.2 and 0.1 respectively.

4.1 Evaluation Metrics

To evaluate the quality of our results, the clusters are

compared with the actual categories given in ODP.

We use the common evaluation metrics in cluster-

ing (Rosell et al., 2004) such as precision, recall, F-

measure, purity, and entropy. Precision, p

and recall, r

compare each cluster i with each

category j where n

is the number of Web pages ap-

pear in both the cluster i and the category j, n

and n

are the number of Web pages in the cluster i and in the

category j respectively. F-measure, F

is a

common metric calculated similarly to the one in IR.

The F-measure of a category j is F

= max

}

and similarly the overall F-measure is:

F =

. (1)

Quality of each cluster can be calculated by purity

and entropy. Purity measures how pure is the clus-

ter i by ρ

= max

}. The purity of the entire

clustering can be calculated by weighting each clus-

ter proportional to its size as:

ρ =

(2)

where n is the total number of Web pages.

The entropy of a cluster i is E

−

log p

. Calculating the weighted av-

erage over all clusters gives the entire entropy of the

clustering:

E =

. (3)

Note that for soft clustering, n in Equations 2 and

3 has to be the sum of the sizes of the clusters since

SCUBA DIVER: SUBSPACE CLUSTERING OF WEB SEARCH RESULTS

337

(a) (b) (c)

Figure 2: Comparison of clustering methods.

(a) (b) (c)

Figure 3: Effect of the future selection methods.

a Web page might appear in more than one clusters.

F-measure is related with the size of categories hence

n remains the same in Equation 1.

4.2 ODP Results

First we use a wrapper which sends the given search

keyword to http://www.dmoz.org, and collects

the resulting categories and the Web pages belong to

those categories. Collected pages are categorized by

their main ODP categories. Next, all the text is ex-

tracted from the collected Web pages.

K-means clustering method is used as a baseline

measure to demonstrate to quality of our method. K-

means is one of the common clustering methods pre-

ferred for its speed and quality. In our experiments,

even K is provided which is a great advantage for K-

means over our method. For each keyword data, K-

means has been executed 20 times and the results are

the average of all runs. Purity, entropy and F-measure

are deviated in the interval of ±0.05.

Figure 2 and Table 2 presents the performance of

the subspace clustering vs. the baseline method, K-

means. SCuBA refers to the initial subspace clusters

generated by SCuBA algorithm, Soft refers the soft

clusters after merging the subspace clusters, and Hard

refers to the ﬁnal hard clusters after partitioning.

As shown in Figure 2(a) and (b), our method sur-

passes K-means in purity and entropy measures sig-

niﬁcantly although the number of clusters are pro-

vided to K-means. SCuBA generates small but pure

subspace clusters. However, F-measure is low due to

the excessive number of clusters, and there are too

many redundant clusters with many duplicate pages

as shown in Table 3. Although sensitive and ag-

gressive merging in our method reduces the number

of clusters substantially and increases the F-measure,

there are still too many clusters and duplicates in soft

clustering, and F-measure is not comparable with K-

means. In addition, F-measure is especially low in

jaguar and saturn data since they don’t have rich

subspaces that prevents to identify common subspace

clusters to merge.

Features of some of the subspace clusters are pre-

sented in Table 4. One can notice the common terms

such as ‘contact’, ‘privacy’, and ‘see’ in paper data

that lead the worst quality among the other keywords.

Merging due to the common terms degenerates the

purity of the clusters as opposed to F-measure. An-

other reason for the purity to be low in paper data is

its context ambiguity; the context of categories have

more overlaps than the other keywords have. For in-

stance, many Web pages in Shopping, Materials, Arts,

and Money have content about the quality of papers.

Determining the number of clusters has been a

challenging problem for clustering methods. As

shown in Table 3, our algorithm generated more clus-

ters than the actual for apple and gold keywords.

Sometimes main clusters can not be generated due

to the completely separate context in subcategories.

For example, hardware and software subcategories

are identiﬁed however they are not clustered together.

Clusters are less in paper data due to the merging

caused by common terms in the data.

Top-1000 terms are sufﬁcient to include all the de-

scriptive and discriminative terms in the collections.

However, they also contain common and ambiguous

terms which hinders clustering process such as ‘e-

mail’,‘forum’, and ‘contact’.

TF, DF and TF/IDF measures have not affected

WEBIST 2007 - International Conference on Web Information Systems and Technologies

338

Table 2: Performance comparison of clustering methods. P, E and F refers to purity, entropy and F-measure respectively.

SCuBA Soft K-means Hard

Keyword P E F P E F P E F P E F

apple 0.80 0.57 0.26 0.77 0.70 0.39 0.72 1.08 0.65 0.78 0.89 0.47

gold 0.79 0.67 0.19 0.78 0.78 0.33 0.75 1.11 0.63 0.73 0.99 0.44

jaguar 0.78 0.71 0.23 0.91 0.40 0.18 0.65 1.12 0.40 0.91 0.40 0.18

paper 0.59 1.34 0.44 0.52 1.87 0.42 0.45 2.27 0.40 0.46 2.29 0.38

saturn 0.47 1.52 0.36 0.73 0.91 0.27 0.31 1.89 0.41 0.73 0.91 0.27

Table 3: Comparison of actual clusters with clustering methods. Clusters and Pages refers to number of clusters and number

of total Web pages in the clusters respectively.

# of # of SCuBA Soft K-means Hard

Keyword Cat. pages Clusters Pages Clusters Pages Clusters Clusters

apple 6 648 801 4402 181 2406 6 23

gold 6 670 578 3276 165 2077 6 27

jaguar 4 138 15 88 4 95 4 4

paper 10 1422 2054 12593 120 3516 10 6

saturn 4 71 12 86 3 66 4 3

Table 4: Sample features of one subspace cluster for each

keyword.

Keyword Sample features Related Category

apple macintosh, users, computer, Computers

product, check, imac, mac

gold necklace, ring, pendant, earring Shopping

bracelet, shipping, silver, jewelry

jaguar auto, cars, parts, support Cars

paper printing, contact, privacy, product, Shopping

unique, see

saturn planet, sun, image, satellite Planets

the performance of subspace clustering signiﬁcantly

as shown in Figure 3. Especially, TF and TF/IDF

showed nearly the same performance. As opposed

to the expectations, although the common terms are

ranked in lower, it is surprising to ﬁnd out TF/IDF is

not able to eliminate them.

Consequently, our subspace clustering based algo-

rithm preserves the quality of the clusters initially ob-

tained from SCuBA while signiﬁcantly reducing the

number of clusters. Furthermore, it is better than a

common state of art clustering algorithm although the

number of clusters are provided.

5 CONCLUSION

We present a novel subspace clustering based algo-

rithm to organize search results by simultaneously

clustering and identifying their distinguishing terms.

We present experimental results illustrating the effec-

tiveness of our algorithm by measuring purity, en-

tropy and F-measure of generated clusters based on

Open Directory Project (ODP). As the future work,

we will work on feature selection to eliminate com-

mon terms to increase the quality of the features.

Currently, merging is a simple rule based method,

whereas one can explore the use of sophisticated rela-

tionship analysis over clusters.

REFERENCES

Agarwal, N., Haque, E., Liu, H., and Parsons, L. (2006).

A subspace clustering framework for research group

collaboration. International Journal of Information

Technology and Web Engineering, 1(1):35–38.

Beil, F., Ester, M., and Xu, X. (2002). Frequent term-based

text clustering. In Proceedings of SIGKDD’02, pages

436–442, New York, NY, USA. ACM Press.

Crescenzi, V., Merialdo, P., and Missier, P. (2005). Clus-

tering web pages based on their structure. Data and

Knowledge Engineering, 54:279–299.

Leouski, A. and Croft, W. B. (1996). An evaluation of tech-

niques for clustering search results. Technical Report

IR-76, University of Massachusetts, Amherst.

Leuski, A. and Allan, J. (2000). Improving interactive re-

trieval by combining ranked lists and clustering. In

Proceedings of RIAO’2000, pages 665–681.

Parsons, L., Haque, E., and Liu, H. (2004). Subspace clus-

tering for high dimensional data: A review. SIGKDD

Explorations, 6(1):90.

Rosell, M., Kann, V., and Litton, J.-E. (2004). Compar-

ing comparisons: Document clustering evaluation us-

ing two manual classiﬁcations. In Proceedings of

ICON’04.

Strehl, A., Ghosh, J., and Mooney, R. (2000). Impact of

similarity measures on web-page clustering. In Pro-

ceedings of AAAI’00, pages 58–64. AAAI.

Zeng, H.-J., He, Q.-C., Chen, Z., Ma, W.-Y., and Ma, J.

(2004). Learning to cluster web search results. In

Proceedings of ACM SIGIR’04, pages 210–217, New

York, NY, USA. ACM Press.

SCUBA DIVER: SUBSPACE CLUSTERING OF WEB SEARCH RESULTS

339