
ESTIMATE VALIDITY REGIONS FOR NEAREST NEIGHBOR
QUERIES *
Xing Gao, Ali R. Hurson
Department of Computer Science and Engineering
Pennsylvania State University,USA
Krishna Kavi
Department of Computer Science and Engineering
University of North Texas,USA
Keywords: Location dependent query, validity region, proxy caching, nearest neighbour.
Abstract: Users’ queries for data or services in a mobile computing environment are highly relevant to their current
locations. A nearest neighbor (NN) query finds the data object closest to the user’s location; and hence, NN
query issued at different locations may lead to different results. The nearest neighbor validity region
(NNVR) is the area where an NN query result remains valid. A cached NN result can be used to answer
semantically equivalent NN queries issued in the same NNVR. Our analysis discovers that NNVRs carry
useful information about neighboring objects’ locations. This paper proposes an algorithm data mining the
hidden information in cached NNVRs to increase the proxy caching performance. The experimental results
and analysis have demonstrated the effectiveness of the proposed algorithm in reducing query response time
and workload on the database server.
1 INTRODUCTION
In a mobile computing environment, mobile users
may issue queries related to their current locations
(Barbara, 1999), e.g., “Find the nearest hospital”.
Such a query is a location dependent query (LDQ)
as its result depends on the user’s current location.
An LDQ may returns different results in different
regions. The validity region (VR) is the region
where an LDQ result remains valid.
If the user issues the same query at a new
location, the query needs to be resubmitted to the
database (DB) server. It leads to unnecessary
network traffic and DB server workload if the
mobile user is still within the VR of a previously
resolved query. The VR aware LDQ caching scheme
is one solution to address this problem. The LDQ
cache stores the most frequently (or recently) issued
LDQs, query results, and their VRs. The cache can
determine if the querying location is within the VR
of a cached result of a semantically equivalent LDQ
as defined in Gao and Hurson (2005) - some queries
can be resolved based on the cache contents.
The most common LDQ is the nearest neighbor
(NN) query, normally in the form of NN
(object_category, x, y), which retrieves the object in
the specified category that is the closest to the user’s
querying location (x, y). The nearest neighbor
validity region (NNVR) is the VR of a NN result,
and it is determined by the locations of the result
object and neighboring non-result objects (Zheng
and Lee 2001).
Because it requires the knowledge of all data
object’s locations to generate VRs, most existing
LDQ caching schemes rely on the DB server to
provide VRs for LDQ results. VR computation
introduces extra storage and processing overhead, so
the DB server may not provide VR service or
provide it only when workload permits. The
uncertainty in VR availability limits the feasibility
of those LDQ caching schemes. Alternatively, Gao
and Hurson (2005) and Gao, Sustersic, & Hurson
(2006) proposed the LDQ proxy caching scheme
* National Science Foundation under the contract IIS-0324835 in part has supported this
work.
129
Gao X., R. Hurson A. and Kavi K. (2007).
ESTIMATE VALIDITY REGIONS FOR NEAREST NEIGHBOR QUERIES.
In Proceedings of the Second International Conference on Software and Data Technologies - Volume ISDM/WsEHST/DC, pages 129-136
DOI: 10.5220/0001323801290136
Copyright
c
SciTePress

that is capable to estimate the VR based on the
observed querying events. When the DB server does
not provide the NNVRs, the proxy cache server
invokes the Right-hand algorithm proposed in Gao
and Hurson (2005) to compute the nearest neighbor
estimated validity region (NNEVR) with 3 or more
querying events known to be within the result
object’s NNVR.
Our analysis revealed that NNVRs imply
neighboring objects’ locations and their partial
NNVRs. This research identifies the value of the
hidden information and proposes an iNN_EVR
algorithm, which generates NNEVR by exploiting
both querying history and the cached content at the
proxy cache server. The experimental results will
demonstrate that iNN_EVR algorithm improves the
proxy cache performance by reducing the query
response time as well as the number of NN queries
processed by the DB server.
The rest of this paper is organized as follows.
Section 2 reviews the existing work related to LDQ
caching and NNVR estimation. Section 3 reveals the
information carried in NNVRs, proposes the
iNN_EVR algorithm, and examines the algorithm
with a running example. Section 4 presents the
simulation model and analyzes the experimental
results. Finally, section 5 concludes this paper and
outlines our future research directions.
2 RELATED WORK
The idea of queries with location constraints was
originally introduced by Imielinski and Badrinath
(1992), and has been further discussed in many other
research works such as Forman and Zahorjan
(1994), Dunham and Kumar (1998), Seydim,
Dunham, & Kumar (2001), Lee, Lee, Xu, et al
(2002). Naturally, mobile users are likely to query
data and services relevant to their current positions.
Barbara (1999) named this class of queries the
location dependent query (LDQ). Seydim, Dunham,
& Kumar (2001) distinguished LDQs from other
queries with location constraints: a query whose
result depends on certain location attributes is a
location aware query (LAQ), while a LDQ is a query
whose result depends on the mobile user’s current
location. Two common types of LDQ are NN
queries and range queries. A NN query retrieves the
data object satisfying the query that is the closest to
the querying location, while a range query retrieves
all satisfying data objects within the specific range
(Guting 1994).
Location dependent data cache also received
much research attention. Ren and Dunham (2000)
proposed a semantic caching scheme for location
dependent results, which stores the query results and
the semantic description of the queries (i.e., the
query selection relationships, selection attributes,
selection conditions, and the bound of locations).
This semantic caching scheme reduces the network
traffic and allows partial query resolution as well as
query resolution during the disconnection. Taking
validity information into the consideration, Zheng,
Xu, & Lee (2002) presented algorithms for cache
invalidation and cache replacement strategies. Hu,
Xu, Wong, et al (2005) presented a proactive
caching approach, which caches both query results
and their index in order to answer different types of
queries.
There are several algorithms for the DB server
to determine NNVRs. Zheng and Lee (2001) built
the static Voronoi diagram (VD) to partition the
search space based on the VR of each data object.
The NN query result is the object whose Voronoi
cell (VC) covers the querying location, and its VC is
the corresponding NNVR. The VD, however, is
expensive to maintain due to database updates, and
it is also inapplicable for the k nearest neighbor (k-
NN) query when k is unknown. Even when k is
known, an order-k VD is very expensive in terms of
computational and storage overhead as pointed out
by Zhang, Zhu, Papadias, et al (2003).
Consequently, Zhang, Zhu, Papadias, et al (2003)
introduced algorithms to calculate NNVRs during
the run time. It avoids the large storage overhead but
introduces extra computing and I/O cost.
In an attempt to obtain the validity region, Gao
and Hurson (2005) proposed a proxy cache scheme
associated with Right_hand algorithm to compute
NNEVRs based on the querying history observed by
the proxy server. This algorithm works for NN
query and other LDQs with convex VRs. To
generate the NNEVR for a NN result, Right_hand
algorithm searches the querying history and finds
the querying locations where the same NN query
returns the identical result. Because all these
querying locations lie in the result’s NNVR and all
NNVRs are convex polygons, Right_hand algorithm
returns the convex hull, minimum convex polygon,
of these querying locations as the NNEVR.
The works thus far discussed have overlooked
useful information in the cached NNVRs that
implies neighboring objects’ locations. Section 3
will identify the hidden information and illustrate
the approaches to improve NN caching performance.
ICSOFT 2007 - International Conference on Software and Data Technologies
130

3 GENERATING NNEVRS
This section data mines the hidden information in
cached NNVRs. A cached NNVR implies the
locations and partial NNVRs of its neighbors. Based
on this discovery, we propose the iNN_EVR
algorithm, which generates NNEVRs by exploring
both querying history and cached content. We
examine the algorithm through a working example
and analyze its characteristics and complexity.
3.1 Analysis of NNVR
The NNVR of an object is its VC formed by
perpendicular bisectors between the object and its
neighbors (Zheng and Lee 2001). An NNVR carries
valuable information about its neighbors: their
locations and two vertices in their NNVRs. Figure 1
shows a data space with 9 objects (a, b, … i) and the
surrounding polygons as their NNVRs. Take NNVR
for object e, for example, the 6 NNVR edges are the
perpendicular bisectors between object e and its 6
neighbors.
Figure 1: NN results and their validity regions.
An NNVR implies its neighbors’ locations and
their partial NNVRs. There are two types of NNVR
edges: boundary NNVR edges which lie on the data
space boundary and the non-boundary NNVR edges.
Each non-boundary NNVR edge is the
perpendicular bisector between the two neighboring
objects. Therefore, an object and a non-boundary
NNVR edge determine one neighbor’s location,
which is the object’s mirror image point across the
edge. Taking object e’s NNVR in figure 1 for
example, it implies the locations of all 6 neighbors
(b, c, d, f, h, and i).
Two neighboring NNVRs share one edge and
two vertices. The shared edge and the data object
determine a triangle, which is guaranteed to be a
sub-region of the corresponding object’s NNVR.
Figure 2 shows a client cache with NN result e and
its NNVR, illustrated by the polygon around e. It
implies its 6 neighbors’ location as well as their
partial NNVRs.
Figure 2: NN VR and its implication.
The objective of this work is to improve the
Right-hand algorithm, Gao and Hurson (2005), and
enhance the performance of LDQ caching systems.
The Right-hand algorithm requires at least three
querying locations in the same NNVR to generate an
NNEVR. We propose improved nearest neighbor
estimated validity region (iNN_EVR) algorithm that
exploits the hidden information in cached NNVRs to
generate larger NNEVRs with fewer querying
events, thus improving the performance of systems.
3.2 iNN_EVR Algorithm
Before examining the iNN_EVR algorithm
(algorithm 2 in figure 4), we first introduce the
Immediate_Neighbor algorithm (algorithm 1 in
figure 3), which determines whether the result object
shares an NNVR edge with any cached object. If
yes, this algorithm also returns two shared NNVR
vertices, which will be used to generate the NNEVR
for the result object. The iNN_EVR algorithm
generates NNEVR as the convex hull of all locations
known to be within the result object’s NNVR,
including the result object, querying locations
returning the same NN result, and the known
vertices of the result object’s NNVR.
ESTIMATE VALIDITY REGIONS FOR NEAREST NEIGHBOR QUERIES
131
Algorithm: Immediate_Neighbor (R, C
i
)
Input: R Î The Result Object (x, y)
C
i
Î Cached entry with result object O
i
Output: B Î A Boolean value
V Î Vertices
Procedure:
1. B Í False
2. For each edge E of C
i
3. If (x, y) is the image point of O
i
across E
4. B Í True // Find immediate neighbor
5. V Í Vertices of E // Find two shared NNVR
vertices
6. Exit For Loop
7. End If
8. End For
9. Return B, V
Figure 3: Algorithm 1 - Immediate_Neighbor.
Algorithm: iNN_EVR (Q, R, C, H)
Input: Q Î The Query (object_class, x, y)
R Î The Result Object (R
x
, R
y
)
C Î The Cached Results
H Î Querying History
Output: P Î NNEVR Polygon
Procedure:
1. Build an empty list L
2. Let B, V be a Boolean and a set of vertices
3. Let HR
i
be the result object of H
i
,
4. Let (HR
x
, HR
y
) be the location of HR
i
5. Let (H
x
, H
y
) be the querying location of H
i
6. For each entry C
i
in C
7. If C
i
does not have an NNVR
8. Continue
9. Else //Find NNVR vertices shared with neighbors
10. (B, V) Í Immediate_neighbor(R, C
i
)
11. If B is True //Add two vertices to list L
12. Add V to L
13. End If
14. End If
15. End For
16. If every vertex v in L appears twice
17. P Í convex hull formed by the entries in L
18. Return P //Return the accurate NNVR
19. End If
20. Add (R
x
,R
y
) to L //Result object is always in NNVR
//Find querying locations in same NNVR
21. For each entry H
i
in H
22. If Q and H
i
are semantically equivalent and
(HR
x
, HR
y
) = (R
x
,R
y
)
23. Add (H
x
, H
y
) to L
24. Else
25. Continue
26. End If
27. End For
// Generate the NNEVR
28. P Í convex hull formed by the entries in L
29. Return P
Figure 4: Algorithm 2 - iNN_EVR.
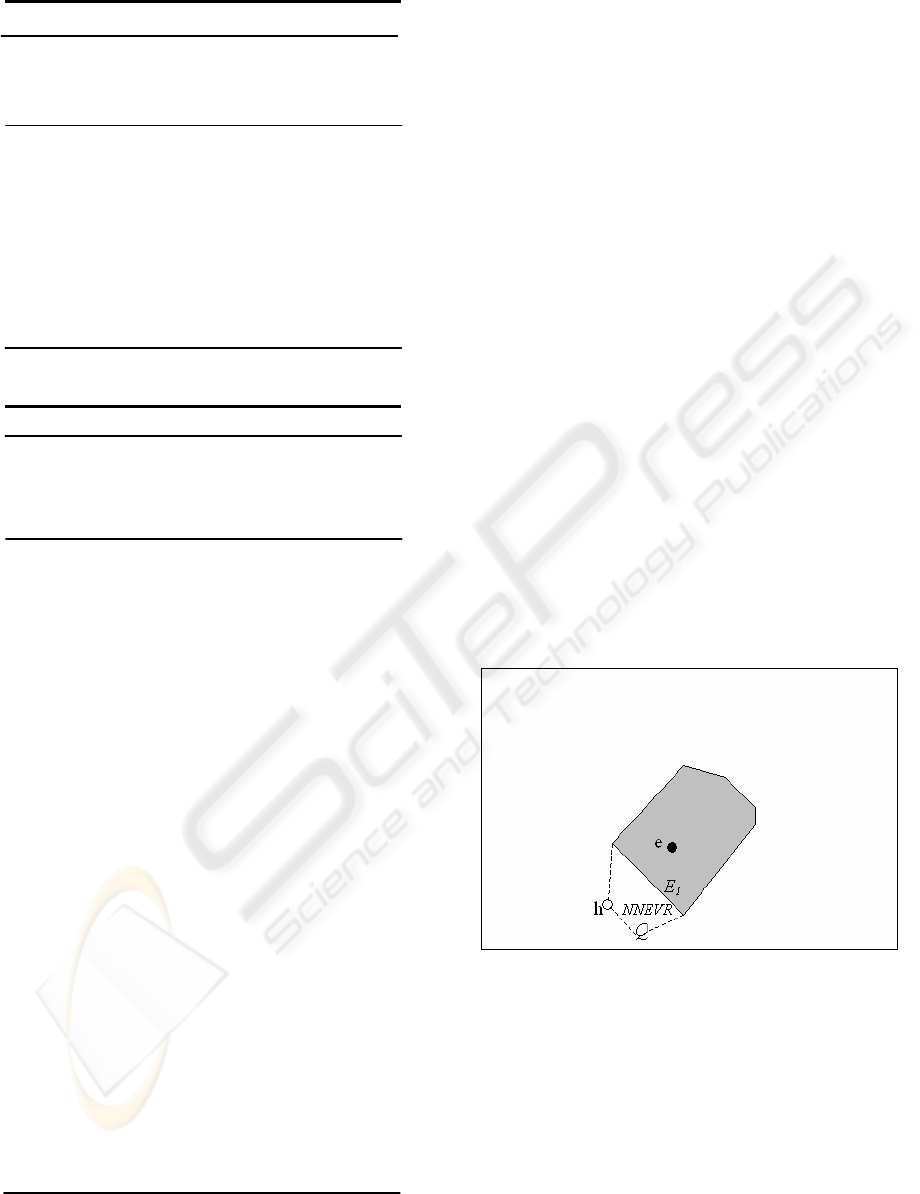
Figure 5 is a working example to examine
algorithm 2 and illustrate the generated NNEVR.
The proxy server has object e and its NNVR in its
cache when it receives an NN query issued at Q. As
Q is outside of any cached NNVRs, the proxy cache
cannot resolve the query, so it forwards the query to
the DB server, which returns the result object h
without its NNVR. The proxy cache calls on
iNN_EVR algorithm to generate NNEVR for result
object h. iNN_EVR employs Immediate_Neighbor
algorithm and finds that h and e share an NNVR
edge (E
1
). Result object h’s NNEVR is the polygon
covering h, Q, and edge E
1
. In contrast to
iNN_EVR, the original Right-hand algorithm was
not able to generate an NNEVR for query Q under
the aforementioned conditions.
The complexity of Immediate_Neighbor
(algorithm 1) to verify a cached NNVR with m
edges is O (m). The iNN_EVR algorithm consists of
searching for NNVR vertices, searching for
querying locations, and generating the convex hull.
The complexity of finding the hidden NNVR
vertices in a cache with n entries is O (m*n). The
complexity of finding the querying locations in a
querying history of h entries is O (h). After finding
p known locations in the NNVRs, the complexity of
generating the convex hull is O (p*lg p) (Graham
1972). As a result, algorithm 2 has a complexity of
O (m*n + p*lgp + h).
Figure 5: Example of the iNN_EVR algorithm.
3.3 iNN_EVR Finds NNVRs
The iNN_EVR algorithm normally returns an
NNEVR as a sub-region of the actual NNVR.
However, there is a scenario where iNN_EVR
algorithm returns the precise NNVR. Given a new
result object, if all of its immediate neighbors and
their NNVRs are in the cache, the shared NNVR
vertices form the NNVR of the result object. Figure
6 illustrates this scenario in which objects b, i, d, f,
ICSOFT 2007 - International Conference on Software and Data Technologies
132

h, i, and their NNVRs (the gray polygons covering
different objects) are cached. An NN query is issued
at location Q, whose result is not cached. The proxy
server forwards the query to the DB server which
returns result e without its NNVR. To determine e’s
NNEVR, iNN_EVR algorithm discovers that all
vertices are shared by two cached NNVRs, which
indicates that these shared vertices form the accurate
NNVR for result object e.
Figure 6: iNN_EVR finds an accurate NNVR.
The iNN_EVR algorithm has several
advantages over the existing Right_hand algorithm.
First, it exploits the hidden information in cached
NNVRs and obtains NNEVRs with fewer querying
events. Second, it can calculate the actual NNVR of
a result object under special circumstances. Given a
new result object, if all of its immediate neighbors
and their NNVRs are stored in the cache, the shared
NNVR edges form the NNVR for the result object.
Finally, the NNEVRs generated by iNN_EVR
algorithm are relatively larger than those generated
by the Right-hand algorithm. Section 4 presents the
experimental results and shows the performance
improvement obtained by iNN_EVR algorithm with
respect to the query response time and the number of
NN queries processed by the DB server.
4 SIMULATIONS AND
EVALUATIONS
4.1 Simulation Model
We evaluated the performance improvement of the
iNN_EVR algorithm over the Right-hand algorithm
using a proxy caching simulator in CSIM (CSim).
For a fair comparative analysis, we ran three
configurations with similar environmental setup as
that used by Gao, Sustersic, & Hurson (2006). The
first configuration, named “iNN”, employs
iNN_EVR algorithm. The second configuration,
named “RH”, is equipped with the Right-hand
algorithm, Gao and Hurson (2005), to generate
NNEVR. The third configuration, named “NO”,
does not use any EVR algorithm.
The simulator in Gao, Sustersic, & Hurson
(2006) modeled a mid-size town, considering the
demographic information. It partitioned the
simulated area into different regions to reflect the
population density during and outside of working
hours. Mobile users are categorized into different
groups each with different mobility patterns. As
listed in table 1, our simulator uses the same
parameters as Gao, Sustersic, & Hurson (2006) for
DB servers, proxy server cache, client cache, and
network traffic.
Table 1: Major simulation parameters.
Parameters Value
Number of data objects about this city 680
Proxy cache size (NN result entries) 100
Client cache size (NN result entries) 10
Proxy querying history size 500
Network bandwidth, base station (BS) to
DB link (Mbps)
1000
Background network (BS to DB)
utilization
0.4
Client to BS link bandwidth (Kbps) 19.2
BS to client link bandwidth (Kbps) 144
NN query request size (byte) 32
Average NN query result size (byte) 80
Average NNVR descriptor size (byte) 60
Average query rate, daytime (hours) 0.5
Average query rate, night (hours) 0.2
The performance improvement is measured by
two metrics: the relative speedup of NN query
response time and the relative DB server workload
reduction. The DB server workload reduction can be
approximated by the number of queries sent to DB
servers.
NQDB
RH
is the number of NN queries sent to
the DB servers in RH configuration, and NQDB
iNN
represent the number of NN queries sent to the DB
server in iNN configuration. The DB server
workload reduction (R
workload
) is the difference
between NQDB
RH
and NQDB
iNN
divided by
NQDB
RH
(see equation 1). The average query
response time for a RH configuration is termed as
RT
RH
. RT
iNN
represents the average query response
time in iNN configuration. The speedup of NN
query response time (S
response
) is the difference
between RT
RH
and RT
iNN
divided by RT
RH
(see
equation 2).
ESTIMATE VALIDITY REGIONS FOR NEAREST NEIGHBOR QUERIES
133

R
workload
=
RH
iNNRH
NQDB
NQDB - NQDB
(Eq. 1)
S
response
=
RH
iNNRH
RT
RTRT −
(Eq. 2)
4.2 Evaluations and Analysis
We simulated and compared the performance of
Right-hand and iNN_EVR algorithms under
different scenarios in which the DB server provides
NNVRs with probabilities (0%, 20%, 40%, 60%,
80%, and 100%). Figures 7 and 9 show percentage
of NN queries sent to the DB server and the average
query response time for the aforementioned
configurations, respectively. Figure 8 and 10 depict
the relative workload reduction and relative speed
up of query response time, achieved by iNN
configuration over RH configuration as formulated
in equation 1 and 2.
The NNEVRs in RH and iNN configurations
help to resolve more NN queries at proxy cache
server and thus reduce the query traffic sent to DB
servers. From figure 7, one can conclude that both
RH and iNN configurations significantly reduce the
workload sent to the DB server, especially when
NNVR availability is low. In the scenario where DB
servers do not provide NNVR services, the proxy
caching scheme in NO configuration can only
answer queries issued at the same location as a
cached result. As a result, many NN queries are
forwarded to DB servers. The iNN configuration
employs iNN_EVR algorithm and generates larger
NNEVR than those generated by Right_hand
algorithm (in RH configuration), which explains the
fact that iNN outperforms RH in reducing the
number of NN queries sent to DB servers.
Figure 8 illustrates the improvement achieved
by iNN_EVR algorithm over Right-hand algorithm
with respect to the workload at the DB server. In the
case that the DB server always provides NNVRs,
both algorithms lead to the same performance. When
the DB server never provides NNVRs, iNN_EVR
algorithm achieves a relative workload reduction of
12% over Right-hand algorithm.
20
40
60
80
100
0 20406080100
VR availability (%)
Queries sent to DB servers (%)
iNN
RH
NO
Figure 7: Number of queries sent to DB servers.
0%
2%
4%
6%
8%
10%
12%
0 20406080100
VR availability (%)
Relative workload reduction
Figure 8: Workload reduction at DB servers.
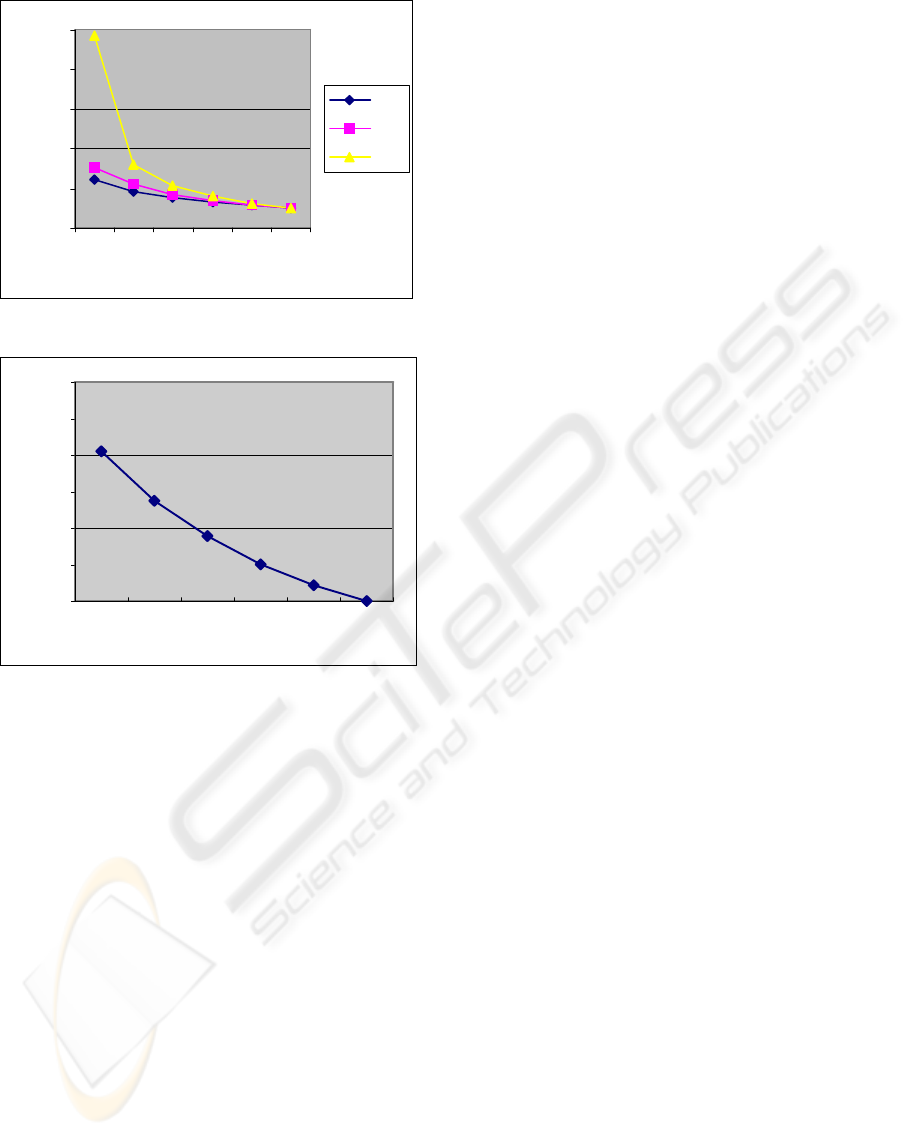
Figures 9 show the average query response time
observed in three configurations. The NNEVRs
generated in RH and iNN configurations help to
resolve some NN queries using proxy cache and
thus reducing query response time. The fewer NN
queries sent to the DB server, the shorter NN query
response time. Due to this relationship, figure 9
shows the average query response time for the three
aforementioned configurations, which shows a
similar pattern as the curves in figure 7. Both RH
and iNN reduces the query response time and the
improvement is significant when NNVR availability
is low. iNN configuration leads to a shorter query
response time than RH configuration because iNN
resolves more queries at proxy server. Figure 10
illustrates iNN_EVR algorithm’s relative speedup
over Right-hand algorithm with respect to the
response time as formulated in equation 2. When
NNVR is always available, three configurations
behave in the same way, as there is no need to
generate NNEVRs. The relative response time speed
up is 8% when the DB server does not provide VR
services.
ICSOFT 2007 - International Conference on Software and Data Technologies
134
0.02
0.03
0.04
0.05
0.06
0.07
0 20406080100
VR availability (%)
Query response time (s)
iNN
RH
NO
Figure 9: NN query response time.
0%
2%
4%
6%
8%
10%
12%
0 20406080100
VR availability (%)
Speed up of response time
Figure 10: Speed up in LDQ response time.
5 CONCLUSIONS AND FUTURE
WORK
Our analysis revealed that the cached NNVRs can be
data mined to exploit valuable information on their
neighbors’ locations and NNEVRs. We proposed an
algorithm to generate NNEVRs by exploring both
the querying history and the cached content. This
algorithm was evaluated using a detailed simulation
scenario modeled after a real, modern community
and including components that consider actual
population demographics and data objects. The
simulation results showed that the iNN_EVR
algorithm achieved better performance than the
existing algorithm.
The hidden information in cached NNVRs can
help disconnected mobile users to answer queries
issued in proximity of cached NNVRs. Our future
research will seek schemes to resolve more queries
for disconnected users. In addition, we will study the
location-based services with respect to users’
mobility patterns based on the road network.
Furthermore, some mobile users prefer fast response
time and tolerate certain level of inaccuracy on LDQ
results or their VRs. We will study Quality of
Service (QoS) issues in LDQ cache management to
further improve the system performance.
REFERENCES
Barbara, D., 1999. "Mobile Computing and Databases - A
Survey", IEEE Transactions on Knowledge and Data
Engineering, 11(1), pages 108-117.
CSIM product website. http://www.mesquite.com/
Dunham, M., Kumar, V., 1998. "Location Dependent Data
and its Management in Mobile Databases",
Proceedings of the Ninth International Workshop on
Database and Expert Systems Applications, pages
414-419.
Forman G., Zahorjan J., 1994. "The Challenges of Mobile
Computing", IEEE Computer, Volume: 27(4), pages
38-47.
Gao X., Hurson A., 2005. "Location Dependent Query
Proxy", ACM Symposium on Applied Computing,
pages 1020-1024.
Graham, R., 1972. “An Efficient Algorithm for
Determining the Convex Hull of a Finite Planar Set",
Information Processing Letter, 1: 132-133.
Gao X., Sustersic J., and Hurson A., 2006. "Window
Query Processing with Adaptive Proxy Cache",
Mobile Data Management (MDM), p. 39.
Guting R., 1994. "An Introduction to Spatial Database
Systems", Special Issue on Spatial Database Systems
of the VLDB Journal, 3(4), pages 357-399.
Hu H., Xu J., Wong W., Zheng B., Lee D., and Lee W.,
2005. "Proactive Caching for Spatial Queries in
Mobile Environments", IEEE International
Conference on Data Engineering, pages 403-414.
T. Imielinski and B. Badrinath, 1992. "Querying in Highly
Mobile Distributed Environments", International
Conference on Very Large Data Bases (VLDB), pages
41-52.
Lee D., Lee W., Xu J., and Zheng B., 2002. "Data
Management in Location-Dependent Information
Services: Challenges and Issues", IEEE Pervasive
Computing, 1:3, pages 65-72.
Ren Q. and Dunham M., 2000. "Using Semantic Caching
to Manage Location Dependent Data in Mobile
Computing", International Conference on Mobile
Computing and Networking, pages 210-221.
Seydim A., Dunham M., and Kumar V., 2001. "Location
Dependent Query Processing", International
Workshop on Data Engineering for Wireless and
Mobile Access, pages 47-53.
Zheng B. and Lee D., 2001. "Semantic Caching in
Location-dependent Query Processing", Seventh
International Symposium on Spatial and Temporal
Databases, pages 97-116.
ESTIMATE VALIDITY REGIONS FOR NEAREST NEIGHBOR QUERIES
135

Zheng B., Xu J., and Lee D., 2002. "Cache Invalidation
and Replacement Strategies for Location-Dependent
Data in Mobile Environments", IEEE Trans. on
Computers, Special Issue on Database Management
and Mobile Computing, 51(10), pages 1141-1153.
Zhang J., Zhu M., Papadias D., Tao Y., and Lee D., 2003.
"Location-based Spatial Queries", International
Conference on Management of Data (SIGMOD),
pages 443-453.
ICSOFT 2007 - International Conference on Software and Data Technologies
136
