
ANALYSIS OF ONTOLOGICAL INSTANCES
A Data Warehouse for the Semantic Web
Roxana Danger and Rafael Berlanga
Department of Informatics Languages and Systems, Universitat Jaume I
Keywords:
Semantic Web, Data Warehouse, Description Logic.
Abstract:
New data warehouse tools for Semantic Web are becoming more and more necessary. The present paper
formalizes one such a tool considering, on the one hand, the semantics and theorical foundations of Description
Logic and, on the other hand, the current developments of information data generalization. The presented
model is constituted by dimensions and multidimensional schemata and spaces. An algorithm to retrieve
interesting spaces according to the data distribution is also proposed. Some ideas from Data Mining techniques
are incorporated in order to allow users to discover knowledge from the Semantic Web.
1 TOWARD PATTERN
RECOGNITION IN THE
SEMANTIC WEB
The Semantic Web is a new form of web conceived
for allowing human users and software tools to pro-
cess and share the same sources of information. The
Semantic Web relies on a set of standards which pro-
vide syntactic consistency and semantic value to all
of its content. For example, Description Logic is used
as the theoretic base for the description of web items,
and the languages RDF and OWL for their syntac-
tic representation. Description Logic defines a family
of knowledge representation languages which can be
used to represent, in a well-understood formal way,
the knowledge of an application domain. This knowl-
edge, known as ontology, ranges over the termino-
logical cognition of the domain (the interesting object
classes, or concepts, its Tbox) and its examples (the
instances of the object classes, its Abox).
Data analysis in the Semantic Web will be the
most important process when the population of on-
tologies
1
becomes a reality. Its final goal is the recog-
nition of patterns amongst the values of the attributes
1
The population of ontologies is the process of adding
instances to an ontology in order to enrich it with examples
of its domain knowledge.
of the ontological instances, which could turn into
knowledge or allow its discovery. OWL tools allow
users to create new concepts related to one or more
existing ontologies, and to determine the instances as-
sociated to such concepts.
An additional tool is needed if we want to perform
in a versatile way customized data analysis, either full
or partial, so that each object can be studied from dif-
ferent points of view focusing on distinct particular
features. Such a tool should allow users to navigate
through an instance set and its properties, being able
to discriminate between relevant and superfluous in-
formation. Moreover, it should compute and display
statistical indexes able to describe and report about
the extracted patterns.
The formalization of such a tool, following the
framework described below, is the purpose of the
present work. Starting from an available ontology,
this is enriched with information provided by the data
analyst, for example specifying the atomic data com-
bination functions. These functions provide the way
for combining atomic data to form a generalized in-
stance representing a set of instances. Then, two main
structures have to be built: the conceptual dimensions
and the multidimensional conceptual spaces. The
conceptual dimensions are partial order specifications
between objects, which allow to browse through their
semantic relations. The multidimensional conceptual
13
Danger R. and Berlanga R. (2007).
ANALYSIS OF ONTOLOGICAL INSTANCES - A Data Warehouse for the Semantic Web.
In Proceedings of the Second International Conference on Software and Data Technologies - Volume ISDM/WsEHST/DC, pages 13-20
DOI: 10.5220/0001332200130020
Copyright
c
SciTePress

spaces can be seen as “intelligent object containers”.
They make use of a subset of conceptual dimensions,
a specification of relevant abstraction levels and a
set of atomic data combination functions in order to
(re)construct appropriate generalized instances. Dif-
ferent statistical indexes (e.g. frequencies), associated
to the conceptual dimensions, can be used to char-
acterize patterns in the conceptual spaces. The most
suitable data analysis technique for carrying out this
proposal is data warehousing.
The present work is not the first attempt to formal-
ize a data warehouse for the Semantic Web. Within
the Data Warehouse Quality (DWQ) project (Hacid
and Sattler, 1998) a formalization for the multidimen-
sional modeling based on an extension of the con-
structors of description logic is proposed. In this way,
new object classes could be described by specify-
ing aggregability operations, and the traditional rea-
soning over ontological instances could be applied.
However, the demonstration of the undecidability of
minimal languages that operate with aggregate opera-
tors(Baader and Sattler, 2003) makes the proposal of
the DWQ project unfeasible.
On the other hand, the ideas of the traditional data
warehouse (and OLAP techniques) has been extended
to object oriented modeling, (Buzydlowski et al.,
1998; Trujillo et al., 2001; Nguyen et al., 2000; Binh
and Tjoa, 2001; Abell
´
o, 2002). Considering that de-
scription logic was designed as an extension to frames
and semantic networks, the basis of object-oriented
data warehouse could be applied in order to define
a data warehouse for the Semantic Web. However,
the flexibility of object-oriented formalization causes
a more sparse structure in object-oriented databases
that in traditional ones. Moreover, the restrictions of
OLAP implementations drastically reduce the useful
set of objects to be used in the analysis.
Unlike these previous works, this paper proposes
a multidimensional model for the analysis of ontolog-
ical instances that merge both approaches. The idea
is the creation of meta-ontologies in order to enrich
the knowledge of ontologies with data analysis infor-
mation. This data analysis information focuses on the
description of interesting object classes and on the ag-
gregation process. The reasoning of description logic
is used in a preliminary phase to 1) recover the satisfi-
able
2
object classes that can be used on analysis pro-
cesses, 2) discover the hierarchical and aggregate or-
ders between the classes, and 3) assign each instance
to the set of object classes to which it belongs.
This paper describe our proposal in detail. Firstly,
2
A concept (or object class) is satisfiable if it is consis-
tent and there exists an interpretation on which appears at
least an instance of this concept.
the data analysis information is introduced. Then, the
proposed model is described, starting from the defini-
tion of dimensions and their operators (section 3) and
following with the specification of the multidimen-
sional conceptual space (section 4). The two follow-
ing sections are focused on the extraction of interest-
ing conceptual spaces and their use, respectively. The
last section gives some conclusions and future work.
2 ANALYSIS METADATA
Information descriptions useful for the analysis are
those available in the ontologies in form of instances.
However, they are not enough to analyze data and dis-
cover patterns. New interesting concepts and partic-
ular issues related to the generalization process are
essential in order to generate descriptions that repre-
sent relevant and realistic visions of the application
domains of the analyzed ontologies. We call all this
information analysis metadata, which comprises the
following elements:
• description of new concepts, which it is used to in-
troduce additional levels of abstraction in the con-
cept hierarchies expressed in an ontology, and/or
to link concepts from different ontologies. New
concepts may be obtained extending old ones with
paths to previously unrelated concepts. They can
also semantically represent hierarchical clusters
obtained using clustering algorithms.
• description of the combination functions (see def-
inition below); it is used to specify ways for gen-
eralizing sets of data of the same type during the
instance generalization process. The data analyst
is responsible for deciding the combination func-
tions that are semantically suitable for a given data
set. For example, the combination function which
computes the average of a set of values is seman-
tically suitable for a temporal sequence of temper-
atures of a town, but not for a set of temperatures
of different towns.
Although it is perfectly plausible to define such
descriptions for every new multidimensional concep-
tual space, a better solution is to keep this semantic
information always available and to apply it accord-
ing to the requirements of each case. This goal can be
achieved building a meta-ontology containing the sort
of information described above, again using Descrip-
tion Logic. In this way, analysts can proceed more ef-
ficiently as they can reuse the analysis metadata. Even
more importantly, in this way the coherence of differ-
ent studies is granted, providing an ontology with an
intrinsic robustness toward analysis processes. Thus,
ICSOFT 2007 - International Conference on Software and Data Technologies
14

further studies can be more easily performed by com-
paring different analysis on the same knowledge do-
main and/or the point of views of different analysts.
The description of the combination functions can
be specified through instances associated to the notion
of Combinable Concept of this meta-ontology:
CombinableConcept ≡
≡ ∃hasConcept.URI ⊓ ∀hasRelation.URI⊓
∃hasCombinationFunction.CombinationFunction
CombinationFunction ⊑
⊑ ∃hasName.String⊓ ∃hasImplementation.URI
Combinable concepts are those for which a com-
bination function can be defined. A combinable con-
cept can be a datatype, a named concept (defined via
a URI), or a concept derived from a composition of
relations beginning with a named concept (specified
by the URI where the start concept is defined and the
relations from it).
3 DIMENSIONS AND THEIR
OPERATIONS
A dimension is described by a set of concepts and the
way to browse through them. Such browsing is per-
formed using the operators of abstraction and general-
ization between ontological instances, and the selec-
tion operators defined below.
We consider that an abstract ontology is consti-
tuted only by the terminological knowledge. An on-
tology that contains a set of instance axioms (the Abox
of the ontology, composed by axioms specifying the
class C of an instance a -C(a)- or the relations be-
tween two instances a and b -R(a,b)-) is called con-
crete ontology. As it is usual in description logic, the
interpretation of the ontology is (I = ∆
I
,.
I
), where ∆
I
denotes the set of instances belonging to an ontology
O , and .
I
the interpretation of the concepts defined on
O ; I x represents that x is deduced from I; ⊤ rep-
resents the top concept: thing. We denote with
A the
Abox of
O , with R the set of axioms associated with
the relations of an ontology, with N
C
and N
R
the set
of named concepts and relations of the ontology, re-
spectively. Besides, the interpretation of a datatype is
defined by I
D
= (Φ
D
,.
D
), where Φ
D
denotes the data
set belonging to a datatype, Φ, of the ontology, and
.
D
associates each datatype Φ with a strict subset of
data in Φ
D
, ∆
I
∩Φ
D
=
/
0. All representable data in the
ontology belongs to the set
U = ·
I
∪ ⊕
D
.
The definition of path between two concepts C
and C
′
and that of dimensional partial order are given
below. Intuitively, the former is the set of lists of
relation-concept pairs that links C and C
′
by using
consistent ontological definitions, and the latter is
used to relate concepts using both the aggregate (as
defined bellow) and the hierarchical order between
concepts implicitly defined in a given ontology
O .
Definition 1. Path(C,C
′
) = ⊕
1≤i≤n
h
RS
i
,C
i
i
is an ag-
gregation path from concept C to concept C
′
of the
ontology
O if C
1
= C, C
n
= C
′
, and there exists an in-
terpretation I = (∆
I
,.
I
) of
O such that ∃x
i
∈ ∆
I
,0 ≤
i ≤ n, such that x
0
∈ C
I
y x
i
∈ C
I
i
,
h
x
i−1
,x
i
i
∈ R
I
i
, for
1 ≤ i ≤ n, R
i
∈ RS
i
.
The process of path retrieval must be exhaustive
enough to allow the recovering of all aggregation re-
lations between two concepts. It can be performed
by using an extension of the tableau algorithm for the
SHOIQ(D) language (Danger, 2007). It is worth em-
phasizing that these paths not only describe the aggre-
gation relations between two concepts, but also the
aggregation order between all concepts of an ontol-
ogy.
Definition 2. Let
O be an ontology. A dimensional
partial order, denoted as
⊏
→ is a partial order between
all possible pairs of concepts C,C
′
∈ N
C
defined ac-
cording to the following constraints:
• C
⊏
→ C
′
if C
′
⊏ C, or
• C
⊏
→ C
′
if ∃Path(C,C
′
)
The symbol
⊏
→ ∗ is the reflexive and transitive closure
for relation
⊏
→.
Definition 3. Let
O be an ontology. The pair D =
(C
d
,
⊏
→) is a conceptual dimension, being C
d
a set of
satisfiable concepts in
O , ⊤ ∈ C
d
and
⊏
→ the relation
of dimensional partial order for the elements in C
d
.
Example 1. In Figure 1 a workplace dimension
which combines hierarchical and aggregation rela-
tions is shown. This dimension can be used to identify
a specific place with different levels of granularity.
Workplace
Sector
Stratigraphic
Unit
Archaeological
Site
Municipality
Country
Continent
Figure 1: Workplace. dimension.
Operations
The ontological instances of each dimension can
be represented by using different point of views of
ANALYSIS OF ONTOLOGICAL INSTANCES - A Data Warehouse for the Semantic Web
15

(concepts associated with) the dimension. It is thus
necessary to define two different kinds of operations
over such instances. The first one is the selection op-
erator, used to specify the interest portion of the in-
stance that must be shown (for example, when the
concept represented by a dimension is replaced by a
concept related to the first one by an aggregate re-
lation). The second important operation is the gen-
eralization, used to generalize a set of instances (for
example, when the concept represented by a dimen-
sion is replaced by a concept related with the first one
by a hierarchical relation). The following definitions
formalize these operators.
Definition 4. Let
O be a concrete ontology with Abox
A ; the description of an instance a ∈ A is the set
d(a) = {R(a,b), R(a,b) ∈
A }. This instance is said
to be of type C if C is the most specific concept that
can be deducted from I for a, i.e., ∀C∗ such that
I C ∗ (a), C ⊏ C∗.
Definition 5. Instance a
′
is called the specialization
of an instance a of class C towards class C
′
, if its de-
scription d(a ↑
C
′
a
′
) is not undefined, and if
A \C(a) ∪
{C
′
(a
′
),d(a)}∪d(a ↑
C
′
a
′
) is consistent. The descrip-
tion of d(a ↑
C
′
a
′
), is defined as follows:
{R
′
(a
′
,b
′
)|R(a,b) ∈ d(a),
fe(C,C
′
)(R) = {
h
R
′
,C
′
i
},
d(b ↑
C
′′
b
′
) 6= unde fined},
if ∃ f
e
(C,C
′
),
|
d(a ↑
C
′
a
′
)
|
=
|
d(a)
|
unde fined, otherwise
where f
e
is a specialization function of the con-
cept C to the conceptC
′
. This function defines how to
transform each relation on the abstract concept to the
appropriate relation on the specialized concept (Dan-
ger, 2007).
The operation of abstraction of an instance, de-
noted by d(a ↓
C
′
a
′
), can be defined in a similar way.
Definition 6. Let
O be an ontology. Let ℓ be an un-
defined data that represent any data in
U . A pseudo-
instance a
3
of type C is a selector if its description,
d(a), satisfies that:
∀b
|
∃{R
1
,...,R
n
} ⊆ N
R
,R
1
(a,a
1
),...,R
n−1
(a
n−1
,a
n
),
R
n
(a
n
,b) ∈ d(a) ⇒
b ∈ {ℓ}
∀C
′
,∃Path(C,C
′
)and R
1
,..., R
n
is the order of the relations on Path(C,C
′
)
C
′I
.
Definition 7. Let
O be a concrete ontology with Abox
A , a ∈ U . Let ℓ be an undefined data that represent
any data in
U . An instance a
′
∈ U is selected by an
instance selector a if:
3
We call a pseudo-instance because ℓ does not belong to
the ontology, although in order to improve the clarity of the
explanation we will call it instance selector.
• a
′
∈ Φ, a
′
∈ {a,ℓ} or
• a ∈ C
I
,C ∈ N
C
y a
′′
computed for d(a
′
↓
C
I
a
′′
) is
such that:
∀b ∈ Φ∪ {ℓ} such that ∃R
1
(a,a
1
),...,
R
n−1
(a
n−1
,a
n
),R
n
(a
n
,b) ∈ d(a) ⇒
∃R
1
(a
′′
,a
′′
1
),...,R
n−1
(a
′′
n−1
,a
′′
n
),R
n
(a
′′
n
,b
′′
) ∈
∈ d(a
′′
) ∧ (b
′′
= b∨ b = ℓ)
Example 2. In Figure 2 a fragment of an arche-
ology ontology is represented. A selector in-
stance a constituted by the set {has
morphology(a, a’),
has
group(a’, “open”), has order(a’, ℓ), has decoration(a,
ℓ), has
color(a, “gray”) } allows the users to recover
from the ontology the descriptive fragments of ce-
ramic artifacts instances according to the properties
group, order, decoration and color, but notice that the
morphologic group of the ceramic must be open, and
its color gray.
Definition 8. Let c
Φ
D
be a function (called a com-
bination of simple data) which allows each datatype
Φ to be mapped to another function rep
Φ
, which in
turn maps subsets of Φ in a compact representation
of the input subset
4
. Let d, d
′
be two data in ∆
I
∪ Φ
D
.
A complete combination of data d and d
′
is the data
d
·
∪
t
d
′
computed as follows:
c
Φ
D
(Φ)({d, d
′
}), if {d, d
′
} ⊆ Φ,
d
′
·
∪
t
d,
if d ∈
∗
C, d
′
∈
∗
C
′
,
C ⊑ C
′
d(d ↑
C
′
d
′
) ∪ d(d
′
)\
\{R(d
′
,b
1
),...,R(d
′
,b
n
)|
{b
1
,...,b
n
} ⊆
∗
C
′′
}∪
∪{R(d
′
,b
1
·
∪
t
...
·
∪
t
b
n
)|
{R(d
′
,b
1
),...,R(d
′
,b
n
)|
{b
1
,...,b
n
} ⊆
∗
C
′′
}
if d ∈
∗
C, d
′
∈
∗
C
′
,
C
′
⊑ C and
during the process
no indefinitions
are obtained
unde fined,
otherwise
In particular, two types of functions for data com-
bination can be identified:
• unification functions which map data from 2
Φ
to
Φ. They can be oriented to statistical indexes,
such as means or deviations. Of special interest
is the function restrictive unification defined for
all types of data as:
f({d
1
,...,d
n
}) =
d, if d
1
= ... = d
n
unde fined, otherwise
4
For example, if Φ
D
= {Z }, c
Φ
D
=
{
h
Z , rangeOfIntegerSets
i
}, where the function
rangeOfIntegerSets has domain Z and as images the most
compact representations of integer sets, 2
Z
, using integer
range sets, then rangeOfIntegerSets({1,2, 3, 4,5, 7}) =
[1,5] ∪ [7, 7].
ICSOFT 2007 - International Conference on Software and Data Technologies
16
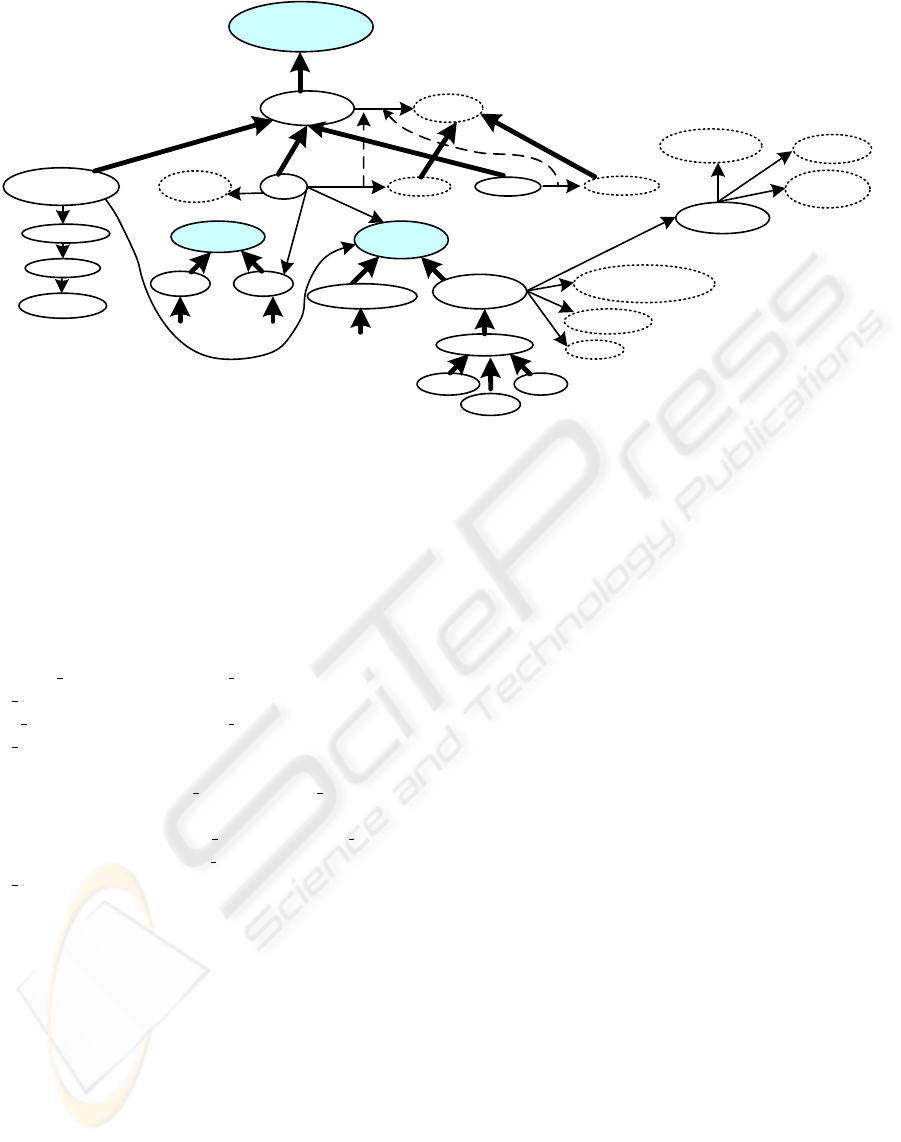
Archaeological
Site
Municipality
Country
Archaeological
Context
Workplace
SU
Artifact
Id_Wp
Id_SU
Stone Artifacts
Morphology
Ceramic Part
Body
Neck
Base
ovoid, cylinder,
cone, ...
open,
closed
deep, flat
gray, ochre,
Black,...
weight
Excavation
date
Period
Interpretation
Culture
…
…
…
Ceramic
Artifacts
Id_Sector
Sector
Continent
polished, stamping,
incision,...
Figure 2: Fragment of an archeology ontology. The concepts are represented in ellipses, the shady ones correspond to root
concepts of different hierarchies of the ontology and the dashed-line ones correspond to datatypes. The thick lines represent
the hierarchical relations between concepts, the thin lines aggregation relations and the dashed lines represent hierarchies
between relations.
• generalization functions: which map data from 2
Φ
to a compact notation.
Example 3. Let d be an instance represented by the
set {has
color(a, “black”), has decoration(“incisions”),
has
weight(20g)} and d
′
an instance represented by
{has
color(a, “ochre red”), has decoration(“incisions”),
has
weight(12g)}. The outcome of the combination
of d and d
′
by using the union of sets as combina-
tion function for the has
color and has decoration
relations and the maximum of values as com-
bination function for has weight is {has color(a,
{“black”, “ochre red”}), has
decoration({“incisions”}),
has
weight(20g)}. However, if all relations have to be
combined using unification functions, the result is un-
defined, because d and d
′
have different values for the
same relations.
4 MULTIDIMENSIONAL
CONCEPTUAL SPACES
The definitions of multidimensional conceptual
schema and multidimensional conceptual space are
given below. The former can be seen as the structure
which defines how to analyze the information. The
latter is the container where the analyzed instances
are described according to the specifications of the
schema.
Definition 9. Let
O be an ontology, C ∈ N
C
and
CC = path
1
,..., path
n
a set of paths from concept C
toward concepts C
∗
1
,...,C
∗
n
, respectively, (i.e., path
i
=
⊕
1≤ j≤n
i−1
D
RS
i
j
,C
∗
i
j
E
⊕
D
R
i
n
i
,C
∗
n
E
). The tuple E =
(D
1
,...,D
n
,c
φ
1
,...,c
φ
n
) is an n-dimensional (or sim-
ply multidimensional) conceptual schema of
O as-
sociated to C using paths CC, where it is satisfied
that∀D
i
= (Cd
i
,
⊏
→), ∀C
i
j
∈ Cd
i
, C
∗
i
⊏
→ ∗C
i
j
and c
φ
i
is a function which assigns a combination function to
each simple type of data that can be reached from a
concept in Cd
i
.
Definition 10. Let
O be a concrete ontology with
Abox
A . Let E be an m-dimensional conceptual
schema of
O associated to C using the paths in CC.
The set of tuples {t
1
,...,t
n
}, t
i
= (d
i
1
,...,d
i
m
), t
i
6=
t
j
,∀i, j ∈ {1,..., n} is called m-dimensional concep-
tual space of
O with respect to E, if for each data:
1. d
i
k
∈ C
I
i
s
,C
i
s
∈ Cd
i
, or
2. ∃d ∈ C
I
i
s
such that d
i
k
is an instance selected with
respect to a selector instance of class C
i
s
, or
3. d
i
k
is a generalized data of a dataset selected with
respect to a selector instance of class C
i
s
,C
i
s
∈
Cd
i
.
Each t
i
represents a generalized instance of a set of
instances of A selected with respect to a selector in-
stance of class C which contains all paths in CC.
ANALYSIS OF ONTOLOGICAL INSTANCES - A Data Warehouse for the Semantic Web
17

Table 1: Analysis and generalization of ceramic artifacts.
Each row maintains the number of instances represented by
the associated description (values between parenthesis).
Decoration Morphology Weight [g]
incisions
group:{open}
order:{ovoid, spheroid} 20 (3)
polished
group:{open, closed}
order:{cone, ovoid} 500 (3)
stamping
group:{open}
order:{cone} 5 (2)
without dec.
group:{closed}
order:{spheroid} 12 (2)
Example 4. The multidimensional schema shown
in Table 1 has been constructed by using the
following multidimensional conceptual space as-
sociated to the concept CeramicArtif act, E =
(D
1
,D
2
,D
3
,c
φ
union
,c
φ
union
,c
φ
max
), where:
D
1
= ({Decoration},
/
0),
D
2
= ({Morphology},
/
0),
D
3
= ({Weight},
/
0),
c
φ
union
= {
h
Φ,
ˆ
∪
i
|Φ ∈ Φ
D
},
c
φ
max
= {
h
ℜ,Max
i
}.
ˆ
∪ is defined by
ˆ
∪(d
1
,...,d
n
) = {d
1
} ∪ ... ∪ {d
n
} and
Max represent the maximum function for real num-
bers (in this case to compute the maximum weight in
each generalization).
Algorithm for the generation of multidimensional
conceptual spaces
Algorithm 1 describes how an m-dimensional
conceptual space is obtained from a given ontology
O and a conceptual schema of O associated to the
class C, E. The technique of attribute-oriented induc-
tion (Carter and Hamilton, 1998; Han et al., 1998)
was taken as inspiration for its simplicity and flexi-
bility. One remarkable common feature between such
technique and this one is that no restrictions are put
on the data. The first step of the algorithm is to de-
fine a mapping between each data of each dimension
and its generalized value, according to the conceptual
schema for instances of typeC. Then, the generalized
instances are formed, substituting each m-tuple with a
generalized m-tuple that constitutes the generalization
of the instances of the same type for each dimension.
5 INTERESTING CONCEPTUAL
SPACES
A conceptual space as previously defined allows users
to freely browse the conglomerate of objects and re-
view the aspects they consider more interesting. If the
Algorithm 1 Generation of multidimensional concep-
tual spaces.
Require: O , E, C, β
m
, β
M
{ O , instantiated ontology with Abox A ,
C, reference class to generate multidimensional spaces,
E, multidimensional schema,
β
m
, β
M
, minimum and maximum percentage of different
values in each dimension}
Ensure: E
′
{E
′
, multidimensional space associated to the schema E
and the ontology O }
First part: Eliminate the irrelevant dimensions and create
the generalization mappings between the data.
A
C
= {a|a ∈ C
I
}.
Iterate A
C
and group different data associated to each di-
mension of E.
if β
m
≥
|D
i
|
|A
C
|
≥ β
M
(D
i
must be removed) then
E = (D
1
,..., D
i−1
,D
i+1
,..., D
n
,c
φ
1
,..., c
φ
i−1
,c
φ
i+1
,..., c
φ
n
)
else
Generate mappings (d,d
′
) for each value d collected
in D
i
, d(d ↓
C
sup
i
d
′
) with C
sup
i
being one of the classes
direct ancestors of C
i
, d ∈ C
I
i
.
Second part: Creation of the multidimensional space
E
′
= {}
for all a ∈ A
C
do
Let t = (d
1
,...,d
n
) be the tuple of data associated to a,
according to E.
t
′
= (d
′
1
,...,d
′
n
), computed from the mapping gener-
ated in the previous step, being C
′
i
the type of data d
i
.
if ∃t
′′
= (d
′′
1
,...,d
′′
n
) ∈ E
′
, being C
′′
i
the type of data d
′′
i
such that ∀i ∈ {1,..,n} then
t
′′
= (d
′′
1
·
∪
t
d
′
1
,...,d
′′
n
·
∪
t
d
′
n
)
else
E
′
= E
′
∪ {t
′
}
data analyst were not informed on the features of the
object distribution in the domain, or if the number of
such features were too high, her analysis capabilities
would be strongly affected. Nevertheless, this prob-
lem can be overcome with an analysis tool able to
suggest to the user some interesting analysis dimen-
sions. This can be obtained with a customized feature
selection process. The concept of feature selection
was introduced for the task of dimensionality reduc-
tion originally defined in Statistics and widely studied
in Machine Learning.
Anyway, it is necessary to define a way of assess-
ing the importance of a given feature subset. The
measures more used in the literature are the informa-
tion gain , the Gini index , the uncertainty and the
correlation coefficients. Nevertheless, the large num-
ber of studies that argue in favor of decision trees and
information gain (like ID3 and C4.5), made us decide
to choose such a combination for our feature selec-
tion process. More exactly, in this work we propose
ICSOFT 2007 - International Conference on Software and Data Technologies
18

Let Cp be an ancestor concept in a dimension,
{C
1
,...C
n
} concepts directly specialized of Cp, and
objs a function which associates each concept with its
objects set. Let β be the percentage of maximum cor-
relation between the number of objects of descendant
and ancestor concepts.
If ∃C
i
such that |objs(C
i
)| ≥ β|objs(C
p
)|
Promote concepts C
1
,...,C
n
to level of concept C
p
Delete C
p
from the dimension.
Figure 3: Rules for filtering out uninteresting concepts.
to compute interesting conceptual multidimensional
schemata associated to a concept C by way of algo-
rithm 2, an adaptation of the one proposed by (Han
and Kamber, 2001). The purpose of such customized
algorithm is that of using the distributions of a set of
concepts in relation to a set of classes, in order to se-
lect the compositions of relations (paths) that assure
the highest information gain with respect to the distri-
bution. The main block of the algorithm is procedure
ComputePseudoSchemata which selects, as a first
step, the paths with highest information gain. Then,
for each path, the initial distribution is subdivided ac-
cording to the possible values of the data associated to
the objects through such path, and the process of sub-
division of the clusters is repeated while the informa-
tion gain is maintained in a desirable range. A parallel
task performed during this process is the computation
of the weights which indicate the interest estimation
for each conceptual schema that may be generated for
each path set.
A further filtering step can be done for each di-
mension taking into account the relation between the
quantity of objects associated to a concept and to its
ancestor concept. In this way, an uninteresting an-
cestor concept can be removed from the dimension,
following the rule described in Figure 3.
6 USING A MULTIDIMENSIONAL
CONCEPTUAL SPACE
As explained in the introduction, the major advantage
of a multidimensional space is that a user can see her
data from different points of view. Tabular models in
3D, function graphs, histograms and relational graphs
are the most natural tools to use for the analysis of
results. The possibility of realizing generalizations
and selections at each level also represents a powerful
analysis skill. In this way, it is possible to character-
ize object classes in relation to others, allowing for
the comparison and discovering of class features.
Although these are the analysis methods that have
traditionally been used, an analyst may be interested
Algorithm 2 Generation of interesting schemata of
multidimensional conceptual spaces.
Require: O , C, I, γ, α
{O , ontology with Abox A I
C, reference class for generating a schema of multidimen-
sional spaces,
γ, minimum allowed information gain
α, minimum number of objects in a description}
Ensure: SP
{SP, set of paths associated to C whose subsets can be
used to form interesting multidimensional schemata}
Let Paths
C
be the dictionary of paths starting fromC with
key in the destination concept.
S = {S
i
|S
i
= {a ∈ C
I
i
},∀C
i
,i ∈ {1,...,n},C ⊑ C
i
,
C
i
6= C
j
, j ∈ {1,..., n}, i 6= j}
SP = ComputePseudoSchemata(Paths
C
,S,γ)
function ComputePseudoSchemata(Paths
C
,S,γ) :
{Outputs a pair, in which the first element is a set of
paths and the second a real value indicating the impor-
tance of the set of paths for the generation of interesting
schemata}
First phase: Compute the importance of the current clus-
tering
ve =
∑
S
i
∈S
imp(S
i
), where
imp(S
i
) =
1, if |S
i
| > α
1− |S
i
|/α, otherwise
Second phase: Retrieve the subsets with highest informa-
tion gains
if |S| = 1 then
Output (
/
0,ve)
else
SP =
/
0
Compute information gain, G, for each destination
concept Paths
C
according to the classification in S
Let {path
1
,..., path
m
} be the set of paths which allow
a high discrimination between objects ordered accord-
ing to the gain value: G(path
1
) ≥ ... ≥ G(path
n
) >
γ and C
k
the destination concept associated to path
path
k
, k ∈ {1, ..., m}.
for all k ∈ {1,..., m} do
CD = {C
′
|C
′
⊑ C
k
}
for all C
′
∈ CD do
S = {S
Cl
C
′
= {a ∈ C
I
i
|C
i
∈ {1, ...,n},C ⊑ C
i
; a is
related to some data d according to path
i
∧ d ∈
C
′I
}}
SP = SP ∪
(sp,v)∈ComputePseudoSchemata(Paths
C
−{path
i
},S,γ)
{
h
C
i
∪ sp,v+ ve
i
}
Output SP
in other more complex insights about the behavior of
her data. Various pattern analysis tools have been de-
scribed in the literature, especially with the develop-
ment of data mining research. It is thus plausible to
create new algorithms for the extraction of interest-
ing patterns in the multidimensional conceptual envi-
ronment (Han and Kamber, 2001). Some of the most
ANALYSIS OF ONTOLOGICAL INSTANCES - A Data Warehouse for the Semantic Web
19

interesting patterns to extract are:
• of characterization: they represent rules for char-
acterizing a class of objects according to the val-
ues of a subset of its dimensions. They can be ex-
pressed by: class X ⇒ Condition[p
c
], where p
c
=
100×count(Condition)
n
, which means that, in class X,
Condition occurs in a p
c
percentage of the cases,
Count is a function that counts the number of
times in which a certain condition occurs, and n
is the total numbers of analyzed objects. p
c
is
known as characterization coefficient.
• of discrimination: they represent rules for char-
acterizing a class of objects for which a given
pattern is not observable with a certain fre-
quency in any other class. They can be ex-
pressed by: class X ⇐ Condition[p
d
], where p
d
=
100×count(Condition∧classX)
count(Condition)
. p
d
is known as discrim-
ination coefficient.
• association rules at different levels: they represent
rules for characterizing a class of objects in which
co-occurrence relations can be found in the at-
tributes of the multidimensional space. They can
be expressed by: Condition
1
⇒ Condition
2
[s,c],
where s =
100×count(Condition
1
∧Condition
2
)
n
,c =
100×count(Condition
1
)
count(Condition
1
∧Condition
2
)
, which means that in a
s% of the objects bothCondition
1
and Condition
2
are observed and that c% of objects satisfying
Condition
1
also satisfy Condition
2
. s is known as
the support of the rule and c as its confidence.
In order to customize these results to the model
we presented, the multidimensional conceptual model
must take into account how many objects in the con-
crete ontology are characterized by the description of
each cell.
7 CONCLUSION
The proposal of this paper is the formalization of a
data warehouse tool for the Semantic Web. The tool
is based on the theoretical foundations of Description
Logic and on the current developments of information
data generalization. Besides, an algorithm to gener-
ate interesting conceptual spaces according to the data
distribution is proposed. Ideas for adapting Data Min-
ing techniques in order to allow users a better knowl-
edge discovering from the Semantic Web have also
been exposed. Implementation of the proposal frame-
work, on which we are now working, consists of two
main components: 1) a reasoner (which works in an
off-line way) that retrieve instance models and ab-
straction functions from an ontology; and 2) a data
warehouse processor that use such models and func-
tions in order to perform all the necessary generaliza-
tions. This second module has been optimized con-
sidering some of the OLAP solutions.
ACKNOWLEDGEMENTS
This research has been partially supported by the
project TIN2005-09098-C05-04 (2006-2008).
REFERENCES
Abell
´
o, A. (2002). YAM
2
: A Multidimensional Concep-
tual Model. PhD thesis, Universitat Polit
´
ecnica de
Catalunya.
Baader, F. and Sattler, U. (2003). Description logics
with aggregates and concrete domains. Inf. Syst.,
28(8):979–1004.
Binh, N. T. and Tjoa, A. M. (2001). Conceptual mul-
tidimensional data model based on object-oriented
metacube. In SAC ’01: Proceedings of the 2001
ACM symposium on Applied computing, pages 295–
300. ACM Press.
Buzydlowski, J. W., Song, I.-Y., and Hassell, L. (1998).
A framework for object-oriented on-line analytic pro-
cessing. In DOLAP ’98: Proceedings of the 1st
ACM international workshop on Data warehousing
and OLAP, pages 10–15. ACM Press.
Carter, C. L. and Hamilton, H. J. (1998). Efficient attribute-
oriented generalization for knowledge discovery from
large databases. IEEE Transactions on Knowledge
and Data Engineering, 10(2):193–208.
Danger, R. (2007). Extracci
´
on y an
´
alisis de informaci
´
on
desde la perspectiva de la Web Sem
´
antica (Informa-
tion extraction and analysis from the viewpoint of
Semantic Web, in spanish). PhD thesis, Universitat
Jaime I.
Hacid, M.-S. and Sattler, U. (1998). Modeling multidimen-
sional databases: A formal object-centered approach.
In Proceedings of the Sixth European Conference on
Information Systems.
Han, J. and Kamber, M. (2001). Data Mining: Concepts
and Techniques. Morgan Kaufmann.
Han, J., Nishio, S., Kawano, H., and Wang, W. (1998).
Generalization-based data mining in object-oriented
databases using an object cube model. Data Knowl-
edge Engineering, 25(1-2):55–97.
Nguyen, T. B., Tjoa, A. M., and Wagner, R. (2000). An ob-
ject oriented multidimensional data model for OLAP.
In Web-Age Information Management, pages 69–82.
Trujillo, J., Palomar, M., G
´
omez, J., and Song, I.-Y. (2001).
Designing data warehouses with OO conceptual mod-
els. Computer, 34(12):66–75.
ICSOFT 2007 - International Conference on Software and Data Technologies
20
