A MULTI-OBJECTIVE GENETIC ALGORITHM FOR
CUTTING-STOCK IN PLASTIC ROLLS INDUSTRY
Ramiro Varela, César Muñoz, María Sierra
University of Oviedo. Department of Computing. Artificial Intelligence Centre. Campus of Viesques, 33271 Gijón, Spain
Inés González-Rodríguez
University of Cantabria. Department of Mathematics, Statistics and Computing. Los Castros s/n,39005, Santander, Spain
Keywords: Multi-objective optimization, Genetic Algorithms, Cutting Stock, Meta-heuristics.
Abstract: In this paper, we confront a variant of the cutting-stock probl
em with multiple objectives. It is an actual
problem of an industry that manufactures plastic rolls under customers’ demands. The starting point is a
solution calculated by a heuristic algorithm, termed SHRP that aims mainly at optimizing the two main
objectives, i.e. the number of cuts and the number of different patterns; then the proposed multi-objective
genetic algorithm tries to optimize other secondary objectives such as changeovers, completion times of
orders weighted by priorities and open stacks. We report experimental results showing that the multi-
objective genetic algorithm is able to improve the solutions obtained by SHRP on the secondary objectives
and also that it offers a number of non dominated solutions, so that the expert can chose one of them
according to his preferences at the time of cutting the orders of a set of customers.
1 INTRODUCTION
This paper deals with a real Cutting-Stock Problem
(CSP) in manufacturing plastic rolls. The problem is
a variant of the classic CSP, as it is usually
considered in the literature, with additional
constraints and objective functions We have solved
this problem in (Puente et al. 2005, Varela et al.
2006 ) by means of a GRASP algorithm (Resende
and Ribeiro, 2002) termed Sequential Heuristic
Randomized Procedure (SHRP), which is similar to
other approaches such as the SVC algorithm
proposed in (Belov and Scheithauer, 2006). Even
though SHRP tries to optimize all objective
functions, in practice it is mainly effective in
optimizing the main two ones: the number of cuts
and the number of patterns. It is due to SHRP
considering all objective functions in a hierarchical
way that it pays much more attention to the first two
ones than to the remaining. In this work we propose
a Multi-Objective Genetic Algorithm (MOGA) that
starts from a solution computed by SHRP algorithm
and tries to improve it regarding three secondary
objectives: the cost due to changeovers or setups, the
orders’ completion time weighted by priorities and
the maximum number of open stacks.
Generated
rolls
Cutting
knives
Maximum width
Trim loss
Film
movement
Bi
g
roll
Pressure rollers
Trim loss
Generated
rolls
Minimum width
Figure 1: Working schema of the cutting-machine.
The paper is organized as follows. Next section
is devoted to briefly describe the production process
of plastic rolls. In section 3, the problem formulation
is given. As this formulation is rather complex, in
186
Varela R., Mu
˜
noz C., Sierra M. and Gonz
´
alez-Rodr
´
ıguez I. (2007).
A MULTI-OBJECTIVE GENETIC ALGORITHM FOR CUTTING-STOCK IN PLASTIC ROLLS INDUSTRY.
In Proceedings of the Second International Conference on Software and Data Technologies - PL/DPS/KE/WsMUSE, pages 186-193
Copyright
c
SciTePress

section 4 we have introduced an example to clarify
both the formulation and the whole process of
obtaining a solution. In section 3, the main
characteristics of the proposed MOGA are
described. In section 4, we report results from a
experimental study. Finally, in section 5, we
summarize the main conclusions and some ideas for
future work.
2 PRODUCTION PROCESS
Figure 1 shows the schema of the cutting machine.
A number of rolls are cut at the same time from a
big roll according to a cutting pattern. Each roll is
supported by a set of cutting knives and a pressure
roller of the appropriate size. At each of the borders,
a small amount of product should be discarded,
therefore there is a maximum width that can be used
from the big roll. There is also a minimum width,
due to the capability of the machine to manage trim
loss. Moreover, a maximum number of rolls can be
cut at the same time. When the next cut requires a
different cutting pattern, the process incurs in a setup
cost due to changing cutting knives and pressure
rollers.
The problem has also a number of constraints
and optimization objectives that make it different
from conventional formulations. For example
underproduction is not allowed and the only
possibility for overproduction is a stock declared by
the expert. Once a cut is completed, the rolls are
packed into stacks. The stack size is fixed for each
roll width, so a given order is composed by a
number of stacks, maybe the last one being
uncompleted. Naturally, only when a stack is
completed it is taken away from the proximity of the
cutting machine. So, minimizing the number of open
stacks is also convenient in order to facilitate the
production process. Moreover, some orders have
more priority than others. Consequently the delivery
time of orders pondered by the client priority is an
important criterion as well.
3 PROBLEM FORMULATION
The problem is a variant of the One Dimensional
Cutting-Stock Problem, also denoted 1D-CSP. In
(Gilmore and Gomory, 1961) the first model is
proposed for this problem. It is defined by the
following data: (m, L, l=(l
1
,...,l
m
), b = (b
1
,...,b
m
)),
where L denotes the length of each stock piece (here
the width of the big roll), m denotes the number of
piece types (orders) and for each type i=1,…,m, l
i
is
the piece length (roll width), and b
i
is the order
demand. A cutting pattern describes how many
items of each type are cut from a stock length. Let
column vectors A
j
=(a
1j
,…,a
mj
) ∈ Ζ
+
m
, j=1,…,n,
represent all possible valid cutting patterns, i.e. those
satisfying
∑
=
≤
mi
iij
Lla
,...,1
where a
ij
is the number of pieces of order i that are
generated by one application of the cutting pattern
A
j
. Let x
j
, j=1,…,n, be the frequencies, i.e. the
number of times each pattern is applied in the
solution. The model of Gilmore and Gomory aims at
minimizing the number of stock pieces, or
equivalently minimizing the trim-loss, and is stated
as following
∑
=
−
=
nj
j
CSPD
xz
,...,1
1
min
mibxats
i
nj
jij
,...,1,..
,...,1
=≥
∑
=
njx
j
,...,1,Ζ =
∈
+
From this formulation, the problem is usually
solved by Linear Programming based methods
(Umentani et al. 2003). However, this model is not
directly applicable to our case mainly due to the
non-overproduction constraint, but it can be easily
adapted as we will see in the sequel. We start by
giving a detailed formulation of the main problem;
that considering all characteristics and optimization
criteria relevant from the point of view of the
experts. As the number of optimization criteria is too
large to deal with all of them at the same time and
the search space could be very large, we have opted
by introducing a simplified problem; i.e. a problem
with a lower number of objective functions and also
with a smaller search space in general. Once the
simplified problem is solved, the solution will be
adapted to the original problem; in this process all
the objectives will be considered.
3.1 The Main Problem
In order to clarify the problem definition, we present
the data of the machine environment and the clients’
orders, the form and semantics of a problem
solution, the problem constraints and the
optimization criteria in the hierarchical order in
which they are usually considered by the expert.
Given
• The set of parameters of the cutting machine:
the maximum width of a cut L
max
, the minimum
A MULTI-OBJECTIVE GENETIC ALGORITHM FOR CUTTING-STOCK IN PLASTIC ROLLS INDUSTRY
187

width of a cut L
min
, the maximum number of
rolls that can be generated in a cut C
max
, the
minimum and the maximum width of a single
roll, W
min
and W
max
respectively, and the
increment of width
Δ
W between two
consecutive permitted roll widths.
• The setup costs. There is an elementary setup
cost SC and some rules given by the expert that
allows calculating the total setup cost from a
configuration of the cutting machine to the next
one. The setup cost is due to roller and cutter
changes as follows. The cost of putting in or
taking off a pressure-roller is SC; the cost of
putting in an additional knife is 3SC, and the
cost of dismounting a knife is 2SC.
• The types of pressure-rollers PR =
{PR
1
,…,PR
p
} and the mapping F
PR
from roll
widths to pressure-rollers.
• The mapping F
ST
from roll widths to stack sizes
or number of rolls in each stack unit.
• The orders description given by (M={1,...,m},
b = (b
1
,...,b
m
) , l=(l
1
,...,l
m
), p=(p
1
,...,p
m
)) where
for each order i = 1,…,m, b
i
denotes the
number of rolls, l
i
denotes the width of the rolls
and p
i
the order priority.
• The stock allowed for overproduction (S
={m+1,...,m+s}, bs = (b
m+1
,...,b
m+s
), ls =
(l
m+1
,...,l
m+s
)) where for each i=1,…,s, b
m+i
denotes the number of rolls of type m+i allowed
for overproduction and l
m+i
denotes the width of
these rolls.
• The set of feasible cutting patterns, for the
orders and stock given, A where each A
j
∈A is,
A
j
=(a
1j
,…,a
mj
,a
(m+1)j
,…,a
(m+s)j
) ∈ Ζ
+
m+s
and
denotes that, for each i=1,…,m+s, a
ij
rolls of
order i are cut each time the cutting pattern A
j
is
applied. A cutting pattern A
j
is feasible if and
only if both of the following conditions hold
∑
∪∈
≤=≤
SMi
iijj
LlaLL
maxmin
,
∑
∪∈
≤=
SMi
ijj
CaC
max
being L
j
and C
j
the total width and the number
of rolls of pattern A
j
respectively. D
j
= L
max
– L
j
denotes the trim-loss of the cutting pattern.
The objective is to obtain a cutting plan (Π, x),
where Π=(A
1
,…,A
|Π|
)∈A
|Π|
and x = (x
1
,...,x
|Π|
) ∈Ζ
+
|Π|
denotes the pattern frequencies. The cutting patterns
of Π are applied sequentially, each one the number
of times indicated by its frequency. A
j
l
, 0≤j≤|Π|,
0≤l≤x
j
, denotes the lth cut corresponding to pattern
A
j
and CI(A
j
l
) is the cut index defined as
(
)
∑
−=
+=
1,...,1 jk
k
l
j
lxACI
Given an order i∈M its first roll is generated in cut
A
j
1
such that A
j
is the first pattern of Π with a
ij
≠ 0,
this cut is denoted CU
start
(i). Analogously, the last
roll of order i is generated in cut A
k
xk
so that A
k
is the
last pattern of Π with a
ik
≠ 0, this cut is denoted
CU
end
(i).
As we have considered feasible cutting patterns,
the only constraint that should be required to a
solution is the following
• The set of rolls generated by the application of
the cutting plan (Π, x) should be composed by
all rolls from the orders and, eventually, by a
number of rolls from the stock. That is, let s
i
is
the number of rolls of stock i
∈
S in the solution
∑
=∈∀
∈
jiji
xasSi ,
ΠA
j
Then, the constraint can be expressed as
follows:
∑
∈
=∈∀
ΠA
ijij
j
bxaMi
,
ii
bsSi ≤≤∈∀ 0,
Regarding objective functions, as we have remarked,
we consider two main functions
1. Minimize the number of cuts, given by
∑
j=1,…,|Π|
x
j
. The optimum value is denoted
z
1D-CSP
.
2. Minimize the setup cost, given by ∑
j=1,…,|Π|
SU(A
j-1
, A
j
), where SU(A
j-1
, A
j
) denotes the
setup cost from pattern A
j-1
to pattern A
j
calculated as it is indicated above.
Configuration A
0
refers to the situation of the
cutting machine previous to the first cut.
And two secondary functions
3. Minimize the completion times of orders
weighted by their priorities given by
()()
∑
∈Mi
endi
iCUCIp
4. Minimize the maximum number of open stacks
along the cut sequence. Let R(i,A
j
l
) denote the
number of rolls of order i generated from the
beginning up to completion of cut A
j
l
(
)
laxaAiR
ij
jk
kik
l
j
+=
∑
−= 1,..,1
,
and let OS(i,A
j
l
) be 1 if after cut A
j
l
there is an
open stack of order i and 0 otherwise. Then, the
ICSOFT 2007 - International Conference on Software and Data Technologies
188

maximum number of open stacks along the cut
sequence is given by
(
)
∑
∈
=Π=
Mi
l
j
xlj
AiOS
j
,max
,...,0|,|,...,1
3.2 The Simplified Problem
In the main problem, as formulated in the previous
section, it is often the case that two or more orders
have the same width or a stock has the same width
as one of the orders. So, from the point of view of
the cutting process, two cutting patterns A
i
and A
j
are
equivalent if both patterns define the cutting of the
same number of rolls of the same sizes, i.e. given the
set of widths L = {l
e
, e∈M∪S}, with cardinal |L|=
ms, ms≤m+s we have
LlaaAA
llsmk
kj
llsmk
ki
ji
kk
∈∀=⇔≡
∑∑
=+==+=
,
,...,0,,...,0
Now the simplified problem can be stated as
follows. Given
• The set of parameters of the cutting machine,
the setup costs, the types of pressure-rollers and
mapping F
PR
: as they are in the main problem
and the mapping function F
ST
as they are in the
main problem.
• The simplified orders description given by
(M’={1,...,m’}, b’ = (b’
1
,...,b’
m’
) ,
l’=(l’
1
,...,l’
m’
)), where for each order i = 1,…,m’,
b’
i
denotes the number of rolls and l’
i
∈L
denotes the width of the rolls. The simplified
orders list b’ are obtained from the original
order list b so as
∑
==
=
ik
llmk
ki
bb
',...,1
'
• The stock allowed for overproduction (S’
={m’+1,...,m’+s}, bs’ = (b’
m’+1
,...,b’
m’+s
), ls’ =
(l’
m’+1
,...,l’
m’+s
)) where for each i=1,…,s, b’
m’+i
=
b
m+i
denotes the number of rolls of type m’+i
allowed for overproduction and l’
m’+i
= l
m+i
∈L
denotes the width of these rolls (notice that two
different stock orders cannot have the same
width). Here both l’ and ls’ are lists with no
repeated elements, so they can be seen as sets
such that l’∪ls’=L, although, it is possible that
l’∩ls’≠∅. In what follows, we assume L to be
ordered, beginning with l’
1
,...,l’
m’
followed by
the elements from ls’ that do not belong to l’.
L=(l’
1
,….., l’
ms
), ms≤m’+s.
• The set of simplified feasible cutting patterns
for the simplified orders and stock given, E,
obtained from the set of feasible cutting patterns
for the original problem A, |E|≤|A|, where
every E
j
∈ E is E
j
=(e
1j
,…,e
msj
) ∈ Ζ
+
ms
meaning
that, for each i=1,…,ms, e
ij
rolls of width l’
i
are
cut each time the cutting pattern E
j
is applied. In
other words, each element of E is an
equivalence class of the quotient set of A with
the above relation, so it is a simplified
representation of a number of cutting patterns of
A.
The objective is to obtain a simplified cutting plan
(Π’,x’), where Π’=(E
1
,…,E
|Π’|
)∈ E
|Π’|
and
x’=(x’
1
,...,x’
|Π’|
)∈Ζ
+
|Π’|
denotes the pattern
frequencies.
As all the simplified cutting patterns are feasible,
the only constraint that should be requited to a
solution is the following
• The set of rolls generated by the application of
the simplified cutting plan (Π’, x’) should be
composed by all rolls from the orders and,
eventually, by a number of rolls from the stock.
That is, let s’
i
the number of rolls of stock of
width l’
i
in the solution, being 0 if there is no
m’+k ∈S’ such that l’
i
=l’
m’+k
,
∑
∈
=+∈∀
'
''},,..,1'{
ΠE
jiji
j
xesmsmi
Then, the constraint can be expressed as
follows:
∑
∈
+=∈∀
'
''','
ΠE
iijij
j
sbxeMi
,
0≤ s’
i
≤b’
m’+k
The objective functions are
1. Minimize the number of cuts calculated by
∑
j=1,…,|Π’|
x’
j
.
2. Minimize the number of simplified cutting
patterns |Π’|.
3. Maximize the amount of stock generated, that is
∑
i=1,..,ms
l’
i
s’
i
, so the trim-loss is minimized for a
given number of cuts.
Now let us to clarify how a solution of the simplified
problem can be transformed in a solution to the main
problem. To do so, we have to map each simple cut
from a simplified pattern E
j
to any of the cuts of
pattern A
k
of the equivalence class defined by E
j
. In
doing so, we can consider different orderings in the
simplified cutting plan, and also different orderings
between the single cuts derived from a simplified
cutting pattern, in order to satisfy all the
optimization criteria of the main problem. As we can
A MULTI-OBJECTIVE GENETIC ALGORITHM FOR CUTTING-STOCK IN PLASTIC ROLLS INDUSTRY
189

observe, objectives 1 and 3 are the same in both
problems, but objective 2 is different. The reason to
consider objective 2 in the simplified problem is that
minimizing the number of patterns |Π’| it is expected
that the setup cost of the main problem is to be
minimized as well. This is because the setup cost
between two consecutive cuts A
k
and A
l
of the main
problem is null if both A
k
and A
l
belongs to the same
equivalence class E
j
.
To solve this simplified problem, in (Puente et al.
2005 and Varela et al. 2007) we have proposed a
GRASP algorithm. Then, the solution given by this
algorithm is transformed into a solution to the main
problem by a greedy algorithm that assigns items to
actual orders so as to optimize objectives 2, 3, and 4
in hierarchical order, while keeping the values of the
first two objectives. To be more precise, we clarify,
in the next section, how a simplified solution is
transformed into an actual solution by means of an
example.
4 AN EXAMPLE
In this section we show an example to clarify the
whole process of obtaining a cutting plan for the
main problem and, in particular, how a simplified
solution is transformed in a solution to the main
problem by MOGA. The problem data and final
results are displayed as they are by the application
program. Figure 2 shows an instance and the
corresponding simplified problem. A real instance is
given by a set of orders, each one defined by a client
name, a client identification number, the number of
rolls, the width of the rolls and the order priorities.
Additionally, the maximum and minimum allowed
width of a cut should be given, in this case 5500 and
5700 respectively and also a stock description to
choose a number of rolls from if it is necessary to
obtain valid cutting patterns. In this example up to
10 rolls of each width 1100, 450 and 1150 could be
included in the cutting plan. Furthermore, some
other parameters (not shown in Figures) are
necessary, for instance, two additional data should
be given to evaluate the number of open stacks and
setup cost: the number of rolls that fit in a stack
(mapping F
ST
) and the correspondence between the
size of pressure rollers and the width of the
supported rolls (mapping F
PR
). Here we have
supposed that every stack contains 4 rolls and that
the correspondence between pressure roller types
and width rolls is the following: type 1 (0-645), type
2 (650-1045), type 3 (1050-1345), type 4 (1350-
1695). All the allowed widths are multiples of 5 and
the minimum width of a roll is 250 while the
maximum is 1500. Finally, the maximum number of
rolls in a pattern is 10.
a)
b)
Figure 2: An example of problem data (main and
simplified instance).
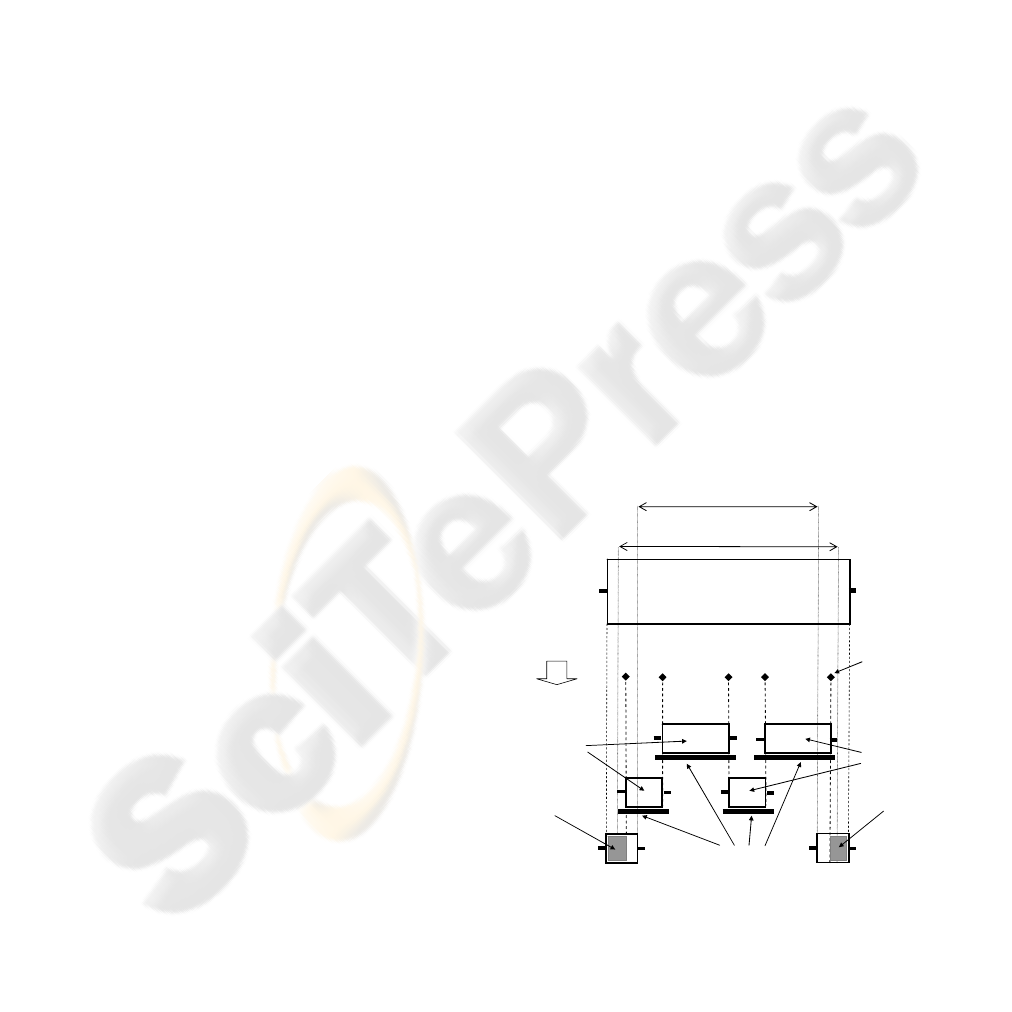
As we can observe in Figure 1, the main instance
with 10 orders is reduced to a simplified instance
with only 6 orders. This is a conventional 1D-CSP
instance with two additional constraints: the
maximum number of rolls in a pattern and the
minimum width of a pattern. Figure 2 shows a
solution to the simplified problem with 21 cuts and 4
different patterns, where 3 stock rolls have been
included in order that the last pattern to be valid.
Figure 3 shows the final solution to the main
problem. The figure shows the order identifiers,
where 0 represents to the stock. A solution is a
sequence of cutting patterns, where each pattern
represents not only a set of roll widths, but also the
particular order the roll belongs to. The actual
solution is obtained from a simplified solution by
means of a greedy algorithm that firstly considers
the whole set of individual cuts as they are expressed
in the simplified solution. Then it assigns a customer
order to each one of the roll widths in the simplified
cuts, and finally considers all different actual
patterns maintaining the order derived from the
simplified solution. The MOGA proposed in this
paper starts from this solution and tries to improve it
by considering different ordering of the cutting
patterns.
ICSOFT 2007 - International Conference on Software and Data Technologies
190

Figure 3: A cutting plan for the problem of Figure 2.
The changeover of each pattern refers to the cost
of putting in and out cutting knives and pressure
rollers from the previous pattern to the current one.
As we can observe, the first pattern has a
changeover cost of 28 because it is assumed that it is
necessary to put in all the 7 cutting knives and 7
pressure rollers before this pattern. In practice, this
is not often the case as a number of cutting knives
and pressure rollers remain in the machine from
previous cuts. Regarding open stacks, each column
shows the number of them that remain incomplete in
the proximity of the machine from a cut to the next
one, i.e. when a stack gets full after a cut, or it is the
last stack of an order, it is not considered.
5 MULTIOBJECTIVE GENETIC
ALGORITHM
According to the previous section, the encoding
schema is a permutation of the set of patterns
comprising a solution. So, each chromosome is a
direct representation of a solution, which is an
alternative to the initial solution produced by the
greedy algorithm. The initial solution is the one of
Figure 3 which is codified by chromosome (1 2 3 4 5
6 7 8 . . . 21), i.e. each gene represents a single cut.
As objectives 2, 3 and 4 depend on the relative
ordering of patterns and also on their absolute
position in the chromosome sequence, we have used
simple genetic order based operators (Goldberg,
1989, chap. 5) that maintain these characteristics
from parents to offsprings.
The algorithm structure is quite similar to a
conventional single GA: it uses generational
replacement and roulette wheel selection. The main
differences are due to its multi-objective nature. The
MOGA maintains, apart from the current population,
a set of non dominated chromosomes. This set is
updated after each generation, so that it finally
contains an approximation of the pareto frontier for
the problem instance.
In order to assign a single fitness to each
chromosome, the whole population is organized into
dominant groups as it follows. The first group is
comprised by the non dominated chromosomes. The
second group is comprised by the non dominated
chromosomes from the remaining population and so
on. The individual fitness is assigned so that a
chromosome in a group has a larger value than any
chromosome in the subsequent groups. Moreover,
inside each group, the fitness of a chromosome is
adjusted by taking into account the number of
chromosomes in its neighbourhood in the space
defined by the three objective functions. The
chromosomes’ neighbors are those that are in the
chromosome’s niche count. The evaluation
algorithm is as it follows.
Step 0. Set F to a value sufficiently large
Step 1. Determine all non-dominated chromosomes
Pc from the current population and assign F to
their fitness.
Step 2. Calculate each individual’s niche count m
j
:
(
)
∑
∈
=
c
Pk
jkj
dshm
where
()
(
)
⎩
⎨
⎧
<−
=
otherwise0
if1
2
sharejksharejk
jk
dd
dsh
σσ
and d
jk
is the phenotypic distance between two
individuals j and k in Pc and
σ
share
is the
maximum phenotypic distance allowed between
any two chromosomes of Pc to become
members of a niche.
Step 3. Calculate the shared fitness value of each
chromosome by dividing it fitness value by its
niche count.
Step 4. Create the next non dominated group with
the chromosomes of Pc, remove these
chromosomes from the current population, set F
to a value lower than the lowest fitness in Pc, go
to step 1 and continue the process until the
entire population is all sorted.
This evaluation algorithm is adapted from (Zhou and
Gen, 1999). In their paper, G. Zhou and M. Gen
A MULTI-OBJECTIVE GENETIC ALGORITHM FOR CUTTING-STOCK IN PLASTIC ROLLS INDUSTRY
191

propose a MOGA for the Multi-Criteria Minimum
Spanning Tree (MCMSP). In the experimental study
they consider only two objective functions.
In order to compute d
jk
and
σ
share
values we
normalize distances in each one of the three
dimensions to take values in [0,1]; this requires
calculating lower and upper bounds for each
objective. The details of these calculations are given
in (Muñoz, 2006). Also, we have determined
empirically that
σ
share
= 0,5 is a reasonable choice.
6 EXPERIMENTAL STUDY
In this section we present results from some runs of
a prototype implemented in (Muñoz, 2006) for the
problem instance of Figure 2. The program is coded
in Builder C++ for Windows and the target machine
was Pentium 4 at 3,2 Ghz. with HT and 1Gb of
RAM.
Table 1: Summary of results from three runs of MOGA
starting from the solution of Figure 3 for the problem of
Figure 1. Parameters of MOGA refer to /Population
size/Number of generation/, the remaining Crossover
probability/Mutation probability/
σ
share
are 0,9/0,1/0,5.
Each cell shows the cost of /changeovers/weighed
times/maximum open stacks.
Run 1 2 3
Pars. /200/200/ /500/500/ /700/700/
Time(s.) 37 649 1930
49/188/6 47/176/6 39/172/6 (*)
49/186/7 47/184/5 (*) 47/184/5 (*)
44/196/5 (*) 39/179/7
Pareto
frontier
reached
45/184/6
(*) These values represent solutions non-dominated by
any other reached in all three runs
In the first set of experiments, the MOGA starts
from the solution of Figure 2. Table 1 summarizes
the values of the three objective functions
(changeovers, weighed time and maximum open
stacks) for each of the solutions in the approximate
pareto frontier obtained in three runs with different
parameters. As we can observe, the quality of the
solutions are in direct ratio with the processing time
given to the MOGA. The values of objective
functions for the initial solution of Figure 3 are
47/188/5, which is dominated by some of the
solutions of Table 1. So, it is clear that it is possible
to improve on secondary objectives in solutions
obtained by procedure SHRP.
Table 2: Summary of results of MOGA starting from 9
different simplified solutions to the instance of Figure 2a
with the same values of number of cuts (21) and patterns
(4), except solution 6 which has 3 patterns, with different
amount of stock generated. For each instance, two runs
have been done with parameters /500/500/0,9/0,1/0,5, the
first (Normal) in the same conditions as before; while in
the second, the niche count is not computed but it is taken
as 1 in all cases.
Inst. Initial Normal Niche c. = 1
1 39/184/5 38/174/5 (*) 55/188/6
38/197/4 (*) 42/212/8
48/199/6
50/197/5
49/190/6
52/190/5
48/201/5
2 39/187/5 38/174/5 (*) 38/174/5 (*)
38/197/4 (*)
3 43/187/5 42/174/5 (*) 42/174/5 (*)
42/197/4 (*)
4 46/185/5 43/185/5 (*) 55/177/5 (*)
5 56/185/5 55/177/5 (*) 54/194/7 (*)
63/182/6
6 36/186/5 38/177/5 (*) 38/177/5 (*)
7 56/192/5 50/188/5 (*) 50/203/5
50/197/6
50/195/7
8 55/213/5 61/193/5 56/181/5 (*)
63/179/6 (*) 52/182/5 (*)
70/188/5 67/173/5 (*)
71/179/5 63/179/6 (*)
60/180/6 (*) 62/180/6
71/178/6
61/193/5
9 42/201/6 (*) 54/180/6 51/177/7 (*)
46/181/5 (*) 52/176/7 (*)
55/180/5 44/181/6 (*)
44/182/5 (*) 53/172/7 (*)
60/179/6 54/169/7 (*)
59/183/4 (*) 54/173/5 (*)
(*) These values represent solutions non-dominated by
any other reached from the same simplified solution
In the second set of experiments, we have taken
9 more simplified solutions, different from that of
Figure 2b, and have applied MOGA to each of them
with the same parameters as in the second run of
Table 1. In these experiments, we have considered
also the MOGA without fitness adjustment, i.e. by
considering a niche count equal to 1 in all cases. The
results are summarized in Table 2. As we can
observe, in general, MOGA reaches better solutions
with fitness adjustment, even though it takes a larger
time (about 640 s. versus 600 s.). Only for instances
ICSOFT 2007 - International Conference on Software and Data Technologies
192

8 and 9 is the version without fitness adjustment
equal or better. On the contrary, for instance 1 the
results without fitness adjustment are clearly much
worse. These results show that MOGA is able to
reach solutions better than the initial one. Here it is
important to remark that the initial solution is not
included into the initial population of MOGA and
that this population is completely random; i.e. all
cuts are randomly distributed, what usually
translates into a very high changeover cost. In
practice, good solutions tend to aggregate equal cuts
consecutively in order to minimize changeovers.
This fact could be exploited when generating the
initial population in order to reduce the computation
time required by MOGA.
Also, these results suggest that the neighborhood
strategy should be reconsidered, in particular that a
static value for parameter
σ
share
is not probably the
best choice.
7 CONCLUSIONS
In this paper we have proposed a multi-objective
genetic algorithm (MOGA) which aims to improve
solutions to a real cutting stock problem obtained
previously by another heuristic algorithm. This
heuristic algorithm, termed SHRP, focuses mainly
on the two main objectives and considers them
hierarchically. Then, the MOGA tries to improve
other three secondary objectives at the same time,
while keeping the values of the main objectives. We
have presented some results over a real problem
instance showing that the proposed MOGA is able to
improve the secondary objective functions with
respect to the initial solution, and that it offers the
expert a variety of non-dominated solutions.
As future work, we plan reconsidering the
MOGA strategy in order to make it more efficient
and more flexible so that it can take into account the
preferences of the experts with respect to each one
of the objectives. In order to improve efficiency we
will try to devise local search techniques and
initialization strategies based on heuristic
dispatching rules. Also, we will consider alterative
evolution strategies for multi-objective optimization
(Goldberg, 1985, Chapter 5) and other multi-
objective search paradigms such as exact methods
based on best first search (Mandow and Pérez-de-la-
Cruz, 2005). In this way we could compare different
strategies for this particular problem.
ACKNOWLEDGEMENTS
This research has been partially supported by
contract CN-05-127 of the University of Oviedo and
the company ERVISA, and by FICYT under
research contract FC-06-BP04-021.
REFERENCES
Belov, G., Scheithauer, G. 2006b. Setup and Open Stacks
Minimization in One-Dimensional Stock Cutting.
(submited to INFORMS Journal of Computing).
Gilmore, P. C., Gomory, R. E., 1961. A linear
programming approach to the cutting stock problem.
Operations Research 9, 849-859.
Goldberg, D. E. 1989. Genetic Algorithms in Search,
Optimization and Machine Learning. Addison-Wesley.
Mandow, L., Pérez-de-la-Cruz, J.L. 2005. A new approach
to multiobjective A* search. IJCAI-05 19th Int. Joint
Conf. on Artificial Intelligence, 218-223.
Muñoz, C., 2006. A Multiobjective Evolutionary
Algorithm to Compute Cutting Plans for Plastic Rolls.
Degree project, University of Oviedo, School of
Computing, Gijón (In Spanish).
Puente, J., Sierra, M., González-Rodríguez, I., Vela, C. R.,
Alonso, C., Varela, R., 2005.
An actual problem in
optimizing plastic rolls cutting.
Workshop on
Planning, Scheuling and Temporal Reasoning, in
CAEPIA 2005. Santiago de Compostela.
Resende, M. G. C., Ribeiro, G. C., 2002. Greedy
randomized adaptive search procedures. In F. Glover
and G. Kochenberg eds. Handbook of Metaheuristics,
p. 219-249. Kluwer Academic Publishers.
Varela, R. Vela, C. R., Puente, J. Sierra, M. R. González-
Rodríguez, I., 2007.
An effective solution for an actual
cutting stock problem in manufacturing plastic rolls.
(submitted to Annals of Operations Research).
Umetani, S. Yagiura, M., Ibaraki, T., 2003. One-
dimensional cutting stock problem to minimize the
number of different patterns. European Journal of
Operational Research 146, 388-402.
Zhou, G., Gen, M., 1999. Genetic algorithm approach on
multi-criteria minimum spanning tree problem.
European Journal of Operational Research 114, 141-
152.
A MULTI-OBJECTIVE GENETIC ALGORITHM FOR CUTTING-STOCK IN PLASTIC ROLLS INDUSTRY
193
