SOFTWARE DEFECT PREDICTION: HEURISTICS FOR

WEIGHTED NAÏVE BAYES

Burak Turhan and Ayşe Bener

Department of Computer Engineering, Bogazici University, 34342 Bebek, Istanbul, Turkey

Keywords: Empirical software engineering, Software quality, Defect prediction, Software metrics, Naïve Bayes,

Feature weighting.

Abstract: Defect prediction is an important topic in software quality research. Statistical models for defect prediction

can be built on project repositories. Project repositories store software metrics and defect information. This

information is then matched with software modules. Naïve Bayes is a well known, simple statistical

technique that assumes the ‘independence’ and ‘equal importance’ of features, which are not true in many

problems. However, Naïve Bayes achieves high performances on a wide spectrum of prediction problems.

This paper addresses the ‘equal importance’ of features assumption of Naïve Bayes. We propose that by

means of heuristics we can assign weights to features according to their importance and improve defect

prediction performance. We compare the weighted Naïve Bayes and the standard Naïve Bayes predictors’

performances on publicly available datasets. Our experimental results indicate that assigning weights to

software metrics increases the prediction performance significantly.

1 INTRODUCTION

Quality of software is often measured by the number

of defects in the final product. Minimizing the

number of defects—maximizing software quality—

requires a thorough testing of the software in

question. On the other hand, testing phase requires

approximately 50% of the whole project schedule

(Harold, 2000; Tahat et.al., 2001). This means

testing is the most expensive, time and resource

consuming phase of the software development

lifecycle. An effective test strategy should therefore

consider minimizing the number of defects while

using resources efficiently.

Defect prediction models are helpful tools for

software testing. Accurate estimates of defective

modules may yield decreases in testing times and

project managers may benefit from defect predictors

in terms of allocating the limited resources

effectively (Song et.al., 2006).

Defect predictors based on linear regression

(Munson and Khoshgoftaar, 1990), discriminant

analysis (Munson and Khoshgoftaar, 1992), decision

trees, neural networks (Padberg et.al., 1998;

Khoshgoftaar and Seliya, 2004) and Naïve Bayes

classification (Menzies et.al., 2007) have been

analysed in previous research. Among these, Naïve

Bayes is reported to achieve significantly better

performances than the other methods (Menzies et.al.,

2007). Naïve Bayes assumes the independence and

equal importance of provided features despite the

fact that these do not hold in many cases.

Nevertheless, Naïve Bayes has a good reputation for

its prediction accuracy (Domingos and Pazzani,

1997).

This paper attempts to tackle the equal

importance of features assumption of Naïve Bayes.

As shown in previous research, all software metrics

may not be good indicators of software defects

(Basili et.al., 1996). We extend this and assume that

all software metrics may not have equal effect on

defect prediction and they should be treated

accordingly. Our research goal is to develop a

methodology that permits the use of software

metrics in terms of their relevance to defect

prediction. For this purpose we present one existing

and two new heuristics for determining the degree of

importance of software metrics and we evaluate

these in Weighted Naïve Bayes classifier on

datasets, which are chosen among real software

applications and publicly provided by NASA MDP

(Nasa, 2007).

244

Turhan B. and Bener A. (2007).

SOFTWARE DEFECT PREDICTION: HEURISTICS FOR WEIGHTED NAÏVE BAYES.

In Proceedings of the Second International Conference on Software and Data Technologies - SE, pages 244-249

DOI: 10.5220/0001339402440249

 SciTePress

2 RELATED WORK

Linear regression analysis for defect prediction

treats software metrics as the independent variables

in order to estimate the dependent variable i.e. defect

density. Munson and Khoshgoftaar (1992)

investigate linear regression models and

discriminant analysis to conclude the performance of

the latter is better. They use Principal Component

Analysis (PCA) as a pre-processing step in order to

eliminate the co-linearity in software metrics.

Nagappan et.al. (2005) also uses linear regression

analysis with PCA for the STREW metric suite.

Decision tree learning is another common method

that is preferred for its rule generation capabilities

(Menzies et.al., 2003; Menzies et.al., 2004). Such

rules are easier to explain to non-technical people

(Fenton and Neil, 1999).

Though some research stated against using static

code measures (Fenton and Ohsson, 2000; Shepperd

and Ince, 1994), a recent research showed that using

a Naïve Bayes classifier with log-filtered static code

measures yields significantly better results than rule

based methods like decision trees (Menzies et.al.,

2007).

The number of researches for relaxing the

assumptions of Naive Bayes have significantly

increased in recent years. These researches focused

on modifications to break the conditional

independence assumption and weighting attributes

(Lewis, 1998; Zhang and Webb, 2000; Frank et.al,

2003; Zhang and Sheng, 2004; Hall, 2007). All

studies reported results that are generally ‘not worse’

than the standard Naïve Bayes, while preserving the

simplicity of the model.

As for the attributes that are used for

constructing predictors, some researches prefer

ranking the features for feature subset selection

(Mladenic and Grobelnik, 1999; Menzies et.al.,

2007), and there are also researches on using the

ranking criteria for feature weight assignment

(Zhang and Sheng, 2004; Auer et.al., 2006). In fact,

feature subset selection corresponds to ‘hard’

weighting of features, i.e. assigning 0 or 1 for

feature weights.

In this paper, we aim at combining the best

practices of the above mentioned studies for

constructing robust and accurate defect predictors,

by means of using a weighted Naïve Bayes classifier

and constructing heuristics for accurate feature

weight assignment. While above mentioned

researches employ feature subset selection based on

the estimated importance of features, they treat the

selected subset of features equally. On the other

hand, we propose to treat each feature based on their

estimated importance and we search for empirical

evidence for the validity of our approach.

3 METHODS

In this section, methods used in this research are

explained. We first derive the Weighted Naïve

Bayes method, and then describe three heuristics for

feature weight assignment.

3.1 Weighted Naïve Bayes (WNB)

Although similar Weighted Naïve Bayes formulas

are given by Zhang and Sheng, (2004) and Hall

(2007), we will present a complete derivation.

Standard Naïve Bayes derivation can be obtained

by placing a special form of multivariate normal

distribution, as the likelihood estimate in the famous

Bayes theorem. By special form of multivariate

normal distribution we mean that the off-diagonal

elements of the covariance matrix estimate are

assumed to be zero, i.e. the features are independent.

In this case the multivariate distribution can be

written as the product of univariate normal

distributions of each feature.

Bayes theorem states that the posterior

distribution of a sample is proportional to the prior

distribution and the likelihood of the given sample

(Alpaydın, 2004). Formally:

)(

)()|(

)|(

CPCxP

xCP

(1)

In Equation 1, the denominator is referred to as

the evidence and given by:

∑

CPCxPxP )()|()(

(2)

Evidence is a normalization constant for all classes,

thus it can be safely discarded. Then Equation 1

becomes:

)()|()|(

iii

CPCxPxCP =

(3)

In a classification problem we compute the

posterior probabilities P(C

|x) for each class and

choose the one with the highest posterior. In general

the logarithms are used for computational

convenience, which yields Equation 4.

SOFTWARE DEFECT PREDICTION: HEURISTICS FOR WEIGHTED NAÏVE BAYES

245

))(log())|(log()(

iii

CPCxPxg +=

(4)

Placing the special form of multivariate normal

distribution as explained before gives the standard

Naïve Bayes formula as given in Equation 5.

))(log(

)(

xg +

⎟

⎠

⎞

⎜

⎝

⎛

−

−=

∑

(5)

If we update Equation 3 as in Equation 6 in order to

introduce weights,

)()|()|(

CPCxPxCP

(6)

the Weighted Naïve Bayes estimator is obtained as

given in Equation 7:

))(log(

)(

wxg +

⎟

⎠

⎞

⎜

⎝

⎛

−

−=

∑

(7)

3.2 Feature Weight Assignment (WA)

3.2.1 Heuristic 1 (H1): GainRatio based WA

GainRatio is mainly used in decision tree

construction to determine the features that best splits

the data (Quinlan, 1993). Zhang and Sheng (2004)

use this heuristic for feature weight assignment. The

weight of a feature w

, where d=1..D and D is the

number of features, is given by Equation 8 (Zhang

and Sheng, 2004).

∑

)(

iGainRatio

ndGainRatio

(8)

3.2.2 Heuristic 2 (H2): InfoGain based WA

InfoGain is another method for decision tree

(Quinlan, 1993). It is also used in other studies for

feature ranking (Mladenic and Grobelnik, 1999;

Menzies, 2007). Our goal is to convert these ranking

estimates into feature weights. Therefore, we

propose the heuristic given in Equation 9.

∑

)(

iInfoGain

ndInfoGain

(9)

3.2.3 Heuristic 3 (H3): PCA based WA

PCA projects the data points onto orthogonal

principal axes such that the variance in each axis is

maximized. We claim that features with higher

weights for determining principal components

should have higher weights in the prediction

algorithm. In our proposed heuristic, we use k

eigenvalue and eigenvector pairs that correspond to

the 95% of the proportion of variance explained.

Eigenvalues are written as λ

, λ

, .., λ

. Eigenvectors

are written as e

where i=1..k, d=1..D and D is the

number of features. Then the weight of feature d is

estimated as a weighted sum of the corresponding

eigenvector elements as given in Equation 8.

∑

idi

(10)

The weights are then scaled to lie in the [0, 1]

interval by dividing each weight by the maximum

one.

4 EXPERIMENTS AND RESULTS

We have evaluated 8 public datasets (real software

applications) obtained from NASA MDP Repository

in our experiments (Nasa, 2007) (See Table 1).

Sample sizes of the projects vary from 125 to 5589

modules, which enables experiments in a range of

both small and large datasets. Each dataset has 38

features representing static code attributes. Modules

with error counts greater than zero are assumed to be

defective.

We have used probability of detection (pd) and

probability of false alarm (pf) as the performance

measures following the research by Menzies et.al.

(2007). Formal definitions for these performance

criteria are given in Equations 11 and 12

respectively and they are derived from the confusion

matrix given in Table 2. pd is a measure of accuracy

for correctly detecting the defective modules.

Therefore, higher pd's are desired. pf is a measure

for false alarms and it is an error measure for

incorrectly detecting the non-defective modules. pf

is desired to have low values. Since we need to

optimize two parameters, pd and pf, a third

performance measure called balance is used to

choose the optimal (pd, pf) pairs. balance is defined

as the normalized Euclidean distance from the

desired point (0,1) to (pd, pf) in a ROC curve

(Menzies et.al., 2007).

We have compared the standard Naïve Bayes

classifier with the three Weighted Naïve Bayes

ICSOFT 2007 - International Conference on Software and Data Technologies

246

classifiers constructed by using the three heuristics

described in Section 3. We have also reproduced the

experiments that are reported in Menzies et.al.

(2007) for comparison.

Table 1: Datasets from NASA Repository.

Name

Features

#Modules DefectRate(%)

CM1 38 505 9

PC1 38 1107 6

PC2 38 5589 0.6

PC3 38 1563 10

PC4 38 1458 12

KC3 38 458 9

KC4 38 125 4

MW1 38 403 9

We have used 10-fold cross-validation in all

experiments. That is, datasets are divided into 10

bins, 9 bins are used for training and 1 bin is used

for testing. Repeating these 10 folds ensures that

each bin is used for training and testing while

minimizing the sampling bias. Each holdout

experiment is also repeated 10 times and in each

repetition the datasets are randomized to overcome

any ordering effect and to achieve reliable statistics.

To summarize, we have performed 10x10=100

experiments for each dataset and our reported results

are the mean and standard deviations of these 100

experiments for each dataset. We have applied t-test

with α=0.05 in order to determine the statistical

significance of results. All implementations are done

in MATLAB environment. Mean results of 100

experiments for each dataset are tabulated in Table

3. Statistically significant results are indicated in

bold face.

Table 2: Confusion Matrix.

Estimated

Real Defective Non-defective

Defective A C

Non-defective B D

pd = (A) / (A+C) (11)

pf = (B) / (B+D) (12)

First thing to notice is that the standard Naïve

Bayes and PCA based heuristic are outperformed by

other methods. Both methods show statistically

significantly worse performances than others in all

datasets. They also perform similar behaviours to

each other. From this observation, we conclude that

Naïve Bayes is innately capable of discovering the

linear relative importance of features, i.e. lesser

weighted features already contribute less to the

computation of posterior probabilities.

Other heuristics based on InfoGain and

GainRatio estimates feature weights in a nonlinear

fashion. In 3 cases (PC1, PC3, KC3), they perform

equivalently and they are statistically significantly

better than other methods. In other 3 datasets (PC2,

KC4, MW1) there is no statistical difference

between the performances of these heuristics and

IG+NB. In one case (PC4) our proposed heuristic

based on InfoGain outperforms all other methods.

This is also the case for IG+NB in one case (CM1).

InfoGain and GainRatio heuristics achieve

higher pd and pf values compared to IG+NB. We

argue that the projects that require high reliability

should have higher pd values. The datasets in this

research come from NASA’s critical systems.

Therefore, InfoGain and GainRatio based heuristics

may be preferred over IG+NB.

Table 3: Results of 10x10=100 hold-out experiments.

WNB+H1 (%) WNB+H2 (%) WNB+H3 (%) NB (%) IG+NB (%)

Data

pd pf bal pd pf bal pd Pf Bal pd pf bal pd pf Bal

CM1 82 39 70 82 39 70 51 50 50 48 46 51 83 32

PC1 69 35

69 35

41 38 51 41 38 51 40 12 57

PC2 72 15

66 20 72 31 27 47 30 26 47 72 15

PC3 80 35

81 35

46 41 52 46 40 52 60 15 70

PC4 88 27 79 87 24

43 35 52 43 35 52 92 29 78

KC3 80 27

83 30

45 38 53 41 35 52 48 15 62

KC4 77 35

78 35

60 57 51 57 53 52 79 33

MW1 70 38

68 34

54 51 51 42 40 51 44 07

Avg: 77 31 72 77 32 72 46 42 51 44 39 51 65 20 61

SOFTWARE DEFECT PREDICTION: HEURISTICS FOR WEIGHTED NAÏVE BAYES

247

Overall evaluation yields 6 wins for InfoGain

and GainRatio heuristics and 4 wins for IG+NB.

These results indicate that our approach yields

comparable and in some occasions better results than

the ones reported on these datasets so far. Let us use

a simple ranking scheme for comparing these

methods: Distribute 3 points (since it is the

maximum number of concurrent winners) evenly

among winners in each case, i.e. 3 points to single

winner, 1.5 points for each in two winners case, and

1 point for each in three winners case. Then our

InfoGain based heuristic receives 9.5 points,

GainRatio based heuristic receives 8 points and

IG+NB receives 6.5 points.

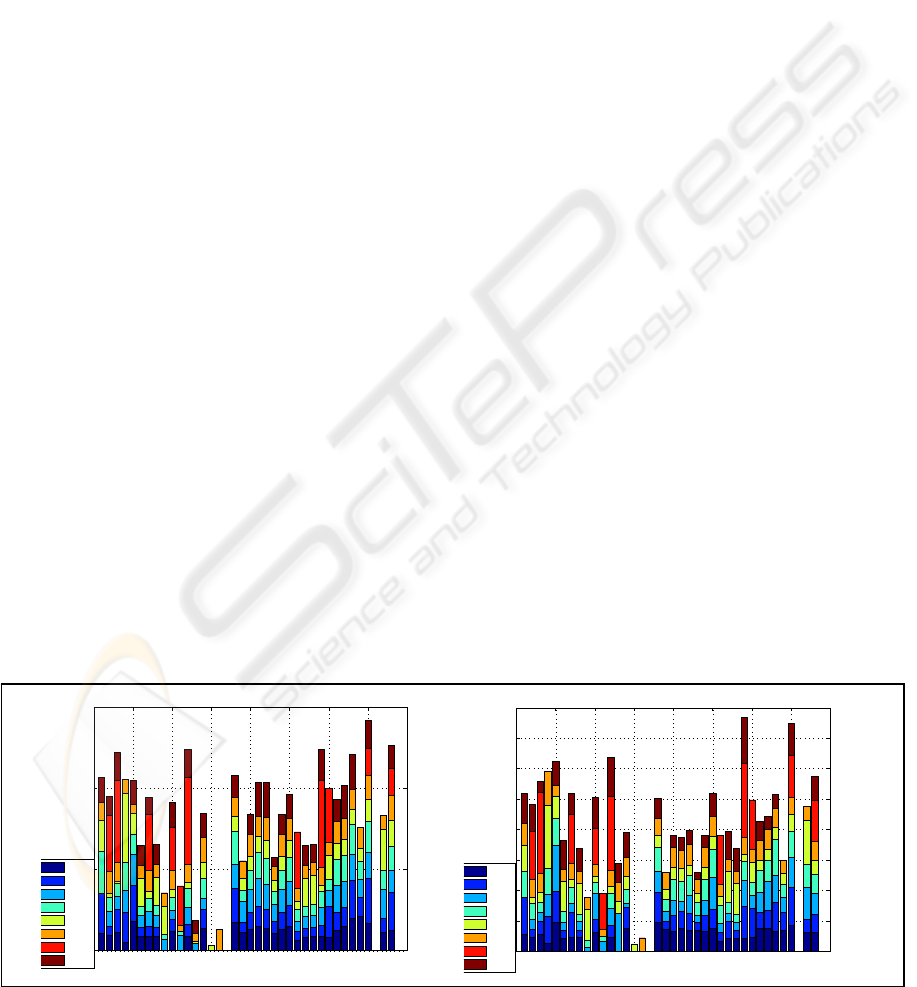
In Figure 1, we have plotted the relative weights

of 38 metrics available in the datasets. Figure 1

shows the cumulative metric weight sums over 8

datasets. The plot on the left shows these values for

InfoGain based heuristic and the plot on the right

plots values for GainRatio based heuristic.

Examining Figure 1, we see that metrics enumerated

with 17 and 36 are never used. These metrics are

‘Global Data Density’ and ‘Pathological

Complexity’. (For a complete list of metrics, see

(Nasa, 2007). An analysis of datasets shows that

these metrics have a unique value for all modules for

most of the datasets. Thus, they do not have any

discriminative power and they are eliminated. Also

metrics enumerated with 15 and 16 (‘Parameter

Count’ and ‘Global Data Complexity’) are used only

in PC4 and KC3 where similar observations are

valid. The general trend of weight assignment by

both heuristics is similar. Metrics enumerated by 3,

12, 29, 33, 35 ,38 which are ‘Call Pairs’, ‘Edge

Count’, ‘Node Count’, ‘Number of Unique

Operands’, ‘Total Number of Lines’ and ‘Total

Number of Line of Code’ respectively, are

consistently selected by these heuristics. This

collective set of software metrics are in total

accordance with the ones that Menzies et. al. (2007)

reported for subset selection.

5 CONCLUSIONS

This paper presented an application of defect

prediction built on weighted features. We have used

three heuristics in order to estimate the weights of

features based on their relative importance. Two

novel heuristics are introduced for this purpose. We

have evaluated our approach on Weighted Naïve

Bayes predictor, which is an extension of standard

Naïve Bayes. To the best of our knowledge, the

weighted features approach is a novel one in defect

prediction literature. We observed linear methods for

feature weighting lack the ability to improve the

performance of Naïve Bayes, while non-linear ones

give promising results. Our results indicated that the

proposed approach may produce statistically

significantly better results for defect prediction.

From a software practitioner’s point of view,

these results may be useful for detecting defects

before proceeding to the test phase. Additionally,

many companies in the software market develop

their standards or make use of the best practices

from industry, to determine the thresholds for

software metrics in order to guide developers during

implementation. Weights related to these metrics can

be investigated for sensitivity analysis. Our results

indicate that the impact of changes in software

metrics, to the defect rate of the final product should

vary for different metrics. Since many software

metrics are in different scales, such an analysis can

establish units of change for these metrics. All these

ideas can be implemented as a tool that performs the

mentioned analysis and offers recommendations to

developers for overall quality.

0 5 10 15 20 25 30 35 40

Enumerated Metrics

Cumilative GainRatio Feature Weights

GainRatio Weights

CM1

PC1

PC2

PC3

PC4

KC1

KC3

MW1

0 5 10 15 20 25 30 35 40

Enumerated Metrics

Cumilative InfoGain Feature Weights

InfoGain Weights

CM1

PC1

PC2

PC3

PC4

KC1

KC3

MW1

Figure 1: Metric weights.

ICSOFT 2007 - International Conference on Software and Data Technologies

248

ACKNOWLEDGEMENTS

This research is supported in part by Bogazici

University research fund under grant number BAP-

06HA104.

REFERENCES

Alpaydin, E., “Introduction to Machine Learning.”, The

MIT Press, October 2004.

Auer, M., Trendowicz, A., Graser, B., Haunschmid, E. and

Biffl, S., “Optimal Project Feature Weights in

Analogy Based Cost Estimation: Improvement and

Limitations”, IEEE Transactions on Software

Engineering., 32(2), 2006, pp. 83-92.

Basili, V. R., Briand, L. C., and Melo, W. L., “A

Validation of Object-Oriented Design Metrics as

Quality Indicators”, IEEE Transactions on Software

Engineering, 22(10), 1996, pp. 751-761.

Domingos, P. and Pazzani, M., “On the Optimality of the

Simple Bayesian Classifier under Zero-One Loss”,

Machine Learning., 29(2-3), 1997, pp. 103-130.

Fenton, N.E. and Neil, M., “A critique of software defect

prediction models”, IEEE Transactions. on Software.

Engineering., 25(5), 1999, pp. 675–689.

Fenton, N. and Ohlsson, N., “Quantitative Analysis of

Faults and Failures in a Complex Software System,” ,

IEEE Transactions on Software Engineering., 2000,

pp. 797-814.

Frank, E., Hall, M., Pfahringer, B., “Locally weighted

naive Bayes”, In Proceedings of the Uncertainty in

Artificial Intelligence Conference, Acapulco, Mexico,

Morgan Kaufmann, 2003, pp. 249-256.

Hall, M., “A decision tree-based attribute weighting filter

for naive Bayes”, Knowledge-Based Systems., 20(2),

2007, pp. 120-126.

Harrold, M. J., “Testing: a roadmap”, In Proceedings of

the Conference on the Future of Software Engineering,

ACM Press, New York, NY, 2000, pp. 61-72.

Khoshgoftaar, T. M. and Seliya, N., “Fault Prediction

Modeling for Software Quality Estimation: Comparing

Commonly Used Techniques”, Empirical Software

Engineering., 8(3), 2003, pp. 255-283.

Lewis, D. D., “Naive (Bayes) at Forty: The Independence

Assumption in Information Retrieval”, In Proceedings

of the 10th European Conference on Machine

Learning, C. Nedellec and C. Rouveirol, Eds. Lecture

Notes In Computer Science, vol. 1398. Springer-

Verlag, London, 1998, pp. 4-15.

Menzies, T., Stefano, J. D., Chapman, M., “Learning Early

Lifecycle IV and V Quality Indicators,” In

Proceedings of the IEEE Software Metrics

Symposium, 2003.

Menzies, T., DiStefano, J., Orrego, A., Chapman, R.,

“Assessing Predictors of Software Defects,” In

Proceedings of Workshop Predictive Software

Models, 2004.

Menzies T., Greenwald, J., Frank, A., “Data mining static

code attributes to learn defect predictors”, IEEE

Transactions on Software Engineering, 33(1), 2007,

pp. 2–13.

Mladenic, D. and Grobelnik, M., “Feature Selection for

Unbalanced Class Distribution and Naive Bayes”, In

Proceedings of the Sixteenth international Conference

on Machine Learning, I. Bratko and S. Dzeroski, Eds.

Morgan Kaufmann Publishers, San Francisco, CA,

1999, pp. 258-267.

Munson, J. and Khoshgoftaar, T. M., “Regression

modelling of software quality: empirical

investigation”, Journal of Electronic Materials., 19(6),

1990, pp. 106-114.

Munson, J. and Khoshgoftaar, T. M., “The Detection of

Fault-Prone Programs”, IEEE Transactions on

Software Engineering., 18(5), 1992, pp. 423-433.

Nagappan N., Williams, L., Osborne, J., Vouk, M.,

Abrahamsson, P., “Providing Test Quality Feedback

Using Static Source Code and Automatic Test Suite

Metrics”, International Symposium on Software

Reliability Engineering, 2005.

Nasa/Wvu IV&V Facility, Metrics Data Program,

available from http://mdp.ivv.nasa.gov; Internet;

accessed 2007.

Padberg, F., Ragg T., Schoknecht R., “Using machine

learning for estimating the defect content after an

inspection”, IEEE Transactions on Software

Engineering, 30(1), 2004, pp: 17- 28.

Quinlan, J. R. “C4.5: Programs for Machine Learning.”,

Morgan Kaufmann, San Mateo, CA, 1993.

Shepperd, M. and Ince D., “A Critique of Three Metrics,”

Journal of Systems and Software., 26(3), 1994, pp.

197-210.

Song, O., Shepperd, M., Cartwright, M., Mair, C.,

"Software Defect Association Mining and Defect

Correction Effort Prediction," IEEE Transactions on

Software Engineering., 32(2), 2006, pp. 69-82.

Tahat, B. V., Korel B., Bader, A., "Requirement-Based

Automated Black-Box Test Generation", In

Proceedings of 25th Annual International Computer

Software and Applications Conference, Chicago,

Illinois, 2001, pp. 489-495.

Zhang, H. and Sheng S., “Learning weighted naive Bayes

with accurate ranking”, In Proceedings of the

IEEE International Conference on Data Mining,

1(4), 2004, pp. 567- 570

Zheng, Z. and Webb, G. I., “Lazy Learning of Bayesian

Rules”, Machine Learning., 41(1), 2000, pp. 53-84..

SOFTWARE DEFECT PREDICTION: HEURISTICS FOR WEIGHTED NAÏVE BAYES

249