
MULTI OBJECTIVE ANALYSIS FOR TIMEBOXING MODELS
OF SOFTWARE DEVELOPMENT
Vassilis C. Gerogiannis and Pandelis G. Ipsilandis
Department of Project Management, Technological Education Institute of Larissa, Larissa, Greece
Keywords: Software Project Management, Iterative Development, Timeboxing, Project Scheduling, Linear
Programming, Multi-Objective Optimization.
Abstract: In iterative/incremental software development, software deliverables are built in iterations - each iteration
providing parts of the required software functionality. To better manage and monitor resources, plan and
deliverables, iterations are usually performed during specific time periods, so called “time boxes”. Each
time box is further divided into a sequence of stages and a dedicated development team is assigned to each
stage. Iterations can be performed in parallel to reduce the project completion time by exploiting a
“pipelining” concept, that is, when a team completes the tasks of a stage, it hands over the intermediate
deliverables to the team executing the next stage and then starts executing the same stage in the next
iteration. In this paper, we address the problem of optimizing the schedule of a software project that follows
an iterative, timeboxing process model. A multi objective linear programming technique is introduced to
consider multiple parameters, such as the project duration, the work discontinuities of development teams in
successive iterations and the release (delivery) time of software deliverables. The proposed model can be
used to generate alternative project plans based on the relative importance of these parameters.
1 INTRODUCTION
In iterative and incremental development, software
is built gradually by following a sequence of
iterations, with each of the iterations delivering a
part of the final software system (Larman, 2003). A
common project management technique that has
been associated with iterative/incremental software
processes (e.g., Rational Unified Process - RUP,
Dynamic Systems Development Method - DSDM) is
timeboxing (Hunt, 2003; Stapleton, 2003). In
timeboxing, iterations are performed during specific
time periods, so called “time boxes”. The
timeboxing model is suitable for software
development projects in which delivery times are
crucial and system requirements are stable or, at
least, they can be grouped into classes of features to
be developed during different time boxes/iterations.
The main objective of timeboxing is to deliver
the final software system as quickly as possible and
avoid risks of missing project deadlines (Jalote et
al., 2004). Each time box is divided into a sequence
of stages (e.g., requirements analysis, design,
implementation, testing and deployment) that are
repeated in each time box (Figure 1). A dedicated
team of experts is usually assigned to each stage,
i.e., a team for a stage performs only the activities
for that stage. Iterations in timeboxing can be
performed in parallel to further improve the project
performance and reduce the overall project duration.
Parallelism is achieved by exploiting a “pipelining”
concept from hardware architectures (Hennesy and
Patterson, 2004), that is, when a team completes the
tasks of a stage, it hands over the intermediate
deliverables to another team executing the next stage
and then starts executing the same stage in the next
timeboxed iteration.
However, the application of a timeboxing process
model is often associated with some “inherent”
assumptions/simplifications which require proper
configuration/resource management procedures
(Jalote et al., 2004):
the number and duration of time boxes are fixed,
the planned durations of each stage, in each time
box, are approximately equal,
precedence constraints between stages, in each
iteration, are simple sequential relationships,
145
C. Gerogiannis V. and G. Ipsilandis P. (2007).
MULTI OBJECTIVE ANALYSIS FOR TIMEBOXING MODELS OF SOFTWARE DEVELOPMENT.
In Proceedings of the Second International Conference on Software and Data Technologies - Volume ISDM/WsEHST/DC, pages 145-153
DOI: 10.5220/0001341501450153
Copyright
c
SciTePress
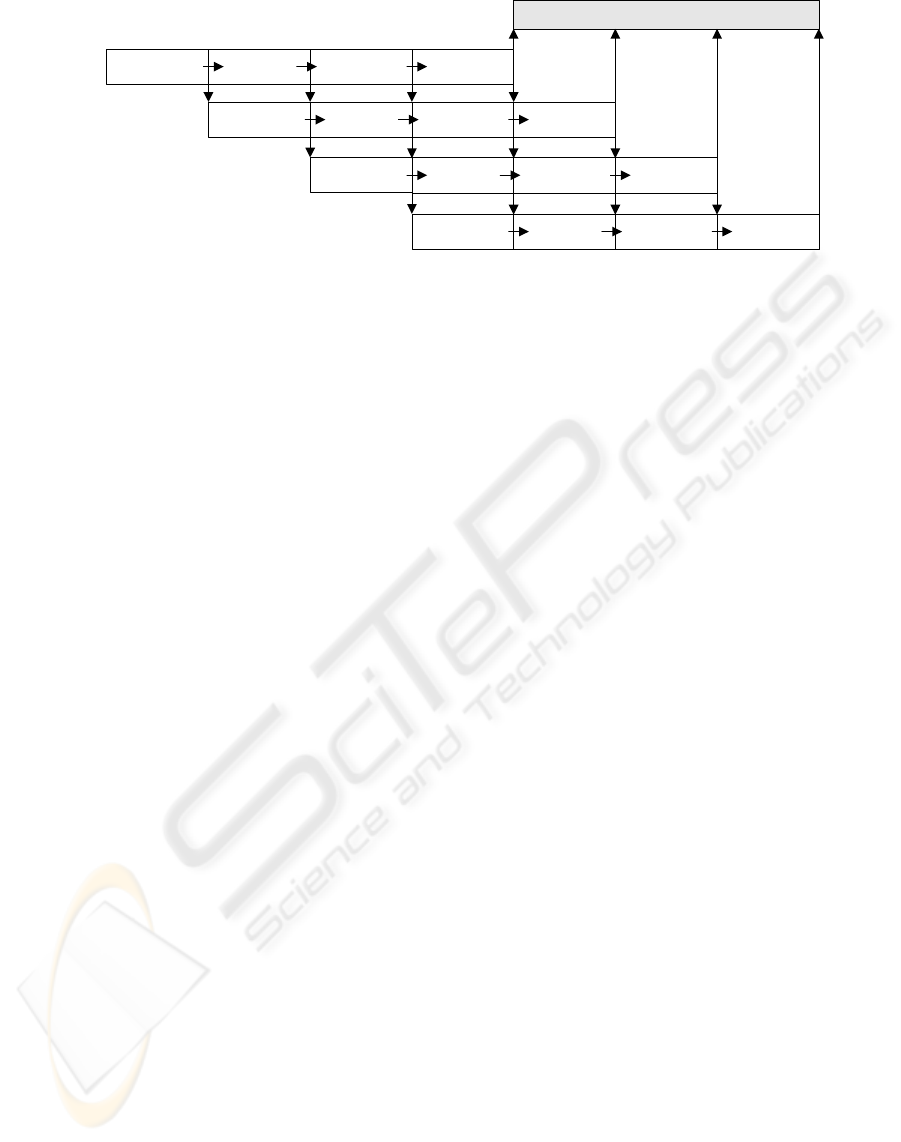
TimeBox1
TimeBox2
TimeBox3
TimeBox4
Requirements Design
Impementation
Testing &
Deployment
Requirements Design
Impementation
Testing &
Deployment
Requirements Design
Impementation
Testing &
Deployment
Software System
Requirements Design
Impementation
Testing &
Deployment
Figure 1: The timeboxing process model.
requirements, system architecture and
technology are considered as quite stable to be
managed separately into different time
boxes/iterations,
development teams, performing the same type of
activity at respective stages in different
timeboxed iterations, should be experienced and
“coherent” enough to ensure high resource
utilization and avoid idle times/work
discontinuities in successive iterations.
A serious drawback of timeboxing is that possible
work discontinuities affecting the project velocity
(XP, 2006) cannot be easily handled. For example,
even with a highly experienced team of designers,
execution of activities in the corresponding stage of
a particular time box/iteration cannot be performed
“immediately” after the same (or a different) team
has completed the activities of the design stage in
the previous time box. In reality, due to the different
scope of the design activities (database system
design, user interface design etc.), software projects
require larger amount of resources (e.g., multi-
disciplined designers), thus raising coordination
issues, transition/communication delays and
resource time losses between design stages in
successive iterations. Consequently, there is a
learning curve associated with any team to become
familiar with the features to be implemented at each
stage and the corresponding user requirements
(Hanakawa et al., 1998). Furthermore, in a multi site
software development project (Ebert and De Neve,
2001), members of development teams may be
drawn from several locations, thus introducing
additional communication gaps/coordination delays.
Even when the system architecture is quite fixed
(e.g., in a software project developing a web
application), the set of features to be considered
during the design stage of a specific iteration
depends on the outcomes of the previous
requirements stage and any new requirements
introduced by the end-user. In such cases, the
development of a software project based on a “rigid”
timeboxing approach is getting much more complex
and should be supported with more systematic and
holistic methodologies that address diverse
scheduling decision elements, regarding the overall
project performance.
This paper, contributes to further promote the
applicability of the timeboxing process model in
software projects that require more effective
resource management and planning, by exploring the
multi objective approach in planning and scheduling
decisions. In particular, we propose a multi objective
linear programming (LP) model for scheduling
projects which employ timeboxing (TB projects).
The model includes a list of criteria (such as project
duration, iteration completion/release time of
software increments and work gaps), which are
important for TB project managers in making
decisions regarding the overall project performance.
Thus, the scheduling problem of TB projects is
regarded as a multi criteria decision that can be
formulated by linear programming techniques. Such
a Multi Criteria Decision Analysis (MCDA)
approach is based on a parametric objective function
which, according to the values of its parameters,
aims either at a single criterion optimization or at a
multi-objective optimization, by combining different
criteria into a single cost criterion for the whole
project.
The rest of the paper is organized as follows:
Section 2 describes the background of our approach.
Section 3 presents a formal linear programming
formulation for scheduling TB software projects.
Section 4 presents the application of the model to a
software project example that follows practices of
iterative/timeboxed planning as well as the project
schedule evaluation under individual criteria.
Section 5 presents the project schedule evaluation by
considering multiple criteria; the model utilization to
assist software project managers in selecting among
alternative project schedules is also discussed.
ICSOFT 2007 - International Conference on Software and Data Technologies
146

Finally, conclusions and directions of future research
are discussed in section 6.
2 BACKGROUND
While MCDA approaches have been applied in other
fields of software engineering and software project
management, there is a lack of attention to the
problem of efficiently scheduling iterative software
development, in general, and TB projects, in
particular. For example, in (Lai et al., 2002;
Santhanam and Kyparisis, 1995) MCDA techniques
have been proposed to assist the problem of
selecting a software development project from a set
of projects by considering the cost of the respective
investment; in (Wang and Lin, 2003; Ruhe et al.,
2003) MCDA techniques have been suggested to
select and prioritise software requirements; in
(Stamelos and Tsoukias, 2003) a multi criteria
model has been applied to evaluate the software
quality; while in (Barcus and Montibeller, 2006)
MCDA has been employed to support work
allocation in distributed software development
teams.
With regard to TB project scheduling, Jalote et
al., (2004) examine the cost of unequal stages to the
overall performance and resource utilization of a TB
project. In their paper, the pipelining concept from
hardware architectures is exploited to provide a
process model for TB projects and, consequently, to
determine the overall project duration, in case that
time boxes are decomposed into unequal stages.
Each stage is considered equal to the longest stage;
the frequency of deliverables produced (i.e., the
project velocity), as well as the project duration are
determined by the longest stage. The model
application results in “slack time” for the teams
performing the “slower” stages (i.e., resources
under-utilization). The problem is handled in an ad-
hoc way by reducing the size of teams for the slower
stages. In addition, the suggested approach assumes
a simplified nature for TB projects where: i) the
number/duration of timeboxes/stages is fixed and
pre-specified, ii) there are no transition delays (work
gaps) between stages in successive iterations, and
iii) in each timeboxed iteration, stages proceed at a
sequential manner. Hence, the model does not take
into account multiple decision elements for
scheduling TB projects, such as the project duration,
the completion time of each iteration that determines
the time of the next software release increment,
possible precedence relationships due to
technological constraints between stages, as well as
transition delays/work discontinuities between
stages in successive iterations.
To alleviate the above limitations, in this paper
we try to exploit recent advances of MCDA in other
project management areas which exhibit analogous
characteristics to TB software projects. For example,
many instances of construction engineering projects
consist of a set of activities that are repeated at
different locations/units (Mattila and Abraham,
1998). After an activity is completed in one site, it is
repeated in the next site either at a horizontal
(highway segments, railways bridges, tunnels,
pipelines, sewers etc.) or a vertical flow (high-rise
and multi-story buildings, multi-housing projects,
etc.) These projects are known in the construction
engineering literature as Linear and Repetitive
Projects (LRPs) (Hassanein and Moselhi, 2005).
Scheduling of LRPs, in practice, could involve
multiple control variables than just minimizing the
project duration or achieving resource continuity,
which are the objectives in conventional project
scheduling techniques like PERT/CPM and RSM
(Repetitive Scheduling Method), respectively
(Kallantzis and Lambropoulos, 2004; Yang and
Ioannou, 2004). Alternative project schedules,
comparisons and cost trade-offs are often required to
arrive at an acceptable or optimum project schedule.
In this aspect, the scheduling problem in LRPs has
been recently considered as a multi objective
problem that can be addressed by linear
programming techniques (Hassanein and Moselhi,
2005; Hyari and El-Rayes, 2006; Ipsilandis, 2007).
In the following, a multi objective linear
programming scheduling model, originally defined
for LRPs (Ipsilandis, 2007), is adapted to schedule
software projects which employ timeboxing. The
model has the capacity to provide optimum
schedules, reflecting not only single but multiple
objectives, and assist software project managers in
producing and selecting among alternative schedules
of a TB project.
3 THE MULTI OBJECTIVE
NATURE OF TB PROJECTS
In a TB project, a list of criteria important to the
software project manager in his/her decision making
regarding the overall project performance may
include the following:
Project duration.
Resource idle time: in TB projects, work gaps
between stages in successive timeboxed
MULTI OBJECTIVE ANALYSIS FOR TIMEBOXING MODELS OF SOFTWARE DEVELOPMENT
147

iterations cannot be ignored. Although the same
stage is repeated sequentially in different
timeboxes, violating the continuity of the same
stage between successive timeboxes introduces
work gaps and time losses that increase the
overall project cost and duration.
Iteration completion time: The completion of
each iteration and, consequently, the time of the
next software release increment are affected by
the precedence relationships/technological
constraints between stages and the duration of
each stage. The iteration completion time
identifies a proper choice/milestone (i.e., a
minimum bound) for the duration of the
corresponding time box and, thus, specifies the
iteration deadline. The project manager can then
identify the amount of functionality to be
developed at each iteration, that is, the
functionality that can be “fit” into a time box.
Iterations result in some working software
released to the customer for early feedback or to
the Quality Assurance team. The final iteration
results in the final software product.
Slack time: Reducing a stage slack time may
result in achieving a high level of work
continuity and resource utilization but, at the
same time, introduces higher risk, regarding the
completion time of iterations and the overall
project duration.
Number of iterations: A TB project requires a
good estimation of the software features to be
developed and released after each iteration. We
assume that each iteration introduces an
additional fixed cost for the project but, at the
same time, splits the software system into
smaller parts which could improve the overall
cash flow and keep management complexity
under control.
In any TB project, there is a set of M stages and P
project dependency relationships (with or without
time-lag). The project is divided into N separate
iterations in a “linear” way, where, without loss of
generality, the following assumptions hold: i) all
stages are performed in all iterations, ii) a stage
cannot be performed in any iteration before the same
stage is completed in the previous iteration, and iii)
the set of precedence dependencies remain the same
in all iterations (i.e., the same planning method is
followed in all iterations).
Let i = 1,2,…,M denote the project stages and
j = 1,2,…,N denote the project iterations. Scheduling
of a TB project can be formulated as a linear
programming model as follows.
Model Variable and Parameters.
Define:
d
ij
, the duration of stage i in iteration j,
s
ij
, f
ij
, the start and finish time respectively of
stage i in iteration j,
l
ij
, the minimum elapsed time for starting stage
i in iteration j+1, after finishing stage i in iteration j,
P
i
, the set of predecessor stages to stage i,
E , the set of all stages without successors,
WB
i
, the total duration of work-breaks for stage i
because of discontinuities in successive iterations,
UC
j
, the completion time of iteration j,
D
j
, the promised delivery/release time for the
software part produced in iteration j,
c
j
, the unit cost of delay in finishing iteration j
after the deadline (timebox),
f
i
, the unit cost of work-breaks in stage i.
Constraint definitions.
Define:
Stage duration constraints:
f
ij
= s
ij
+ d
ij
∀
i=1, 2…M, j=1, 2… N (1)
Project linearity constraints:
s
ij+1
≥ f
ij
+ l
ij
∀
i=1, 2… M, j=1, 2… N-1 (2)
When l
ij
= 0, the constraint takes the form of the
common finish-to-start relationship.
Technological dependencies:
s
ij
≥ f
kj
∀
i=1, 2… M, j=1, 2…N, k
∈
P
i
(3)
Iteration completion time:
UC
j
≥ f
kj
∀
j=1,2…N, k
∈
E (4)
UC
j
is the completion time for iteration j and UC
N
is
equal to the project duration.
Resource delays (work-breaks):
)
N-1
i
ij+1 ij
j=1
= (s f , i = 1,...,M
WB
−∀
∑
M
i
i=1
=WB
WB
∑
(5)
Global Objective function.
Depending on the values of the parameters c
j
and f
i
the following general objective function:
Minimize
.( ) .
NM
j
jj ii
j=1 i=1
cUC D fWB−+
∑∑
(6)
can be used accordingly, to achieve different
objectives or for trade-offs between various criteria,
as follows:
Project duration (c
N
=1, rest of c
j
and f
i
equal to 0):
MinimizeUC
N
(7)
Total work-break time (all f
i
= 1, all c
j
= 0):
Minimize WB (8)
Iteration completion time (all f
i
= 0, c
j
= 1):
ICSOFT 2007 - International Conference on Software and Data Technologies
148
Minimize
M
i
i=1
UC
∑
(9)
Total cost of work-breaks (all c
j
= 0):
Minimize
.
M
ii
i=1
f
WB
∑
(10)
Delay cost (all f
i
= 0):
Minimize
.( )
M|
j
jj
i=1
cUC D−
∑
(11)
Trade-offs between costs of project delays and
resource delays (work-breaks):
Minimize
.( ) .
NM
j
jj ii
j=1 i=1
cUC D fWB−+
∑∑
(12)
4 CASE-STUDY EXAMPLE
In this section, we demonstrate the type of answers
and analysis that can be supported by the proposed
model through the use of a hypothetical short-term
software project example that follows the principles
of the agile ICONIX process (Rosenberg et al.
2005). In ICONIX, the project processes are use-
case driven, like in RUP, but without a lot of the
project management overhead that the RUP
introduces. The project example follows a minimal
set of 6 stages/steps which are executed in an
iterative/incremental approach. These stages are:
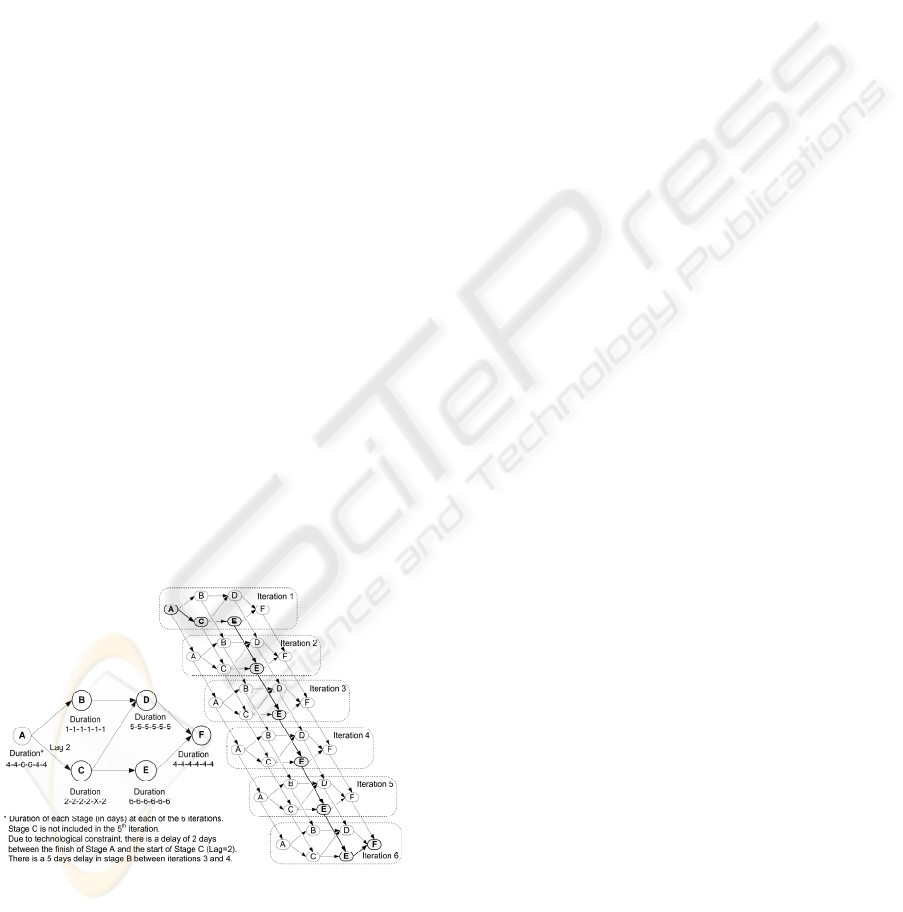
Domain Modelling (stage A), Use-Cases Analysis
(stage B), Requirements Review (stage C),
Preliminary Design & Review (stage D), Detailed
Design & Review (stage F) and Coding & Testing
(stage F).
Figure 2: Precedence and PERT network.
Multiple iterations occur between developing the
domain model (stage A) and analyzing the use cases
(stage B). Other iterations exist, as well, as the
development proceeds through the project life cycle.
Although the project does not require a lot of
bookkeeping, in order to over-utilize the small
development teams working at each stage (2-3
experts), all iterations should be somehow
“timeboxed”.
The final software application is
planned to be delivered after 6 iterations, of the 6
discrete stages specified above. A stage-specific
development team executes the activities at the
corresponding stage following the sequence of
iterations. All stage dependencies are finish-to-start
(FS), as shown in the precedence network diagram
on the left of Figure 2 along with the most likely
estimate of the duration of each stage at each of the
6 iterations. The network also depicts precedence
constraints between stages within iterations (e.g.,
Use-Cases Analysis and Requirements Review
stages take place in parallel after Domain Modelling
is completed).
Although the initial objective was to keep project
management complexities as low as possible, the
resulting PERT diagram for all six iterations
portrays a multiplicative complexity for the whole
project (Figure 2). The critical path of the entire
project consists of stages A and C in iteration 1, the
sequence of stage E in all iterations, and stage F in
iteration 6.
4.1 CPM ES & LS Schedules
The schedule produced from the Critical Path Early
Start Method (CPM ES) minimizes the project
duration and, at the same time, the completion time
(the release time for software parts) in all iterations.
In general, obtaining a partial software delivery as
early as possible could affect negatively the software
quality but positively the financial performance of
the project, in cases where customer payments are
contingent upon partial deliveries. In such a case, the
objective must be set to minimizing the completion
time of all or certain iterations (that is to minimize
as much as possible the time boxes of iterations),
even if work continuity is sacrificed. Note that an
iteration completion time denotes a lower bound for
the corresponding time box.
Setting the objective function as in Eq. 9 the LP
solution coincides with the CPM ES schedule which
yields for the project example a duration equal to 48
working days, with iteration completion times and
work-breaks set as shown in Figure 3. In the
corresponding linear scheduling diagram, the
progress of each stage through the project iterations
is represented by a piecewise straight line. The slope
of the line corresponds to the production rate of the
specific stage at each iteration. Horizontal segments
MULTI OBJECTIVE ANALYSIS FOR TIMEBOXING MODELS OF SOFTWARE DEVELOPMENT
149

on the progress line correspond to work-breaks (i.e.,
work interruption) between the execution of the
same stage in successive iterations. Vertical
segments represent specific cases, where a stage is
not included in the corresponding iteration.
Figure 3: Linear scheduling (CPM - ES).
CPM is insufficient in addressing work
continuity objectives and, consequently, does not
consider utilization levels of development teams.
Work-breaks cannot be eliminated or even reduced
by scheduling stages according to the Latest Start
(LS) time, as it is demonstrated in Figure 4.
Figure 4: Linear Scheduling (CPM - LS).
Pushing stages to their LS time moves work-
breaks from the last project stages to those in the
beginning. In the specific project example, the LS
schedule introduces even more work-breaks, while,
at the same time, produces delays in
intermediate/partial deliveries (i.e., timebox
violations). Additionally, the LS schedule fails to
address planning for agility aspects (Rosenberg et al.
2005), since it consumes all the “slack time” for
teams performing the stages, hence making the
project performance more vulnerable to unexpected
delays/interrupts (e.g., major design errors, changes
in user requirements etc.).
4.2 Minimizing Work-Break Time
Setting the 48 days CPM duration as the constraint
of Eq. 4 (UC
6
=48), and selecting the objective
function of Eq. 8, the LP model produces a schedule
that minimizes the total resource work-break time,
while maintaining the overall project completion
time as set by the CPM schedule. The resulting
schedule for the project is shown in Figure 5. The
minimum project duration of 48 days can be
achieved with a minimum of 26 days of work-breaks
concentrated at stages B and C. Further reduction of
stages work-break time cannot be achieved without
extending the project duration beyond 48 days.
Figure 5: Minimization of work-breaks under CPM
duration.
If the CPM duration constraint is relaxed, work-
breaks can be further reduced to a minimum of 5
days, causing however a delay in the delivery of the
project, the duration of which is extended from 48 to
64 days, as depicted in Figure 6.
Figure 6: Minimization of work-breaks without duration
constraints.
The work-break at stage C is eliminated, while at
stage B is reduced to 5 days. The completion time of
all iterations is also pulled to 16 days later than in
the previous schedule. A saving of 21 days in work-
ICSOFT 2007 - International Conference on Software and Data Technologies
150

breaks is traded-off with a project delivery delay of
16 days. In the next section, trade-off issues between
work-breaks and software parts delivery/release
times are further investigated by using LP sensitivity
analysis.
5 TRADE-OFF ANALYSIS
All schedules derived under the previous conditions
were based on a single criterion each time.
Alternative schedules optimized with respect the
different evaluation criteria as they are defined in
Eqs. 7-11, can also be easily derived by the LP
model. The objective function defined in Eq. 12
consolidates the criteria of project duration, iteration
completion time/time box duration (release time of
each software part), and work-break into a single
composite criterion. A necessary condition is to
estimate the relative unit cost of each of the above
project parameters.
Work-break costs may vary among different
stages, according to the effort and scarceness of the
resources (team members) involved in each stage.
The same holds true with the cost associated with
delays in completion/delivery time of different
iterations (i.e., the cost of violating timebox
constraints) which can affect the overall cost of the
project, either directly (i.e., delay penalties) or
indirectly (i.e., financial cost due to late cash
receipts or delays in revenue generation). However,
the sensitivity analysis results on the parameters of
the objective function of Eq. 12 can be used to
establish optimum schedules at different levels of
cost relations, with no need to have accurate
estimates of the exact cost, as it is demonstrated in
the following two examples.
5.1 Trade-off between Project
Duration Delay and Work-Breaks
The first example demonstrates a trade-off analysis
between the cost of delays in project completion and
that of work-breaks. Delays are measured in time
units as deviations from the earliest finish date of the
project as it is set by the CPM or from any
predefined delivery date set by the project manager
and/or the final user. It is also assumed that
intermediate delays in completing individual project
iterations do not impose any additional cost to the
project, and that the cost of work-breaks is the same
for all stages. In this case, the objective function
(Eq. 12) of the model is equivalent to:
Minimize c(UC
N
) + f(WB) or
Minimize c{UC
N
+( f/c)WB} (13)
where c and f denote the daily cost of project delay
and work-break, respectively.
The results of the sensitivity analysis on the
values of the coefficient f/c of the objective function
in Eq. 13 set optimality ranges, associated with
alternative optimum schedules as shown in Figure 7.
For the specific project example three optimality
ranges are identified: When the work-break unit cost
ranges between zero and up to 50% of the delay cost
(Range I), the optimum scheduling results in project
duration of 48 days (minimum possible) with a
maximum work-break time of 26 days. When the
work-break unit cost ranges between 50% to 100%
of the delay cost (Range II), it is more economical to
let the project duration slip by 5 days in order to gain
a reduction of 16 days in work-breaks. Finally, when
the work-break cost exceeds the lateness cost (Range
III), the optimum schedule is the one that reduces
work-breaks to the minimum of 5 days, which
results in extending the project duration by 16 days.
Figure 7: Trade-off between project completion delays and
work-breaks.
5.2 Trade-off between Iteration
Completion Delays
and Work-Breaks
In the second example, we examine the scenario
where a penalty cost is associated with delivery
delays in the completion of individual project
iterations. Delivery delays/time box violations could
be measured as deviations from the earliest finish
dates of the project iterations (Figure 3) or from a
promised time box specified by the project manager
and/or the customer for each software release. The
choice does not affect at all the range analysis that
follow, since the cost coefficients of the objective
function remain unchanged. For simplicity purposes
we assume that the same penalty applies to delays in
any timeboxed iteration. Also, as in the previous
MULTI OBJECTIVE ANALYSIS FOR TIMEBOXING MODELS OF SOFTWARE DEVELOPMENT
151

case, the cost of work-breaks is assumed to be the
same for all stages. In this case, the objective
function (Eq. 12) of the LP model can be written as:
Minimize
.( ) .
NM
j
jj ii
j=1 i=1
cUC D fWB−+
∑∑
or
Minimize
(
)
⎧⎫
+−
⎨⎬
⎩⎭
∑∑∑
NMN
jij
j=1 i=1 j=1
f
cUC WBcD
c
(14)
Since the second part of Eq.14 is constant, the
analysis to define ranges of optimality is based on
the level of the f/c ratio. The results shown in Figure
8 indicate 10 optimality ranges corresponding to 10
different optimum solutions, according to the
relation of the work-break to the iteration
completion cost. A schedule which minimizes the
work-break time (5 days) is optimum only when the
associated work-break cost is at least 6 times the
cost paid for iteration delays, and it is achieved by
introducing a total of 108 days of delay in the
completion of all iterations. As the relative size of
the work-break to iteration delay cost drops,
alternative solutions that allow for work-breaks may
be more cost efficient.
Figure 8: Trade-off between iteration completion delays
and work-breaks.
A notable break point in optimality conditions
occurs at the point where work-break cost is 3 times
the cost of delays. Under this level total delays in the
iterations are kept below 18 days in total (average 3
days per iteration) while above it, delays range from
33 to 108 days (about 5,5 to 18 days per iteration).
Figure 8 gives a graphical representation of the
results. Any distinct segment of a cost coefficient
ratio defined by the sensitivity analysis, corresponds
to an optimal schedule associated with specific
project duration, delays in iteration completion and
work-breaks. The number of alternative optimum
solutions, the trade-off brake points and levels
depend on the constraints of the specific problem
that define the set of all feasible schedules.
6 CONCLUSIONS
Project scheduling in iterative software projects
which employ a timeboxing process model is
generally not a single dimension decision process. A
scheduling decision should take into account more
than a single factor and, most of the times, trade-offs
are required between iteration completion times
(violations of time boxes), project duration and
work-breaks for teams working in the same stages in
successive project iterations. In this paper, we
proposed a multi objective linear programming
model to address these issues and overcome some
simplifications of conventional timeboxing. In the
proposed model, the planning duration of iterations
is not a priori fixed, the durations of each stage in
each respective time box may be not equal,
precedence constraints between stages in each
iteration are not simple sequential relationships, and,
finally, it is possible to consider a wider range of
software projects, where work discontinuities exist
between stages in successive iterations. The model
has the capacity to provide optimum schedules for
iterative projects which follow timeboxing
disciplines, reflecting not only single but multiple
objectives and assists software project managers in
selecting among alternative schedules based on the
relative magnitude of different cost elements. In this
sense, the presented model provides software
managers with the capability to consider alternative
schedules besides those defined by minimum
duration or minimum work-break criterion.
A fully integrated software implementation of
the proposed approach in a model-based
environment that supports the graphical
representation of software development processes
and the process managerial analysis as well
(Gerogiannis et al., 2006) will enhance its
applicability to real-world software projects.
Although the model implementation, as it stands,
can handle the problem formulation of various types
of timing constraints, there are other issues that need
further research. One such issue is the formal
modeling of developers’ learning curves (Hanakawa
et al., 2002) to consider measures of software
productivity and estimates for projects progress.
Another research area that we plan to consider is the
risk level associated with the alternative scheduling
decisions, as it is indicated by the slack time of the
iteration stages and the probability of meeting the
objectives set (software delivery times, work-breaks,
etc.), since unexpected events in one stage or
iteration (e.g., major changes in user requirements)
may affect not only the duration of the project and
ICSOFT 2007 - International Conference on Software and Data Technologies
152

the iteration completion/delivery times but also the
work continuity in project resources. Similarly, the
use of simulation techniques could provide further
insight on the stability of the alternative optimum
solutions defined by the trade-off approach.
ACKNOWLEDGEMENTS
This work was partially funded by the Greek
Ministry of Education under the R&D projects
MISSION-SPM and EYPOLYS, in the context of
the ARCHIMEDES national research programme.
REFERENCES
Barcus, A., Montibeller, G., 2006. Supporting the
Allocation of Software Development Work in
Distributed Teams with Multi-Criteria Decision
Analysis. Omega International Journal of Management
Science, to be published in 2007, available at:
www.sciencedirect.com.
Ebert, C., De Neve, P., 2001. Surviving Global Software
Development. IEEE Software, 18(2), 62-69.
Gerogiannis, V.C., Kakarontzas, G., Stamelos, I., 2006. A
Unified Approach for Software Process
Representation and Analysis. In Proceedings of the 1
st
ICSOFT International Conference on Software and
Data Technologies, 127-132.
Hanakawa, N., Morisaki, S. & Matsumoto, K., 1998. A
Learning Curve Based Simulation Model for Software
Development. In Proceedings of the 20th International
Conference on Software Engineering, IEEE Comp.
Soc. Press, 350–359.
Hanakawa, N., Matsumoto, K., Torii, K., 2002. A
Knowledge-Based Software Process Simulation
Model. Annals of Software Engineering, 14(1-4), 383-
406.
Hassanein, A., Moselhi, O., 2005. Accelerating Linear
Projects. Construction Management and Economics,
23(4), 377-385.
Hennesy, J.L., Patterson, D.A., 2004. Computer
Organization and Design: the Hardware/Software
Interface. Morgan Kaufmann Publishers, 3
rd
edition.
Hunt, J., 2003. Incremental Software. In Guide to the
Unified Process Featuring UML, Java and Design
Patterns, Springer Prof. Comp., 2
nd
edition, 383-394,
available at: www.springerlink.com
Hyari, K., El-Rayes, K., 2006. Optimal Planning and
Scheduling for Repetitive Construction Projects.
Journal of Management in Engineering, 22(1), 11-19.
Ipsilandis, P.G., 2007. A Multi Objective Linear
Programming Model for Scheduling Linear Repetitive
Projects, Journal of Construction Engineering and
Management, to be published in June 2007.
Jalote, P., Palit, A., Kurien, P., Peethamber, V.T., 2004.
Timeboxing: a Process Model for Iterative Software
Development. Journal of Systems and Software, 70(1-
2), 117-127.
Kallantzis, A., Lambropoulos, S., 2004. Critical Path
Determination by Incorporation of Minimum and
Maximum Time and Distance Constraints into Linear
Scheduling. Engineering, Construction and
Architectural Management, 11(3), 211-222.
Lai, V.S., Wong, B.K., Cheung. W., 2002. Group Decision
Making in a Multiple Criteria Environment: a Case
Using the AHP in Software Selection. European
Journal of Operational Research, 137 (1), 134-144.
Larman, C., 2003. Agile and Iterative Development: A
Manager's Guide. Addison-Wesley, 1
st
edition.
Mattila, K.G., Abraham, D.M., 1998. Linear Scheduling:
Past Efforts and Future Directions. Engineering,
Construction and Architectural Management, 5(3),
294-303.
Rosenberg, D., Stephens, M., Collins-Cope, M., 2005.
Agile Development with ICONIX Process: People,
Process, and Pragmatism. A-Press.
Ruhe, G., Eberlein, A., Pfahl, D., 2003. Trade-off Analysis
for Requirements Selection. International Journal on
Software Engineering and Knowledge Engineering,
13(4), 345-366.
Santhanam, R., Kyparisis, J., 1995. A Multiple Criteria
Decision Model for Information System Project
Selection. Computers and Operations Research, 22(8),
807-818.
Stamelos, I., Tsoukias, A., 2003. Software Evaluation
Problem Situations. European Journal of Operational
Research, 145 (2), 273-286.
Stapleton, J., 2003. DSDM: Business Focused
Development. Addison-Wesley, 2
nd
edition.
Wang, J., Lin, Y-I., 2003. A Fuzzy Multicriteria Group
Decision Making Approach to Select Configuration
Items for Software Development. Fuzzy Sets and
Systems, 134(3), 343-363.
XP, 2006. Extreme Programming: a Gentle Introduction.
Available at: www.extremeprogramming.org
Yang, I. T., Ioannou, P.G., 2004. Scheduling with Focus
on Practical Concerns in Repetitive Projects.
Construction Management and Economics, 22(6), 619-
630.
MULTI OBJECTIVE ANALYSIS FOR TIMEBOXING MODELS OF SOFTWARE DEVELOPMENT
153
