COLOR IMAGE PROFILE COMPARISON AND COMPUTING

Imad El-Zakhem

a,c

, Amine A

ıt Younes

CReSTIC-MODECO, Universit

e de Reims Champagne Ardenne, rue des Cray

eres BP 1035, 51687 Reims cedex 2, France

Isis Truck

, Hanna Greige

MSH Paris-Nord, Universit

e Paris 8, 4 rue de la Croix Faron, Plaine Saint-Denis, 93210 Saint-Denis, France

University of Balamand, P.O.Box 100, Tripoli, Lebanon

Herman Akdag

LIP6, Universit

e Paris 6, 104 avenue du Pr

esident Kennedy, 75016 Paris, France

Keywords:

Colorimetric proﬁle, Color representation, Perception modeling, Fuzzy logic, Image retrieval.

Abstract:

This paper describes a method that analyzes the content of images while building their colorimetric proﬁle

as perceived by the user. First, images are being processed relying on a standard or initial set of parameters

using the fuzzy set theory and the HLS color space (Hue, Lightness, Saturation). These parameters permit to

describe and qualify the colors and their properties. Each image is processed pixel by pixel and is affected to

a detailed initial colorimetric proﬁle. Secondly, we present a method that will recalculate the amount of colors

in the image based on another set of parameters, so the colorimetric proﬁle of the image is being modiﬁed

accordingly. Avoiding the repetition of the process at the pixel level is the main target of this phase, because

reprocessing each image is time consuming and turned to be not feasible. Finally we present the software that

processes images and that recalculates their colorimetric proﬁles with some examples.

1 INTRODUCTION

Classifying images according to their colors has been

studied extensively and many methods and results

were presented (Chen and Wang, 2002) (Truck and

Akdag, 2003) (Omhover et al., 2004) (A

ıt Younes

et al., 2007). Color is deﬁned as an attribute of visual

perception consisting of any combination of chro-

matic and achromatic content. This attribute can be

described by chromatic color names such as yellow,

orange, etc., or by achromatic color names such as

white, gray, black, and qualiﬁed by bright, light, etc.,

or by combinations of such names (CIE, 1987) (Her-

rera and Mart

ınez, 2001). Truck et al. talked about

colors and their qualiﬁers (Truck and Akdag, 2003).

Deﬁning the colorimetric proﬁle of an image is not

sufﬁcient since this proﬁle is subjective and differ-

ently perceived by other user. On the other hand, a

considerable amount of time is needed to process the

images of the database, to assign new membership de-

grees to each color, and to make new colorimetric pro-

ﬁles. Our aim is to develop a method to compute the

new proﬁle based on the initial one.

2 STANDARD COLORIMETRIC

PROFILE

The main aim of this paper is to construct the appro-

priate colorimetric proﬁle for images; thus we will be

able to deﬁne the membership degree of the image I

in all perceived colors. For example we say that the

membership degree of red in the image I is 0.2, of

blue is 0.15, etc.

2.1 Chromatic Colors

The process adopted by Truck et al. consists of mod-

eling the three dimensions of color (hue, saturation

and lightness) by using fuzzy membership functions.

According to HLS space, the dimension hue varies

from 0 to 255 and consists of all perceived colors from

red to pink. We denote the set

T of the 9 fundamental

colors according to Newton by:

T = {red, orange, yellow, green, cyan, blue, pur-

ple, magenta, pink}

Each chromatic color is a fuzzy trapezoidal subset

228

El-Zakhema I., Aït Younesa A., Truck I., Greigec H. and Akdagd H. (2007).

COLOR IMAGE PROFILE COMPARISON AND COMPUTING.

In Proceedings of the Second International Conference on Software and Data Technologies - Volume ISDM/WsEHST/DC, pages 228-231

DOI: 10.5220/0001341802280231

 SciTePress

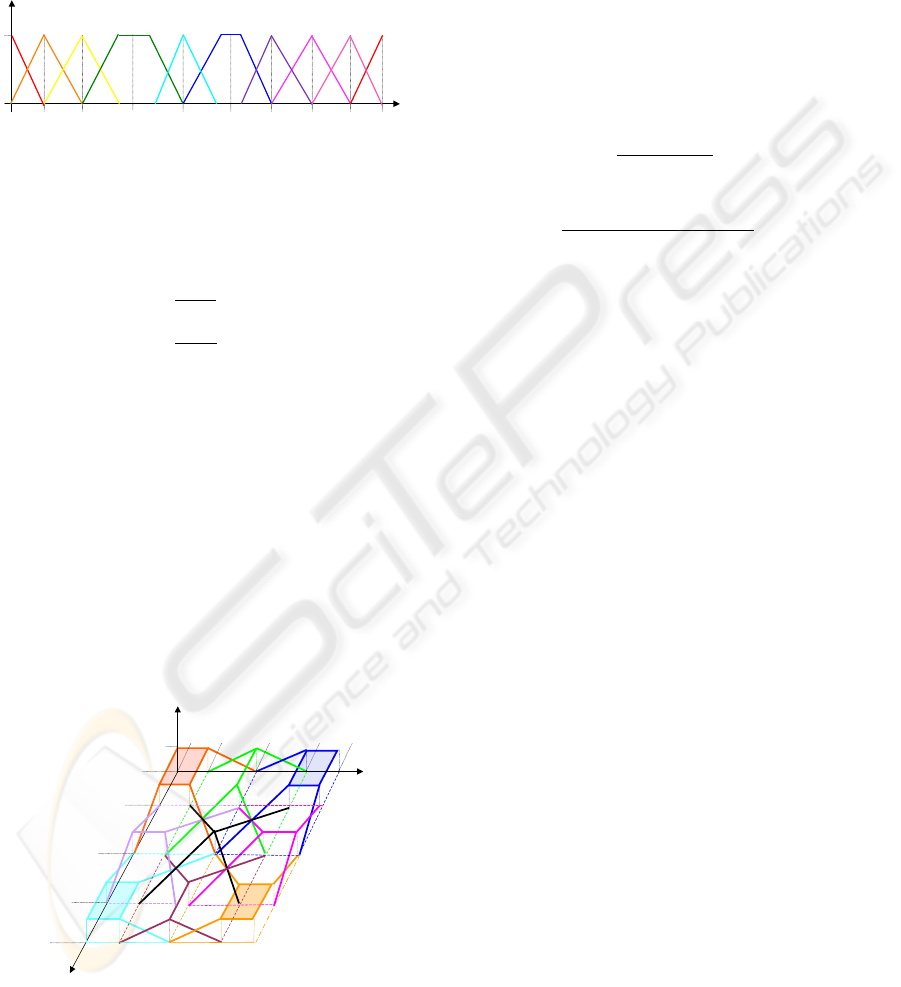
usually denoted by (a, b, c, d) with [a, d] the support

and [b, c] the kernel. When the kernel is reduced to

one point, it is a triangular subset denoted by (a, b, d).

Each subset shall intersect with its adjacent subsets to

avoid the colorless zones. For each color t of

T there

is a membership function f



H



128



170



191

213

234



255

0

1

red



orange



yellow



green



cyan



blue



purple



magenta



pink



red



Figure 1: The dimension H.

According to the values of Figure 1 we can get the

function f

for all colors.

∀t ∈ T , f

(h) =











1 if h ≥ b∧ h ≤ c

0 if h ≤ a∧ h ≥ d

h− a

b− a

if h > a∧ h < b

d − h

d − c

if h > c∧ h < d

2.2 Qualiﬁers and Achromatic Colors

The qualiﬁers are deﬁned by the saturation and light-

ness dimensions. Each colorimetric qualiﬁer is as-

sociated to one or both dimension(s). To facilitate

the process, each dimension interval is divided into

three equal sub-intervals: low, average and strong

value. As a result, we obtain nine “two dimension-

dependent” qualiﬁers denoted by Q = { somber, dark,

deep, gray, medium, bright, pale, light, luminous }.

Each qualiﬁer of Q is associated to a membership

function

with q ∈ Q. Thus, every function is repre-

sented through the 3 dimension-set (cf. Figure 2).



255

212

127430

0

43

127

212

255

S



1

Figure 2: Dimensions L and S.

Black, gray and white are achromatic “colors” that

are completely deﬁned through the spaces L and S

because they do not contain any hue (h is undeﬁned).

Inside the gray color we deﬁne three qualiﬁers: dark,

medium and light that are associated to fuzzy mem-

bership functions:

dark

medium

and

light

The membership degree of an image to a certain

class is deﬁned as follows:

Let I be an image and

P be the set representing

the pixels of I. Each element p of the set

P is deﬁned

by its color coordinates (h

, l

, s

). We can calculate

the functions f

, s

) for t ∈ T and q ∈ Q .

Let F

and

t,q

be the following functions, repre-

senting the membership degree of I to the classes t

and (t, q):

∀t ∈

T , F

(I) =

∑

p∈P

)

|P |

∀(t, q) ∈

T × Q ,

t,q

(I) =

∑

p∈P

, s

) × g

)

|P |

with g

) =



1 if f

) 6= 0

0 otherwise

The use of g

) is to assure that a qualiﬁer is not

assigned unless the relative hue is positive. Indeed an

image can not be “red bright” if it is not “red”.

3 COMPARABILITY

Two fuzzy subsets are called comparable if they are

close enough to each other. The degree of compa-

rability between 2 subsets will range from 0 (too far

or independent) to 1 (equality). Using the notion of

comparability with colors we are interested in know-

ing whether a certain color is said comparable to its

adjacent colors or not. The degree of comparability

of the subset B denoted by (a

, b

, c

, d

) to the sub-

set A denoted by (a

, b

, c

, d

)is:

γ(A, B) = avg( f

), f

)) (1)

The set of all subsets which are comparable (i.e γ is

strictly positive) to A is denoted Γ(A).

Considering a new color t

new

and an initial color t

state: t

∈ Γ(t

new

) iff γ(t

new

) > 0.

4 COMPATIBILITY

A certain image is characterized by blue if one of its

dominant colors is blue, in other words, the image

is blue if its membership degree in the blue color is

high enough. But the same image perhaps wouldn’t

be characterized by blue according to another user, or,

if the settings of blue color (variables a, b, c, d) have

been changed. Let us suppose that originally an im-

age I has a membership degree deg to color col, deg

COLOR IMAGE PROFILE COMPARISON AND COMPUTING

229

shall vary as soon as the settings of col changes. To

obtain the new degree deg

new

, the only way that gives

the exact result is to reprocess I, pixel by pixel. Our

approach avoids this long process by simulating the

variations of the colors’ initial settings by means of

some arithmetic calculations. The problem is similar

to a coordinate system transformation. So, for each

image, we recalculate its colorimetric proﬁle into a

new n-dimensional system. The new system is de-

ﬁned according to each user color perception.

For each col we select the subsets (i.e. the other

colors) whose degree of comparability with col is

high enough. Therefore we deﬁne a compatibility de-

gree only if the subsets are comparable. Indeed when

dealing with HLS space a small deviation can be ac-

ceptable (Boust et al., 2003) (Couwenbergh, 2003).

We should always keep in mind that colors are adja-

cent and that there shouldn’t be any hole in the fuzzy

partition of H.

We denote the comparability degree Φ as follows:

Φ(B, A) =

∩

(2)

where

is the surface of the initial subset A and

the surface of new subset B being compared to

It is obvious that Φ(B, A) 6= Φ(A, B), see Figure 3.

Figure 3: Notion of comparability.

4.1 Hue Compatibility

Let t

be an initial color represented by a fuzzy mem-

bership function f and by a

, b

, c

, d

, and let t

new

the new color represented by f

new

and a

, b

, c

, d

The new proﬁle of the image will be recalculated and

the adjacent colors of t

will also vary.

Figure 4: New deﬁnition for blue.

For example in Figure 4, the new blue is between

the initial blue and the initial green. Thus the mem-

bership of the image to the new color blue will be:

new

(I) = Φ(B

new

, B

)×F

(I)+Φ(B

new

, G

)×F

(I)

(3)

where B

is the standard function of Blue, G

is the

standard function of Green and B

new

is the new func-

tion of Blue.

The general function is deﬁned as follows:

new

(I) =

∑

∈Γ(t

new

)

Φ(t

new

) × F

(I) (4)

Assuming that the qualiﬁers depending on dimen-

sions L and S remain the same, we still have the same

values for the 9 qualiﬁers and only the functions on H

are modiﬁed, so we state:

∀(t

, q

) ∈

T × Q

new

∑

∀(t

)∈Γ(t

new

)

Φ(t

new

) ×

(I) (5)

4.2 Qualiﬁer Comparability

The same reasoning described above with H is in-

tended to be done with the other two dimensions S

and L. Each hue is being described by the qualiﬁers

so for each hue t

new

we calculate

new

Assuming that the qualiﬁers depending on S will

be modiﬁed, then, we have to calculate the new hue

qualiﬁed according to S thanks to the old hue qualiﬁed

according to S, so the equation is :

new

∑

∀(q

)∈Γ

)

Φ(q

, q

) ×

new

(I) (6)

where q

is the modiﬁed qualiﬁer on S.

In the same manner, we calculate the new hue and the

new saturation together contingent of the new light-

ness:

new

∑

∀(q

)∈Γ

)

Φ(q

, q

) ×

new

(I)

(7)

where q

is the modiﬁed qualiﬁer on L, Γ

the com-

patibility for L and Γ

compatibility for S.

We can demonstrate that the order of calculation of

the new saturation and the calculation of the new

lightness has no effect. The same results are reached

by any order of calculation.

5 THE APPLICATION

An application written in Java and PHP has been de-

veloped to test the method of comparability and com-

patibility. The blue and green colors are represented

ICSOFT 2007 - International Conference on Software and Data Technologies

230

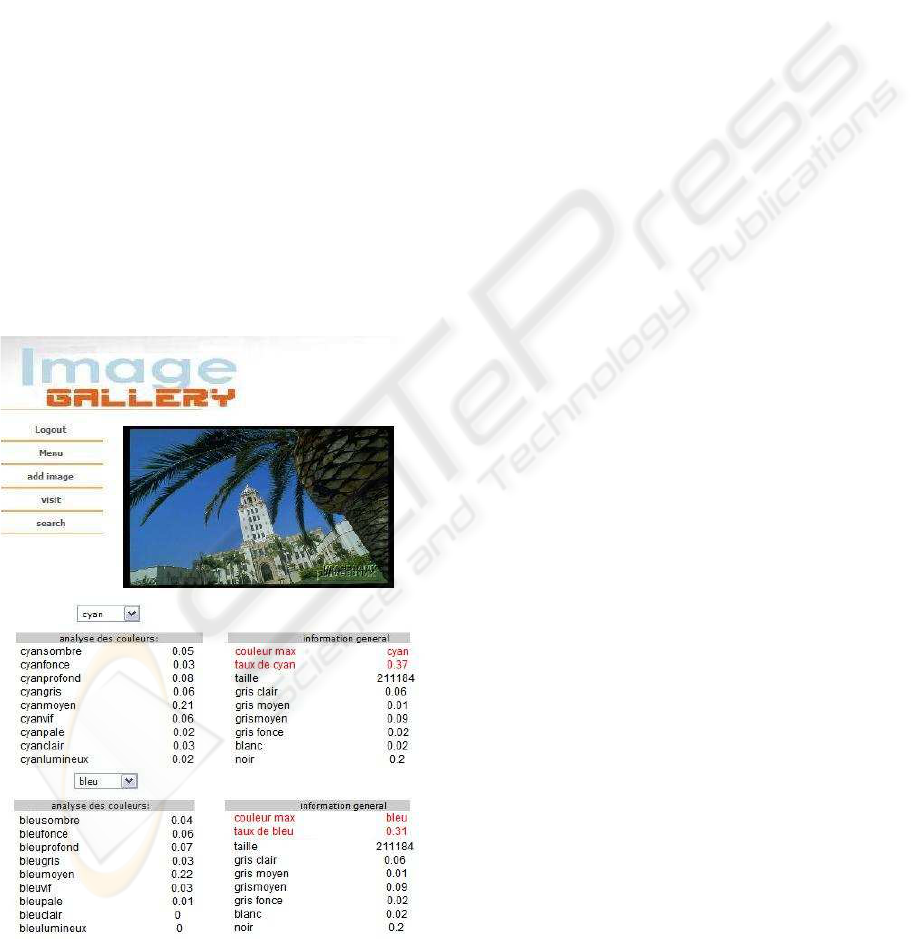
by trapezoidal fuzzy subset; all other colors are repre-

sented by triangular fuzzy subsets.

Each image inserted in the database is processed ac-

cording to the standard setting of colors; each pixel

is accessed and the RGB values are converted into the

HLS color space. By applying the functions f

and

the coordinates of each pixel in HLS are transformed

into membership degree in colors and qualiﬁers. So

a pixel may be considered 0.7 red and 0.3 orange. At

the end, the colorimetric proﬁle of the image is con-

structed. We store all values of the proﬁle in the table

prof. In the application, we can see for each image in

the menu visit the detailed colorimetric parameters.

In the menu search we can retrieve images by supply-

ing an argument such as blue, red pale etc. To test our

method of comparability and compatibility we insert

in the table HLS a new row. For example we keep

all values except for the colors cyan and blue: cyan

is shifted to the right while blue is shrunk. We ap-

ply the rules of comparability and compatibility on a

image/row in table photo. Now any image containing

some blue has a new colorimetric proﬁle: the values

for cyan increase. Figure 5 shows the results.

Figure 5: When modifying blue and cyan settings.

6 CONCLUSION

In this paper a new method is proposed to calculate

the membership degree of colors in an image. Ini-

tially we start building a colorimetric proﬁle of the

image based on an initial set of colors and qualiﬁers.

Since this initial set may vary according to the user’s

perception, we developed an algorithm that shall com-

pute the new colorimetric proﬁle. The computation of

the new proﬁle is based on the proﬁle constructed in

the initial phase and not on the image itself. Future

work, which has been already started, is to model the

user’s perception. The fuzziness of perception makes

its modeling a challenge and gives motivation to use

the fuzzy logic terms to do mapping between abstract

and concrete objects. We will focus on the dynamic

construction of the users’ proﬁles, which will increase

their satisfaction by being more personalized and ac-

commodated to their particular needs. Our work will

not affect only the image retrieving domain, but all

themes that rely on subjectivity and perceptions.

REFERENCES

ıt Younes, A., Truck, I., and Akdag, H. (2007). Image

retrieval using fuzzy representation of colors. In Soft

Computing - A Fusion of Foundations, Methodologies

and Applications, 11 (3), pp 287-298. Springer.

Boust, C., Chahine, H., Vi

enot, F., Brettel, H., Chouikha,

M. B., and Alqui

e, G. (2003). Color correction judge-

ments of digital images by experts and naive ob-

servers. In Proceedings of PICS 2003, pp. 4-9. PICS

2003.

Chen, Y. and Wang, J. Z. (2002). A region-based fuzzy

feature matching approach to content-based image re-

trieval. In IEEE Transactions on Pattern Analysis and

Machine Intelligence 24(9), pp. 1252-1267.

CIE (1987). Cie international lighting vocabulary. In CIE

International Lighting Vocabulary. CIE Publ.

Couwenbergh, J. P. (2003). Guide complet et pratique de la

couleur. Eyrolles, Paris, 2nd edition.

Herrera, F. and Mart

ınez, L. (2001). A model based on lin-

gustic two-tuples for dealing with multigranularity hi-

erarchical linguistic contexts in multiexpert decision-

making. In Transactions on Systems, Man and Cyber-

netics, Part B, 31(2), pp.227-234. IEEE.

Omhover, J. F., Detyniecki, M., and Bouchon-Meunier, B.

(2004). A region-similarity-based image retrieval sys-

tem. In Proceedings of IPMU’04.

Truck, I. and Akdag, H. (2003). Supervised learning us-

ing modiﬁers: Application in colorimetrics. In Pro-

ceedings of the ACS/IEEE International Conference

on Computer Systems and Applications.

COLOR IMAGE PROFILE COMPARISON AND COMPUTING

231