
A FORMAL APPROACH FOR THE DEVELOPMENT OF
AUTOMATED SYSTEMS
Olfa Mosbahi, Leila Jemni
LORIA, INRIA Lorraine, Nancy University, France
Facult
´
e des Sciences, El Manar II University, Tunisie
Jacques Jaray
LORIA, INRIA Lorraine, Nancy University, France
Keywords:
Automated systems, Event B method, Refinement, Language TLA
+
, Liveness properties, Verification.
Abstract:
This paper deals with the use of two verification approaches : theorem proving and model checking. We focus
on the event B method by using its associated theorem proving tool (Click
n Prove), and on the language
TLA
+
by using its model checker TLC. By considering the limitation of the event B method to invariance
properties, we propose to apply the language TLA
+
to verify liveness properties on a software behavior.
We extend first of all the expressivity of a B model (called temporal B model) to deal with the specification
of fairness and eventuality properties. Second, we give transformation rules from a temporal B model into
a TLA
+
module. We present in particular, our prototype system called B2TLA
+
, that we have developed to
support this transformation. Finally, we verify these properties thanks to the TLC model checker.
1 INTRODUCTION
In the paper, we propose to combine and apply two
techniques: theorem proving, when possible, and
model checking otherwise, in the construction and
verification of safe automated systems. The theorem
prover concerned is part of the B toolkit associated to
the event B method and the model checker is TLC for
TLA
+
models. The B event method provides us with
techniques and tools for specifying, refining, verify-
ing invariant properties and implementing systems. B
is not well suited to deal with liveness properties in
automated systems. The language, TLA
+
, provides
us with an abstract and powerful framework for mod-
elling, specifying and verifying safety, eventuality,
fairness behavioral properties of reactive systems.
We propose to define briefly the syntax and the se-
mantics of the extension of a B model (called tempo-
ral B) to deal with the specification of fairness and
eventuality properties. Then, we give the transfor-
mation rules from a temporal B model into a TLA
+
module and we present a prototype system called
B2TLA
+
supporting these transformation rules. Fi-
nally, we verify these properties thanks to the TLC
model checker. The second part of our contribution
describes a development method combining the two
methods with their associated tools.
We suppose that the specifier is familiar with the
use of the B technology but not with TLA
+
. He
uses the prototype system to translate a temporal B
model into a TLA
+
module and then he verifies live-
ness properties with the TLC model checker. To our
knowledge, there is no previous work which resolved
the problem that we tackle in this paper.
The paper is organized as follows : section 2
presents an overview of the event B method, section
3 presents an overview of the language TLA
+
, section
4 gives a description of the proposed approach using
a case study and section 5 ends with a conclusion and
perspectives.
2 OVERVIEW OF THE EVENT B
METHOD
The event B method (Abrial, 2003) is based on the B
notation (Abrial, 1996). It extends the methodolog-
ical scope of basic concepts such as set-theoretical
notations and generalized substitutions in order to
take into account the idea of formal models. Roughly
speaking, a formal model is characterized by a
(finite) list x of state variables possibly modified
by a (finite) list of events; an invariant I (x) states
304
Mosbahi O., Jemni L. and Jaray J. (2007).
A FORMAL APPROACH FOR THE DEVELOPMENT OF AUTOMATED SYSTEMS.
In Proceedings of the Second International Conference on Software and Data Technologies - SE, pages 304-310
DOI: 10.5220/0001342503040310
Copyright
c
SciTePress
some properties that must always be satisfied by the
variables x and maintained by the activation of the
events. Generalized substitutions provide a way to
express the transformations of the values of the state
variables of a formal model. An event consists of two
parts : a guard (denoted grd) and an action. A guard
is a predicate built from the state variables, and an
action is a generalized substitution (denoted GS).
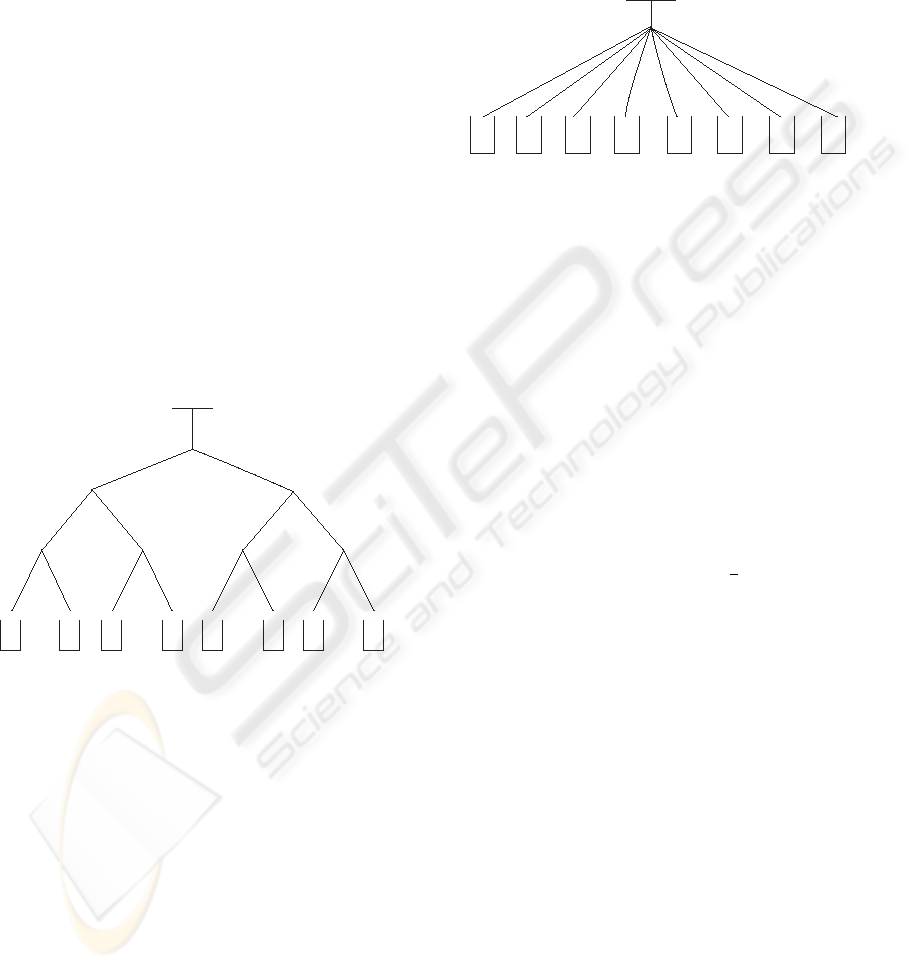
Example : A parcel sorting device.
In this section, we present an example of reactive sys-
tem : a parcel sorting device (Jaray and A.Mahjoub,
1996) which will be taken to illustrate our proposed
approach. We just give the abstract model of the sys-
tem and not the refinement steps. The problem is to
sort parcels into baskets according to an address writ-
ten on the parcel. In order to achieve such a sort-
ing function we are provided with a device made of
a feeder connected to the root of a binary tree made
of switches and pipes as shown in the figure 1. The
switches are the nodes of the tree, pipes are the edges
and baskets are the leaves. A parcel, thanks to gravity,
can slide down through switches and pipes to reach a
basket.
Feeder
0
1
2
3
4 5 6
7 8 9 10 11 12 13
14
1 2 3 4 5 6 7 8
Baskets
Figure 1: Router.
A switch is connected to an entry pipe and two
exit pipes, a parcel crossing the switch is directed to
an exit pipe depending on the switch position. The
feeder releases one parcel at a time in the router, the
feeder contains a device to read the address of the par-
cel to be released. When released, a parcel enters
a first switch (the root of the binary tree) and slides
down the router to reach a basket. The controller can
activate the feeder and change the switches position.
For safety reasons, it is required that switch change
should not occur when a parcel is crossing it. In order
to check this condition, sensors are placed at the entry
and the exits of each switch.
We consider a simplified version of the system
with only safety properties to illustrate a specification
with the event B method and we will deal in the fol-
lowing with liveness properties (eventuality and fair-
ness) to explain our approach.
Abstract model of the system
The abstract model of the system is given figure 2.
1 2 3 4 5 6 7 8
Baskets
channel
Feeder
Figure 2: Router.
The sorting device. The sorting device consists of a
feeder and a sorting layout. The feeder has two func-
tions: selection of the next parcel to be introduced into
the sorting layout and gate opening (releasing a par-
cel in the sorting layout). We introduce the events se-
lect and release to capture the two functions. In order
to produce the abstract model of the sorting layout,
we have to notice that a given state of the switches
forms a channel linking the entrance to a unique sort-
ing basket. A basket is an element of a set named
Baskets. Channels and sorting baskets are in a one to
one correspondence. Therefore, the abstract model of
the sorting device can be reduced to a single variable
channel taking the value of the sorting basket it leads
to, namely a value in the set Baskets. The channel
value is changed by the event set
channel.
Parcels. Parcels, as part of the environment, are rep-
resented as elements of a set we name PARCELS. We
use a total function (adr) from PARCELS to the inter-
val Baskets to refer to the parcels address. We give
the status ”arrived” to the parcel which has reached
a sorting basket. The variable (arrived) is a function
from PARCELS to Baskets. The goal of the sorting
system is to decrease the set of the parcels to sort. The
variable sorted represents the set of sorted parcels.
The remaining parcels are defined by the expression
PARCELS - sorted named UNSORTED. As pe is un-
defined when the sorting device is empty, we have in-
troduced a set PPARCELS of which PARCELS is a
proper subset; pe is an element of PPARCELS and
assignment of any value in PPARCELS - PARCELS
stands for ”undefined”. The expression PPARCELS -
PARCELS will be referred as NOPARCELS. The se-
lection of a parcel is an event which may be activated
once the device is free and the variable pe is unde-
fined, which means that no parcel is processed.
Moving parcels. In our abstraction a parcel takes no
time to travel from the feeder to a basket. A parcel
A FORMAL APPROACH FOR THE DEVELOPMENT OF AUTOMATED SYSTEMS
305

arrives in the basket to which the channel leads up.
When the event cross
parcel occurs, the current par-
cel sorting is finished and then, of course, the current
parcel becomes undefined.
The Controller. The controller has to ensure right
parcel routing. Two events are added for the con-
troller : Set
channel and Release. The event
Set
channel assigns to channel the value of adr(pe).
The event Release changes the state of the sorting de-
vice from free to busy. The model of the automated
system is presented in Figure 3.
Verification of the B model . All generated proof
obligations are verified with the B click
n Prove tool.
Requirement of liveness properties. In our example,
we need to consider the dynamics of the system. Our
model must take into account the following properties
:
1. Every parcel introduced in the entry eventually
reaches one of the baskets, this property is
described with :
∀p.(p ∈ UNSORTED ⇒
♦arrived (p) ∈ Baskets)
2. Every parcel introduced in the entry must reach
the basket corresponding to its destination ad-
dress, this property is described with :
∀p.(p ∈ UNSORTED) ; arrived (p) =
adr(p))
3. Weak fairness conditions on the events is as-
sumed.
These properties can not be specified in the clause
INVARIANT. We need to extend the expressivity of
event B to take into account such properties.
3 OVERVIEW OF THE
LANGUAGE TLA
+
TLA
+
is a language intended for the high level speci-
fication of reactive, distributed, and in particular asyn-
chronous systems. It combines the linear-time tempo-
ral logic of actions TLA (Lamport, 1994), and mathe-
matical set theory. The semantics of TLA is based on
behaviors of state variables.
A TLA specification of a system denoted by
Spec(S ) looks like : Init ∧ 2[Next]
x
∧ L where
Init is the predicate which specifies initial states
(s
0
[|Init|]), Next is an action (a relation) that de-
scribes the next-state relation and L is a fairness as-
sumption (strong or weak) on actions.
TLA
+
(Lamport, 2002) is an extension of TLA
with ZF set theory and modules for structuring a spec-
ification. A module is a text containing a name, a list
MODEL Parcel Sorting
SETS PPARCELS ; SortingState = {free , busy }
CONSTANTS PARCELS, adr, Baskets
PROPERTIES
PARCELS ⊂ PPARCELS ∧ PARCELS 6= ∅ ∧
Baskets 6= ∅ ∧ adr ∈ PARCELS → Baskets
VARIABLES
arrived, channel, sorting, pe, sorted, ready
to sort
INVARIANT
arrived ∈ PARCELS 7→ Baskets ∧ channel ∈ Baskets ∧
pe ∈ PPARCELS ∧ sorting ∈ SortingState ∧
ready
to sort ∈ BOOL ∧ sorted ⊆ PARCELS ∧
(sorting = busy ⇒ channel = adr(pe)) ∧
(sorting = busy ⇒ ¬ ready
to sort) ∧
(ready
to sort ⇒ channel = adr(pe)) ∧
(ready
to sort ⇒ pe ∈ PARCELS) ∧
∀p.(p ∈ PARCELS ∧ p ∈ dom(arrived) ⇒
arrived (p) = adr(p))
DEFINITIONS
UNSORTED == PARCELS - sorted ;
NOPARCELS == PPARCELS - PARCELS
INITIALISATION
arrived := {} || channel : ∈ Baskets || sorting := free ||
pe : ∈ NOPARCELS || sorted := {} ||
ready to sort := FALSE
EVENTS
select
parcel = ANY p Where p ∈ UNSORTED ∧
pe ∈ NOPARCELS ∧ sorting = free
THEN pe := p
END;
set
channel = SELECT sorting = free ∧ pe ∈ PARCELS
∧ ¬ ready
to sort
THEN channel := adr(pe) ||
ready
to sort := TRUE
END;
release = SELECT sorting = free ∧ pe ∈ PARCELS
∧
ready
to sort
THEN sorting := busy ||
ready
to sort := FALSE
END;
cross
parcel = SELECT sorting = busy
THEN arrived(pe) := channel ||
sorted := sorted ∪ { pe} ||
pe : ∈ NOPARCELS || sorting := free
END
END
Figure 3: Abstract model of the sorting device.
of definitions (constants, variables, operators, func-
tions, predicates, assumptions, theorems, proofs).
4 PROPOSED APPROACH
The event B method deals with safety properties,
but there are applications, such as automated or dis-
ICSOFT 2007 - International Conference on Software and Data Technologies
306
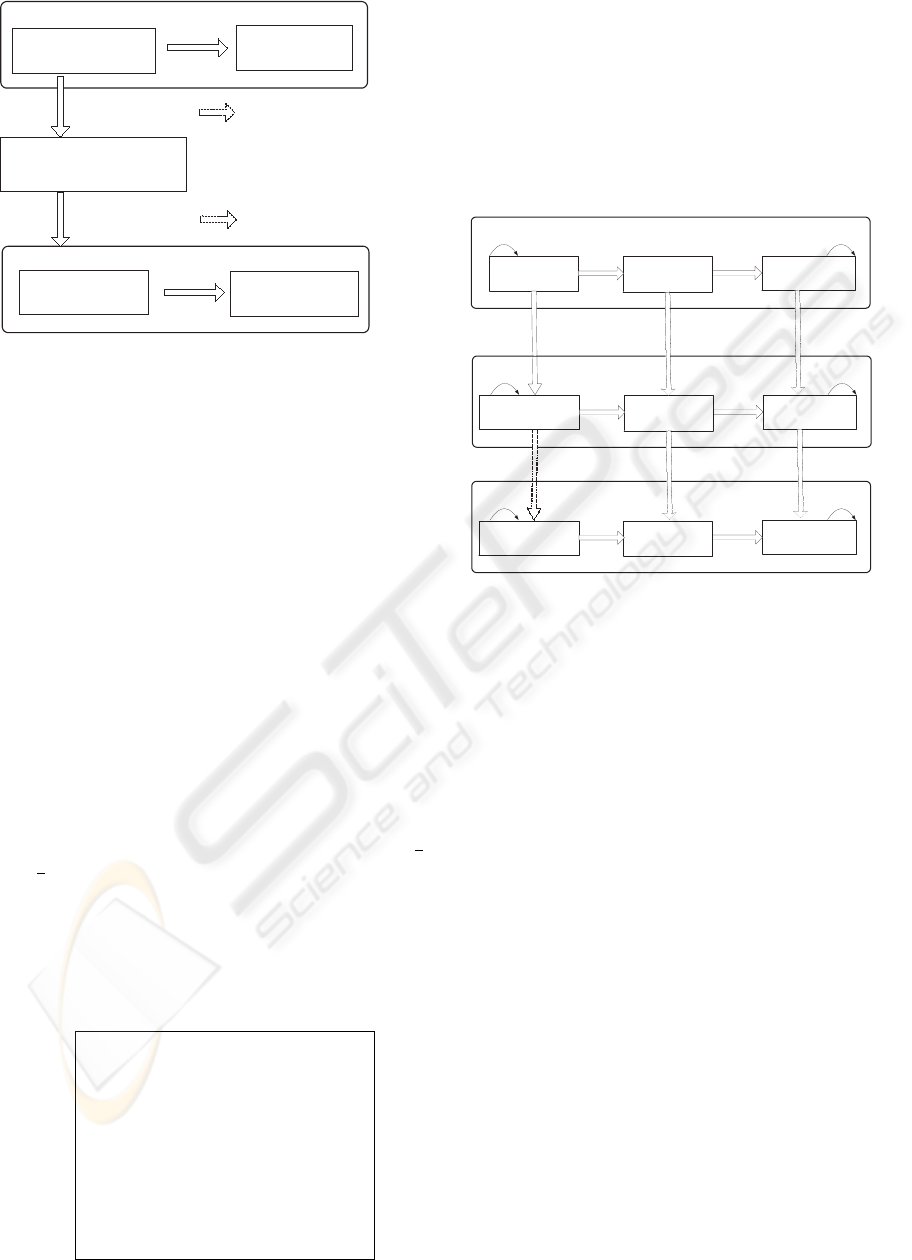
B Model of the automated system
Proof of the
Safety properties with B
toolkit
TLA+ module of the
automated system
Proof of liveness properties
with TLC
Translation into a TLA+module
Temporal B model of the automated system
Addition of liveness properties
Extending B notation
Extending semantics over traces
Using B2TLA+prototype
(1)
(2)
Figure 4: Translation of a B model into a TLA
+
module.
tributed systems, where liveness properties must be
considered. TLA
+
deals with safety, eventuality and
fairness properties. We suggest the use of TLA
+
be-
cause these two methods are very close with respect
to their foundations. In this proposed method, we
suppose that the specifier uses the event B method
for developing automated systems and he is not fa-
miliar with TLA
+
modelling. He uses the prototype
system B2TLA
+
, witch we have developed to trans-
form a temporal B model into TLA
+
module. Then he
can verifies liveness properties using the TLC model
checker.
The proposed approach as shown in figure 4 uses
the event B method and the temporal logic TLA
+
as
follows:
1. At first, an abstract model of the system is given in
the event B method where only invariance proper-
ties are considered,
2. Invariants properties are verified with the Click
n Prove tool,
3. Liveness properties are added to the abstract B
model when necessary. The FAIRNESS clause
is used for specifying fairness properties and
EVENTUALITY clause for the specification of
eventuality properties. The obtained model is as
follows :
MODEL hnamei
SETS hlist of setsi
CONSTANTS hconstantsi
PROPERTIES hPropertiesi
VARIABLES hvariablesi
INVARIANT hinvariantsi
INITIALISATION hinitialization of variablesi
EVENTS heventsi
FAIRNESS hFairness propertiesi
EVENTUALITY hEventuality propertiesi
END
4. The new temporal model is then translated into
a TLA
+
module using the prototype system
B2TLA+ which we have developed,
5. Liveness properties are checked with TLC,
6. In each refinement step, we repeat the steps 1, 2, 3
and 4 until satisfying all properties of the system.
The refinement is shown in the figure 5.
Abstract B model of the
automated system
Abstract TLA+module of the
automated system
Transformation to a
TLA+module
Refinement 1
Proof of safety properties
with B toolkit
Adjunction of
liveness properties
Proof of liveness
properties with TLC
First refinement of the
automated system
Temporal abstract B model
of the automated system
TLA+ refinement of
Transformation to a
TLA+module
Adjunction of
liveness properties
Temporal first refinement of
the automated system
with B toolkit
Refinement n of the
automated system
TLA+ refinement of the
automated system
Transformation to a
TLA+module
Adjunction of
liveness properties
Temporal refinement n of the
automated system
Refinement n
Proof of liveness
properties with TLC
Proof of liveness
properties with TLC
Refinement 1
Refinement 1
Refinement n Refinement n
Proof of safety properties
with B toolkit
Proof of safety properties
with B toolkit
Proof of refinement
with TLC
Proof of refinement
with B toolkit
Proof of refinement
with TLC
Proof of refinement
with B toolkit
the automated system
Figure 5: Refinement for automated systems development.
In the sequel we will focus on the translation of
the extended B model into a TLA
+
module and the
presentation of the prototype B2TLA
+
.
Translation rules from a B model into TLA
+
mod-
ule.
In this section, we present translation rules from a
temporal B model into a TLA
+
module. The tables
below show the correspondance between B syntax
and TLA
+
one.
- Clauses key word correspondance. In the table be-
low, we will give the different clauses from a tem-
poral B model translated in a TLA
+
module.
- Modelling of data. Both B and TLA
+
are based
on Zermelo-Frankel set theory in which every
value is a set. The modelling of data is based on
constants, variables, sets, relations and functions.
In the tables below, we will give the translation
rules of data from a temporal B model to a TLA
+
module.
The event B method has used a simplification of
classical set theory. The only basic set classical
theoretic constructs axiomatized are the most nat-
ural ones : cartesian product (×), power-set (P)
A FORMAL APPROACH FOR THE DEVELOPMENT OF AUTOMATED SYSTEMS
307
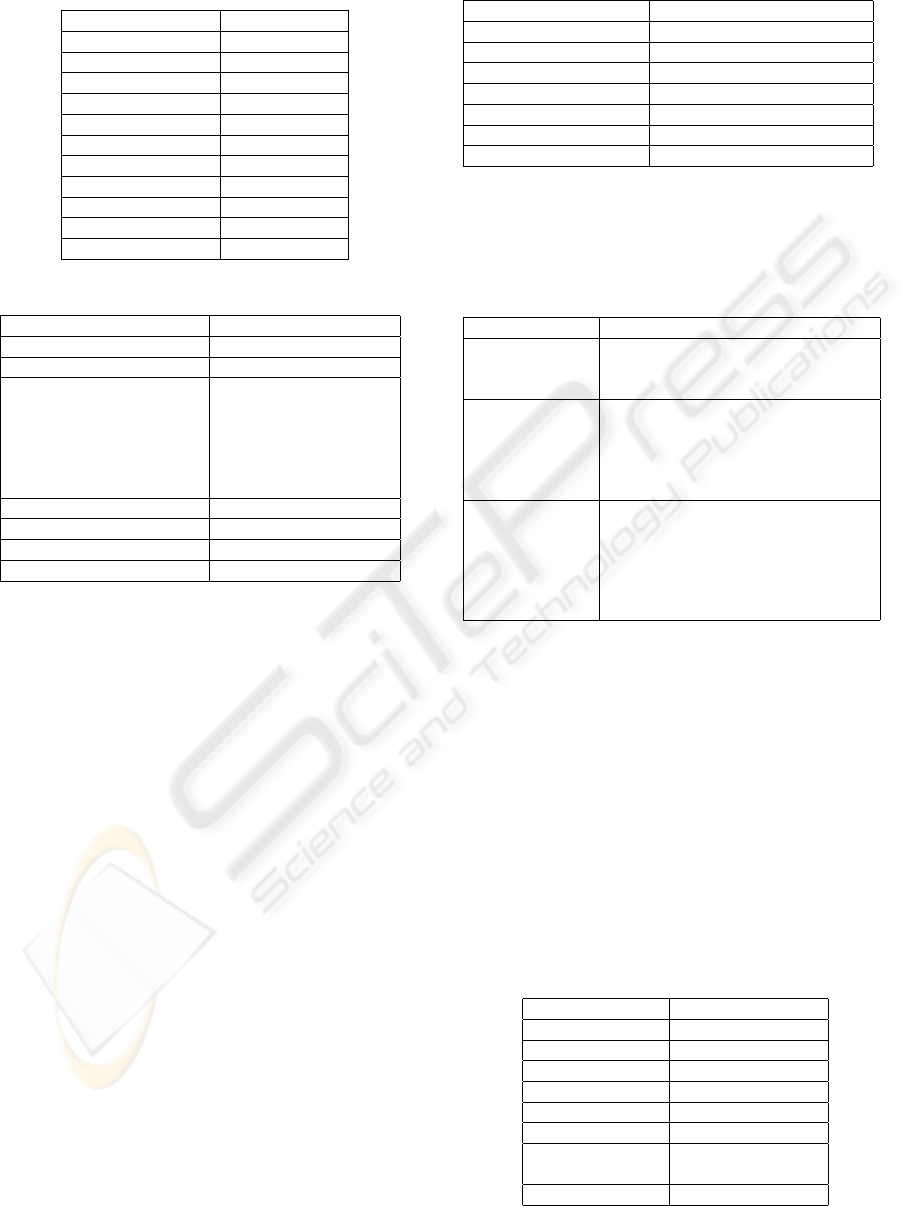
Table 1: Correspondance with clauses.
B model TLA+ module
SYSTEM MODULE
REFINEMENT MODULE
REFINES EXTENDS
CONSTANTS CONSTANTS
VARIABLES VARIABLES
PROPERTIES ASSUME
INVARIANT INVARIANT
INITIALISATION INIT
ASSERTIONS THEOREM
FAIRNESS FAIRNESS
EVENTUALITY LIVENESS
Table 2: Constants, Variables and Sets.
B model TLA+ module
c
1
,c
2
in CONSTANTS c
1
,c
2
in CONSTANTS
v
1
,v
2
in VARIABLES v
1
,v
2
in VARIABLES
E
1
in SETS E
1
in CONSTANTS
E
2
= {x
1
,..,x
n
} in SETS x
1
,..,x
n
in
CONSTANTS and
E
2
= {x
1
,..,x
n
}
occurs after the clause
ASSUME
{e
1
,....,e
n
} {e
1
,....,e
n
}
{x |x ∈ S ∧ P} {x ∈ S : P }
{e|x ∈ S } {e : x ∈ S }
P(S ) SUBSET S
and set comprehension ({ | }). A set is defined in
comprehension with respect to another set s when
the members of the former are exactly the mem-
bers of s satisfying a certain predicate. The set
theory in TLA
+
is based on the simple forms of
the constructs {x ∈ S : P } (the subset of S con-
sisting of all elements x satisfying property P )
and {e : x ∈ S } (the set of elements of the form
e, for all x in the set S ) as primitives, and the
more general forms are defined in terms of them.
In TLA
+
, the two powerful operators of set the-
ory are UNION and SUBSET, defined as follows
: UNION S is the union of the elements of S and
SUBSET S is the set of all subsets of S . T ∈
SUBSET S iff T ⊆ S (it is the power set of P(S)
or 2
S
). We find correspondance between the B
and TLA
+
set theories.
In the table below, we will give correspondance
between functions in B and TLA
+
.
In the table 3, the symbols →, 7→ ։, S 7։ T ,
,S 7 T describes respectively total and partial
function, total and partial surjection and total and
partial injection. We associate the value undef to
the elements where the function is not defined be-
cause in TLA
+
we have just total function.
- Events. Events in B method are actions in the tem-
Table 3: Functions translation.
B model TLA+ module
f (e) f [e]
Dom(f ) Domain f
(λx .x ∈ S |e) [x ∈ S 7→ e]
S → T ,S ։ T ,S T [S → T ]
S 7→ T ,S 7։T ,S 7T [S → T ∪ undef ]
f [S ] Image(f , S ) ≡ {f [x ] : x ∈ S}
f (x ) := y f
′
= [f EXCEPT![x ] = y]
poral logic TLA
+
; in the following, we give the
translation of the three event types B into TLA
+
actions.
Table 4: Events translation.
B event TLA+ action
E ≡ BEGIN E ≡ ∧P(x ,x
′
)
x : P (x
0
,x ) ∧UNCHANGEDhvarsi
END;
E ≡ SELECT E ≡ ∧G(x )
G(x ) ∧Q(x ,x
′
)
THEN ∧UNCHANGEDhvarsi
x : Q(x
0
,x )
END;
E ≡ ANY E ≡ ∃t : ∧G(t,x )
t WHERE ∧R(x,x
′
,t)
G(t, x ) ∧UNCHANGEDhvarsi
THEN
x : R(x
0
,x ,t)
END;
- Safety properties. The syntax of safety properties
in B and TLA
+
are quite similar because the two
methods are based on the first order logic. The
table 5 provides a translation of safety formulae
from B to TLA
+
.
- Liveness properties. The translation is obvious be-
cause the extension is inspired by the syntax of
TLA
+
. In the following, we give the translation
rules of liveness properties from a B model to a
TLA
+
module.
Where e is an event in B and an action in TLA
+
,
Table 5: Translation of safety formulae from B to
TLA
+
.
B formula TLA
+
formula
P P
¬P ¬P
P ∧ Q P ∧ Q
P ∨ Q P ∨ Q
P ⇒ Q P ⇒ Q
P ⇔ Q P ⇔ Q
!x .(P ⇒ Q ) ∀x : (P ⇒ Q )
!(x ,y).(P ⇒ Q) ∀(x , y) : (P ⇒ Q)
∃x .(P ∧ Q) ∃x : (P ∧ Q)
ICSOFT 2007 - International Conference on Software and Data Technologies
308
Table 6: Translation of temporal formulae.
B formula TLA+ formula Definition
WF (e) WF (e) weak fairness
for the event e
SF (e) SF (e) strong fairness
for the event e
F ; G F ; G F leads to G
F F F is always true
♦F ♦F F is eventually true
F and G are liveness properties.
The prototype system B2TLA
+
.
The transformation of a B model into TLA
+
mod-
ule is based on the technique of translation syntax-
directed which consists in adding semantics actions
in the B grammar to obtain an equivalent TLA
+
mod-
ule. Based on our approach to ensure the verifica-
tion of safety and liveness properties, we implement
a prototype system. The figure 6 describes the archi-
tecture of the system. The prototype system is im-
plemented using the Flex-Yacc tool. Liveness prop-
erties are given by the user. He introduces fairness
conditions and eventuality properties to be verified.
He gives the fairness condition (weak fairness, strong
fairness) for each event. These properties are added
to a B model to obtain a temporal B model.
by syntax
Source B
model
Extension with
liveness properties
proved B
model
Proof of
invariance using
with B toolkit
Temporal B
model
Extended BNP grammar
with liveness properties
Translation
Lexical
analysis
syntaxic
analysis
Type
checker
TLA+ code
generation
TLA+ module
Liveness checking
with TLC
Verified module
TLA+
Fairness conditions
Eventuality properties
Figure 6: The proposed method using the prototype system
B2TLA+.
Application to the example.
In the following, we give the module TLA
+
obtained
after translation of a B temporal model.
The TLC model checker can check a finite model
of a specification obtained by instantiating the con-
stant parameters and, if necessary, specifying con-
straints to make the set of reachable states finite. With
TLC, we can check that a specification satisfies invari-
ance or liveness specifications. Also, we can check
refinement such that a TLA
+
specification implies an-
other using TLC.
MODULE Parcel Sorting
EXTENDS Naturals
CONSTANTS PPARCELS , PARCELS , Baskets,
noBaskets, adr , free, busy
VARIABLES channel , sorting, pe, sorted, arrived ,
ready
to sort
ASSUME adr ∈ [PARCELS → Baskets]
∧ PARCELS 6= {}
∧ Baskets 6= {}
∧ PARCELS ⊆ PPARCELS
∧ PARCELS 6= PPARCELS
∧ noBaskets /∈ Baskets
SortingState
∆
= {free, busy}
TypeInvariant
∆
=
∧ channel ∈ Baskets ∪ {noBaskets}
∧ sorting ∈ SortingState
∧ pe ∈ PPARCELS
∧ ready
to sort ∈ BOOLEAN
∧ arrived ∈ [PARCELS → Baskets]
∧ sorted ⊆ PARCELS
UNSORTED
∆
= PARCELS \ sorted
NOPARCELS
∆
= PPARCELS \PARCELS
Init
∆
= ∧ channel = noBaskets ∧ sorting = free
∧pe ∈ NOPARCELS
∧ arrived = [p ∈ PARCELS 7→ noBaskets]
∧sorted = {} ∧ ready
to sort = FALSE
select
parcel
∆
= ∧ sorting = free
∧ pe ∈ NOPARCELS
∧∃p ∈ UNSORTED : ∧ pe
′
= p
∧ UNCHANGED hchannel , arrived , sorted ,
sorting, ready
to sort i
set
channel
∆
= ∧ sorting = free
∧ pe /∈ NOPARCELS
∧ ready
to sort = FALSE
∧ channel
′
= adr [pe]
∧ ready
to sort
′
= TRUE
∧ UNCHANGED harrived, sorted, pe, sortingi
release
∆
= ∧ ready
to sort = TRUE
∧ sorting = free ∧ pe ∈ PARCELS
∧ sorting
′
= busy
∧ ready
to sort
′
= FALSE
∧ UNCHANGED hchannel , arrived , sorted , pei
cross
parcel
∆
= ∧ sorting = busy
∧ arrived
′
= [arrived EXCEPT ![pe] = channel ]
∧ sorted
′
= sorted ∪ {pe} ∧ pe
′
∈ NOPARCELS
∧ sorting
′
= free
∧ UNCHANGED hchannel , ready
to sort i
Next
∆
= ∨ select
parcel ∨ set channel
∨ release ∨ cross
parcel
trvars
∆
= hchannel , sorting, pe, arrived , sorted, ready to sort i
Fairness
∆
= WF
trvars
(select
parcel)
∧WF
trvars
(set
channel)
∧WF
trvars
(release)
∧WF
trvars
(cross
parcel)
Spec
∆
= Init ∧ 2[Next]
trvars
∧ Fairness
Invariant
∆
=
∧ sorting = busy =⇒ channel = adr [pe]
∧ sorting 6= free =⇒ pe ∈ PARCELS
∧ sorting = busy =⇒ ready
to sort = FALSE
∧ ready
to sort = TRUE =⇒ channel = adr [pe]
∧ ready
to sort = TRUE =⇒ pe ∈ PARCELS
Liveness
∆
=
∧ ∀p ∈ UNSORTED ; arrived [p] = adr [p]
∧ ∀ p ∈ UNSORTED =⇒ ♦arrived[p] ∈ Baskets
THEOREM Spec =⇒ 2TypeInvariant
THEOREM Spec =⇒ 2Invariant
THEOREM Spec =⇒ Liveness
5 CONCLUSION
In this paper we propose a method for the specifica-
tion and verification of safety and liveness properties
using the event B method and TLA
+
with their as-
sociated tools. We first extende the expressivity of
the event B method to deal with fairness and eventu-
ality properties. Second we propose a semantics of
A FORMAL APPROACH FOR THE DEVELOPMENT OF AUTOMATED SYSTEMS
309

the extension in terms of traces, in the same spirit as
TLA
+
does. Third we give transformation rules from
a temporal B model to a TLA
+
module and we de-
velop a prototype system (B2TLA
+
) which supports
this translation. Then we verify these properties us-
ing the TLC model checker. Our main idea is to start
with an abstract B model of the system under devel-
opment and then we verify all invariants of the model.
We use a proof tool which supports automatic and in-
teractive proof procedures. For the expression and
the verification of fairness and eventuality properties,
we can’t use the event B method because its seman-
tics is expressed in the weakest precondition calcu-
lus. Our goal is to give a temporal meaning to a B
model and then transform it to an equivalent TLA
+
module. TLA
+
and B are quite similar, both being
based on simple mathematics and when a system is
viewed as a set of events, it is easy to characterize it
by a TLA
+
specification. TLA
+
stands as a semantical
framework for an extension of B and the expression
of fairness and eventuality constraints is a very pow-
erful point of TLA
+
. Then, we verify these properties
thanks to the TLC model checker. TLC allows us to
analyse finite-state instances.
In future work, for the verification of infinite-state
systems, we propose the use of the predicate dia-
grams (Cansell et al., 2001). These diagrams are finite
graphs whose nodes are labelled with sets of predicate
and whose edges are labelled with action names. Be-
sides abstract states and state transition which are nec-
essary to reason about safety properties of systems,
predicate diagrams also include annotation related to
fairness conditions and well-founded orderings and
can therefore be used to reason about liveness proper-
ties. We plan to use these predicate diagrams to ver-
ify infinite-state-model and also refinement between
temporal B refinements. We plan to use also DIXIT,
a graphical toolkit supporting the use of predicate di-
agrams, which includes annotations for proving live-
ness properties. It is a graphical editor for drawing
predicate diagrams and proof obligations for proving
correctness of the specifications. The toolkit also sup-
ports stepwise development of systems, based on a
notion of refinement of predicate diagrams.
ACKNOWLEDGEMENTS
Thanks to Stephan Merz for serious comments on an
earlier draft of this paper.
REFERENCES
Abrial, J.-R. (1996). Extending B without changing it
(for developing distributed systems). In Habrias, H.,
editor, Proceedings of the 1st Conference on the B
method, pages 169–191.
Abrial, J.-R. (2003). B# : Toward a synthesis between Z and
B. In Bert, D., Bowen, J. P., King, S., and Wald
´
en, M.,
editors, ZB’2003 – Formal Specification and Devel-
opment in Z and B, volume 2651 of Lecture Notes in
Computer Science (Springer-Verlag), pages 168–177,
Turku, Finland. Springer.
Cansell, D., M
´
ery, D., and Merz, S. (2001). Diagram re-
finements for the design of reactive systems. Journal
of Universal Computer Science, 7(2):159–174.
Jaray, J. and A.Mahjoub (1996). Une mthode itrative de
construction d’un modle de systme ractif . TSI, 15. .
Lamport, L. (1994). The temporal logic of actions. ACM
Transactions on Programming Languages and Sys-
tems, 16(3):872–923.
Lamport, L. (2002). Specifying Systems, The TLA+ Lan-
guage and Tools for Hardware and Software Engi-
neers. Addison-Wesley.
ICSOFT 2007 - International Conference on Software and Data Technologies
310
