
HYPERSET/WEB-LIKE DATABASES AND THE EXPERIMENTAL
IMPLEMENTATION OF THE QUERY LANGUAGE DELTA
Current State of Affairs
Richard Molyneux and Vladimir Sazonov
Department of Computer Science, University of Liverpool, Ashton Street, Liverpool, United Kingdom
Keywords:
Web-like, semistructured, distributed databases, hypersets, bisimulation, query language Delta.
Abstract:
The hyperset approach to WEB-like or semistructured databases is outlined. WDB is presented either (i) as a
finite edge-labelled graph or, equivalently, (ii) as system of (hyper)set equations or (iii) in a special XML-WDB
format convenient both for distributed WDB and for including arbitrary XML elements in this framework. The
current state of affairs on experimental implementation of a query language ∆ (Delta) to such databases—the
main result of this paper—is described, with consideration of further implementation work to be done.
1 INTRODUCTION
It appears that the great success of Codd’s relational
approach to databases (Codd, 1983) was based on
taking the most fundamental concepts of logic and
set theory as its foundation. Thus, any relation is a
set of tuples, each tuple being also represented by a
set of a special kind. From the second half of the
1990s a new idea of semistructured databases (SSDB)
emerged; see (Abiteboul et al., 2000) as a general
reference. In the age of the Internet and the World-
Wide Web, allowing accessibility of remote and het-
erogeneous databases, the relational paradigm has be-
come too narrow and restrictive. The structure of the
data over the Internet is typically non-fixed or non-
uniform. The idea of graph representation of data
was introduced with interpretation of graph (directed)
edges like links to browse the Web. Furthermore, be-
cause of such “browsing”, considering the graph as a
binary (or ternary, if taking labels on edges into ac-
count) relation is not fully adequate in this context.
That is, intuitively this is something more than just
a relation. Indeed, interpreting end nodes of outgo-
ing edges from any given node n as “children” or
even as “elements” of n becomes more appropriate.
In particular, the latter is the terminology of XML—
the widely adopted approach to semistructured data
(however, tree-like rather than graph-like).
This also leads us again to a set theoretic idea of
representation of data—now semistructured data—a
far going generalization of the relational approach. It
is also worth noting that in the foundations of mathe-
matics, the previous century was marked by the tri-
umph of the set theoretic approach for representat-
ing mathematical data (the concepts) as well as the
style of mathematical language and reasoning. Math-
ematical logicians also developed generalized com-
putability theory over abstract sets (of sets of sets,
etc.) in the form of admissible set theory (Barwise,
1975). In computer science, a set theoretic program-
ming language SETL was created (quite naturally,
for the case of finite sets only). Also some the-
oretical considerations on computability and query
languages over hereditarily finite sets were done
in (Dahlhaus and Makowsky, 1986; Dahlhaus and
Makowsky, 1992; Sazonov, 1987; Sazonov, 1993)
with the perspective of a generalized set-theoretically
presented databases—in fact semistructured ones—
even before the term “semistructured databases” had
arisen. Moreover, the set theoretic approach is closely
related with a special version of the graph approach.
Probably the first mathematical result relating both
approaches was Mostowski’s Collapsing Lemma al-
lowing to interpret graph nodes as sets of sets corre-
sponding to children of these nodes. This, however,
worked properly only for well-founded graphs and
sets (which in the finite case, especially interesting
for database applications, means the absence of cy-
cles). But arbitrary graphs, even with cycles can also
be “collapsed” into sets (interrelated by the member-
ship relation) in the more general non-well-founded
set theory called also hyperset theory (Aczel, 1988;
Barwise and Moss, 1996). Here, for example the set
Ω = {Ω} consisting of itself and corresponding to the
29
Molyneux R. and Sazonov V. (2007).
HYPERSET/WEB-LIKE DATABASES AND THE EXPERIMENTAL IMPLEMENTATION OF THE QUERY LANGUAGE DELTA - Current State of Affairs.
In Proceedings of the Second International Conference on Software and Data Technologies - Volume ISDM/WsEHST/DC, pages 29-37
DOI: 10.5220/0001343200290037
Copyright
c
SciTePress
loop graph is quite a legal and meaningful thing.
These two trends (from set theory to semistruc-
tured databases as graphs and vice versa) were called
in (Sazonov, 2006) top-down and bottom-up ap-
proaches to semistructured databases. They meet
most closely in the work (Buneman et al., 2000)
which is devoted to a specific graph approach to
semistructured data considered up to bisimulation.
The latter concept is the key one in (Lisitsa and
Sazonov, 1997; Lisitsa and Sazonov, 1999) for inter-
preting graph nodes as a system of hypersets belong-
ing one to another according to the graph edges. Nev-
ertheless, (Buneman et al., 2000) is still rather a graph
approach than hyperset one according to the special,
however related to, but not a genuine set theoretical
way as graphs are treated there; cf. (Sazonov, 2006).
Note that the alternative and popular XML rep-
resentation of semistructured databases besides being
based mainly on the idea of a finite tree (not arbi-
trary graph), assumes a fixed order on the children
of any node, and therefore can not be considered as
a (hyper)set approach. Also, any graph representa-
tion like in (Abiteboul et al., 1997; McHugh et al.,
1997) which does not assume considering graphs up
to bisimulation (to thereby make the nodes into ab-
stract hypersets) is outside of the hyperset view.
The goal of this paper is to demonstrate how
theoretical ideas of hyperset approach to semistruc-
tured (which can be also naturally called Web-like)
databases (WDB) could be implemented and poten-
tially applied in the form of a practically working
query language Delta to such data. More precisely,
we want to demonstrate that this is working in prin-
ciple. The real practical work on efficiency as well
as many other questions which should be resolved for
any realistic database management system should be
inevitably postponed here because this is rather work
for a team of developers. However, we will present
here some related considerations.
Organizing the paper. Section 2 is devoted to the
background of the hyperset view to SSD/WDB with
the details of how it is represented in terms of sys-
tems of set equations. Also an appropriately restricted
XML (XML-WDB) format is introduced to repre-
sent set equations and to make this approach easily
adapted to already widely accepted XML. It is as-
sumed, in fact, a distributed version of a hyperset
based WDB somewhat similar to, but not necessarily
so huge as the WWW. Section 3 introduces the theo-
retical version of the language Delta and gives quick
outline of the implemented version of Delta by exam-
ples of queries. Section 4 describes how such queries
can be executed, again by examples. Section 5 out-
lines what should be done to make this language more
practically applicable and efficient. We conclude in
Section 6 by making some comparisons.
2 HYPERSET APPROACH TO
WDB
The set theoretic and, more generally, hyperset ap-
proach (Sazonov, 1993; Lisitsa and Sazonov, 1997;
Leontjev and Sazonov, 2001; Sazonov, 2001) to WDB
is based on the concept of hereditary finite sets or
more generally on hyperset theory (Aczel, 1988; Bar-
wise and Moss, 1996). Such semi-structured data is
represented as abstract sets of sets of sets, etc., even
with the possibility of cycles. For visualisation pur-
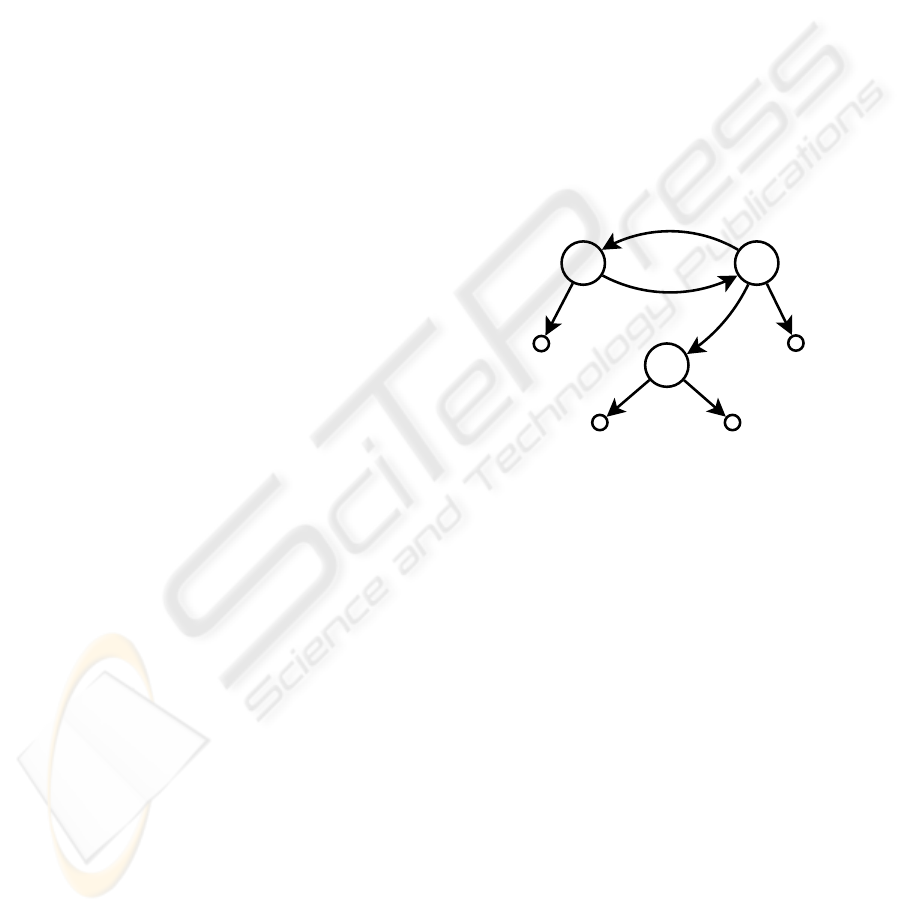
poses, hyperset databases are represented by graphs
(as depicted in Figure 1) with directed edges repre-
senting the membership relations.
name
"Alice"
"Sam" "cat"
species
name
name
"Bob"
pet
bob alice
husband
wife
sam
Figure 1: Example WDB representing a fictitious family.
However, when considering implementation (and also
intuitively) it is far more appropriate to represent
WDB by corresponding system of set equations. Each
set equation consists of a set name equated to the
corresponding bracket expression, were labelled el-
ements (of the set) may be either atomic values or
nested bracket expressions or set names described
in other equations. For example, the system of
“unnested” or “flat” set equations generated by the
graph in Figure 1 (and vice versa) looks as follows:
bob = {name:"Bob", wife:alice}
alice = {name:"Alice", husband:bob, pet:sam}
sam = {name:"Sam", species:"cat"}
or, equivalently, with the nesting allowed:
bob = {name:"Bob", wife:alice}
alice = {name:"Alice", husband:bob,
pet:{name:"Sam", species:"cat"} }
In particular, this demonstrates that the specific form
of set names
bob
,
alice
,
sam
however helpful intu-
itively is formally not important. They can always
be renamed (say, by numbered “object identities” like
&23
, etc.) or substituted as above. The proper infor-
mation on the WDB is carried by (i) labels on WDB-
graph edges (
name
,
wife
,
husband
, etc.), (ii) atomic
ICSOFT 2007 - International Conference on Software and Data Technologies
30

data on leaves (
"Bob"
,
"Alice"
), and (iii) the graph
structure or, respectively set-element nesting.
Note 1 Atomic data is in fact treated as labels
on additional leaf edges or, equivalently, as sin-
gleton sets consisting of a (labelled) empty set
(
"Bob" = {Bob:{}}
).
2.1 Bisimulation
In contrast to XML, the order and repetition of the
elements in set equations play no role. This leads
to the well-known (see e.g. (Aczel, 1988)) concept
of bisimulation relation between graph nodes or set
names (n
1
≈ n
2
). This relation (and corresponding re-
cursive algorithm) is based on the idea that any two
sets are equal (or two set names and corresponding
graph nodes are bisimilar) if for each (labelled) ele-
ment of the first set there exists an equal (bisimilar) el-
ement in the second set, and vice-versa. Bisimilar set
names are said to denote the same abstract (hyper)set.
Thus, we are considering WDB-graph (or system of
set equations) up to bisimulation which makes this
approach more than just a pure graph theoretic one.
WDB is called strongly extensional (Aczel, 1988) or
non-redundant if different nodes (set names) are non-
bisimilar i.e. denote different hypersets. This also
means that ≈ coincides with =.
2.2 WDB and XML
Although set equations represent WDB in the most
natural and intuitive way directly suggesting that
our data are hypersets, it makes sense to relate
this approach to the popular XML representation of
semistructured data and probably to use appropriate
existing techniques. Also numerous existing XML
data can be treated by our approach what can make
its application range considerably wider.
The main idea of the XML representation of any
system of set equations consists in (recursive) replac-
ing any labelled bracket expression
label : {...}
by XML element
<label>...</label>
. More pre-
cisely, the nested version of the system of set equa-
tions above (for Figure 1) is represented as an XML
document in the following special XML-WDB format:
<?xml version="1.0"?>
<set:eqns xmlns:set="...">
<set:eqn set:id="bob">
<name>Bob</name>
<wife set:ref="alice" />
</set:eqn>
<set:eqn set:id="alice">
<name>Alice</name>
<husband set:ref="bob" />
<pet>
<name>Sam</name>
<species>cat</species>
</pet>
</set:eqn>
</set:eqns>
Here
set:id
is the required attribute of
set:eqn
el-
ement and should have a unique (across the whole
document) value called also set name. Any other at-
tributes, except
set:ref
, are also allowed in the el-
ement
set:eqn
. The attribute
set:ref
must refer
to some existing
set:id
(possibly multiple—having
the attribute type
IDREFS
). The elements
set:eqn
are
allowed to contain arbitrary XML sub-elements with
arbitrary attributes (except
set:id
) and text data.
Such a XML-WDB document can be treated as a
system of set equations by using the following simple
transformations which can be done in arbitrary order:
•
<set:eqn set:id="setname">...</set:eqn>
is replaced by equation
setname = {...}
.
• any attribute (say, with two values)
attr =
"value1 value2"
, except the distinguished at-
tributes
set:id
and
set:ref
, is removed and re-
placed by sub-elements
<attr>value1</attr><attr>value2</attr>
.
Thus, attributes are treated as tags.
•
any text data
transforms to the sequence of
empty sub-elements
<any/><text/><data/>
.
As we intend to ignore any order and repetitions
(in contrast with the ordinary XML approach)
this, in fact, means that a sentence (any text data)
is considered rather as an unordered set of words.
•
<tag>...</tag>
transforms to
tag:{...}
and
<tag/>
transforms to
tag:{}
.
•
<tag set:ref="setname1 setname2 ..."/>
transforms to the sequence
tag:setname1, tag:setname2, ...
.
In the case if the element
<tag>
is non-empty with
some content “
...
”, as in the previous clause, we
just add
tag:{...}
to the above sequence.
• Finally, omit
<?xml>
and
<syseqn>
tags.
This way any XML-WDB document with arbitrary
nested XML elements represents system of set equa-
tions with accordingly nested right-hand sides. In par-
ticular, arbitrary XML documents can be incorporated
into our hyperset WDB framework (by nesting in-
side
set:eqn
elements). Both transformations from
XML-WDB to system of set equations and vice versa
have been implemented.
2.3 Distributed WDB
WDB system of set equations may be divided into
several subsystems (XML-WDB files) with the possi-
HYPERSET/WEB-LIKE DATABASES AND THE EXPERIMENTAL IMPLEMENTATION OF THE QUERY
LANGUAGE DELTA - Current State of Affairs
31

bility for the set names s participating in one subsys-
tem to be defined by set equations s = {. . .} in some
other subsystems. To this end we introduce one more
attribute
set:href
(in the same namespace) whose
value should be full set name consisting of a URL of
a possibly remote XML-WDB file concatenated with
#simple-set-name
where
simple-set-name
is the
set:id
value from this file. So, strictly speaking,
we should always assume full set names, even if us-
ing simple set names in set equations of distributed
WDB. This also allows to avoid non-intended simple
set name clashes in different XML-WDB files cre-
ated possibly by various users in remote sites. It is
required that each full set name should refer to an
existing XML-WDB file and corresponding equation
within that file for the simple set name part (after
#
symbol). We also have an appropriate XML schema
(Delta-WDB Site, 2007) for the XML-WDB format.
Of course, the above transformation rules from XML-
WDB to systems of set equations should be amended
accordingly for
set:href
attribute. Anyway, this
will lead to a (possibly huge) unified system of set
equations—distributed WDB.
The analogy of WDB with the WWW does not
imply it is so huge. It could be distributed between
several sites and supported by specialized WDB-
servers of some branches (departments) of an orga-
nization. Another point is that WDB might be much
more structured than the WWW, however the general
approach imposes no restrictions. Nevertheless, the
concept of WDB-schema (much more flexible than
for the relational case and based on the concept of
a bisimulation or “one-way” simulation) relativized
to some typing relation on labels/atomic values can
be considered for such databases ((Sazonov, 1993;
Lisitsa and Sazonov, 1997) and e.g. (Abiteboul et al.,
2000)).
As relational databases are (theoretically) a partial
case of this hyperset approach, it should be straight-
forward to incorporate them into a WDB however het-
erogeneous they might be.
3 QUERY LANGUAGE
There has already been much theoretical consider-
ations on (some versions of) the query language ∆
(Delta) to hyperset/WDB databases. The two main
syntactical categories of Delta are:
• ∆-terms representing set valued operations over
hypersets (set queries); and
• ∆-formulas representing truth valued operations
(boolean queries).
Inclusion of set theoretic operators of transitive clo-
sure (
TC), recursion (Rec), and decoration (Dec)
allows to define in ∆ exactly all polynomial time
computable operations over hypersets (represented as
WDB), thus demonstrating and characterising theo-
retically its rich expressive power (assuming that a
linear order on labels is given). The operators of ∆
are defined as follows:
h∆-termi ::= hset variable or constanti
/
0
{l
1
: a
1
, . . . , l
n
, a
n
} a TC(a) Dec(a,b)
{l : t(x, l) | l : x ∈ a & ϕ(x, l)}
Rec p.{l : x ∈ a | ϕ(x, l, p)}
h∆-formulai ::= a = b
l
1
= l
2
l
1
< l
2
l
1
R l
2
l : a ∈ b ϕ & ψ ϕ∨ ψ ¬ϕ
∀l : x ∈ a.ϕ(x, l) ∃l : x ∈ a.ϕ(x, l)
The intuitive set theoretic semantics of the majority
of the above constructs should be well-understood
by anybody with the minimal mathematical back-
ground in set theory and logic; see also (Sazonov,
2006). General note: a, b, . . . denote (set valued)
terms, x, y, z, . . . are set variables and l, l
i
are label
values (just strings of symbols) or variables, depend-
ing on the context, and ϕ, ψ are (boolean valued) ∆-
formulas. Additionally, the binding label and set vari-
ables l, x, p of quantifiers, collect, and recursion con-
structs above should not appear free in the bounding
term a (denoting a finite set) otherwise these oper-
ators become unbounded and thus, in general, non-
computable. Equality = and the (alphabetic) ordering
< on labels is understood standardly. The relation R
on labels is any (easily) computable relation, in par-
ticular “to be a (prefix/infix/suffix) substring”—quite
usable in queries. It could be also a relation
::
of
typing. For example we could have
John::name
and
June::month
. On the other hand, the equality be-
tween ∆ terms/hypersets a = b (or a ≈ b) is under-
stood as the equality of abstract hypersets denoted by
these terms and, eventually, is computed by the bisim-
ulation algorithm discussed above. Moreover, bisim-
ulation is, in fact, implicitly involved in the (computa-
tional) meaning of the membership relation according
to the equivalence
l : a ∈ b ⇐⇒ ∃m : x ∈ b.(m = l & x ≈ a).
This means: find an outgoing l-labelled edge from b
which leads to some node x bisimilar to a. But think-
ing abstractly, l : a ∈ b says just that a is an l-labelled
element of b. The recursion operator
Rec p.{l : x ∈
a | ϕ(x, l, p)} defines a subset π of the set denoted by
a obtained as the result of stabilizing (due to finite-
ness of a) the monotonic sequence of subsets of a de-
fined iteratively as p
0
=
/
0 and p
k+1
= p
k
∪ {l : x ∈ a |
ICSOFT 2007 - International Conference on Software and Data Technologies
32
ϕ(x, l, p
k
)}. The transitive closure TC(a) denotes the
set of (labelled) elements of elements . . . of elements
of a. We refer to (Aczel, 1988) for the precise defini-
tion of the decoration operator
Dec and only note here
that it is the only operator in ∆ which allows to con-
struct real (cyclic) hypersets like Ω = {Ω} or like in
the Figure 1 from the ordinary “uncycled” sets (of sets
of sets,.. . ) of finite depth. This can be also reason-
ably called the plan performance operator (Sazonov,
2006) because its input(s) can be considered as a plan
of construction of a hyperset, and the output is the re-
sulting abstract hyperset. Imagine that we have a plan
of a Web site (i.e. of a system of hyperlinked Web
pages) and that
Dec is a tool (a query) which auto-
matically creates all the required Web pages.
Practically, constructs of the ∆-query language are
expressed as ‘english-like’ statements in block struc-
tured query language similar to SQL. Additional fea-
tures have been (and even more are intended to be)
added to ∆ making the language more practically con-
venient, but not increasing its theoretical expressive
power. Say, the powerset operation
Pow(a) giving the
set of all subsets of a is evidently intractable (requir-
ing exponential time and space) and is not worth to
be added. But everything which is polynomial time
computable is already definable in the original theo-
retical version of ∆ presented above. Therefore, any
additions we intend to make, however important prac-
tically, are just “syntactic sugaring” of the above the-
oretical version of ∆. In particular, let us note the fol-
lowing extensions:
Library functions: Creation, deletion and modifica-
tion of user defined/predefined queries and con-
stants. These queries/constants can then be used
in any query thus saving time and effort.
Queries with declarations: Similar to the library
function but queries/constants are defined for
(possibly multiple) use within a particular query.
For example, our BNF of ∆ (Delta-WDB Site, 2007)
contains the following production rules:
<set query declaration> ::= "set query "
<set query name> "("[<variables>]")"
(" be " | " = ") <delta-term>
<delta-term with declarations> ::= "let "
<declarations> " in " <delta-term>
" endlet"
Analogously (and even simpler), set constant dec-
larations are quite convenient. Recall that full set
names are typically quite long, having the form
url
#simple-set-name
; thus declaring a set constant,
say c, for this set name will make queries much more
readable and manageable.
3.1 Syntactical Correctness and the
Contextual Analysis
Queries satisfying the BNF are called well-formed.
But they should also be well-typed, with all identifiers
properly declared or quantified The latter is achieved
by tracking and suitably correcting the syntactical cat-
egories and types in the parse tree of a query. This
guarantees that all identifiers are properly declared
and typed (if this is possible at all). Occurrences of
set or label variables or constants, the type of query
declaration and corresponding query calls should mu-
tually agree, etc.
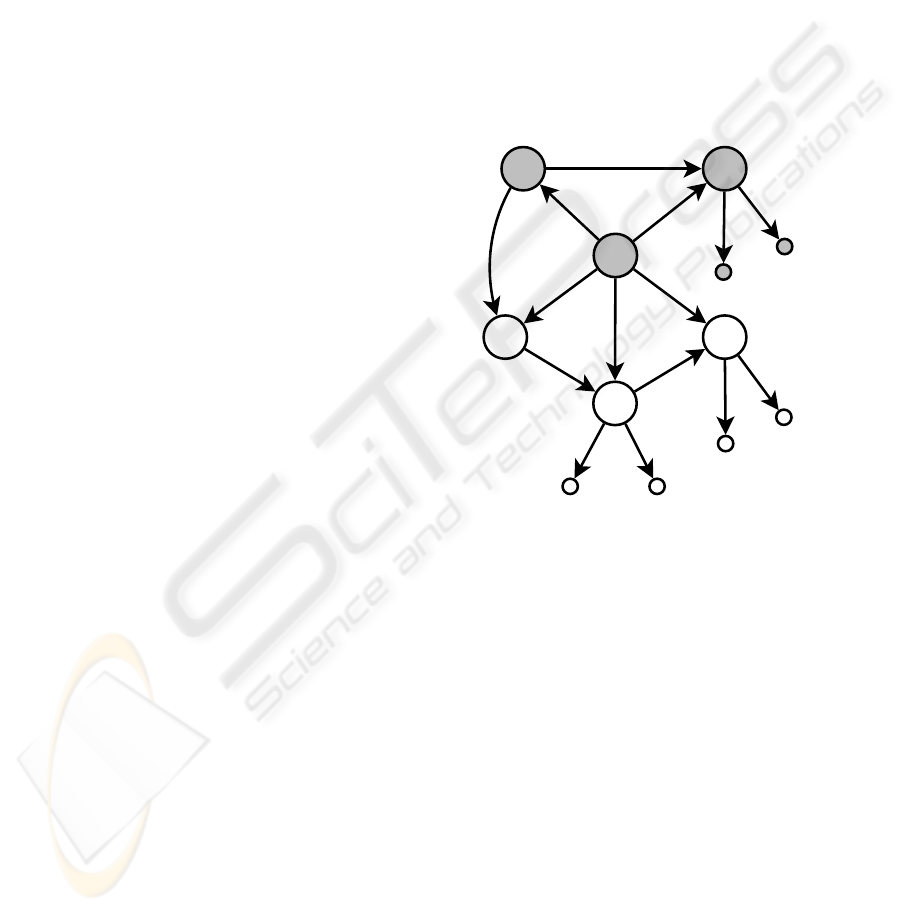
3.2 Example of Non-well-typed Query
BibDB
b2
p1
p2
p3
title
author
bookbook
"Jones"
"Databases"
"Jones"
author
"Databases"
title
refers-to
refers-to
"Smith" "Databases"
author title
refers-to
b1
paper
paper
paper
refers-to
Figure 2: Example of a distributed—according to the
colouring—bibliography WDB (similar to one from (Abite-
boul et al., 2000)) represented as two XML-WDB files with
URL1.
and
URL2
; see (Delta-WDB Site, 2007).
The following is an attempt to query the bibliography
WDB from Figure 2.
> set query collect { pub-type:pub
> where pub-type:pub in BibDB
> and exists ’refers-to’:ref in pub .
> ref=b2 };
Query is well-formed
Query is not well-typed
Error at character 55, occurrence of
identifier name BibDB not declared:
set query collect { pub-type:pub
where pub-type:pub in BibDB <-------
and exists ’refers-to’:ref in pub .
Error at character 104, occurrence of
identifier name b2 not declared:
and exists ’refers-to’:ref in pub .
ref=b2 <-------
HYPERSET/WEB-LIKE DATABASES AND THE EXPERIMENTAL IMPLEMENTATION OF THE QUERY
LANGUAGE DELTA - Current State of Affairs
33

};
Note that
BibDB
and
b2
are identifiers which are
nowhere declared in this query. See the corrected ver-
sion of this example in Section 4.1 where these identi-
fiers are appropriately related to the WDB considered.
4 QUERY EXECUTION
To execute a (set or boolean) well-formed and well-
typed query q whose all participating set names (con-
stants) are taken from the given WDB—a system of
set equations—we should:
extend this system by new equation res = q with res
a fresh (i.e. unused in WDB) set or boolean, if
such is q, name and
simplify the extended system
WDB
′
= WDB+ (res = q)
until it will contain only (possibly nested) bracket
expressions as the right-hand sides of the equa-
tions or the truth values true or false (if the left-
hand side is boolean name).
Thus, after simplification is complete, no complex set
or boolean queries in set equations will appear, and
the resulting version WDB-RES of WDB will con-
sist, alongside with the old equations of the original
WDB, of new set equations (new set names equated
to possibly nested bracket expressions) and boolean
equations (boolean names equated to boolean values
true or false). This process is quite natural. For ex-
ample, if the given query contains some complex sub-
query like q =
q1 then the equation res = q is split
into two subqueries res =
res1 and res1 = q1 with
res1 a fresh set name. We omit further details refer-
ring the reader to (Sazonov, 2006). The point is that
at the end we will have the equation res = {. . .} of the
required form whose right-hand side may use some
set names either from the original WDB or newly in-
troduced during this process auxiliary set names (like
res1 above) with corresponding equations of the re-
quired form. Thus, execution of a query extends the
original WDB to WDB-RES. This extension with the
set name res as the “entrance point” is the result of
the query and can be considered as temporary one un-
til we need this result. (We could also consider update
queries which would change the original WDB.)
It was demonstrated in the op. cit. that ∆ covers the
expressive power of UnQL and UnCAL from (Bune-
man et al., 2000) which also have a polynomial time
complexity, but do not exhaust the full P-time.
4.1 Example of Valid Query and the
Result of its Execution
> set query
> let set constant BibDB be URL1#BibDB,
> set constant b2 be URL2#b2
> in collect { pub-type:pub
> where pub-type:pub in BibDB
> and exists ’refers-to’:ref in pub .
> ref=b2 }
> endlet;
Query is well-formed
Query is well-typed
Result = {paper:URL2#p2, book:URL1#b1}
Finished in: 398 ms
The informal meaning of this query is (imprecisely)
as follows: “Find all publications which refer to the
book
b2
.” But, as we see, the answer contains, be-
sides the evident publication
b1
referring to
b2
, also
p2
which refers to
p3
where the latter is formally
bisimilar to
b2
(same
title
and
author
elements), as
required in the formal query. If we really want to in-
clude only references to the book
b2
, then seemingly
right solution to replace the equality
ref=b2
by the
conjunction
(ref=b2 and book:ref in BibDB)
in
the above query does not really help because in any
case
p3=b2
(are bisimilar) in the above WDB. Equal-
ity of (hyper)sets is defined by their elements, ele-
ments of elements, etc., i.e. by outgoing—not by
incoming—edges. So, after removing redundancies
(say, omitting
p3
) we should have one joint node
b2
with two incoming edges
BibDB
book
−→
b2
and
BibDB
paper
−→
b2
(besides two more incoming
refers-to
edges from
b1
and
p2
and the evident two outgoing
edges). This is probably not what the designer(s) of
this distributed WDB had in mind.
This example emphasizes the real meaning of hy-
perset vs. pure graph approaches to semistructured
databases and the role of removing redundancies on
the level of the design. The right approach here
should be based on a well-chosen discipline:
(i) either to reconstruct this database by replacing la-
bels
book
and
paper
by
publication
and adding
outgoing edges from each publication showing its
type
(
’book’
or
’paper’
; see Figure 3)
(ii) or to use some WDB-schema e.g. requiring that
there is only one, up to bisimulation,
book
/
paper
-
edge from
BibDB
to any given publication.
“Up to bisimulation” means here that if two children
of
BibDB
are bisimilar then they are labelled by the
same label. But it is not our goal here to go into details
of such kind of discipline. In any case, we should
ICSOFT 2007 - International Conference on Software and Data Technologies
34
be precise and accurate in designing the WDB and in
formulating both formal and intuitive versions of our
queries. The mathematical ground of hyperset theory
is quite solid and sufficient for that.
The main point is that if we have a formal query,
it has a unique (up to bisimulation) answer—in fact,
a hyperset or boolean value—and all the queries are
bisimulation-invariant and can be computed in poly-
nomial time (with respect to the size of WDB). Vice
versa, any P-time computable and bisimulation invari-
ant (and also “generic” (Lisitsa and Sazonov, 1997))
query is definable in ∆. In fact, this also assumes
that the language ∆ has full P-time computable power
of restructuring—not only simple retrieval of already
existing elements in the WDB. For example the query
restructuring the
BibDB
database as described in the
previous paragraph in (i) could be written in ∆ using
the plan performance operator Dec.
4.2 Example of Restructuring Query
First, extend the main library by the following useful
queries (defined either formally or—for simplicity of
presentation—semi-formally):
library add
set query Pair(set x, set y) =
{’fst’:x,’snd’:y},
set query First(set z) =
"the first element of z if z is a Pair",
set query Second(set z) =
"the second element of z if z is a Pair",
set query GraphOfPairs(set a) =
"the set of labelled pairs L:Pair(u,v)
where (L:v in u) holds in the
transitive closure TC(a)";
Then the required restructuring query (in (i) above) is
defined as follows:
set query let set constant BibDB = URL1#BibDB
in let set constant restructuredBibDB be
(U collect{
’null’:if (L=’Paper’ or L=’Book’)
then{’publication’:X,
’type’:call
Pair(call Second(X),{L:{}}),
L:call Pair({L:{}}, {})
}
else {L:X}
fi
where L:X in call GraphOfPairs(BibDB)
}
)
in decorate ( restructuredBibDB, BibDB )
endlet
endlet;
Here
’null’
is a label whose value is not impor-
tant,
GraphOfPairs(BibDB)
is essentially the orig-
inal bibliography graph in Figure 2 represented in
the traditional set theoretic way as the set of (or-
dered) pairs, and
restructuredBibDB
denotes the
result of the required restructuring of this graph as set
of pairs. At last,
decorate(restructuredBibDB,
BibDB)
(the plan performance operator applied to the
plan—set of pairs
restructuredBibDB
) essentially
transforms this set of pairs understood as a graph into
corresponding system of set equations (as it is de-
scribed in Section 2) with
BibDB
serving as the main
set name. The content of the set
BibDB
(the result of
this query) is a rather lengthy nested bracket expres-
sion (a set of sets of sets . . .) which is omitted here.
The corresponding graph is as follows:
p3’/b2’
publication
"Jones"
author
"Databases"
title
refers-to
refers-to
"Smith" "Databases"
author title
refers-to
publication
publication
publication
refers-to
"Paper"
"Book"
"Paper"
BibDB’
p2’
"Paper"
type
type
p1’
type
type
"Book"
b1’
type
Figure 3: The result of the restructuring query.
The fact that one publication has the type both of
book
and
paper
is the result of the initial design of
BibDB
.
It is not a failure of the above query.
5 FURTHER EXTENSIONS
5.1 Path Expressions
The ability to select nodes of a WDB graph to arbi-
trary depth can be elegantly achieved using path ex-
pressions. As shown in (Sazonov, 2006), the action of
a rich class of path expressions is definable in the orig-
inal ∆, itself having no path expressions at all, withthe
help of
TC and Rec. Our next goal is to implement the
extension of ∆ by path expressions like in
set query
select {pub-type:x in BibDB
where exists <b1>refers-to*<x>refers-to<b2> .
author:"Smith" in x
};
HYPERSET/WEB-LIKE DATABASES AND THE EXPERIMENTAL IMPLEMENTATION OF THE QUERY
LANGUAGE DELTA - Current State of Affairs
35

Quantification occurs over paths from
b1
to
b2
hav-
ing an appropriate intermediate set/node
x
. Due to
p3
≈
b2
the answer to this query is the non-empty set
{paper:p2}
. It would be empty if to remove “
*
”.
5.2 Supporting Bisimulation/Strong
Extensionality in Background Time
One of the key points of our approach is the inter-
pretation of WDB-graph nodes as set names where
different nodes can, in principle, denote the same (hy-
per)set. Whether it is so is defined by the bisimulation
relation which can be computed by appropriate (re-
cursive) comparison of labelled child nodes. Thus, in
outline, to check bisimulation of two nodes we need
to check bisimulation (or non-bisimulation) between
some children, granchildren, etc. of the given nodes,
i.e. a lot of nodes could be involved. If WDB is dis-
tributed, the communication overhead of download-
ing the relevant XML-WDB files will be too great.
(There is also the analogous problem with
TC, not
discussed here.) So, the equality relation for hyper-
sets seems intractable practically, although theoret-
ically it takes polynomial time with respect to the
size of WDB. Nevertheless, we consider that hyper-
set approach to WDB or semistructured databases is
worth to be implemented because it suggests a very
clear and mathematically well-understood view on
semistructured data and their querying. Thus, the
question is whether bisimulation problem can be re-
solved in any reasonable and practical way. Some
possible approaches and views are outline below.
Firstly, should we expect that in reality bisimilar
nodes in WDB (i.e. redundancies in WDB) will ap-
pear frequently? We could rather assume that WDB is
permanently supported in a strongly extensional state
i.e. with any rare redundancies eliminated.
Redundancies arising during query execution. As
we described above, execution of queries leads to
(temporary) extension of the original WDB poten-
tially leading to new redundancies (so that equal-
ity subqueries applied to newly generated nodes can
be non-trivial). But these redundancies can also be
eliminated locally at the server executing the query.
Moreover, the algorithm of query execution could be
amended in such a way that as soon as a new (aux-
iliary) nodes/set names are generated (like res, res1
in Section 4) any possible redundancies will be elim-
inated immediately.
Let, in general, WDB
′
be an extension of the given
strongly extensional (non-redundant) WDB by a set N
of new set names and by new set equations n = {. . .}
with the right-hand sides involving both old and new
set names. (The original WDB-set equations remain
the same in WDB
′
.) Also, without loss of general-
ity and for the sake of the argument we may consider
that all old and new set equations are flat—involving
no nesting. This is the situation which can arise dur-
ing computation of a query when new set names and
set equations are generated. The question is how to
compute new bisimulation relation ≈
′
on WDB
′
by
using the trivial bisimulation relation coinciding with
identity = on the original WDB. Evidently, ≈
′
re-
stricted to WDB nodes/set names coincide with = on
WDB because set names participating in both parts of
set equations of WDB are also from WDB. (WDB
remains “self-contained”.)
Now, we can conclude from the definition of
bisimulation relation that only those nodes from the
original WDB are needed to compute ≈
′
(between
new nodes and also new vs. old nodes) which are
nodes/set names appearing in the new set equations
and their children. This restricts the number of down-
loaded WDB files, and thus elimination of redundan-
cies can be done almost locally.
Redundancies which can appear during a local up-
date of a WDB file are more problematic because
the old non-bisimilar nodes outside this file might be-
come bisimilar due to possible links (or paths) to the
local nodes with changed/added meaning. The appro-
priate strategy of removing all such redundancies is
not so straightforward (as above) and needs to be de-
veloped yet. However, taking into account the locality
of changes, this task does not seem to be unrealistic.
Local bisimulation. Assume that all WDB nodes are
divided into classes L
i
according to their sites (WDB
servers) or even files. There is a quite natural defini-
tion of local (i.e. computed locally; see (Delta-WDB
Site, 2007)) lower and upper “best” approximations
n
1
≈
L
−
n
2
⇒ n
1
≈ n
2
⇒ n
1
≈
L
+
n
2
to the global bisimulation relation ≈ on the whole
WDB. All these local approximations can help to
compute and to permanently support global bisimu-
lation in a distributed way in background time. More-
over, we could require “local independency” (≈
L
−
=
≈
L
+
, and hence = ≈↾ L) and additionally the “local
non-redundancy” (≈
L
−
= ≈
L
+
= =
L
).
Deliberate redundancies in WDB can also appear,
called mirroring in WWW. But if to require that mir-
roring in WDB should be “officially” registered, then
such a deliberate redundancy should most plausibly
be dealt with in a quite feasible way.
In general, WDB should not be assumed to be just
another version of WWW, freely extensible by any-
body in the world. That is, appropriate discipline
and restrictions in working with WDB could make the
problem of bisimulation practically resolvable.
ICSOFT 2007 - International Conference on Software and Data Technologies
36

6 COMPARISONS
The crucial feature of our approach to semistructured
databases distinguishing it from others such as Lorel
(Abiteboul et al., 1997) and (even the most closest
to our approach) UnQL (Buneman et al., 2000) is its
(hyper)set theoretical character. Also the query lan-
guage ∆ has mathematically precise description of its
expressive power (as P-time) which makes it suffi-
ciently complete from the theoretical point of view.
In this sense our approach is top-down—from theory
to practice.
Some important aspects from the practical point
of view such as path expressions are currently not in-
cluded in the language, unlike the approaches from
op. cit., however being formally definable in the orig-
inal ∆ and pending implementation. As to the UnQL
language and the related language UnCAL, they were
shown to be embeddable in Delta, but not vice versa;
see the technical details in (Sazonov, 2006). In a sense
the same holds for Lorel. (Here we do not take into
account that Lorel was later migrated to the query lan-
guage to XML, where the order plays an essential
role.) The original Lorel deals with graphs, like ∆,
but it considers literal equality between graph nodes
(oids) instead of using bisimulation relation. Lorel
also uses equality between sets of oids, which, how-
ever, is not “deep” set equality assumed by bisimula-
tion. Therefore, Lorel would treat our example with
BibDB
differently, and only very informal comparison
is possible. Thus, Lorel can be said to be also strictly
embeddable in ∆ (ignoring path variables potentially
leading to the exponential complexity and, for sim-
plicity, some aspects like typing and coercion). There
is no recursion operator (except Kleene’s star in path
expressions) and nothing similar to decoration opera-
tor (important for deep restructuring) in Lorel. (How-
ever StruQL can do something reminding decoration;
see e.g. (Abiteboul et al., 2000).) In a sense hyperset
(∆) vs. graph approaches (UnQL and Lorel) compli-
ment each other. Finally, our implementation assumes
distributed WDB, like WWW.
7 CONCLUSION
Although ∆ does not include yet path expressions and
some other useful explicit constructs of the languages
UnQL and Lorel, we already have a working and quite
expressive (in a sense more expressive) query lan-
guage, and this was our current goal. Of course, there
is a lot to do for making this a full-fledged and ef-
ficient (hyper) Set based WDB Management System
(WDBMS or SDBMS).
REFERENCES
Abiteboul, S., Buneman, P., and Suciu, D. (2000). Data on
the Web - From Relations to Semi-structured Data and
XML. Morgan Kaufmann Publishers, San Francisco,
California.
Abiteboul, S., Quass, D., McHugh, J., Widom, J., and
Wiener, J. L. (1997). The Lorel query language for
semistructured data. International Journal on Digital
Libraries, 1(1):68–88.
Aczel, P. (1988). Non-Well-Founded Sets. CSLI, Stanford,
CA.
Barwise, J. (1975). Admissible Sets and Structures.
Springer, Berlin.
Barwise, J. and Moss, L. (1996). Vicious circles: on the
mathematics of non-wellfounded phenomena. Center
for the Study of Language and Information.
Buneman, P., Fernandez, M., and Suciu, D. (2000). UnQL:
a query language and algebra for semistructured data
based on structural recursion. The VLDB Journal,
9(1):76–110.
Codd, E. F. (1983). A relational model of data for large
shared data banks. Communications of the ACM,
26(1):64–69.
Dahlhaus, E. and Makowsky, J. A. (1986). The choice of
programming primitives for SETL-like programming
languages. In ESOP’86, LNCS 213, pages 160–172.
Dahlhaus, E. and Makowsky, J. A. (1992). Query languages
for hierarchic databases. Information and Computa-
tion, 101:1–32.
Delta-WDB Site (2007).
http://www.csc.liv.ac.uk/
˜
molyneux/ICSOFT2007appendix/
.
Leontjev, A. and Sazonov, V. (2001). ∆: Set-theoretic query
language capturing logspace. Annals of Mathematics
and Artificial Intelligence, 33:309–345.
Lisitsa, A. and Sazonov, V. (1999). Linear ordering on
graphs, anti-founded sets and polynomial time com-
putability. Theoretical Computer Science, 224(1–
2):173–213.
Lisitsa, A. and Sazonov, V. Y. (1997). Bounded hyperset
theory and web-like data bases. In Proceedings of the
Kurt Goedel Colloquium (KGC 1997), volume 1234,
pages 178–188.
McHugh, J., Abiteboul, S., Goldman, R., Quass, D., and
Widom, J. (1997). Lore: A database management
system for semistructured data. SIGMOD Record,
26(3):54–66.
Sazonov, V. Y. (1987). Bounded set theory, polynomial
computability and ∆-programming. In Lect. Not.
Comput. Sci., volume 278, pages 391–397.
Sazonov, V. Y. (1993). Hereditarily-finite sets, data bases
and polynomial-time computability. Theoretical Com-
puter Science, 119(1):187–214.
Sazonov, V. Y. (2001). Using agents for concurrent query-
ing of web-like databases via a hyperset-theoretic ap-
proach. In PSI ’02: 4th International Andrei Er-
shov Memorial Conference on Perspectives of System
Informatics, pages 378–394, London, UK. Springer-
Verlag.
Sazonov, V. Y. (2006). Querying hyperset / Web-like
databases. Logic Journal of the IGPL, 14(5):785–814.
HYPERSET/WEB-LIKE DATABASES AND THE EXPERIMENTAL IMPLEMENTATION OF THE QUERY
LANGUAGE DELTA - Current State of Affairs
37
