A CASE STUDY ON THE APPLICABILITY OF SOFTWARE

RELIABILITY MODELS TO A TELECOMMUNICATION

SOFTWARE

Hassan Artail, Fuad Mrad and Mohamad Mortada

Electrical and Computer Engineering, American University of Beirut, Beirut, Lebanon

Keywords: System testing, quality assurance, system reliability, software failures, CASRE (Computer Aided Software

Reliability Estimation), Software Reliability, inter-failure times, Time-Between-Failures.

Abstract: Faults can be inserted into the software during d

evelopment or maintenance, and some of these faults may

persist even after integration testing. Our concern is about quality assurance that evaluates the reliability and

availability of the software system through analysis of failure data. These efforts involve estimation and

prediction of next time to failure, mean time between failures, and other reliability-related parameters. The

aim of this paper is to empirically apply a variety of software reliability growth models (SRGM) found in

the CASRE (Computer Aided Software Reliability Estimation) tool onto real field failure data taken after

the deployment of a popular billing software used in the telecom industry. The obtained results are assessed

and conclusions are made concerning the applicability of the different models to modeling faults

encountered in such environments after the software has been deployed.

1 INTRODUCTION

Test procedures should be thorough enough to

exercise system functions to everyone's satisfaction:

user, customer, and developer. There are several

steps involved in testing a software system. They

comprise unit testing, integration testing, acceptance

testing, and installation testing. If the tests are

incomplete, faults of various types may remain

undetected, while on the other hand, complete and

early testing can help not only to detect faults

quickly, but also to isolate causes more easily

(Pfleeger, 2001).

This paper presents a case study, in which

ftware failures were analyzed after the completion

of the software development and testing phases

before deployment at the customer premises. This

study is different from the traditional software

reliability analysis in the sense that most reported

cases were based on the development and testing

phases or the operational phase, but seldom

considered the software installation and

implementation phases at the client site. Another

important aspect that is taken up in this work is the

examination of the applicability of known software

reliability models to the considered system, given

that such models were primarily developed to handle

reliability analysis during the software testing phase

(typically at the vendor’s site) while assuming fast

error removal.

The studied product is a multi-component billing

soft

ware used by a reputable GSM operator. It

interacts with an Oracle database and with Siemens’

HLR telecommunication systems, and includes

components that use the client/server model to serve

more than 1300 users who access the server from

their Java based client interfaces. It is worth noting

that the vendor’s support team has prior experience

with the implementation of such products in similar

environments, but never with the same combination

of client profile and third party products.

The presented research is based on collected

real life

failure data for a component of the software.

A comparative analysis of the failure data using

various statistical tests was executed in order to

show the statistical model that best-fits this

particular situation. A projection was then made

regarding the underlying component reliability, or in

other words, the maximum allowable execution time

before failing again for a particular fault.

178

Artail H., Mrad F. and Mortada M. (2007).

A CASE STUDY ON THE APPLICABILITY OF SOFTWARE RELIABILITY MODELS TO A TELECOMMUNICATION SOFTWARE.

In Proceedings of the Second International Conference on Software and Data Technologies - SE, pages 178-183

DOI: 10.5220/0001347401780183

 SciTePress

2 PREVIOUS WORK

Since the characteristics of a software system cannot

always be measured directly before delivery, indirect

measures can be used to estimate the system’s likely

characteristics. Several software reliability (SR)

models with basic SR parameters were developed. In

contrast to most reliability models that assume

instantaneous fault removal, Jeske, Zhang, and Pham

(2001) and then Zhang, Teng, and Pham (2003)

stressed that a fault may be encountered more than

once before it is ultimately removed and that new

faults may be introduced to the software due to

imperfect debugging. Mullen (1998) argued that

there is a time lag which most conventional software

reliability models ignore. They considered the fault

removal process with different scenarios using the

state space view of the Non-Homogeneous Poisson

Process (NHPP). Teng and Pham (2002) considered

the error introduction rate and error removal

efficiency as the key measures for reliability growth

across multiple versions of a software system that

was subject to continuous fault removal. The

classical reliability theory was extended in the work

of Goseva-Popstojanova and Trivedi (2000) to

consider a sequence of possibly-dependent software

runs versus failure correlation. A model, suggested

by Singpurwalla (1998), involved concatenating the

failure rate function while assuming that the time to

next failure was greater than the average of past

inter-failure times. Fault removal, repair time, and

remaining number of faults were handled using a

non-homogeneous continuous time Markov chain.

A criterion was proposed by Nikora and Lyu

(1995) for selecting the most appropriate software

reliability model from six models: Jelinski-Moranda,

Geometric, Littlewood-Verral, Musa Basic, Musa-

Okumoto, and NHPP. The goodness-of-fit test based

on the Kolmogorov-Smirnov distance was not

sensitive enough to choose the best model, but it was

used as a preliminary step for filtering unsuitable

ones. Huang, Kuo, Lyu, and Lo (2000) verified that

existing reliability growth models can be derived

based on a unified theory of well-known means:

weighted arithmetic, geometric, and harmonic.

According to Gokhale, Marinos, Lyu, and Trivedi

(1997), commercial software organizations focus on

the residual number of faults as a measure of

software quality. A model was proposed to address

the number of residual defects during the operational

phase. Minyan, Yunfeng, and Min (2000) stressed

that neither practitioners nor experts could choose a

model beforehand since the assumptions of each

model were difficult to prove.

3 CASE STUDY AND APPLIED

RELIABILITY ANALYSIS

Software reliability models can be largely

categorized into two sets: static models where

attributes of the software module are utilized to

estimate the number of defects in the software, and

dynamic models which utilize parametric

distributions and defect patterns to evaluate the end

product reliability. Musa and Okumoto classified

dynamic models in terms of five attributes (Musa,

2004): 1) time, 2) category (number of failures), 3)

type (distribution of the number of failures), 4) class

(functional form of failure intensity in terms of

time), and 5) family (functional form of failure

intensity in terms of expected number of failures).

3.1 Considered Models

The reliability models discussed in this paper are

based on the time domain using either the elapsed

time between failures or the number of failures over

a given period of time. Musa (2004) identified two

sets of reliability models in accordance with time

between failure (TBF) and fault count models. The

first group includes the Jelinski-Moranda, Non-

Homogeneous Poisson Process (NHPP), Geometric,

Littlewood-Verral Quadratic, Littlewood-Verral

Logarithmic, Musa Basic, and Musa Logarithmic.

The second group comprises the Yamada S-Shaped,

NHPP, Schneidewind, Generalized Poisson, and

Brook and Motley’s models.

3.2 System Description

The field failure data are taken from error log files

that date back to the month of February 2006, during

the initial software implementation and integration

of the BSCS version 7 billing software on a

clustered Tru64 Unix platform with an Oracle 9i

RAC database system. The components of the BSCS

billing software are integrated with other third party

interfaces like the HLR system of Siemens and the

Oracle production databases, which include detailed

information and billing data of GSM subscribers.

The connection with Siemens HLR is crucial since it

involves activation of many GSM subscriber

services. The interface with the Oracle database is

equally critical due to the fact that all data are kept

inside various production and rating databases.

Furthermore, these data are accessed from around

1300 concurrent users using either an SQL interface

or Java client programs through a LAN or a WAN.

A CASE STUDY ON THE APPLICABILITY OF SOFTWARE RELIABILITY MODELS TO A

TELECOMMUNICATION SOFTWARE

179

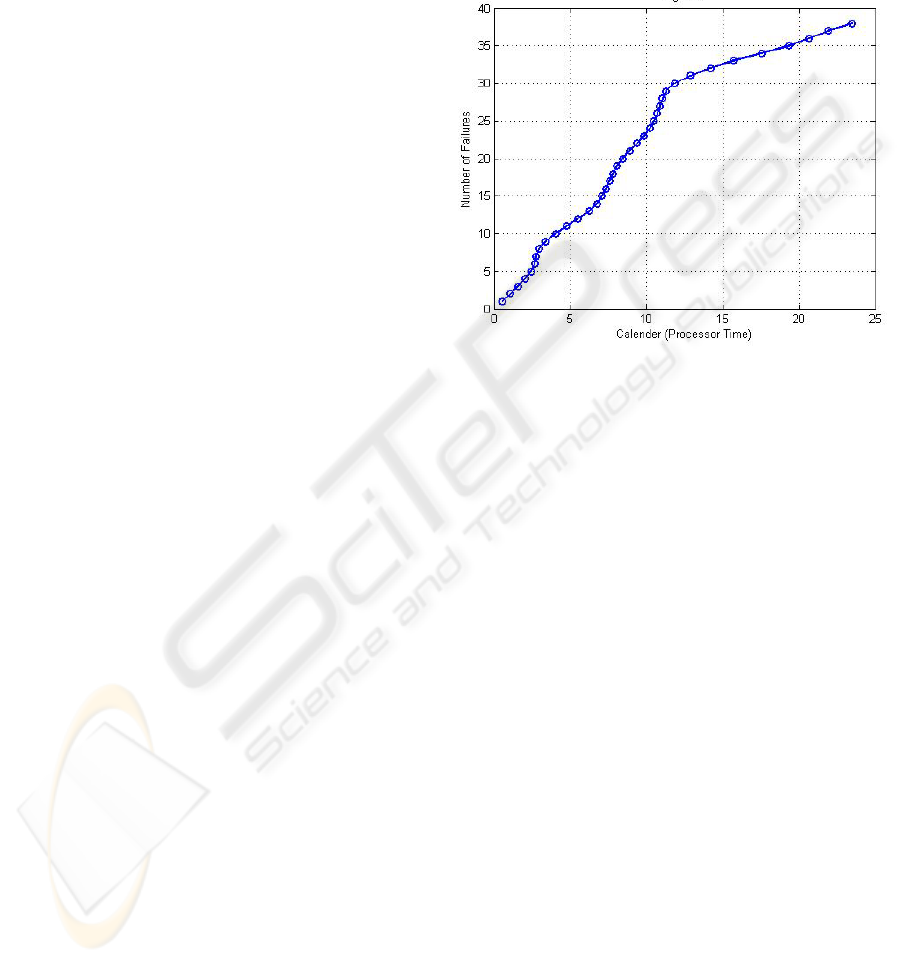
The failure data was examined for any

inherent trend for applicability of software reliability

growth models. This is an important step where the

data content implies either a growth for time-

between-failures or decrease of failure counts as

time progresses. Two data trend tests were used:

running average test and Laplace test. The former

computes the running average of time between

successive failures or count of failures per time

interval. For time between failures, if the running

average increases with failure number, a reliability

growth is implied, while for failure count data, if the

running average decreases with time then reliability

growth is indicated. On the other hand, the Laplace

test computation is based on the null hypothesis that

occurrences of failures can be described as a

homogeneous Poisson process. If the test metric

decreases with increasing failure number, the null

hypothesis is rejected in favor of reliability growth

at an appropriate significance level. Otherwise, the

null hypothesis is rejected in favor of decreasing

reliability (Nikora, 2000).

3.3 Raw Reliability Data Analysis

The cumulative number of 39 failures against their

respective execution times is shown in Figure 1,

where a saturation-like curve behavior is observed.

In the subsequent sections, we divide our execution

time failure data into two sets: time-between-failure

and failure-count sets. This allows for applying a

different set of models for every data type and

having a better view of the reliability of the software

under study. Moreover, our analysis for every data

type- reliability model combination is done using

two estimation methods: maximum likelihood

estimation (MLE) and least squares estimate (LSE).

The choice of the best software reliability model

that mostly fits a particular set of data type, time-

between-failures, or failures count is done using the

following steps (Nikora and Lyu, 1995):

1. Apply a goodness of fit test to determine which

model fits the input data for a specified

significance level.

2. If more than one set of results are a good fit:

a. Choose the most appropriate model(s)

based on the prequential likelihood.

b. In case of a tie, use the model bias trend.

3. If no models provide a good fit to the data:

a. Choose the most appropriate model(s)

based on the prequential likelihood.

b. Use techniques, such as forming linear

combinations of model results or model

recalibration to increase accuracy.

c. Apply the goodness of fit test to the

adjusted model results and identify those

that are a good fit to the data.

4. Finally, the models are ranked using the

CASRE tool according to the following when

applicable: prequential likelihood, Model bias,

Bias trend, Model noise, and Goodness-of-fit.

Figure 1: Cumulative number of failures of PIH

component against processor execution time (hours).

3.4 Time-Between-Failures (TBF)

Figure 2 shows the actual time-between-failure data,

filtered with a Hann window. A running arithmetic

average test showed a reliability growth starting at

failure point 27 and onwards. The Laplace test

showed the software starting to exhibit reliability

growth at the 5% significance level until about the

34th failure, at which point the Laplace test statistic

assumes a value less than -1.64495. The inserted

failure data set into the CASRE software tool

consisted of 38 data points. For the purpose of this

test, the CASRE tool was set with a data range from

27 to 35 time-between-failures data points with the

models parameters estimation end point at 30, i.e.

training the models parameters from data range 27-

30 before fixing them. The number of steps past the

last data point in the modelling range, for which

predictions are made, is selected to be 4. This way,

one could see how close are each model’s first 3

failure data predictions to the true ones and look into

the next future failure time and reliability.

ICSOFT 2007 - International Conference on Software and Data Technologies

180

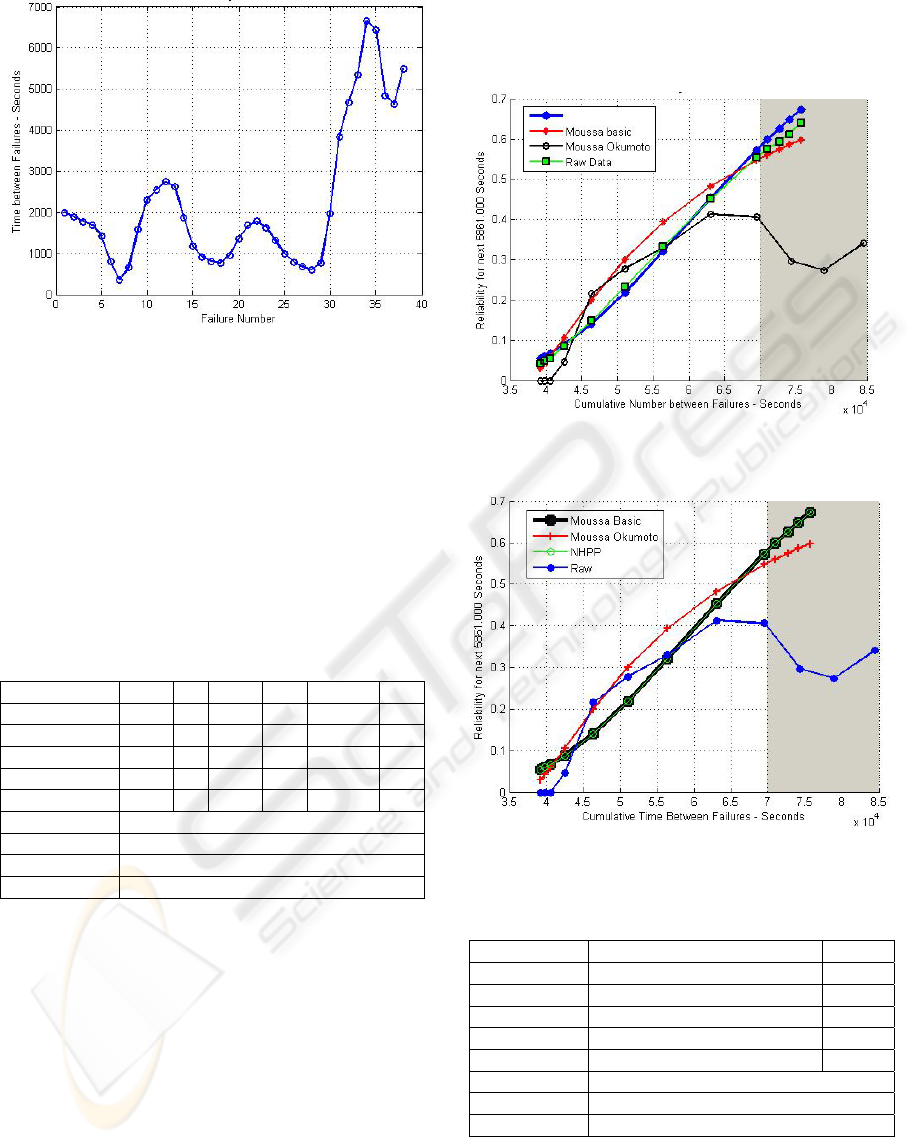
Figure 2: Filtered raw data plot for TBF.

3.4.1 TBF Analysis with the MLE Method

Table 1 is obtained after running the CASRE

software tool with the selected models. The

goodness of fit test is done first to determine which

models are fit to the data. We consider the first three

ranked reliability models and displayed their various

estimates and predicted outputs. The top three fitting

models in this case were: Musa-Okumoto, ULC, and

Musa basic. They are ranked according to their

Kolmogorov-Smirnov (KS) distance test value.

Table 1: Model goodness of fit for TBF using MLE.

Model -In PL Bias Trend Noise Distance Rank

Musa-Okumoto 39.28 0.52 0.34 1.27 0.42 1

ULC 39.51 0.48 0.36 1.13 0.38 2

Musa Basic 40.03 0.46 0.34 1.39 0.29 3

NHPP (TBE) 40.03 0.46 0.34 1.39 0.29 4

MLC 40.03 0.46 0.39 0.07 0.29 5

DLC/S/4 Did not fit data at given significance level

ELC Did not fit data at given significance level

Geometric Did not fit data at given significance level

Quadratic LV Did not fit data at given significance level

Figure 3 shows the fits of three top-ranked reliability

models onto the actual TBF data, where the models’

estimates are plotted in the shaded region.

3.4.2 TBF Analysis with LSE Method

The information in Table 2 is obtained after running

the CASRE software tool with the selected models.

Out of the models that pass the fit test, we consider

the Musa Basic, NHPP, and Musa-Okumoto models.

As implied in the data in Table 2, the bias,

prequential likelihood, and relative accuracy are not

computed when employing the least squares

estimation method. Figure 4 presents the fit of the

three models onto the actual data points. Similar to

the MLE case, the estimates of the software

reliability models are plotted in the shaded region.

Figure 3: Models' estimated and predicted reliability for

TBF using MLE.

Figure 4: Models estimated and predicted reliability for

TBF using LSE.

Table 2: Model goodness of fit for TBF using LSE.

Model Distance Rank

Musa Basic 0.29 1

NHPP (TBE) 0.29 2

MLC 0.29 3

ULC 0.38 4

Musa-Okumoto 0.42 5

ELC Did not fit data at given significance level

Quadratic LV Did not fit data at given significance level

Geometric Did not fit data at given significance level

3.5 Failure Counts (FC)

Figure 5 shows the Laplace test results illustrating

reliability growth at the 5% significance level until

A CASE STUDY ON THE APPLICABILITY OF SOFTWARE RELIABILITY MODELS TO A

TELECOMMUNICATION SOFTWARE

181

about the 13th failure, at which the Laplace test

assumes a value less than -1.64495.

Figure 5: Laplace trend test on raw data for FC

The failure count data set into the CASRE software

tool consists of 18 data points. For this test, the tool

was set up with a data range from 1 to 15 failure-

count data points, with the models parameters

estimation end point at 12. This implies that the

models’ parameters were trained from the first 12

data points before fixing them. The number of steps

past the last data point in the modelling range, for

which predictions are to be made, is selected to be 4.

We can see how each model’s first 3 failure data

predictions came close to the true ones and also look

into the next future failure count and reliability.

3.5.1 FC Analysis with MLE Method

Table 3 is obtained after running the CASRE

software tool with the selected software reliability

models specific to the failures count case, which

divides the x-axis into equal interval of time with a

length of 1.389 hours. The fit test is done first in

order to determine which models best fit the actual

real field failure data. We then considered the three

reliability models that passed the test, as shown in

the table. It is noted that the ranking was done in

accordance with the Chi-Square (χ

) value where by

smaller values led to a higher ranking.

As was done earlier, we illustrate the outcome

of the fit test against the raw data in Figure 6.

Table 3: Fit results for FC using MLE. χ

denotes Chi-

Square and the fourth column stands for significance level.

Model

5% Fit? Sig. (%) Rank

Gen. Poisson 10.16 No 3.78 --

NHPP (intervals) 5.49 Yes 24.04 1

Schick-Wolverton 10.16 No 3.78 --

Schneid.-Cum. 1st 31.34 No 0.0 --

Schneidewind:all 5.49 Yes 24.04 2

Yamada S-Shaped 8.31 Yes 8.93 3

Figure 6: Estimated/predicted reliability for FC using

MLE.

3.5.2 FC Analysis with the LSE Method

Table 4 applies to the failure count case that divides

the x-axis into equal interval of time with a length of

1.389 hours per interval. The three top passing

models from the fit test are illustrated in the table:

Generalized Poisson, Schick-Wolverton, and

Schneidewind: all. The ranking was performed

according to the value of the Chi-Square test value,

with a smaller value leading to a higher ranking.

Table 4: Goodness of fit results for FC using LSE.

Model

5% Fit? Sig. (%) Rank

Gen. Poisson 5.38 Yes 25.05 1

NHPP (intervals) 10.85 No 2.83 --

Schick-Wolverton 5.38 Yes 25.05 2

Schneid.-Cum. 1st 31.34 No 0.0 --

Schneidewind:all 5.93 Yes 24.04 3

Yamada S-Shaped 8.08 Yes 8.93 4

The fit of the three-ranked reliability models onto

the actual failure data is illustrated in Figure 7, and

where the models’ data point estimates are plotted in

the shaded region.

ICSOFT 2007 - International Conference on Software and Data Technologies

182

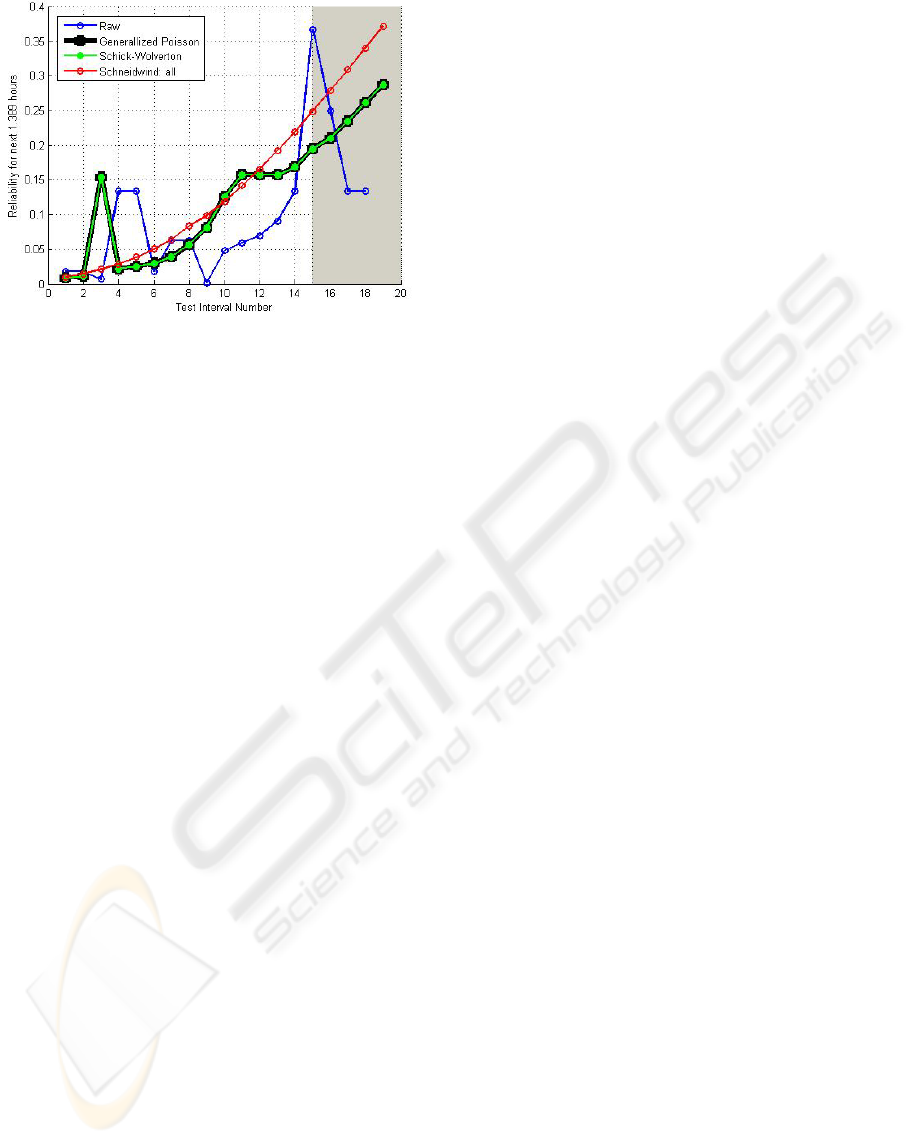
Figure 7: Estimated/predicted reliability for FC using LSE.

4 CONCLUSIONS

Although some reliability models fitted well the

time-between-failure data, all considered models

with both maximum likelihood (MLE) and least

squares (LSE) methods did not initially pass the

goodness-of-fit test when applied to the whole range

of the non-filtered data. Existing reliability models

considered fault removal upon detection and hence,

could not initially be suitable for our application

since the detected faults were never removed during

software installation and integration. The developers

actually worked around these faults to decrease their

frequency of occurrence, until it was time for the

next patch that dealt specifically with these faults.

Based on our findings, it is preferable to stick to

the software reliability growth models (SRGM)

dealing with failure counts and use the least square

estimation (LSE) method. The prequential likelihood

test can not be obtained when using the LSE

method, so instead, the Chi-Square test was

performed. The Generalized Poisson SRGM exhibits

a better fitness over all the other models, like the

Musa Okumoto, Musa Basic, and NHPP models. In

fact, when comparing the predictions of the four

reliability modules, we can see that the Generalized

Poisson predicted more faithfully the software

reliability than the other three models. For instance,

to achieve a 30% reliability of the software, the

implementation and integration phase should run for

around 15.27 hours in case of both Musa-Okumoto

and Musa Basic models, for around 22.5 hours in

case of Non-Homogeneous Poisson Process

(NHPP), and for around 26.39 hours in case of the

Generalized Poisson model. Moreover, the LSE

method performs much better when compared with

MLE in the short data range. Hence, the least square

estimation method adapts faster than the maximum

likelihood estimation method on a small range of

failure data points. However, on the long run, MLE

performs better than LSE if the failure data range

increases considerably.

REFERENCES

Gokhale, S., Marinos, P., Lyu, M., Trivedi, K., 1997.

Effect of Repair Policies on Software Reliability,

12th

Annual Conference on Computer Assurance, IEEE

Computer Society.

Goseva-Popstojanova, K., Trivedi, K., 2000. Failure

Correlation in Software Reliability Models. IEEE

Transactions on Reliability, 49(1),

pp. 37-48.

Huang, C., Kuo, S., Lyu, M., Lo, H., 2000. Quantitative

Software Reliability Modeling from Testing to

Operation. 11th International Symposium on Software

Reliability Engineering,

IEEE Computer Society.

Jeske, D., Zhang, X., Pham, L., 2001. Accounting for

Realities when Estimating the Field Failure Rate of

Software. 12th International Symposium on Software

Reliability Engineering,

IEEE Computer Society.

Minyan, L., Yunfeng, B., Min, C., 2000. A Practical

Software-Reliability Measurement Framework Based

on Failure Data. International Symposium on Product

Quality and Integrity,

IEEE Computer Society Press.

Mullen, R., 1998. The Lognormal Distribution of Software

Failure Rates: Application to Software Reliability

Growth Modeling. 9th International Symposium on

Software Reliability Engineering,

IEEE Computer

Society

Musa, J., 2004. Software Reliability Engineering: More

Reliable Software Faster and Cheaper. McGraw-Hill,

edition.

Nikora, A., Lyu, M., 1995. An Experiment in Determining

Software Reliability Model Applicability, 6th

International Symposium on Software Reliability

Engineering

, IEEE Computer Society.

Nikora, A., 2000. Computer Aided Software Reliability

Estimation User’s Guide, available online at:

http://www.openchannelfoundation.org/projects/

CASRE_3.0

Pfleeger, S., 2001. Software Engineering. Prentice Hall.

Singpurwalla, N., 1998. Software Reliability Modeling by

Concatenating Failure Rates, 9th International

Symposium on Software Reliability Engineering, IEEE

Computer Society

Teng, X., Pham, H., 2003. A Software-Reliability Growth

Model for N-Version Programming Systems. IEEE

Transactions on Reliability, 51(3),

pp. 311-321.

Zhang, X., Teng, X., Pham, H., 2001. Considering Fault

Removal Efficiency in Software Reliability

Assessment. IEEE Transactions on Systems, Man, and

Cybernetics – Part A, 33(1),

pp. 114-120.

A CASE STUDY ON THE APPLICABILITY OF SOFTWARE RELIABILITY MODELS TO A

TELECOMMUNICATION SOFTWARE

183