
A META-MODEL FOR REQUIREMENTS VARIABILITY ANALYSIS
Application to Tool Generation and Model Composition
Bruno Gonzalez-Baixauli, Miguel A. Laguna
Departamento de Inform
´
atica, Universidad de Valladolid, Campus Miguel Delibes, 47011 Valladolid, Spain
Julio Cesar Sampaio do Prado Leite
Departamento de Inform
´
atica, PUC-Rio, Marqu
ˆ
es de S
˜
ao Vicente, 225, G
´
avea - Rio de Janeiro, RJ - Brasil - 22453-900
Keywords:
Meta-model, goal-oriented, requirements engineering, aspect-oriented, model composition, modeling tools.
Abstract:
Variability analysis techniques have an important drawback: the analysis of Non-Functional Requirements.
Usually, these techniques do not fully deal with them and only mention that they should be considered. In
our framework, we use an intentional model-based approach where the functional models are used to define
the variability space and the non-functional models are the criteria for choosing a variant. We found two
problems using this approach: a) integration of functional and non-functional models, and b) scalability due
to the number of variants. Our proposed solution is to use ideas from aspect oriented software development.
Therefore, we use aspectual relationships to relate functional and non-functional models, and we obtain a better
separation of concerns that allows scalability to be improved. In this paper we define the meta-model to set
the modeling language used by our framework, and we show how meta-models can be applied to: a) generate
modeling environments (using a meta-modeling tool); and b) define rules to describe model transformations.
Model transformations are used to compose aspectual models creating new models.
1 INTRODUCTION
Recently, interest in software variability has been
growing. This interest is based on the necessity to
provide higher levels of functionality, extensibility
and adaptability of the software product to improve
its competitivity, as in Software Product Lines. This
problem was initially dealt with in design, searching
for the mechanism to allow its implementation, but
without studying its necessity. Analyzing the vari-
ability from the requirements analysis viewpoint al-
lows this necessity to be studied, under the premise
that the sooner the variability is detected, the bet-
ter it can be dealt with. There are several propos-
als in this subject, using feature models (Kang et al.,
1990), use-cases (Halmans and Pohl, 2003), or both
(Griss et al., 1998). In any case, there is an im-
portant drawback in all of them; they do not deal
with the analysis of Non-Functional Requirements
(NFR). This limitation is very important, even more
than in traditional software, because NFR are one
of the main causes of variability, e.g. different se-
curity levels. In our approach, we propose the use
of techniques from Requirements Engineering (RE),
specifically from goal-oriented (GO) approaches, to
variability. Goal-oriented RE proposes an intentional
analysis of requirements, which (among other things)
allows a more natural study of alternatives and to
analyze the impact on NFR using the NFR Frame-
work (Chung et al., 1999). Also, its application to
variability has already been explored successfully in
(Gonzalez-Baixauli et al., 2004; Yijun et al., 2004),
which use functional goals to define the variability
space, and softgoals to select alternatives.
We have found some problems using goal mod-
els: a) the integration of functional and non functional
models; b) a combinatorial explosion in the num-
ber of variants to analyze. The first problem is due
to operationalizations, i.e. functional elements that
solve, to some degree, the NFR. These functional el-
ements are inside non-functional models, and there is
no mechanism to integrate them into functional ones.
Thus, all elements are usually modelled in a unique
model. The second problem is because each variation
produces a combinatorial increment of the variants,
therefore even simple models have a great number of
291
Gonzalez-Baixauli B., A. Laguna M. and Cesar Sampaio do Prado Leite J. (2007).
A META-MODEL FOR REQUIREMENTS VARIABILITY ANALYSIS - Application to Tool Generation and Model Composition.
In Proceedings of the Second International Conference on Software and Data Technologies, pages 291-297
DOI: 10.5220/0001348502910297
Copyright
c
SciTePress

them (Gonzalez-Baixauli et al., 2004).
The solution we propose is to apply ideas from
aspect-oriented (AO) approaches (Kiczales et al.,
1997), specifically from the early stages techniques
(early-aspects (Brito and Moreira, 2004)). To solve
the integration, we use an aspectual relationship that
allows each concern to be put into separate models,
and composition rules to generate new models in-
tegrating the operationalizations into the functional
model. This separation into models solves the prob-
lem, but it requires a definition of the way they are
composed. We get a higher scalability since we can
make local selections in models before they are com-
posed, and we can compose only the models we are
interested in.
This proposal is part of our on-going requirements
variability analysis using the stakeholders’ goals and
desires. In this article we focus on the first step: the
definition and description of the modeling elements
by means of a meta-model and the definition of the
composition rules. There are several proposals taking
into account goal models, but inside agent-oriented
approaches as reported by Susi et Al. (Grau et al.,
2006). These proposals usually use the meta-model
only to specify elements and relationship, but (Susi
et al., 2005) apply it to develop a tool in Eclipse. We
focus on GO modeling, and clarify their concepts by
simplifying them and defining the meta-model (Sec-
tion 2). Then, in Section 3 we apply the meta-model
to generate a modeling framework; and to the defini-
tion of the composition rules (Section 4). Finally, in
Section 5, the conclusions and future work are set.
2 META-MODEL FOR
VARIABILITY ANALYSIS
In this Section we define the elements, relationships
and constraints of these models using a meta-model.
The initial premises were to allow:
1. The modeling of fundamental GO concepts.
2. The relating of functional models and the opera-
tionalizations (solutions) of non-functional mod-
els.
3. The modularizing of models using two mecha-
nisms: a classical one, where a model can refer
to another one as part of the main model; and an-
other aspectual, i.e. the NFR solutions that affect
functional elements.
4. The generating of new models as a composition
of previous models, whose elements and relation-
ships reference the original models.
SOFTGOAL
GOAL
TASK
decomposition
contribution (+ or -)
operationalization
GOAL
GOAL
SOFTGOAL
TAS
K
Figure 1: Elements and relationships of the V-Graph lan-
guage. Adapted from (Yijun et al., 2004).
5. The modifying (deleting) of elements and rela-
tionships of combined models (e.g. to select an
alternative) without affecting the original models.
With these premises in mind, the main design de-
cisions are:
Concerning the modeling of GO concepts
(Premise 1), we take as our source the components of
the V-Graph language (Yijun et al., 2004). Figure 1
shows the model elements and relationships adapted
to our proposal. The elements are Goals to achieve,
Softgoals to satisfy (in some degree), and Tasks that
solve Goals or Softgoals. The differences with respect
to the original model are in the relationships that, as
shown in (da Silva, 2006), have several problems of
understandability. So we rename the previous Corre-
lation relationship Contribution (with types Make and
Help if positive, and Break and Hurt if negative), and
we split the Contribution relationship, used originally
to relate Task to Goals and Softgoals, into Decompo-
sition (types And, Or, and Xor) for Goals and Opera-
tionalizations (types WeakOp and StrongOp) for Soft-
goals. Note the differences between Decomposition
and Operationalizations, although both have the idea
of giving a more specific solution, the second allows
us to go from the fuzzy nature of softgoals to the clear
satisfaction of tasks with a certain degree (it is at the
same time a decomposition and a positive contribu-
tion).
Another important difference with respect to the
V-Graph is that we introduce the idea of models, al-
lowing the definition of different concerns separately.
Hence, initial elements are grouped into GO models
called Concerns, defined as a hierarchical decomposi-
tion from a root element, that represents the Concern.
To solve the problem of relating functional and
non-functional models (Premise 2), we use an aspec-
ICSOFT 2007 - International Conference on Software and Data Technologies
292
tual based relationship (AO Relationship). It models
how an NFR (represented by a softgoal) can affect a
functional element. Therefore, if we want to take into
account the NFR, the solutions of the softgoal (Op-
erationalization in NFR Framework notation) should
be included in the functional model as possible de-
compositions of the functional element. We use here
a simple approach where the tasks operationalizating
the softgoal are added to the functional part as alterna-
tive solutions, focusing on increasing the model vari-
ability.
With modularizing (Premise 4), the aspectual
mechanism is obtained by the AO Relationship, and
the composition rules (see Section 4). As for the
“classical” mechanism, we take advantage of the fact
that Concerns are represented by the root element.
Therefore, we implement this modularization allow-
ing the use of hierarchical relationships (decomposi-
tion or operationalization) to relate concerns elements
and root elements of other models. This represents
the model of the root element as part of the main
model. Note that this relationship type relates ele-
ments owned by different models. While this is not a
problem defining the meta-model, it will cause prob-
lems in tool generation that can be solved using refer-
ences to elements as shown in the next Section.
As for composed models, we define a new meta-
class: ComposedModel, whose components are ref-
erences to elements and relationships defined in the
Concerns, but also new elements/relationships. The
references are generated by composition, and can be
deleted without affecting the sources (Premises 4 and
5).
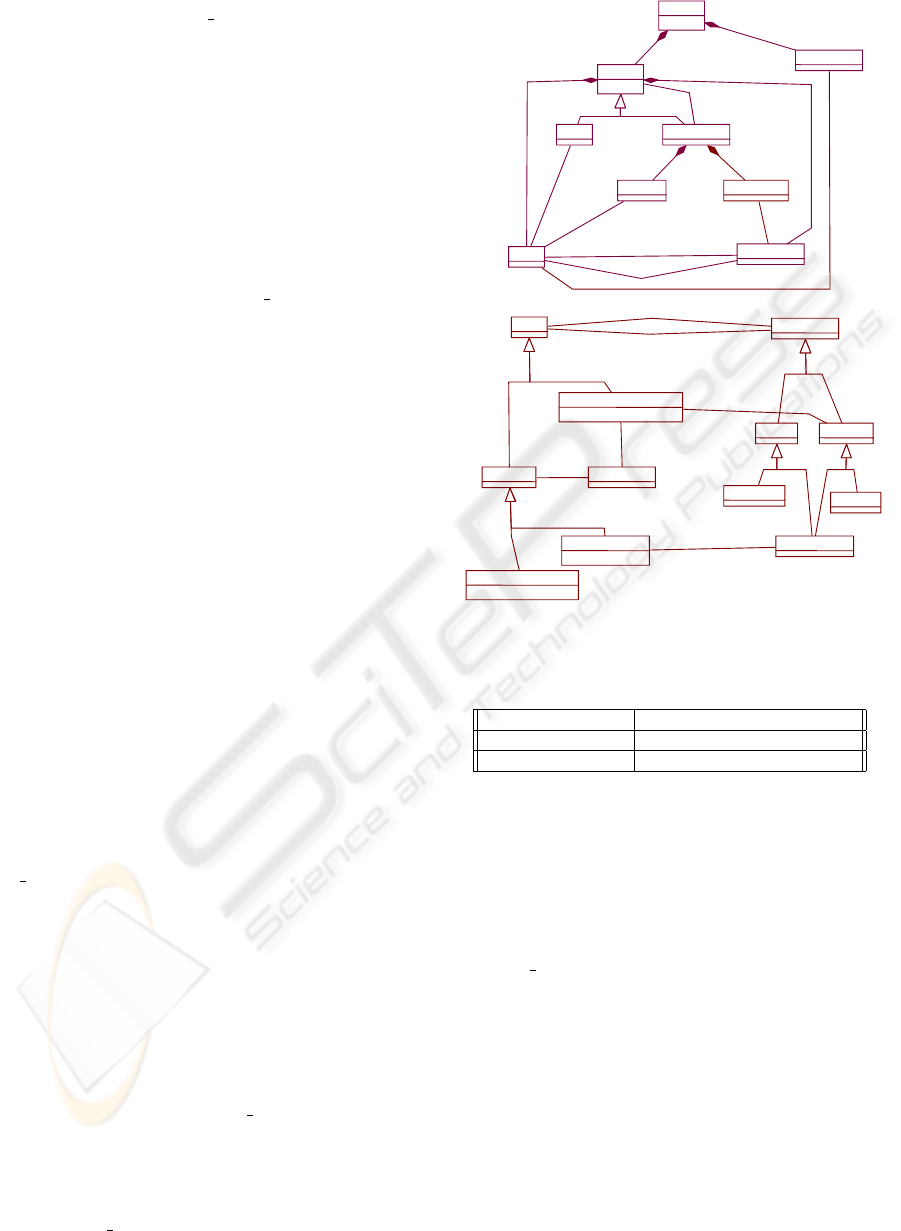
The metamodel in Fig. 2 is the result of these de-
cisions. Part a) shows the main meta-classes and rela-
tionships: we introduce the idea of Project to group
Models and aspectual relationships between them
(AO Relationships). There are two kinds of models
required by modularization: Concerns, where GO el-
ements and relationships are modeled (explained in
Fig. 2b)); and ComposedModels that are generated
from one or two models, and that are composed of
element and relationship references (ElementRef and
RelationshipRef respectively), and possible new ele-
ments/relationships generated by the composition.
In Fig 2b) the GO elements and the relationships
in Fig. 1 are defined. The target and source associ-
ations between Element and GO Relationship are re-
fined by sub-types constraining the kind of elements
that can be related by each one. Element is refined
in soft (Softgoal) and hard elements (HardElements)
with a clear distinction of satisfaction, i.e. Goal and
Task. The GO Relationship is refined in Hierarchy,
which expresses the refinement of elements, and Cor-
Project
name: String
Model
1..*
AO_Relationship
A)
Concern
0..1
ComposedModel
Model
name: String
+sourceModel
*
1..2
+createdBy
0..1
1..*
+/root
1
+source
1
*
GO_Relationship
Element
ElementRef
+referredElem
1
0..*
1..*
RelationshipRef
+referredRel
1
0..*
*
GO_Relationship
Element
+source1
*
+target1
*
+target
1*
Element
*
B)
Correlation
Softgoal
softSatisfaction: SoftSatisfactionKind
+correlated {subset target}
1
+source
1
Hierarchy
HardElement
Decomposition
Contribution
AO_Relationship
+source
*
+target
1
*
Task
isVariantMember: boolean
Goal
satisfaction: HardSatisfactionKind
Operationalization
+ solution {subset source}1
Figure 2: Meta-model classes and relationships.
Table 1: Subtypes of GO relationships.
Decomposition And, Or and Xor
Operationalization WeakOp and StrongOp
Contribution Make, Help, Hurt and Break
relation which defines how elements affect softgoals.
Decomposition and Contribution are the main types
of Hierarchy and Correlation respectively. Opera-
tionalization is considered to be a hierarchy since it
provides possible solutions to softgoals, but also as a
Correlation, because it affects the softgoal satisfac-
tion. GO Relationships sub-classes are abstract since
there is another inheritance level (not shown in the fig-
ure) described in Table 1. Decomposition targets and
sources are defined by means of an OCL constraint
because it is easier than defining it as specifics rela-
tionships (it relates elements of the same kind or goals
with tasks). A more detailed description can be found
in (Gonzalez-Baixauli, 2006).
2.1 Example
To illustrate the use of the meta-model and the com-
position, we apply them to an example. The cho-
A META-MODEL FOR REQUIREMENTS VARIABILITY ANALYSIS - Application to Tool Generation and Model
Composition
293
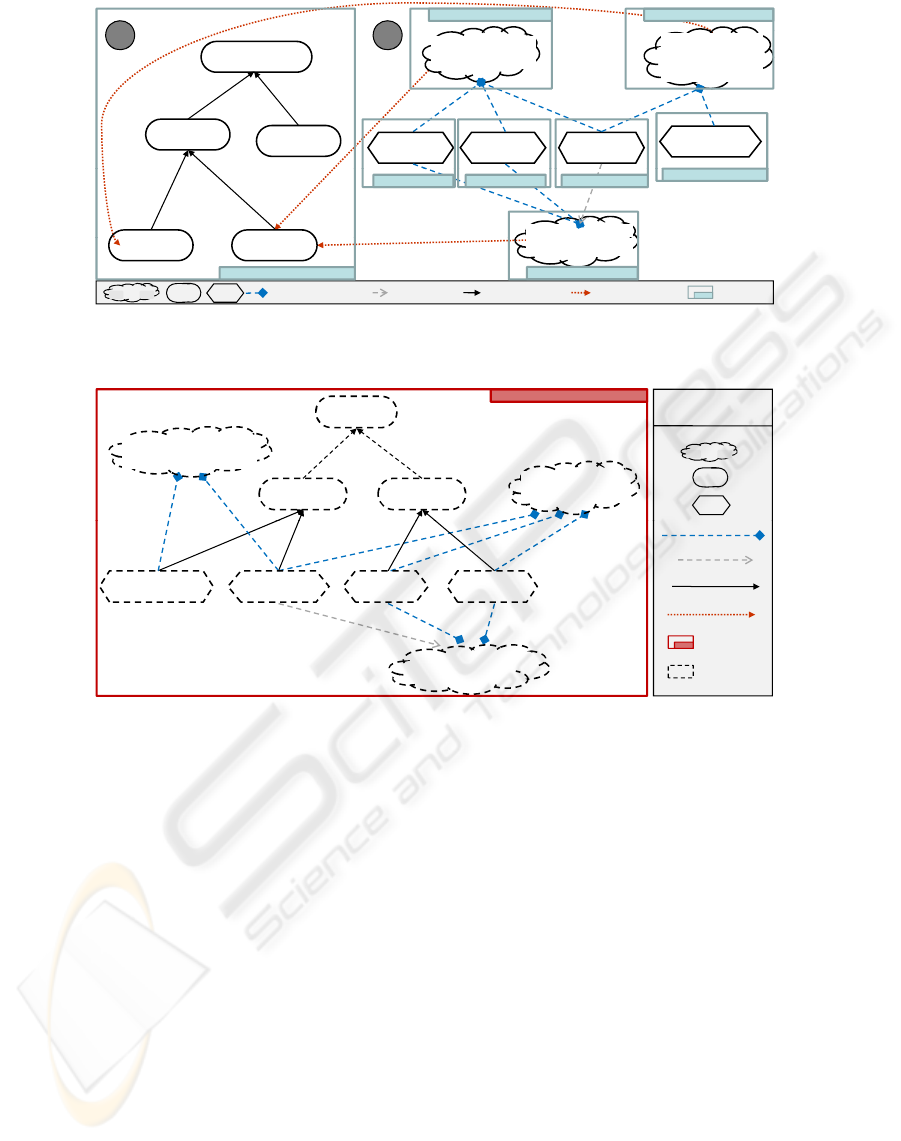
b
Adaptable [Input. …] Adaptable [Compose. …]
a
b
Communicate
[Message]
Adaptable [Input,
Motor Disability]
Adaptable
[Compose,
Mental Disability]
And And
+ +
+
+
+
Emit
[Message]
Receive
[Message]
Use [Input,
Buttons]
Use [Input,
Sweep]
Use [Voice
Recognition]
Use [Compose,
PCS]
And And
+ +
+
+
+
+
Input
Compose
A
da
p
table
[
In
p
ut
,
+
+
--
Use [Compose, …]
Use [Voice, …]Use [Input, …]Use [Input, …]
Goal
Concern
Operationalization
Decomposition AO RelationshipContribution
Input
[Message]
Compose
[Message]
p[p,
Speech Disability]
Task
Communicate [Message]
Adaptable [Input, …]
Softgoal
Figure 3: Concern examples for AAC domain. Each concern is in separated boxes. Part a) shows the functional one, and b)
several softgoals (NFR) and their solutions.
Emit
[Message]
And And
A
da
p
table
[
Com
p
ose
,
Emit [Message] {composed}
Legend
Softgoal
Input
[Message]
Compose
[Message]
Or
Or
+
++
Or
Or
p[p,
Mental Disability]
Adaptable [Input,
Motor Disability]
Goal
Task
Softgoal
Use [Input,
Btt ]
Use [Input,
S]
Use [Voice
Riti]
Use [Compose,
PCS]
Or
Or
+ ++
Or
Or
Operationalization
Decomposition
Contribution
Adaptable [Input
B
u
tt
ons
]
S
weep
]
R
ecogn
iti
on
]
PCS]
++
--
Composed
Model
AO Relationship
Adaptable
[Input
,
Speech Disability]
Reference
Figure 4: Partial model composed from the concerns of Fig. 3.
sen application domain is Alternative & Augmenta-
tive Communicators (AAC), i.e. tools that allow peo-
ple with disabilities to communicate. Our choice of
this domain is based on its high variability.
Figure 3 shows some concerns (represented as
boxes) for the domain in the same figure. Part a)
describes a simple functional model where the main
goal is to communicate a message (Communicate
[Message]), decomposed into several sub-goals. Fig-
ure 3b) shows some of the domain softgoals, and
their solutions. The NFR analysis focuses on soft-
goal Adaptability that represents how easy the system
is to use for certain disabilities. Note that tasks are
usually represented as new concerns, this is because
they are the solution to several softgoals, so they can-
not be part of them. Finally, AO relationships (red
dotted lines) describe how softgoals affect functional
elements.
Figure 4 shows an example of a ComposedModel,
resulting from the successive composition of the mod-
els in Fig. 3. This new model includes references to
the elements of the concerns. Both figures are similar,
but the first shows seven different models that are sep-
arated, while the second shows a single model where
non-functional solutions are integrated with the func-
tional elements (new Or decompositions), and the el-
ements are references to the source elements.
3 APPLICATION TO TOOL
GENERATION
We apply the meta-model to generate a modeling en-
vironment using the meta-modeling tool named GME
(Generic Modeling Environment) (Vanderbilt Univer-
sity (Nashville), 2007). We use GME because it is
easy to use, and freely available. But we need to make
some modifications to our meta-model, because the
tool M2-model is not MOF. The differences between
the M2-models are mainly that GME uses some extra
classes to represent graphical concepts, marked with
ICSOFT 2007 - International Conference on Software and Data Technologies
294

Table 2: Changes to meta-model in Fig. 2 to adapt to GME M2-model.
Meta-model class GME Implementation
Models Class with stereotype <<Model>>
Project Model which contains the other models
Elements Class with stereotype <<Atom>>
Associations Classes with stereotype <<Connection>> and special elements
named connectors attached to Connection and meta-classes to
be connected
References Class with stereotype <<Reference>> linked to referred metaclass
Figure 5: Screenshot of the modeling environment generated with GME.
stereotypes. These changes are indicated in Table 2
An important question is how to associate ele-
ments in different models. To relate elements of dif-
ferent concerns (i.e. when one concern is a sub-model
of another concern, and when one element contributes
to a softgoal of another concern) we use another ele-
ment reference (named OtherModelElement Ref ) that
refers to the other concern element, and is different
from ElementRef (part of the original meta-model).
As for about AO Relationships, since they are owned
by Project, they can use the port feature of GME mod-
els, i.e. models are represented in the Project window
as boxes with the elements inside (but not the rela-
tionship) what can be linked.
GME allows the figures that represent each ele-
ment to be customized. Figure 5 shows a screen-
shot of the resulting tool with the models in Fig. 3
and 4. Several models are in the figure: the model
in the upper-left window is the project model, where
the boxes are the models (red for concerns and yel-
low for composed models), the elements are ports on
boxes, and the lines are the AO relationships. The
right-hand windows are the concerns in Fig. 3, and
lower-left window is the composed model in Fig. 4.
The boxed elements are references, both to refer ele-
ments from other models as to represent ElementRef.
Another advantage of this tool is that it provides
OCL constraints, and allows the project to be ex-
ported to XML. A drawback here is that exportation
is done using the tool meta-model (e.g. with meta-
classes connection), not as instances of the defined
meta-model classes. This implies that the models
need to be converted to apply the rules defined in the
next Section.
4 APPLICATION TO
COMPOSITION
A second direct application of the meta-model is the
definition of model compositions. Concerns allow
separated system parts of interest to be defined, but we
A META-MODEL FOR REQUIREMENTS VARIABILITY ANALYSIS - Application to Tool Generation and Model
Composition
295
CM: ComposedModelM_Source:Model
+sourceModel
M_Target:Model
+sourceModel
M_Source:Model M_Target:Model
<<new>>
<<new>>
E_Source: Element
+source
E Target: Element
+target
+target
E_Source: Element
+source
E Target: Element
+target
CMOrRel: Or
E_Target: Element
+target
<<new>>
g
E_Target: Element
+target
AOR: AO_Relationship
<<new>>
AOR: AO_Relationship
EOper: Element
+source
Oper: Operationalization
+source
EOper: Element
Oper: Operationalization
+source
E_TargetetORrel.targCMwnerOR/ORrel.o:relOR
=
∧
=
¬∃
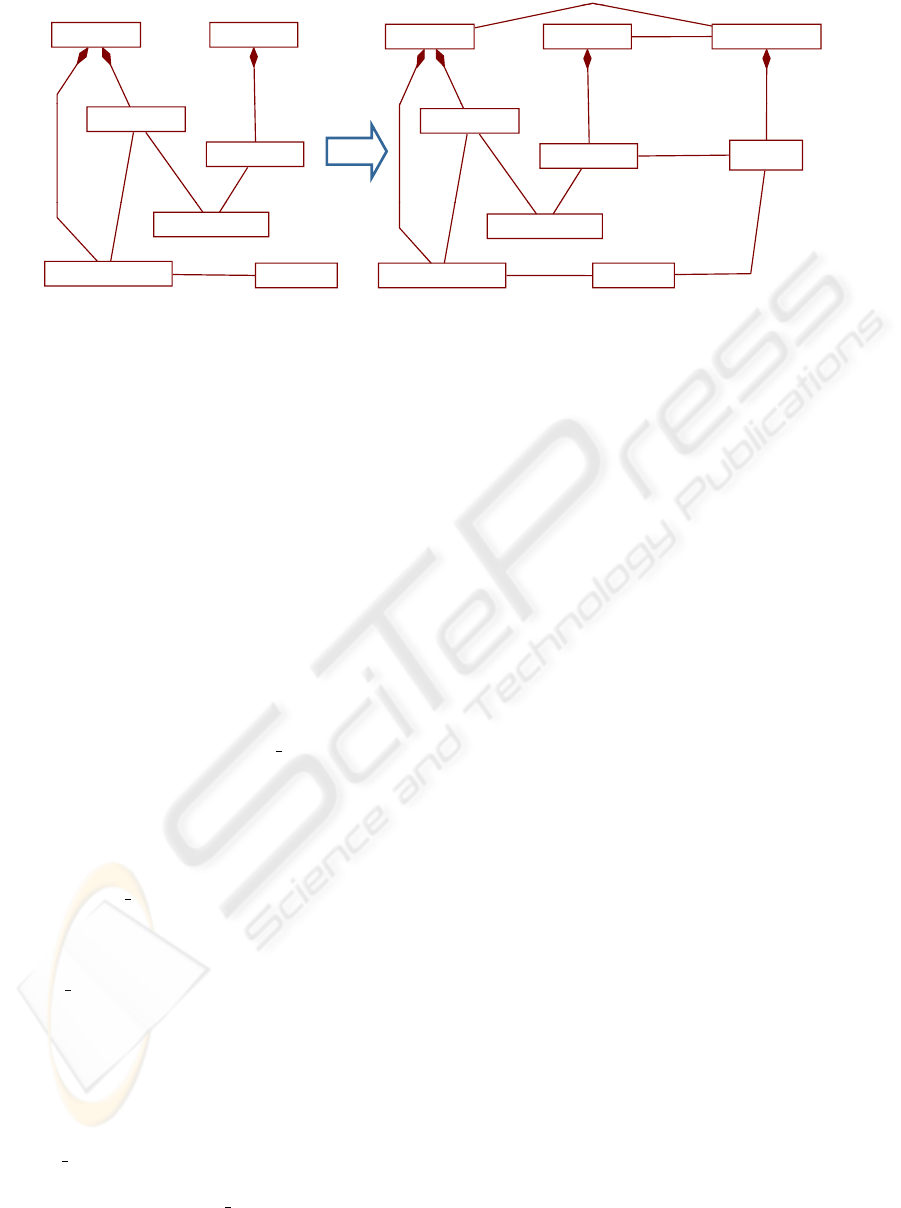
Figure 6: Composition rule example (Rule 3.1).
need to compose these parts to obtain a classical GO
model where existing techniques can be used to ana-
lyze the system. We define composition rules using
model transformations, which are based on instances
of the meta-model elements. These rules transform
a Project to obtain a modified Project with the new
ComposedModel. Hence, the transformation source
and target are defined over the same meta-model, and
rules are successively applied over the result of pre-
vious rules as done in graph transformation. In our
approach the composition is fairly simple:
1. A new model is created (instance of Composed-
Model), owned by the Project and linked to the
source models (sourceModel relationship).
2. References to Elements and GO Relationships in
the source models are created, and they are linked
to the original ones. Note that this is done for
elements/relationships, but also for references to
them, but new references must refer to the origi-
nal elements/relationships.
3. For each AO Relationship between elements of
source models, new relationships (instances of
Or decomposition) are created. They link oper-
ationalizations of the source softgoal to the target
of AO Relationships.
Figure 6 shows an example of a composition rule
definition. This rule corresponds to the third step: it
creates a new OR relationship when an AO relation-
ship exists between two elements of the input mod-
els (each one in a different model), and when there
is no OR relationship decomposing to the target el-
ement (E Target) in the new model (ensured by the
constraint). In this case, one of the operationaliza-
tions of the source element (E Source) is added to the
new relationship. To complete the composition an-
other rule is needed (numbered 3.5) which adds all
the other softgoal operationalizations to the OR re-
lationship. Constraint ensures the rule is only ex-
ecuted when there is already no OR relationship in
the model. The complete definition can be found in
(Gonzalez-Baixauli, 2006).
We implemented these rules using XML
stylesheets (XLST), that take the project repre-
sented in XML, the models to be composed and the
name of the new model, and return a new XML file
with the project containing the new model. Note that
to integrate this implementation with the modeling
environment it is necessary to convert the model in
the GME M2-model to our model, what is also done
using XLST.
5 CONCLUSIONS AND FUTURE
WORK
In this work, we show a meta-model that describes
the elements of our proposal for requirements vari-
ability analysis based on goal models and aspects.
The meta-model definition includes GO modeling el-
ements, separation into different models, AO con-
structs, and variability analysis relationships.
Our approach has advantages both for variability
analysis, as for a more general application of goal
models, such as: improving the separation of con-
cerns; allowing functional and non-functional mod-
els to be integrated; and improving the scalability of
satisfaction analysis. Better separation of concerns
also leads to a higher reuse if the concerns are general
enough, for example using NFR Catalogs as proposed
in the NFR Framework (Chung et al., 1999).
Concerning future work, this is a first step in our
framework for variability analysis. We intend to adapt
our previous work in variability selection (Gonzalez-
ICSOFT 2007 - International Conference on Software and Data Technologies
296

Baixauli et al., 2004) to this new framework and the
AO paradigm. New examples will be worthy for eval-
uating the composition mechanism, and the model-
ing approach. Finally, even though the tool used
allows simple models to be created, and to easily
change the meta-model, that makes it very useful for
prototyping, we find some drawbacks, such as the
limited customization, the complex extension mech-
anism (e.g. to link with other tools), and the require-
ment of the main program (GME), only for Windows
platform. Therefore, we are working on a new tool
using Eclipse and the GMF project, that will give sup-
port to the complete framework.
REFERENCES
Brito, I. and Moreira, A. (2004). Integrating the NFR frame-
work in a RE model. In Early Aspects 2004: Aspect-
Oriented Requirements Engineering and Architecture
Design, pages 27–32.
Chung, L., Nixon, B. A., Yu, E., and Mylopoulos, J. (1999).
Non-Functional Requirements in Software Engineer-
ing, volume 5. Springer.
da Silva, L. F. (2006). An aspect-oriented requirements
modeling strategy. PhD thesis, Departamento de In-
formatica, PUC-Rio. in Portuguese.
Gonzalez-Baixauli, B. (2006). Meta-modelo para el an
´
alisis
de variabilidad guiado por metas. Technical report,
Grupo GIRO. Universidad de Valladolid.
Gonzalez-Baixauli, B., Leite, J., and Mylopolous, J. (2004).
Visual Variability Analysis for Goal Models. In RE
2004, pages 198–207, Kyoto, Japan. IEEE Computer
Society.
Grau, G., Cares, C., Franch, X., and Navarrete, F. (2006). A
comparative analysis of i* agent-oriented modelling
techniques. In SEKE 2006, San Francisco, CA, USA.
Griss, M., Favaro, J., and d’Alessandro, M. (1998). Inte-
grating Feature Modeling with the RSEB. In ICSR5,
pages 76–85, Vancouver, BC, Canada.
Halmans, G. and Pohl, K. (2003). Communicating the Vari-
ability of a Software-product Family to Customers.
Journal Software and Systems Modeling, 2(1):15–36.
Kang, K., Cohen, S., Hess, J., Novak, W., and Peterson, S.
(1990). Feature-Oriented Domain Analysis (FODA)
Feasibility Study. Technical Report CMU/SEI-90-
TR-21.
Kiczales, G., Lamping, J., Mendhekar, A., Maeda, C.,
Lopes, C. V., Loingtier, J.-M., and Irwin, J. (1997).
Aspect-oriented programming. In European Confer-
ence on Object-Oriented Programming, ECOOP’97,
volume 1241 of LNCS, pages 220–242, Jyv
¨
askyl
¨
a,
Finland. Springer-Verlag.
Susi, A., Perini, A., Mylopoulos, J., and Giorgini, P. (2005).
The tropos metamodel and its use. Informatica,
29:401–408.
Vanderbilt University (Nashville) (2007).
Generic modeling environment (gme 6).
http://www.isis.vanderbilt.edu/projects/gme/. Date
retrieved: April 18, 2006.
Yijun, Y., Leite, J. C. S. d. P., and Mylopoulos, J. (2004).
From goals to aspects: discovering aspects from re-
quirements goal models. In RE 2004, pages 33–42.
A META-MODEL FOR REQUIREMENTS VARIABILITY ANALYSIS - Application to Tool Generation and Model
Composition
297
