MECHANICAL SYSTEM MODELLING OF ROBOT DYNAMICS

USING A MASS/PULLEY MODEL

L. J. Stocco and M. J. Yedlin

The Department of Electrical and Computer Engineering, The University of British Columbia

2332 Main Mall, Vancouver, BC, Canada, V6T 1Z4

Keywords: Mass matrix, inertia matrix, MP model, pulley, differential transmission, mechanical system representation,

robot dynamics, impedance, equivalent electric circuit.

Abstract: The well-known electro-mechanical analogy that equates current, voltage, resistance, inductance and capacitance

to force, velocity, damping, spring constant and mass has a shortcoming in that mass can only be used to simulate

a capacitor which has one terminal connected to ground. A new model that was previously proposed by the

authors that combines a mass with a pulley (MP) is shown to simulate a capacitor in the general case. This new

MP model is used to model the off-diagonal elements of a mass matrix so that devices whose effective mass is

coupled between more than one actuator can be represented by a mechanical system diagram that is

topographically parallel to its equivalent electric circuit model. Specific examples of this technique are

presented to demonstrate how a mechanical model can be derived for both a serial and a parallel robot with both

two and three degrees of freedom. The technique, however, is extensible to any number of degrees of freedom.

1 INTRODUCTION

The concept of impedance and its generalization

reactance, has been used to define equivalent

circuits of mechanical and electro-mechanical

systems since the development of the Maxwell

model of solids. The idea that driving point

impedances could be decomposed into terms that

parallel electrical elements was initiated by (Foster,

1924) who showed that the frequency response of

any system is determined by the poles and zeros of

its transfer function. The conditions for network

synthesis are described by (Brune, 1931) and later

applied by (Paynter 1961) who introduced bond

graphs to distinguish and represent effort and flow

variables in a graphical setting. Examples of

electro-mechanical system simulations are

numerous and include magnetic circuits (Hamill,

1993), mechatronics and electromechanical

transducers (Tilmans, 1996), (van Amerongen &

Breedveld, 2003), (Sass et al., 2004).

Mechanical block diagrams are routinely used

to model robot dynamics although some (Eppinger

& Seering, 1992) limit them to a single axis while

others (Yamakita et al., 1992) rely entirely on

equivalent electric circuits to avoid the inherent

difficulties of creating mechanical models of multi-

axis devices, transmission systems or other systems

with coupled dynamics.

Section 2 of this paper describes the

conventional electro-mechanical analogy and points

out a limitation of the mass model. It goes on to

describe a new mass/pulley (MP) model which

overcomes the inherent deficiency in the

conventional mass model. In Section 3, it is shown

how the new MP model can be used to model the

dynamics of devices which have coupled effective

masses. Examples are provided which include both

2-DOF and 3-DOF serial and parallel manipulators.

Lastly, concluding remarks are made in Section 4.

2 ELECTRO-MECHANICAL

ANALOGIES

The ability to define an electro-mechanical

equivalent circuit stems from the parallelism in the

differential equations that describe electrical and

mechanical systems, each of which involve an

across variable, a through variable and an

impedance or admittance variable. In electrical

circuits, voltage

E(s) is the across variable and

current

I(s) is the through variable. In mechanical

systems, velocity

V(s) is the across variable and

force

F(s) is the through variable (i.e. flow variable

J. Stocco L. and J. Yedlin M. (2007).

MECHANICAL SYSTEM MODELLING OF ROBOT DYNAMICS USING A MASS/PULLEY MODEL.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 25-32

DOI: 10.5220/0001614400250032

 SciTePress

(Fairlie-Clarke, 1999)). This results in a

correspondence between resistance

R and damping

B, inductance L and spring constant K, and

capacitance C and mass M shown in (1-3). An

alternate approach treats force as the across variable

and velocity as the through variable but that approach

is not used here. By (1-3), the electromechanical

equivalents shown in Figure 1 can be substituted for

one another to model a mechanical system as an

electrical circuit and vise versa.

Figure 1: Admittance of electro-mechanical equivalents.

2.1 Classical Mass Model Limitation

Each of the components in Figure 1 has two

terminals except for the mass which has only one.

This is due to the fact that the dynamic equation of a

mass (3) does not accommodate an arbitrary

reference. Acceleration is always taken with respect

to the global reference, or ground. Consider the two

systems in Figure 2 which are well known to be

analogous.

Figure 2: LC circuit and mechanical equivalent.

In Figure 2, the voltage across the capacitor

corresponds to the velocity of the mass v. Both of

these are relative measurements that only correspond

to one another because both are taken with respect to

ground. Consider, on the other hand, the circuit in

Figure 3 which contains a capacitor with one

terminal open circuited.

Figure 3: RC circuit and mechanical equivalent.

In Figure 3, the capacitor carries no current

and therefore, has no effect on the output voltage e

In other words, the voltages at n

and n

are equal so

the capacitor behaves like a short circuit. In the

mechanical “equivalent”, it is not possible to

connect a non-zero mass M to node n

without

affecting the output velocity v

. This is due to the

implicit ground reference of the mass (shown by a

dotted line) which prevents it from ever behaving

like a mechanical short circuit. Note that this same

limitation does not apply to the spring or damper

since they both act as a mechanical short circuit

(infinitely stiff connection) if one terminal is left

unconnected, just like their electrical counterparts,

the inductor and resistor.

2.2 The Mass/Pulley (MP) Model

Because of the above limitation, there are

mechanical systems which can not be modelled

using a mechanical system diagram. Elaborate

transmission systems such as robotic manipulators

may contain mass elements that are only present

when relative motion occurs between individual

motion stages. Currently, systems such as these can

only be modelled using electric circuits since

capacitors can be used to model this type of

behaviour but masses cannot.

It would be useful to have a mechanical

model which simulates the behaviour of a capacitor

without an implicit ground connection so that any

mechanism (or electric circuit) could be modelled by

a mechanical system diagram. This new model

should have two symmetric terminals (i.e. flipping

the device over should not affect its response), obey

Ohm’s Law, and be able to accommodate non-zero

velocities at both terminals simultaneously. A model

proposed by the authors (Stocco & Yedlin, 2006)

combines a mass with the pulley-based differential

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

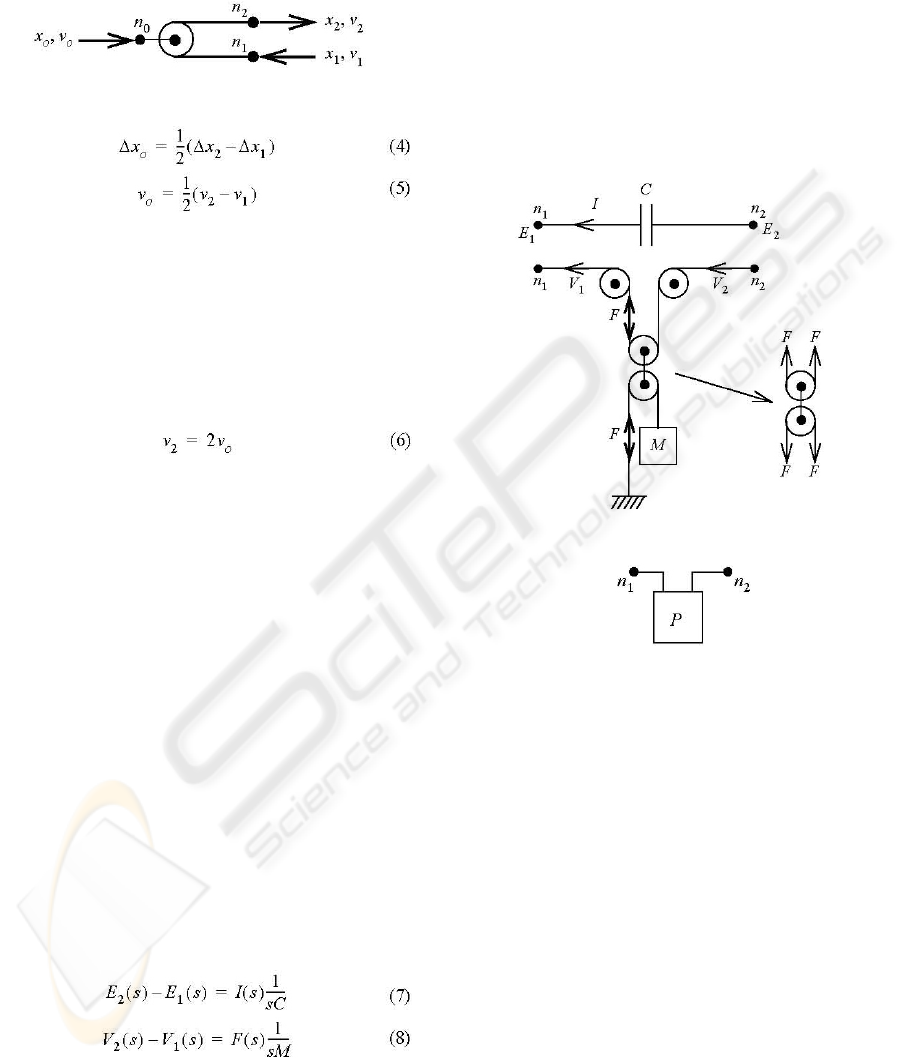
transmission shown in Figure 4. The pulley system

obeys the differential position / velocity relationship

shown in (4,5).

Figure 4: Pulley based differential transmission.

Note from (5) that although the pulley

provides the desired differential velocity input, it

also introduces an undesired 2:1 reduction ratio.

However, setting v

to 0 (i.e. connecting n

ground) results in (6). Therefore, a similar pulley

system with one input tied to ground could be used

to scale up velocity by an equivalent ratio.

The double pulley system shown in Figure 5

is a differential transmission with a unity gear ratio.

The primary pulley provides the differential input

while the secondary pulley cancels the reduction

ratio to achieve unity gain. A mass connected to the

secondary pulley is accelerated by a rate equal to the

difference between the acceleration of the two

inputs, n

and n

. This system simulates the

behaviour of a capacitor that may or may not be

connected to ground (Figure 5). Voltage E

corresponds to velocity V

, voltage E

corresponds to

velocity V

, current I corresponds to tension F and

capacitance C corresponds to mass M as shown by

(7,8). Note that the free-body diagram of the centre

pulley shows that the tension F in the primary cable

is equal to the tension F in the secondary cable. The

system must be balanced because any net force on

the massless centre pulley would result in infinite

acceleration of the pulley and therefore, the mass as

well.

The MP model uses ideal cables with zero

mass and infinite length and stiffness. The ideal

cables travel through the system of massless,

frictionless pulleys without any loss of energy. The

MP model operates in zero gravity so the mass is

only accelerated as a result of cable tension and/or

compression. Unlike practical cables, the ideal

cables never become slack. When an attractive force

is applied between n

and n

, F<0 and the mass is

accelerated downward. A block diagram of the MP

model is presented in Figure 6 where P has the same

value as M in Figure 5. Note that, unlike a pure

mass, the MP model has two terminals, n

and n

which correspond to the two ends of the primary

cable.

Figure 5: Mass / pulley equivalent of a capacitor.

Figure 6: Block diagram of MP model.

Consider Figure 7 which is the mechanical

system from Figure 3 with the mass replaced by an

MP model. With terminal n

left unconnected, the

primary cable of the MP model travels freely

through the primary pulley without accelerating the

mass or consuming energy. The MP model behaves

like a mechanical short circuit, just like the capacitor

in Figure 3. Also note the topological similarity

between the electrical circuit in Figure 3 and its true

mechanical equivalent in Figure 7. This is a direct

result of the topological consistency between the

capacitor and the MP model, both of which have two

symmetric terminals. As pointed out in (Stocco &

Yedlin, 2006), this consistency allows one to

analyze mechanical systems using electric circuit

analysis techniques once all masses have been

replaced by MP models.

MECHANICAL SYSTEM MODELLING OF ROBOT DYNAMICS USING A MASS/PULLEY MODEL

Figure 7: Mechanical equivalent using MP model.

3 ROBOT MASS MATRIX

Consider the simplified dynamics of a 2-DOF robot

(9) where M is the mass matrix, B is the damping

matrix, F is a vector of joint forces/torques (10), R is

a vector of joint rates r

and r

(10), and s is the

Laplace operator. Spring constants, gravitational and

coriolis effects are assumed to be negligible for the

purpose of this example. If the damping in the

system is dominated by the actuator damping

coefficients, B is a diagonal matrix (10). M, on the

other hand, represents the effective mass perceived

by each joint and is not diagonal or otherwise easily

simplified in general.

For simple kinematic arrangements such as

the redundant actuators shown in Figure 8 which

only have a single axis of motion, M is shown in

(11). The system responses are modeled by the

mechanical system diagram shown in Figure 9 and

the dynamic equation shown in (10). Using the

electromechanical transformation described in

Section 2, this system can also be represented by the

electrical circuit analogy shown in Figure 9.

Performing nodal analysis on the circuit in

Figure 9 results in (12) by inspection. Note however,

that (12) contains the term i

-i

as well as v

which

corresponds to the end-point velocity in the

mechanical system or, in other words, the sum of the

joint rates r

. To obtain a correspondence between

electrical and mechanical component values, the

dynamic equation (10) is rearranged in (13) where

the associated damping

B' and mass M' matrices are

shown in (14,15). From (14), the resistor

admittances g

and g

and capacitor values c

and c

correspond to the equivalent damping and mass

values

, b'

, m'

and m'

(16) respectively.

Figure 8: Redundant rotary & prismatic actuators.

Figure 9: System models of redundant actuators.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

In this simple example, masses are sufficient

to model the system behaviour but only because the

device has a single degree of freedom so

M' is

diagonal and there is no cross-coupling between

actuators. In general, however, effective mass is not

always decoupled and the off-diagonal elements of

M' can be expected to be non-zero. When M' is not

diagonal, conventional single-terminal masses are

unable to model the entire effective mass of the

system. They can not model the off-diagonal terms

that describe inertial effects resulting from relative

motion of the actuators.

3.1 Serial 2-DOF Robot

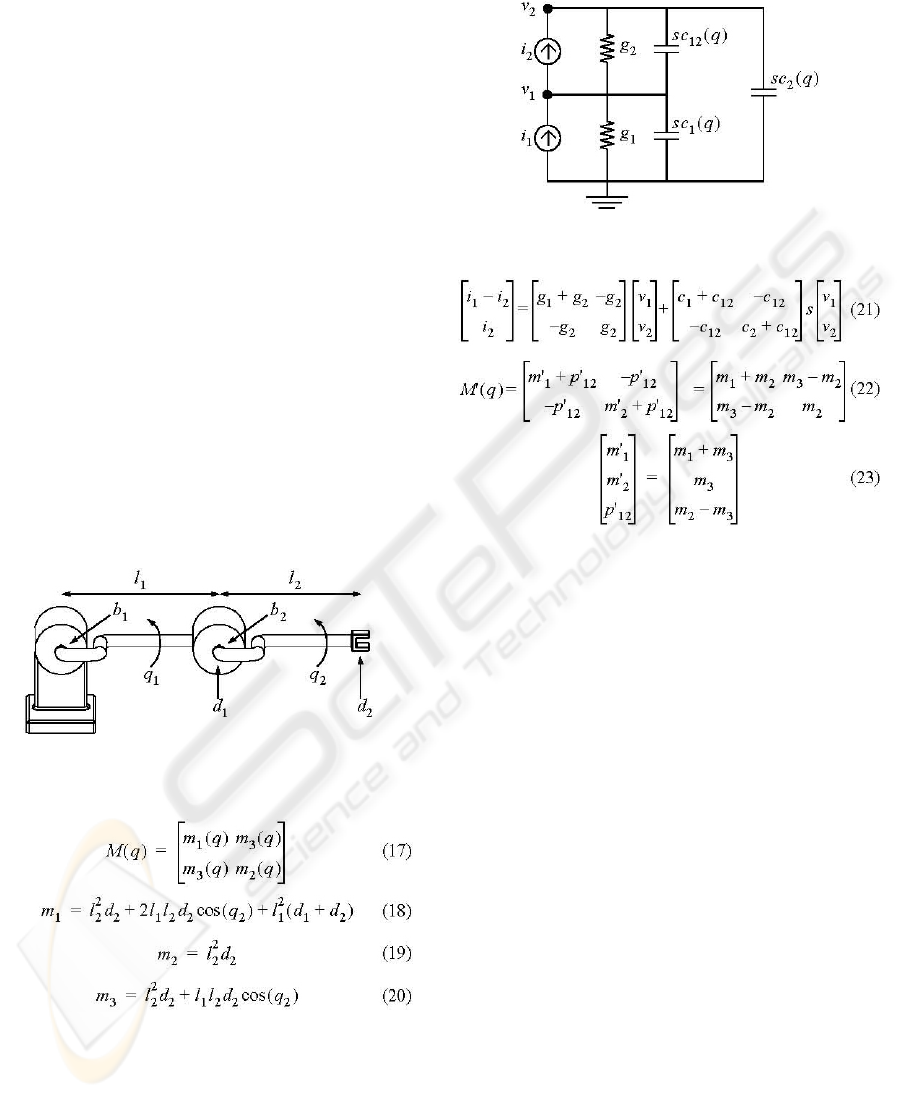
Consider the 2-DOF serial robot shown in Figure 10.

The mass matrix for this mechanism is approximated

in (Craig, 1989) by two point masses d

and d

placed

at the distal actuator and end-effector as indicated

below. The resulting mass matrix (17) has the terms

shown in (18-20) where q

and q

are the joint angles

and l

are the link lengths. Just as in the

previous example, actuator damping coefficients b

and b

are taken to dominate the total system

damping.

Figure 10: 2-DOF serial robot.

The equivalent circuit model of this system is

shown in Figure 11. It is similar to Figure 9 except

that the capacitor values are configuration dependent

and a third capacitor c

is included to model the

coupled mass terms that are present. Performing

nodal analysis results in (21) and the corresponding

M' matrix in (22) which can be rearranged to solve

for the mechanical model parameters in terms of the

physical mass values in (23).

B' is the same diagonal

matrix as in (14).

Figure 11: Electrical model of 2-DOF serial robot.

Note from (22) that

M' is diagonal (i.e. p'

=0)

when

=0. From (19,20), this is merely the special

case when q

= ±π⁄2. Therefore, it is not possible to

model this system using only masses due to their

implicit ground reference, as described in Section

2.1. The off-diagonal terms can, however, be

modelled using the MP model proposed in Section

2.2. It results in a mechanical system model that is

topologically identical to the equivalent circuit in

Figure 11 where each grounded capacitor (c

) is

replaced by a regular mass and each ungrounded

capacitor (c

) is replaced by an MP model since the

MP model is able to accommodate a non-zero

reference acceleration. The resulting mechanical

system is shown in Figure 12.

Although

has a negative value when –π⁄2<q

<π⁄2,

the net mass perceived by each actuator is always

positive because M is positive definite. When

negative, it simply means that the motion of actuator

1 reduces the net mass perceived by actuator 2, but

the net mass perceived by actuator 2 is always

greater than zero.

3.2 Parallel 2-DOF Robot

The same technique can be applied to parallel

manipulators such as the 2-DOF 5-bar linkage used

MECHANICAL SYSTEM MODELLING OF ROBOT DYNAMICS USING A MASS/PULLEY MODEL

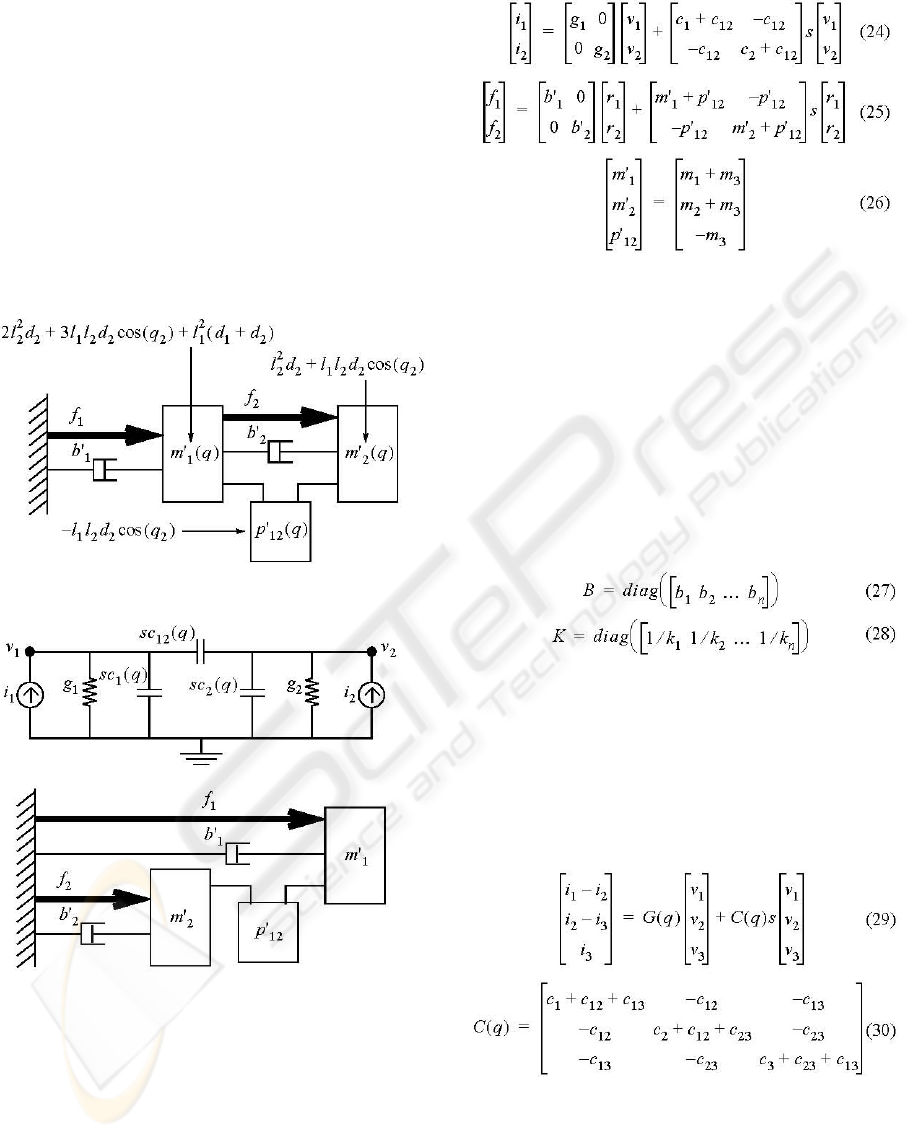
by (Hayward et al., 1994). In the case of parallel

manipulators, each actuator is referenced to ground

but there remains a coupling between the effective

mass perceived by each actuator which, like a serial

manipulator, is configuration dependent. This

coupling is modelled by c

and p'

in the equivalent

electrical and mechanical models shown in Figure

13. Typically, parallel manipulators also have

coupled damping terms due to their passive joints

which would be modelled by a conductance g

added between nodes 1 and 2 (i.e. in parallel with

). However, for the sake of simplicity, the

damping of the passive joints are neglected here.

Figure 12: Mechanical model of a 2-DOF serial robot.

Figure 13: Model of a 2-DOF parallel robot.

Performing nodal analysis on the circuit in

Figure 13 results in (24) by inspection. For a parallel

robot, currents and voltages correspond directly to

joint forces and joint rates so

B'= B and M'= M . For a

mass matrix of the form shown in (17), the elements

of the

M' matrix, and therefore the parameter values

associated with the masses and MP models of Figure

13, are shown in (26).

3.3 Multiple DOF Robots

This technique is easily extended to devices with

any number n of degrees of freedom. With serial

manipulators, the compliance and damping is often

mainly in the actuators and the damping B and

spring K matrices are diagonal (27,28). With parallel

manipulators, the B and K matrices typically contain

off-diagonal terms but they are easily modelled

using conventional techniques since springs and

dampers are 2-terminal devices which can be placed

at any two nodes in a system diagram.

To account for inertial cross-coupling, the

model must contain a capacitor and/or MP model

between every pair of actuators. For example, the

electric circuit model and corresponding mechanical

system model of a serial 3-DOF manipulator are

shown in Figure 14. The capacitance C matrix

resulting from the nodal analysis (29) of the circuit

in Figure 14 is shown in (30).

Just as in the previous examples, the 3x3 mass

matrix

M' (32) is rearranged into the form shown in

(31) to parallel the current/voltage relationship of

(29). For the mass matrix

M of the form shown in

(33), the entries of the

M' matrix are solved for in

(34).

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

Figure 14: Model of a 3-DOF serial robot.

Similarly, for a parallel 3-DOF robot, the electric

circuit model and corresponding mechanical system

model are shown in Figure 15. For a mass matrix of

the form shown in (33), the elements of

M' are

shown in (35).

Figure 15: Model of a 3-DOF parallel robot.

4 CONCLUSION

It is argued that a plain mass is not a complete and

general model of a capacitor since a mass only has

MECHANICAL SYSTEM MODELLING OF ROBOT DYNAMICS USING A MASS/PULLEY MODEL

one terminal whereas a capacitor has two. The

response of a mass corresponds to its acceleration

with respect to ground and, therefore, can only be

used to simulate a capacitor which has one terminal

connected to ground. It cannot be used to simulate a

capacitor which has a non-zero reference voltage. A

new model described here that consists of a mass

and a pulley correctly simulates the response of a

capacitor in the general case.

It is shown that the MP model can be used to

model systems with cross-coupled effective masses

which are otherwise, impossible to model with pure

masses alone. This includes both serial and parallel

manipulators with any number of degrees of

freedom. The mechanical system model that is

obtained fully describes the dynamic response of the

system and is topologically identical to its electric

circuit equivalent. As shown in (Stocco & Yedlin,

2006), this makes it possible to apply electric circuit

analysis techniques to mechanical systems, directly.

ACKNOWLEDGEMENTS

The authors gratefully acknowledge Tim Salcudean

for his valuable comments during the preparation of

this manuscript.

REFERENCES

Brune, O., 1931. "Synthesis of a finite two-terminal

network whose driving-point impedance is a

prescribed function of frequency". J. Math. Physics.

vol. 10, pp. 191-236.

Craig, J.J., 2005. “Introduction to Robotics Mechanics and

Control”. 3rd ed., Pearson Prentice Hall.

Eppinger, S., Seering, W., 1992. “Three Dynamic

Problems in Robot Force Control”. IEEE Trans.

Robotics & Auto., V. 8, No. 6, pp. 751-758.

Fairlie-Clarke, A.C., 1999. “Force as a Flow Variable”.

Proc. Instn. Mech. Engrs., V. 213, Part I, pp. 77-81.

Foster, R. M., 1924. "A reactance theorem". Bell System

Tech. J., vol. 3, pp. 259-267.

Hamill, D.C., 1993. "Lumped Equivalent Circuits of

Magnetic Components: The Gyrator-Capacitor

Approach". IEEE Transactions on Power Electronics,

vol. 8, pp. 97.

Hayward, V., Choksi, J., Lanvin, G., Ramstein, C., 1994.

“Design and Multi-Objective Optimization of a

Linkage for a Haptic Interface”. Proc. of ARK ‘94, 4th

Int. Workshop on Advances in Robot Kinematics

(Ljubliana, Slovenia), pp. 352-359.

Paynter, H.M., 1961. Analysis and Design of Engineering

Systems. MIT Press.

Sass, L., McPhee, J., Schmitke, C., Fisette, P., Grenier, D.,

2004. "A Comparison of Different Methods for

Modelling Electromechanical Multibody Systems".

Multibody System Dynamics, vol. 12, pp. 209-250.

Stocco, L., Yedlin, M., Sept. 2006. “Closing the Loop on

the Electro-Mechanical System Analogy”. Submitted

to: IEEE J. Circuits & Systems.

Tilmans, H.A.C., 1996. "Equivalent circuit representation

of electromechanical transducers: I. Lumped-

parameter systems". J. Micromech. Microeng, vol. 6,

pp. 157-176.

van Amerongen, J., Breedveld, P., 2003. "Modelling of

physical systems for the design and control of

mechatronic systems". Annual Reviews in Control,

vol. 27, pp. 87-117.

Yamakita, M., Shibasato, H., Furuta, K., 1992. “Tele-

Virtual Reality of Dynamic Mechanical Model”. Proc.

IEEE/RSJ Int. Conf. Intelligent Robots & Systems,

(Raleigh, NC), pp. 1103,-1110.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics