ADDRESSING COMPLEXITY ISSUES IN A REAL-TIME PARTICLE

FILTER FOR ROBOT LOCALIZATION

Dario Lodi Rizzini, Francesco Monica, Stefano Caselli

Dipartimento di Ingegneria dell’Informazione, Universit

a di Parma

Viale G. P. Usberti, 181/A, 43100 Parma, Italy

Monica Reggiani

Dipartimento di Informatica, Universit

a di Verona

Ca’ Vignal 2, Strada Le Grazie 15, 37134 Verona, Italy

Keywords:

Robot Localization, Real-Time, Particle Filters.

Abstract:

Exploiting a particle ﬁlter for robot localization requires expensive ﬁlter computations to be performed at

the rate of incoming sensor data. These high computational requirements prevent exploitation of advanced

localization techniques in many robot navigation settings. The Real-Time Particle Filter (RTPF) provides a

tradeoff between sensor management and ﬁlter performance by adopting a mixture representation for the set

of samples. In this paper, we propose two main improvements in the design of a RTPF for robot localization.

First, we describe a novel solution for computing mixture parameters relying on the notion of effective sample

size. Second, we illustrate a library for RTPF design based on generic programming and providing both

ﬂexibility in the customization of RTPF modules and efﬁciency in ﬁlter computation. In the paper, we also

report results comparing the localization performance of the proposed extension and of the original RTPF

algorithm.

1 INTRODUCTION

Robot localization is the problem of estimating robot

coordinates with respect to an external reference

frame. In the common formulation of the localization

problem, the robot is given a map of its environment,

and to localize itself relative to this map it needs to

consult its sensor data. A particularly effective ap-

proach to solve this problem is the probabilistic one,

due to the uncertainty affecting sensor data and move-

ment execution. For this reason, bayesian ﬁltering has

become the prevailing paradigm in recent works on

localization (Elinas and Little, 2005; Sridharan et al.,

2005).

A stochastic estimator provides a result expressed

in the form of a probability density function (PDF)

represented like a continuous function by Gaussian

ﬁlters (Kalman Filter, EKF) (Leonard and Durrant-

Whyte, 1991; Arras et al., 2002) or a discrete decom-

position of the state posterior by nonparametric ﬁl-

ters. The main nonparametric algorithm is called Par-

ticle Filter (Fox et al., 1999) and relies on importance

sampling (Doucet et al., 2001). With importance sam-

pling, the probability density of the robot pose is ap-

proximated by a set of samples drawn from a proposal

distribution, and an importance weight measures the

distance of each sample from the correct estimation.

The nonparametric approach has the advantage

of providing a better approximation of the posterior

when a parametric model does not exist or changes

during iteration, e.g. in initialization or when environ-

ment symmetries determine a multi-modal PDF. Even

if techniques like Multi-Hypothesis Tracking (Arras

et al., 2002) attempt to manage multi-modal distribu-

tions, particle ﬁlters are more efﬁcient and can rep-

resent all kinds of PDFs, including uniform distribu-

tions. Moreover, particle ﬁlters avoid linearizations

that can lead to poor performance and divergence of

the ﬁlter for highly nonlinear problems.

Unfortunately, particle ﬁlters suffer from compu-

tational complexity due to the large number of dis-

crete samples of the posterior: for each sample a

pose update, a correction and a resample step are per-

formed. Since localization can be performed slowly

with respect to the usual movement and tasks of the

robot, it would be conceivable to perform localiza-

355

Lodi Rizzini D., Monica F., Caselli S. and Reggiani M. (2007).

ADDRESSING COMPLEXITY ISSUES IN A REAL-TIME PARTICLE FILTER FOR ROBOT LOCALIZATION.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 355-362

DOI: 10.5220/0001617503550362

 SciTePress

tion over a large time interval. Therefore, there have

been attempts to adapt the number of samples (Fox,

2003). However, during an excessive time interval un-

certainty increases and many useful observations are

dropped; a proper interval to complete a particle ﬁlter

iteration should be approximately equal to the rate of

incoming data. A trade-off must therefore be reached

between time constraints imposed by the need of col-

lecting sensor data incoming with a given rate and the

number of samples determining localization perfor-

mance.

The Real-Time Particle Filter (RTPF) (Kwok

et al., 2004) is a variant of a standard particle ﬁlter

addressing this problem. This algorithm relies on the

decomposition of the posterior by partitioning the set

of samples in smaller subsets computed taking into

account the sensor data received in different time in-

tervals. By choosing the proper size for partitions, a

particle ﬁlter iteration can be performed aligned with

the sensor acquisition cycle.

While RTPF represents a remarkable step toward

a viable particle ﬁlter-based localizer, there are a few

issues to be addressed in developing an effective im-

plementation. RTPF convergence is prone to some

numerical instability in the computation of important

parameters of the algorithm, namely the coefﬁcients

of the mixture constituting the posterior. Further-

more, even adopting RTPF as the basic architecture,

the design of a ﬂexible and customizable particle ﬁl-

ter remains a challenging task. For example, life cy-

cle of samples extends beyond a single iteration and

covers an estimation windows in which mixture pos-

terior computation is completed. This extended life

cycle of samples impacts over software design. More-

over, RTPF addresses observations management and

derived constraints. A good implementation should

be adaptable to a variety of sensors.

This paper proposes improvements in both the al-

gorithmic solution and the implementation of RTPF.

In section 2, a novel approach in the computation

of mixture weights based on the effective number of

samples is proposed. This approach simpliﬁes RTPF

and tries to avoid spurious numeric convergence of

gradient descent methods. In section 3, a localiza-

tion library implementing a highly conﬁgurable par-

ticle ﬁlter localizer is described. The library takes

care of efﬁcient life cycle of samples and control data,

which is different in RTPF and standard particle ﬁl-

ter, and supports multiple motion and sensor mod-

els. This ﬂexibility is achieved by applying generic

programming techniques and a policy pattern. More-

over, differing from other particle ﬁlter implementa-

tions (e.g., CARMEN (Montemerlo et al., 2003)), the

library is independent from speciﬁc control frame-

works and toolkits. In section 4, simulation and ex-

perimental results are reported and compared with the

original RTPF performance. These results conﬁrm the

effectiveness and viability of the proposed algorithm

and its implementation.

2 ADDRESSING ALGORITHMIC

COMPLEXITY

In particle ﬁlters, updating the particles used to rep-

resent the probability density function (potentially a

large number) usually requires a time which is a mul-

tiple of the cycle of sensor information arrival. For ex-

ample, range scanners return hundreds of values per

scan, at a rate of several scans per second; vision sen-

sors often require advanced algorithms to identify vi-

sual landmarks (Se et al., 2002; Sridharan et al., 2005)

draining computational resources from the process of

localization.

Naive approaches, yet often adopted, include dis-

carding observations arriving during the update of the

sample set, aggregating multiple observations into a

single one, and halting the generation of new samples

upon a new observation arrival (Kwok et al., 2004).

These approaches can affect ﬁlter convergence, as ei-

ther they loose valuable sensor information, or they

result in inefﬁcient choices in algorithm parameters.

An advanced approach dealing with such situa-

tions is the Real-Time Particle Filters (RTPF), pro-

posed in (Kwok et al., 2004), which will be brieﬂy

described in the following.

2.1 Real-time Particle Filter

Assume that the system received k observations

within an estimation window, i.e. the time required

to update the particles. The key idea of the Real-Time

Particle Filter is to distribute the samples in sets, each

one associated with one of the k observations. The

distribution representing the system state within an

estimation window will be deﬁned as a mixture of the

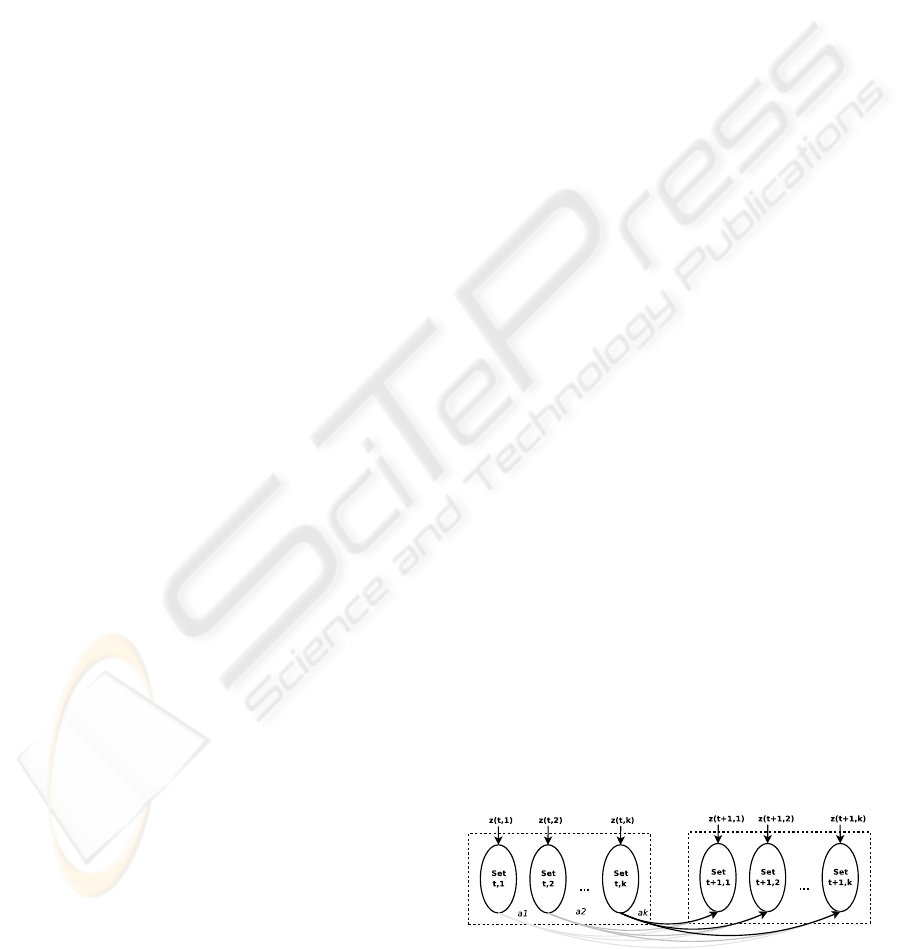
k sample sets as shown in Figure 1. At the end of each

Figure 1: RTPF operation: samples are distributed in sets,

associated with the observations. The distribution is a mix-

ture of the sample sets based on weights α

(shown as a

ﬁgure).

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

356

estimation window, the weights of the mixture belief

are determined by RTPF based on the associated ob-

servations in order to minimize the approximation er-

ror relative to the optimal ﬁlter process. The optimal

belief could be obtained with enough computational

resource by computing the whole set of samples for

each observation. Formally:

Bel

opt

) ∝

. . .

∏

i=1

p(z

) · p(x

i−1

, u

i−1

)

·Bel(x

)dx

···dx

k−1

(1)

where Bel(x

) is the belief generated in the previous

estimation window, and z

, u

, x

are, respectively,

the observation, the control information, and the state

for the i−th interval.

Within the RTPF framework, the belief for the i−

th set can be expressed, similarly, as:

Bel

) ∝

. . . p(z

) ·

∏

j=1

p(x

j−1

, u

j−1

) · Bel(x

)dx

. . . dx

k−1

(2)

containing only observation-free trajectories, since

the only feedback is based on the observation z

, sen-

sor data available at time t

The weighted sum of the k believes belonging to

an estimation windows results in an approximation of

the optimal belief:

Bel

mix

|α) ∝

∑

i=1

Bel

) (3)

An open problem is how to deﬁne the opti-

mal mixture weights minimizing the difference be-

tween the Bel

opt

) and Bel

mix

|α). In (Kwok

et al., 2004), the authors propose to minimize

their Kullback-Leibler distance (KLD). This mea-

sure of the difference between probability distribu-

tions is largely used in information theory (Cover and

Thomas, 1991) and can be expressed as:

J(α) =

Bel

mix

|α)log

Bel

mix

|α)

Bel

opt

)

(4)

To optimize the weights of mixture approxima-

tion, a gradient descent method is proposed in (Kwok

et al., 2004). Since gradient computation is not pos-

sible without knowing the optimal belief, which re-

quires the integration of all observations, the gradient

is obtained by Monte Carlo approximation: believes

Bel

share the same trajectories over the estimation

windows, so we can use the weights to evaluate both

Bel

(each weight corresponds to an observation) and

Bel

opt

(the weight of a trajectory is the product of the

weights associated to this trajectory in each partition).

Hence, the gradient is given by the following formula:

∂J

∂α

≃ 1+ Bel

log

∑

i=1

Bel

opt

(5)

where Bel

is substituted by the sum of the weights

of partition set i − th and Bel

opt

by the sum of the

weights of each trajectory.

Unfortunately, (5) suffers from a bias problem,

which (Kwok et al., 2004) solve by clustering samples

and computing separately the contribution of each

cluster to the gradient (5). In the next section, an al-

ternative solution is proposed.

2.2 Alternative Computation of Mixture

Weights

This section proposes an alternative criterion to com-

pute the values of the weights for the mixture belief.

Instead of trying to reduce the Kullback-Leibler di-

vergence, our approach focuses on evaluating the be-

lieves by synthetic values depending on the sample

weights of each partition. The concrete approxima-

tion given by (Kwok et al., 2004) for the gradient of

KL-divergence is a function of weights.

Real-time particle ﬁlter prior distribution is the re-

sult of two main steps: resampling of samples and

propagation of trajectories along the estimation win-

dow. The effect of resampling is the concentration of

previous estimation window samples in a unique dis-

tribution carrying information from each observation.

Conversely, the trajectories update given by odometry

and observation spreads the particles on partition sets.

Our attempt is to build synthetic values for each

element of the resampled distribution and of the par-

tition trajectory; this could be done using weights. Let

be the weight of the i −th sample (or trajectory)

of the j − th partition set. Then the weight partition

matrix is given by

W =





... w

... ...

... w





(6)

The weights on a row of this matrix trace the history

of a trajectory on the estimation window; a group of

values along a column depicts a partition handling

sensor data in a given time. Resampling and trajec-

tory propagation steps can be shaped using matrix W

and mixture weights α.

• Resampling. The effect of resampling is the con-

centration of each trajectory in a unique sample

whose weight is the weighted mean of the weights

ADDRESSING COMPLEXITY ISSUES IN A REAL-TIME PARTICLE FILTER FOR ROBOT LOCALIZATION

357

of the trajectory. In formula, the vector of trajec-

tory weights is given by t = W · α.

• Propagation. Projecting a sample along a trajec-

tory is equivalent to the computation of the weight

of the sample (i.e., the posterior) for each set given

the proper sensor information. Again, matrix W

gives an estimation of the weight. Trajectories

projection can thus be done with a simple matrix

product

α = W

·t = W

W · α (7)

Vector

α is a measure of the relative amount of

importance of each partition set after resampling

and propagation depending on the choice of coef-

ﬁcient α. Hence,

α is the new coefﬁcient vector

for the new mixture of believes.

Some remarks can be made about the matrix V =

W in (7). First, since we assume w

> 0, V is

a symmetric and positive deﬁnite matrix. Moreover,

each element j on the main diagonal is the inverse of

the effective sample size (see (Liu, 1996)) of set j

ef f

∑

i=1

(8)

The effective sample size is a measure of the efﬁ-

ciency of the importance sampling on each of the par-

tition sets. Therefore, the off-diagonal elements of V

correspond to a sort of importance covariances among

two partition sets. Thus we will refer to this matrix as

weights matrix.

Hence, a criterion to compute the mixture weights

consists of achieving a balance in the mixture forcing

α in (7) to be equal to α except for scale. The vector

is thus obtained by searching an eigenvector of matrix

V α = λ I α (9)

The eigenvector can be computed using the power

method or the inverse power method. This criterion

can be interpreted as an effort to balance the effective

number of samples keeping the proportion among dif-

ferent partition sets.

3 ADDRESSING SOFTWARE

COMPLEXITY

While the choice of the algorithm is a key step, in-

tegration of a localization subsystem in a real mobile

robot requires a number of practical issues and trade-

offs to be addressed. Real-time execution is the re-

sult of different aspects like communication and inte-

gration of the localizer with the robot control archi-

tecture, careful analysis in object creation/destruction

cycles, and tradeoffs between abstraction level man-

agement and efﬁciency.

This section describes a library designed to ef-

ﬁciently support the implementation of particle ﬁl-

ter localization algorithms, and speciﬁcally of RTPF.

The library aims at providing an efﬁcient yet open in-

frastructure allowing users to take advantage of the

provided genericity to integrate their own algorithms.

The library has been designed to be easily exploited

in different control systems for autonomous mobile

robots. In a functional layer, or controller, with the ba-

sic computational threads for robot action and percep-

tion, the localization task can be simply conﬁgured as

a computational demanding, low priority thread.

3.1 Design of the Library

Advanced localization algorithms like RTPF address

restrictions on real-time execution of localization due

to limited computational resources. However, strictly

speaking, real-time execution relies on the scheduling

and communication capabilities of the robot control

system which hosts the localizer. A localization sub-

system should therefore be properly integrated in the

control architecture. Nonetheless, localizer indepen-

dence from the underlying low level control layer is

a highly desirable property for a localization library.

The adaptable aspects of the localization library are

the data format and the models of the information pro-

vided by the physical devices of a mobile robots.

The functional analysis of the localization prob-

lem led to the identiﬁcation of four main components:

the localizer, the dynamic model of the system, the

sensor data model, and the map. Each of these com-

ponents is implemented by a class, which provides a

general interface to handle prediction, correction and

resampling phases of particle ﬁlters. However, there

are different ways of modelling details like sensor and

motion uncertainty, data formats of system state, con-

trol commands and observations, or implementation-

speciﬁc like map storage and access. In our library,

classes

Localizer

SystemModel

SensorModel

and

LocalizeMap

consist of a general interface which can

be adapted.

The strategy pattern (Gamma et al., 1995) is

the well-known design solution for decoupling algo-

rithms from system architecture: with this pattern, al-

gorithms can be modiﬁed and integrated in the appli-

cation without modifying the internal code. Thus, us-

ing external abstract strategy classes for each change-

able aspect of the localization subsystem, adaptation

to the robotic platform hosting the localizer can be

obtained. While this implementation avoids the hard-

wiring of user’s choices inside the localizer code, it

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

358

causes inefﬁciency due to the abstraction levels intro-

duced to support the polymorphic behavior. Further-

more, the strategy pattern cannot handle changes of

data types lacking an abstract base class; i.e., obser-

vation or control command types given by a generic

robot control architecture cannot be used directly.

These remarks, together with the observation that

choices are immutable at runtime, suggested the use

of static polymorphism. In the current library imple-

mentation, static polymorphism is effectively guaran-

teed by a generic programming approach, and in par-

ticular with policy and policy classes (Alexandrescu,

2001). This programming technique supports devel-

oper’s choices at compile time, together with type

checking and code optimization, by using templates.

template< S t a t e ,

SensorData ,

Control ,

SampleCounter ,

SampleManager ,

Fusion >

cl as s Lo cal ize r : public SampleManager<State>

{

Fusion<SensorData> fu s io n

;

public :

template< . . . > / / S t ateC o nver t er

Lo cal i ze r ( Pdf &pdf ,

State C onverter <...> &co nve r te r ) ;

˜ L oca liz e r ( ) ;

template< . . . > / / SystemModel Params

void update ( C o n t r o l &u ,

SystemModel <...> &sys ) ;

template< . . . > / / SensorModel Params

void update ( SensorData &z ,

SensorModel <...> &sen ) ;

} ;

Listing 1: The

Localizer

class.

The main component of the library, the class

Localizer

, exempliﬁes how policies allow man-

agement of different aspects of localization prob-

lem. Listing 1 shows a simpliﬁed interface of

the

Localizer

class, including only two

update()

methods. Note the template parameters of the class:

there are both data types (

State

SensorData

and

Control

) and policies related to particle ﬁlter execu-

tion. Methods

update()

allow the execution of pre-

diction and correction phases by using generic sensor

and motion models,

SensorModel

and

SystemModel

which are fully customizable interface classes with

their own polices too.

Policies in

Localizer

provide the required ﬂexi-

bility in RTPF implementation. The library supports

different versions of particle ﬁlters, and template pa-

rameters determine the actual algorithm implemented

in the system.

SampleCounter

allows choosing the

number of samples, that can be ﬁxed or adaptable,

e.g. with KL-distance (Fox, 2003).

SampleManager

is the class implementing sample management and

creation/destruction of data involved in computation.

This class plays an important role, since RTPF deter-

mines a complex life cycle for particles, as shown in

ﬁgure 2. While in standard particle ﬁlters samples and

control commands survive only during a single itera-

tion (prediction, correction, resampling), RTPF needs

the storage of data over the period of an estimation

window.

4 RESULTS

In this section, we describe RTPF performance eval-

uation both in a simulated environment and using ex-

perimental data collected by navigating a robot in

a known environment. One of the purposes of this

evaluation is the comparison of the two RTPF ver-

sions differing in their method for computing mixture

weights: the original method based on steepest de-

scent and the method described in this paper and rely-

ing on the eigenvalues of the weights matrix. Simula-

tions allow comparison of the two methods in a fully-

controlled environment, whereas experiments show

the actual effectiveness of the proposed technique.

4.1 Simulation

Several tests were performed in the simulated envi-

ronment shown in ﬁgure 3, which corresponds to the

main ground ﬂoor hallway in the Computer Engineer-

ing Department of the University of Parma. This

environment allows veriﬁcation of RTPF correctness

while coping with several symmetric features, which

may cause ambiguities in the choice of correct lo-

calization hypotheses. Real experiments with a mo-

bile robot were carried out in the same environment

and are described later in the paper: simulations have

helped with the setup of experiments and viceversa.

Two simulated paths exploited in simulation are also

shown in ﬁgure 3. These paths, labeled as Path 1 and

Path 2, correspond to lengths of approximately 7 m

and 5 m.

In simulation, the map is stored as a grid with a

given resolution (0.20 m) and is used both to create

simulated observations and to compute importance

weights in correction steps. Data provided to the lo-

calizer consist of a sequence of laser scans and mea-

surements: scanned ranges are obtained by ray trac-

ADDRESSING COMPLEXITY ISSUES IN A REAL-TIME PARTICLE FILTER FOR ROBOT LOCALIZATION

359

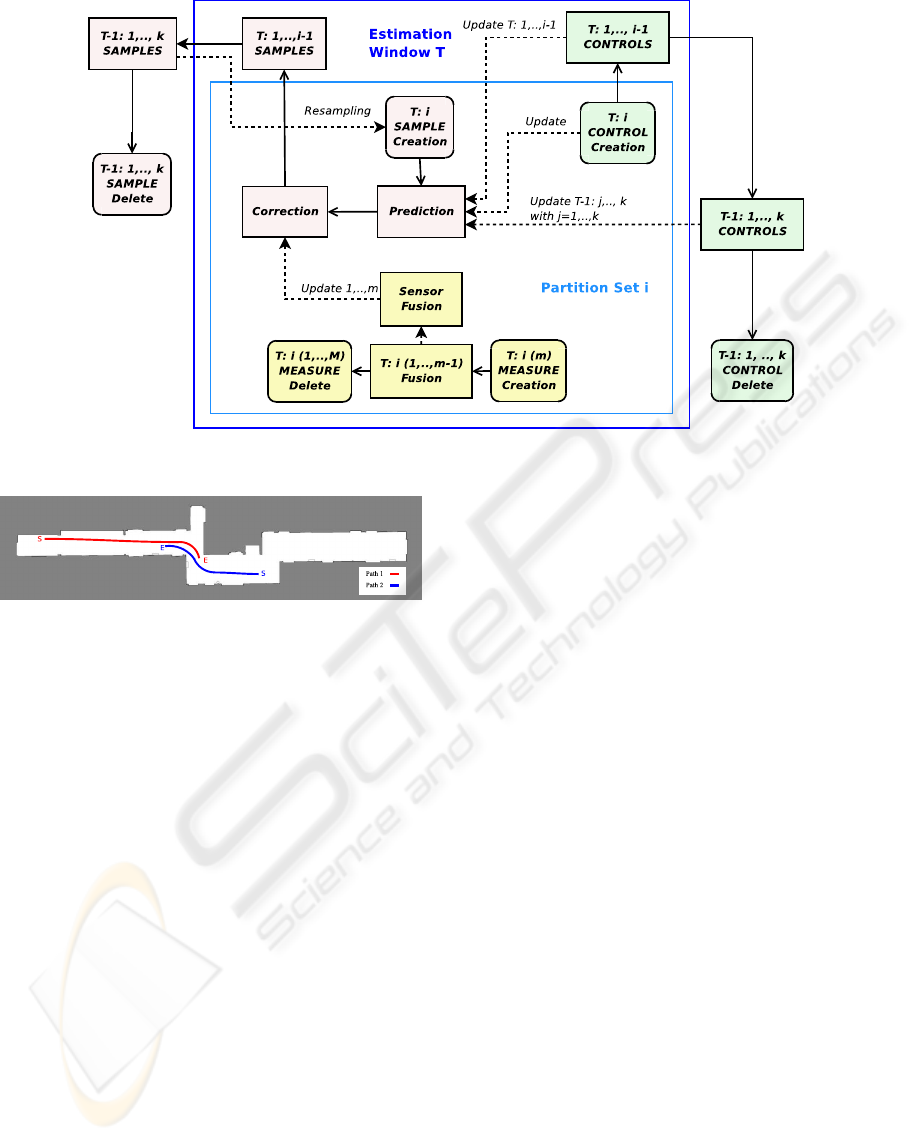
Figure 2: Life cycle for particle, measurement, and control objects within a single step in a real-time particle ﬁlter.

Figure 3: Hallway and simulated paths in the Computer

Engineering Department, University of Parma (S=Start,

E=End).

ing a beam on the discretized map. The measurement

model is also based on ray tracing and follows stan-

dard beam models for laser scanners (Thrun et al.,

2005). In our tests, we have used only three laser

beams measuring distances to left, right and frontal

obstacles; such poor sensor data stress the role of al-

gorithm instead of sensor data. A gaussian additive

noise is added to both range beams and robot move-

ments representing environment inputs and robot state

in simulation. The task of the robot is to achieve lo-

calization while moving in the map of ﬁgure 3 along

different trajectories.

Localization algorithms investigated are RTPFs in

the two versions: the original steepest descent-based

one (RTPF-Grad) and the proposed one based on the

effective number of samples (RTPF-Eig). During the

tests the partition set size is 1000 samples.

A summary of simulation results is reported in ﬁg-

ure 5. In the ﬁgure, curves show the localization error

for the two algorithms at each iteration by consider-

ing convergence to the nearest hypothesis. For both

curves, each value is obtained by averaging the dis-

tances of the estimated pose from the real pose over

10 trials where localization converged to the correct

hypothesis. For both algorithms there were also a few

simulation instances where localization did not con-

verge to the correct hypothesis within the length of

the path, although the correct hypothesis was the sec-

ond best. These unsuccessful cases, mostly occurring

on Path 2, were approximately 10% of all simulated

localization trials. We did not verify whether the robot

would recover its correct pose in the environment with

further navigation.

On the average, the two versions of the RTPF-

based localizer converged to some few hypotheses

after three iterations: the common samples distribu-

tion is multi-modal, as shown in ﬁgure 4 where there

are two local maxima. Hence, cluster search leads to

few hypotheses with different weight (an example is

shown in ﬁgure 4). In our tests a hypothesis close to

the correct robot pose always exists, and when this

hypothesis prevails there is a sudden change in lo-

calization error, as shown in ﬁgure 5. Convergence

is helped by recognizable features, e.g. the shape of

scans, but when the environment is symmetric it can

be difﬁcult to reach, especially with limited or noisy

sensoriality. Of course, the mean error trend in ﬁgure

5 does not correspond to any of the simulated trials;

rather, it is the result of averaging trials with quick

convergence and trials where the correct hypothesis

could only be recovered after many more iterations.

Figure 6 shows the percentage of simulation trials

converging to the correct hypothesis (i.e. with local-

ization error less than 1.5 m) at each iteration. Note

that for 40− 50% of simulation tests, convergence is

reached after few iterations. In other simulations, the

correct robot pose is recovered only after about 20 it-

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

360

Figure 4: A typical distribution of samples condensed around two prevailing hypotheses (crosses mark hypotheses, the circle

is centered in the robot position). When the wrong hypothesis has a higher weight, the localization error is huge.

0 5 10 15 20 25 30 35 40

Num. Iteration

Error [m]

RTPF−Grad

RTPF−Eig

Figure 5: Performance of the two RTPF versions in the sim-

ulated environment. The x-axis represents the iterations of

the algorithm. The y-axis shows the average error distance

of the estimated pose from robot pose.

0 5 10 15 20 25 30 35 40

100

Num. Iteration

% Test with error less than 1.5 m

RTPF−Grad

RTPF−Eig

Figure 6: Percentage of simulation trials converged to the

correct hypothesis, i.e. with localization error less than 1.5

m, during iterations for Map 1.

erations, i.e. after sensing map features that increase

the weight of the correct samples.

Empirically, for the examined environment RTPF-

Eig seems to exhibit a slightly faster convergence, on

the average, to the correct hypothesis, but its average

error after convergence appears somehow larger.

4.2 Experiments

Real experiments took place in the environment of

ﬁgure 3 collecting data with a Nomad 200 mobile

robot equipped with a Sick LMS 200 laser scanner.

The robot moved along Path 1 for about 5 m, from the

left end of the hallway in steps of about 15 − 20 cm

and reading three laser beams from each scan in the

same way of the simulation tests. In the real environ-

ment localization was always successful, i.e. it always

converged to the hypothesis closer to the actual pose

in less than 10 iterations (remarkably faster than in

simulation). Localization error after convergence was

measured below 50 cm, comparable or better than in

simulation.

To assess the consistency of the localizer’s output

on a larger set of experiments, we compared the robot

pose computed by the localizer (using the RTPF-Eig

algorithm) with the one provided by an independent

localization methodology. To this purpose, some vi-

sual landmarks were placed in the environment and on

the mobile robot, and a vision system exploiting the

ARToolKit framework (Kato and Billinghurst, 1999)

was exploited to triangualate the robot position based

on these landmarks. The vision system provided an

independent, coarse estimate of the robot pose at any

step, and hence allowed to establish convergence of

the RTPF-based localizer. The two localization esti-

mates were computed concurrently at each location

and stored by the robot.

Figure 7 shows the results of 10 tests of RTPF-

Eig over about 20 iterations. These results conﬁrm

that RTPF-Eig achieves localization to the correct hy-

pothesis very fast in most experiments. After conver-

gence, the maximum distance between RTPF-based

and vision based estimates is about 70 cm due to the

compound error of the two systems.

5 CONCLUSION

Localizing a mobile robot remains a difﬁcult task: al-

though effective algorithms like particle ﬁlters exist,

ADDRESSING COMPLEXITY ISSUES IN A REAL-TIME PARTICLE FILTER FOR ROBOT LOCALIZATION

361

0 5 10 15 20 25

Num. Iteration

Discrepancy Localizer−ARToolKit [m]

Figure 7: Discrepancy between RTPF-Eig and ARToolKit

estimations using real data collected in the hallway of Map

setting up a concrete localization system must deal

with several architectural and implementation prob-

lems. One of these problems is the tradeoff between

sensor data acquisition rate and computational load.

Solutions like RTPF have been proposed to achieve

this tradeoff, and are open to a number of improve-

ments. Therefore, localization involves conﬁguring

customizable features both in the algorithm and in

modules for sensor data, motion models, maps and

other algorithmic details. A good generic implemen-

tation should provide components that the end user

can adapt to his needs.

This paper has presented some improvements of

the RTPF algorithm. In the proposed enhancement,

the weight mixture of sample sets representing the

posterior are computed so as to maximize the effec-

tive number of samples.

A novel RTPF implementation based on the en-

hanced algorithm has been developed. Experiments

reported in the paper have shown this implementation

to work both in simulated environments and in the real

world. Assessing its relative merit with respect to the

original RTPF proposal requires further investigation.

ACKNOWLEDGEMENTS

This work was supported by ”LARER – Laboratorio

di Automazione della Regione Emilia-Romagna.” We

thank Bruno Ferrarini for his help with the experimen-

tal assessment.

REFERENCES

Alexandrescu, A. (2001). Modern C++ Design: Generic

Programming and Design Pattern Applied. Addison-

Wesley.

Arras, K. O., Castellanos, H. F., and Siegwart, R.

(2002). Feature-based multi-hypothesis localization

and tracking for mobile robots using geometric con-

straints. IEEE Int. Conf. on Robotics and Automation,

2:1371–1377.

Cover, T. M. and Thomas, J. A. (1991). Elements of Infor-

mation Theory. Wiley.

Doucet, A., de Freitas, J., and Gordon, N. (2001). Sequen-

tial Monte Carlo Methods in Practice. Springer.

Elinas, P. and Little, J. (2005). σMCL: Monte-carlo local-

ization for mobile robots with stereo vision. Proc. of

Robotics: Science and Systems.

Fox, D. (2003). Adapting the sample size in particle ﬁlters

through KLD-sampling. Int. J. of Robotics Research,

22(12):985–1003.

Fox, D., Burgard, W., and Thrun, S. (1999). Monte Carlo

Localization: Efﬁcient position estimation for mobile

robots. Proc. of the National Conference on Artiﬁcial

Intelligence.

Gamma, E., Helm, R., Johnson, R., and Vlissides, J. (1995).

Design Patterns: elements of reusable object-oriented

software. Addison-Wesley.

Kato, H. and Billinghurst, M. (1999). Marker tracking and

hmd calibration for a video-based augmented reality

conferencing system. Proc. of the Int. Workshop on

Augmented Reality.

Kwok, C., Fox, D., and Meil

a, M. (2004). Real-time particle

ﬁlters. Proc. of the IEEE, 92(3):469–484.

Leonard, J. J. and Durrant-Whyte, H. F. (1991). Mobile

Robot Localization by Traking Geometric Beacons.

IEEE Int. Conf. on Robotics and Automation.

Liu, J. (1996). Metropolized independent sampling with

comparisons to rejection sampling and importance

sampling. Statistics and Computing, 6(2):113–119.

Montemerlo, M., Roy, N., and Thrun, S. (2003). Perspec-

tives on standardization in mobile robot programming:

The Carnegie Mellon navigation (CARMEN) toolkit.

IEEE/RSJ Int. Conf. on Intelligent Robots and Sys-

tems.

Se, S., Lowe, D., and Little, J. (2002). Mobile robot lo-

calization and mapping with uncertainty using scale-

invariant visual landmark. Int. J. of Robotics Re-

search, 21(8):735–758.

Sridharan, M., Kuhlmann, G., and Stone, P. (2005). Practi-

cal vision-based monte carlo localization on a legged

robot. IEEE Int. Conf. on Robotics and Automation,

pages 3366–3371.

Thrun, S., Burgard, W., and Fox, D. (2005). Probabibilistic

Robotics. MIT Press, Cambridge, MA.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

362