
A NEW LOAD ADJUSTMENT APPROACH FOR JOB-SHOPS
Z. Bahroun
LIP2, Faculté des Sciences de Tunis, Dép. des Sciences de l’Informatique, 2092 Manar II, Tunis, Tunisie
J.-P. Campagne
Laboratoire LIESP, INSA-LYON, F-69621 Villeurbanne Bat B. Pascal, 7 av J. Capelle, France
M. Moalla
LIP2, Faculté des Sciences de Tunis, Dép. des Sciences de l’Informatique, 2092 Manar II, Tunis, Tunisie
Keywords: Load adjustment, Finite capacity, overlapping production planning, margins management, job-shop.
Abstract: This paper presents a new load adjustment approach by overlapping for a set of jobs in a job-shop contex
t,
guaranteeing the existence of a limited capacity schedule without scheduling under the assumption of pre-
emptive tasks. This approach is based on the exploitation of the tasks scheduling time segments overlapping
and on the distribution of the job’s margins between tasks in a just in time context. First, we present a
literature review concerning load adjustment approaches. Second, we introduce the overlapping load
adjustment approach. Third, we present an original heuristic to use this approach in the case of job-shops
organized firms. After that, we present the scheduling approach. Finally, we will discuss a more general use
of this approach and the possible extensions.
1 INTRODUCTION
Generally, the production planning is made in a
hierarchical way in two planning and scheduling
decision levels. In the first step, we decide which
products to supply, in which quantities and delays,
in the second step, we adjust load to the capacity and
schedule the tasks on the machines.
There are three main and classical load
adj
ustment approaches. First of all, we have the
placement. This approach consists in calculating a
detailed tasks schedule. A new task is integrated in
the planning if we find a gap in the planning which
is bigger than the duration of this task. This
approach estimates only one schedule which can be
destructed by any disturbance. The second approach
is the periodic and cumulative approach. It consists
in calculating the cumulative load and capacity for a
latest loading and for each period. This approach
does not guarantee the existence of a scheduling
solution because it does not take into consideration
the ready dates constraints. The third approach is the
periodic and non cumulative approach. It consists in
assigning tasks to periods and comparing period by
period the available and the required capacities. This
method estimates only the solutions in which the
tasks are fixed in a specific period.
Some researchers studied the problem of
seq
uencing decisions in production planning and
scheduling. Dauzere-Peres and Laserre (1999) think
that it is better in some cases to integrate the
scheduling decision level in the lot sizing decision
level and propose an iterative approach for planning
and scheduling production. Some researchers
integrated the scheduling and capacity constraints in
their lot sizing model (see for example, Fleishmann
and Meyr, 1997). We can also find a survey on lot
sizing and scheduling in Drexl and Kimms (1997).
However, most of these approaches consider
generally a single machine and are difficultly
applicable for real and industrial context.
Many researchers studied also the problem of
finite
capacity planning. We can state very briefly H.
Hillion and Proth (1994) who studied the problem of
276
Bahroun Z., Campagne J. and Moalla M. (2007).
A NEW LOAD ADJUSTMENT APPROACH FOR JOB-SHOPS.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 276-283
Copyright
c
SciTePress
a finite capacity flow control in a multi-stage/multi-
product environment or Gunther (1987) who also
developed two heuristics for the lot sizing in the
context of finite capacity. Néron et al (2001)
developed an approach for solving hybrid flow shop
problem using energetic reasoning. This approach
has some similarities in the concept with our
approach. Indeed, the energetic reasoning was
developed to solve “cumulative scheduling
problems”. The approach aims to develop
satisfiability tests and time-bound adjustments to
ensure that a given schedule is not feasible or
derives some necessary conditions that any feasible
schedule must satisfy.
In comparison with all these approaches, the
overlapping load adjustment approach allows to
distinguish two main phases. The first phase consists
on establishing a long or mid term production
planning where the feasibility is ensured without
scheduling and tasks placement, which allows us to
characterize a set of feasible scheduling solutions.
The scheduling will be done only in the second
phase.
2 THE OVERLAPPING LOAD
ADJUSTMENT APPROACH
The time scale is divided into time periods. Each
task of a job has got a processing time, requires one
or more resources and has to be realized during a
scheduling time segment associated with one or
more consecutive periods. The scheduling time
segments of consecutive tasks of the same job
cannot overlap From now on and throughout this
paper a lapse of time called here lapse, designates a
succession of a number of n consecutive periods. Let
(a,b) be a lapse composed of a succession of periods
which are limited by the periods a and b including
them. The shortest lapses are composed of only one
period, for instance (a,a). Such a lapse (a,a) is called
a basic lapse. The longest lapse is noted (1,H) in
which number 1 is associated with the first period of
the planning time frame and the letter H the last one.
From such a planning time frame, the total number
of different lapses is equal to H*(H+1)/2.This
number is of course to be multiplied by the number
of existing processors. The sub-lapse of a lapse is a
subset of one or more consecutive periods of this
lapse. For instance, the sub-lapses of [1,3] are [1,1],
[2,2], [3,3], [1,2] and [2,3]. Every lapse containing a
lapse [a,b] is called the over-lapse of [a,b]. For
instance, [1,3] is an over-lapse of [1,1]. Each lapse is
characterized by:
- An accumulated capacity: sum of the capacities of
each period included in this lapse.
- A direct capacity requirement: sum of the
capacities required by the tasks whose scheduling
time segment is exactly equal to this lapse.
- An accumulated capacity requirement: sum of the
capacities required by the tasks whose scheduling
time segment is fully included in this lapse. It is the
sum of the direct capacity requirements of this
lapse and its sub-lapses.
Dillenseger (1993) sets the following proposition
out: for any lapse, its accumulated capacity
requirement must be equal or smaller than its
accumulated capacity. He proves that it is a
necessary and sufficient condition for the existence
of a loading solution of the set of tasks (within the
limits of their scheduling time segments and
considering the capacity levels), according to pre-
emptive possibility.
Let’s consider the following example of a
production plan composed of 7 jobs which will be
treated on a single processor with ready and due
dates as shown in Table 1 below. The considered
period for this example is the week composed of five
days (the day is the unit time):
Table 1: Example 1.
Job processing
time (days)
Ready date (beginning
of the week)
Due date (ending
of the week)
A 2 3 4
B 4 2 4
C 4 4 5
D 1 3 3
E 2 3 3
F 2 2 3
G 4 4 5
Periods
(
weeks
)
Week 1
A
(
2
)
G
(
4
)
C
(
4
)
D
(
1
)
E
(
2
)
F
(
2
)
B
(
4
)
Load in days
Scheduling time
se
g
ment
Week 2
Week 3 Week 4
Week 5
Day1 of week 2
22
33
44
55
23
34
45
24
35
25
0
0
5
3
3
2
0
0
5
0
0
5
5
2 5
5
2
5
8
8
2
11
4 4
13
0 2
19
0 1
A
ccumulated ca
p
acit
y
(
da
y
s
)
5
10 15 20
Legend:
23
5
2 5
Accumulated
capacity requirement
(days)
Lapse [2,3]
Direct capacity
requi rement
(days)
Remai n in g
capacit y
(days)
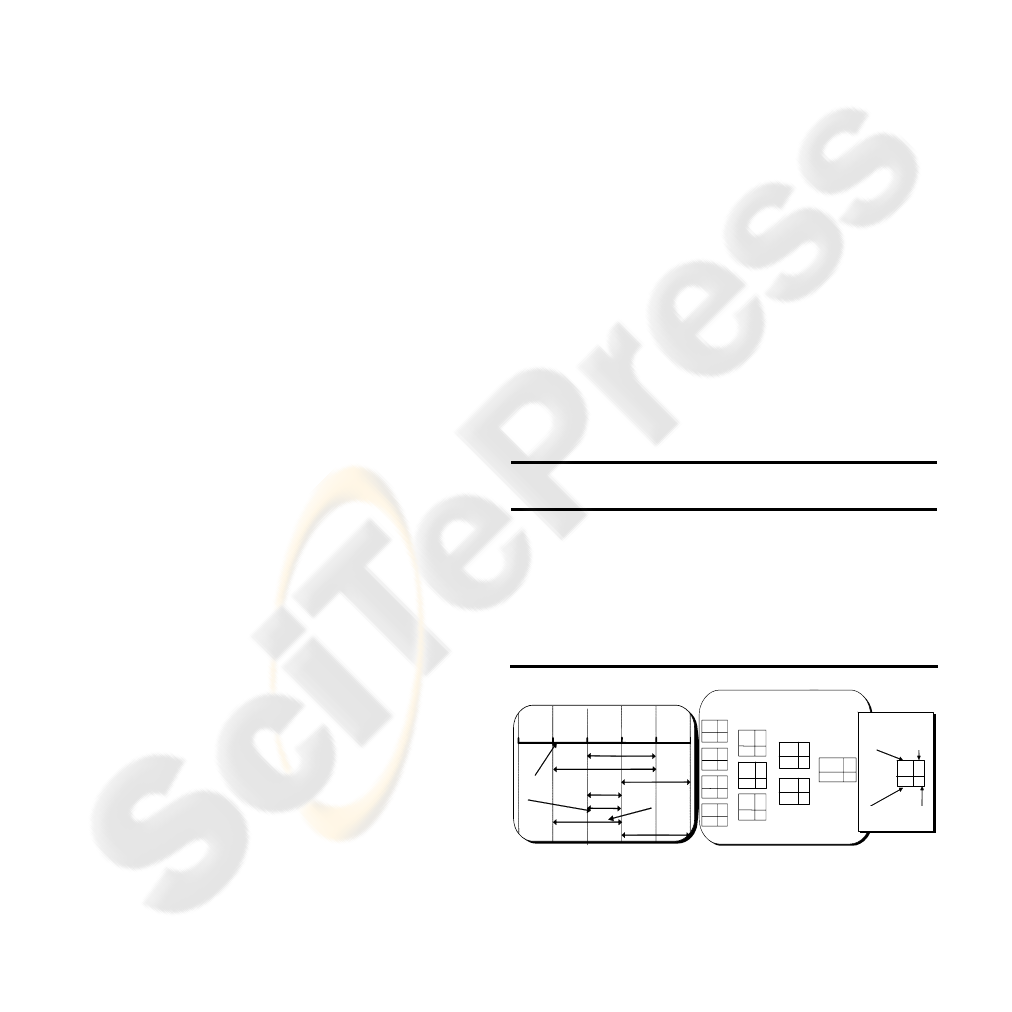
Figure 1: Capacity requirements planning (CRP) and
Planning feasibility control graph (PFCG).
Figure 1 represents a capacity requirement
planning (CRP) corresponding to the example of
Table 1. For instance, task G needs a load of 4 days
A NEW LOAD ADJUSTMENT APPROACH FOR JOB-SHOPS
277

(time units) and have a time scheduling segment
composed of weeks 4 and 5 (it means that this task
should be scheduled and produced in any time inside
the weeks 4 and 5). The capacity of a period is 5
days. The margin of task G is so equal to 6 days (10
days of weeks 4 and 5 minus its load of 4 days). The
associated planning feasibility control graph (PFCG)
is shown in Figure 1. For each lapse of weeks we
calculate the direct capacity requirement, the
accumulated capacity requirement and the remaining
capacity. For instance, the lapse [2, 3] composed of
weeks 2 and 3 has a direct capacity requirement
equal to 2 days (task F), an accumulated capacity
requirement equal to 5 days (tasks with a scheduling
time segment included in the lapse: D, E and F) and
a remaining capacity equal to (10-5) days. The
planning feasibility control graph proves the
feasibility of this set of jobs (all the remaining
capacities are positive).
Firstly, this load adjustment approach was
applied to plan the activities of a make-to-order
company in a mono-level context (Dillenseger,
1993). This approach was applied then to a flow-
shop composed of m processors (Bahroun, 2000a),
to a generalised flow-shop (Bahroun, 2000b) and for
the cyclic production context (Bahroun, 1999).
3 APPLICATION FOR JOB-SHOP
ORGANIZED FIRMS
Processor 1
Processor 3 Processor 4
Processor 4
Processor 2
Processor 1
Processor 2
Processor 1
Processor 4
Job 1:
Processor 1
Processor 3 Processor 4
Processor 2
Job 2:
Job 3:
Job 4:
Job 5:
Figure 2: Example of a job shop.
Let us consider N jobs with their due and ready
dates. Each job is composed of one to m tasks
realized on one to m processors with a certain order
which is not necessarily the same for all the jobs
(Figure 2).We suppose that these jobs are the results
of a products supply calculation in an M.R.P. based
system for instance. We aim at adjusting the load
resulted by these jobs in a finite capacity way by
adapting the overlapping load adjustment approach
to the job shop case.
We will first calculate the scheduling time
segment of each task, considering the due and the
ready dates of their job, their precedence constraint
and the capacity constraints. After that, we will try
to exploit the existing margins. They will be
distributed on the different job’s tasks and will be
assigned with priority to the tasks corresponding to
overloaded processors. We have developed a
heuristic which tries to share out judiciously the
job’s margins on their tasks. For this, we calculate a
latest loading on all the processors without margins
(we only assign the margins of jobs with a unique
task). We classify in the load decreasing order the
processors. We then assign all the margins to the
most loaded processor and after that we keep only
the necessary margins to validate the processor
loading (for any lapse, its accumulated capacity
requirement must be equal or smaller than its
accumulated capacity) and transfer the unused
margins to the next processor accordingly to the load
classification. Then, we reiterate the same treatment
to the next processor until reaching the last
processor.
We define the following parameters:
• N = number of jobs
• m = number of processors
• Ma
i
= the global margin of job i
• p
ij
= processing time of the task corresponding to
job i on processor j.
• p
ij
= 0 if there is not a task of job i on processor j.
• r
i
= release or ready date of job i
• d
i
= due date of job i
• b
ij
= beginning of the scheduling time segment of
the task corresponding to job i on processor j
• e
ij
= ending of the scheduling time segment of the
task corresponding to job i on processor j
• ACCP[a,b]
j
= accumulated capacity of the lapse
[a,b] for processor j
• ACCPR[a,b]
j
= accumulated capacity requirement
of the lapse [a,b] for processor j
• RC[a,b]
j
= remaining capacity of the lapse [a,b]
on processor j
• d
p
= duration of an elementary period.
We note ⎡x⎤ the smallest integer which is greater
than or equal to x and ⎣x⎦ the biggest integer which
is smaller than or equal to x.
Our approach is based on four main steps (we
will illustrate our approach with the example of
Table 2):
1
st
step :
We calculate the global job’s margins:
Ma
i
= d
i
- r
i
- (
j
m
=
∑
1
⎡(p / d )⎤ ) + 1
ij p
(1)
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
278
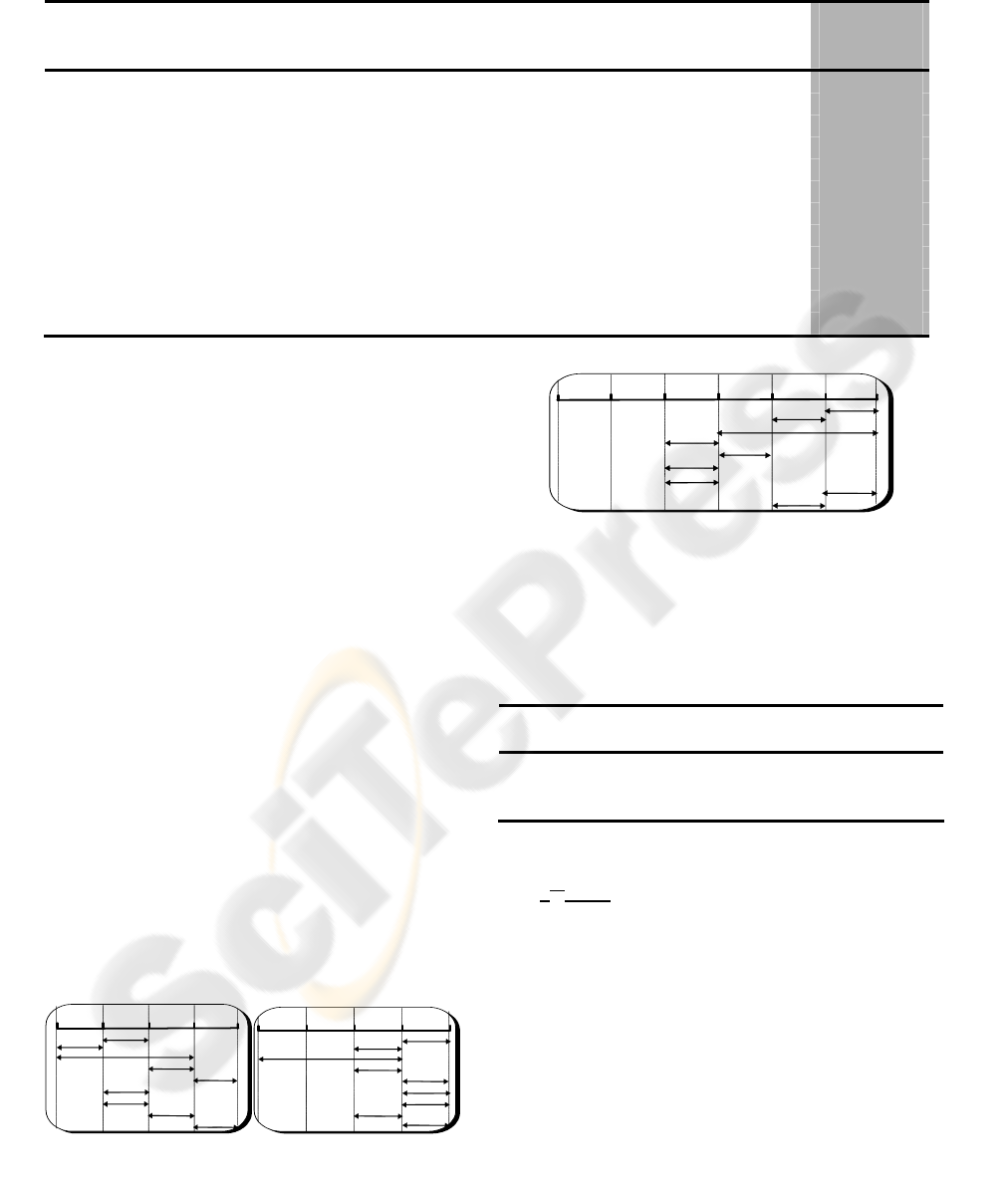
Table 2: Exemple 2.
Job Processing
order
Process. time
on proc. 1
(days)
Process. time
on proc.2
(days)
Process. Time
on proc. 3
(days)
ready date
(beginning of the
period)
due date
(ending of the
period)
Global margins
in periods
(weeks)
A P1→P2→P3 3 2 2 1 6 3
B P1→P2→P3 2 3 1 1 5 2
C P1 3 0 0 3 5
2
D P2 0 2 0 2 4 2
E P3 0 0 2 4 6
2
F P3→P2→P1 3 3 2 2 5
1
G P3→P2→P1 1 1 1 2 6 2
H P3→P1→P2 2 2 2 3 5
0
I P3→P1→P2 1 2 2 3 5
0
J P2→P1 3 3 0 2 5 2
K P2→P3 0 3 4 3 6
2
L P3→P1 2 0 3 4 6
1
For our example, we consider a production
system composed of three processors (P1, P2 and
P3) and a set of jobs (Table 1, d
p
= 5 days). We
calculate the global margins using the last formula
and we obtain the results reported in the last column
of Table 2. After that, we determine the scheduling
time segment of each task according to a latest
loading without margins (we assign only the margins
of jobs with a unique task like jobs C, D and E, in
fact, these margins will be used only on a unique
processor and will not be distributed on several
processors). For instance, for job A, the last task on
processor P3 will have a scheduling segment that
ends at the end of week 6 and will begin so, at the
beginning of the same week (because the processing
time of this task is inferior to a week), the task
number 2 for the same job A on processor P2 will
have a scheduling segment that begins and ends at
week 5. The first task of Job A on processor P1 will
have a scheduling segment that ends and begins at
week 4. Job C is composed of only one task, so we’ll
assign its margin and the time scheduling segment
will begin at week 3 and ends at week 5. We
calculate the scheduling segments of the other jobs
in the same way and we obtain the capacity
requirement planning of P1, P2 and P3 as shown in
Figures 3 and 4.
Periods
(
weeks
)
3 4 5
A1
(
3
)
F1
(
3
)
G1
(
1
)
H1
(
2
)
I1
(
1
)
J1
(
3
)
L1
(
2
)
6
B1
(
2
C1
(
3
)
Periods
(
weeks
)
2 3 4 5
A2
(
2
)
F2
(
3
)
G2
(
1
)
H2
(
2
)
I2
(
2
)
J2
(
3
)
K2
(
3
)
B2
(
3
)
D2
(
2
)
Figure 3: Capacity requirements planning (CRP) of P1
and P2 before treating.
Periods
(
weeks
)
12 34 5
A3
(
2
)
F3
(
2
)
G3
(
1
)
H3
(
2
)
I3
(
2
)
K3
(
4
)
L3
(
3
)
6
B3
(
1
)
E3
(
2
)
Figure 4: Capacity requirements planning (CRP) of P3
before treating.
After that, we calculate the total load and the
load by period for each processor as follow:
Table 3: Calculation of the processor load.
Proces. Total load in
days
Number of concerned
Periods(weeks)
Load/period
P1 20 4 5
P2 21 4 5,25
P3 19 4 4,75
We classify and treat the processor in the
decreasing order of the load/period: P2, P1, P3.
2
nd
step:
We assign all the global margins to the processor
P2. Then, we calculate for each task the beginning
and the ending periods of the scheduling time
segment of this task:
∀ i and for a processor j:
e
ij
remains the same
b
ij
= e
ji
- Ma
i
- ⎡(p
ij
/ d
p
)⎤ + 1
(2)
If we calculate the beginning time of the second
processor of our example, we can generate the
A NEW LOAD ADJUSTMENT APPROACH FOR JOB-SHOPS
279

corresponding capacity requirement planning (CRP)
and the planning feasibility control graph (PFGC):
Periods
(
weeks
)
2 3 4 5
A2
(
2
)
F2
(
3
)
G2
(
1
)
H2
(
2
)
I2
(
2
)
J2
(
3
)
K2
(
3
)
B2
(
3
)
D2
(
2
)
22
33
44
55
23
34
45
24
35
25
0
0
5
0
0
5
0
0
5
4
4
1
0
0 10
3
3
7
4
0
6
11
8 4
11
4 4
21
2 -1
Accumulated capacit y (days)
5
10 1
5
20
Legend:
24
11
8 4
Accumulat ed
capaci ty requi rement
Lapse [2,4]
Dir ect capaci ty
requi rement
Remaining
capaci ty
66
0
0
5
56
4
0
6
46
4
0 11
36
11
0 9
26
21
0
4
2
5
Figure 5: CRP and PFCG of the processor P2 after
assigning all the margins.
3
rd
Step:
We then check the feasibility condition. If we
find problems in certain lapses (even with all
available margins), we should lengthen the
scheduling time segment of some tasks. If for a lapse
[a,b] in the processor j, the validation condition is
not verified:
- We consider in the duration increasing order all
the tasks that b
ij
≥ a et e
ij
= b.
- In this list, we begin to treat the first task in the k
th
position in the list with a load equal or superior to
the overloading in the lapse which allows us to
delay the minimum number of tasks.
- We proceed progressively to the lengthening of
the scheduling time segment of these tasks, period
by period until the verification of the feasibility
condition or arrival to the end of the list.
- If we arrive to the end of the list we try with tasks
positioned in the (k-1)
th
, (k-2)
th
… position until
the verification of the feasibility condition.
In our example (Figure 5), we remark that we
have an overloading in the lapse [2,5] which obliges
us to delay of one period, one of the tasks included
in this lapse and which finishes in period 5 (A2, G2,
H2, I2 or K2 as we can see in CRP of Figure 5). We
choose in this example to lengthen the scheduling
time segment of task G2 from the lapse [3,5] to the
lapse [3,6].
Remark: If we do not accept to delay jobs, the
lapses with negative remaining capacity indicate
where we must increase the capacity by using for
example overtime or interims. We can also introduce
the notion of jobs priority for choosing which tasks
must be delayed.
4
th
Step:
Now, we will try to regain margins. We begin
with the tasks corresponding to jobs with weak
global margins. Tasks of jobs without margins are
assigned to the elementary lapses ([1,1], [2,2] etc.),
those corresponding to jobs with one period margin
are assigned to the lapses of the second column of
the feasibility control graph, those corresponding to
jobs with k periods margins are assigned to the
column number k etc. Our treatment begins with the
lapses of the second column because the
corresponding jobs have only one period global
margin and we must preserve these precious margins
to validate the other processors and use the margins
from jobs that have important global margins.
A transfer of a task from the lapse [a,b] to the
lapse [a+w,b], adds load to all the over-lapses of
[a+w,b] which are not initially over-lapses of [a,b].
The transferred load must be equal or smaller than
the remaining capacity on these lapses for
maintaining the validation condition.
The proposed approach for this transfer tries to
transfer the maximum number of tasks and tries to
match in the best way the transferred load in regard
to the remaining capacity. Consequently, we
construct the set of tasks which can be transferred,
and we classify this set in the increasing order of
their load. We transfer the tasks one by one in this
order while the sum of their load is smaller than the
remaining capacity. Then, we take the last task
transferred and we try to change it by another task
from the remaining tasks of the set and which
matches better the remaining capacity. If two tasks
have the same load we can choose for example the
task corresponding to a product with a greater
carrying cost. If we take the example of PFCG in
Figure 5, we begin with the lapses of the second
column. If we try, for instance, to regain margins
from the tasks corresponding to the lapse [3,4], we
should transfer the maximum number of tasks to the
lapse [4,4]. We can transfer task F2 because the
minimum of the remaining capacity of the over-
lapses of [4,4] which are not over-lapses of [3,4] (the
lapses [4,4], [4,5] and [4,6]) is 5 and it is greater
than the load of the task F2. Then, we pass to lapses
[4,5], [5,6], and next to the lapses of the third
column (for the task G2, we succeed to regain 2
periods, the scheduling time is shortened from the
lapse [3,6] to lapse [5,6]). We reiterate this treatment
until arriving to the last column. We obtain after
treatment of the processor P2 the capacity
requirement planning of Figure 6.
Periods
(
weeks
)
12 34 5
A2
(
2
)
F2
(
3
)
G2
(
1
H2
(
2
I2
(
2
)
J2
(
3
)
K2
(
3
6
B2
(
3
)
D2
(
2
)
Figure 6: C.R.P. of processor P2 after treatment.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
280

We can generalize this step for a processor j:
∀ the lapse [x,y] / x= a and y= a+w with 1 ≤ w ≤ H
and 1 ≤ a ≤ H-w :
- Construct the set A = {set of tasks / b
ij
= a and e
ij
= a+ w} (The set of tasks that their scheduling time
segment can be shortened, this set will be ordered
in the increasing order of their load).
- Iterate then for f = w -1 → 0
¾ Cap = Min ( RC
j
[a+1+z, a+w+n] ) For n = 0
→ H - a - w, z = f → 0 (we calculate the
maximum load that can be transferred).
¾ Transfer the maximum number of tasks from A
(using the approach described in the precedent
page) that the sum of their processing times is
inferior or equal to Cap. Let C be the set of these
tasks transferred and Q the sum of their
processing time:
∀ the task ij ∈ C, we put b
ij
= a+1 + f
For n = 0 → H - a - w and for z = f → 0, we do:
RC
j
[a+1+z, a+w+n] = RC
j
[a+1+z, a+w +n ] –
Q (We update the new time scheduling segment
of the tasks and the remaining capacity of the
concerned lapses).
- We update the beginning and the ending of the
scheduling time segments of the other tasks on the
other processors as follow:
¾ If a task u precedes task j of the same job i on
the processor j, we move its scheduling time
segment in a manner that the ending time
becomes equal to the beginning time of the task
j. We effectuate the same treatment until
arriving to the first task.
¾ If a task u follows task j of the same job i on the
processor j, we update in a symmetrically
manner the scheduling time segment of this
task and all the other tasks up to the last one.
5
th
step:
We assign all the unused margins to the next
processor (in this case the processor P1). We
calculate the scheduling time segments of the tasks
corresponding to this processor using the following
formulae:
∀ i , for a processor j :
b
ji
= e
ji
– M’a
i
- ⎡(p
ij
/ d
p
)⎤
+ 1
(3)
Where M’a
i
is the remaining margin.
We can assign margins for a task i on a
processor j only if the precedent tasks of the same
job are not already treated. We obtain the C.R.P. and
the control feasibility graph of the processor P1 as
follow:
Per iods
(
we e ks
)
1
2
3
4
5
A1
(
3
)
F1
(
3
)
G1
(
1
)
H1
(
2
)
I1
(
1
)
J1
(
3
)
L1
(
2
)
6
B1
(
2
)
C1
(
3
)
7
22
33
44
55
23
34
45
24
35
25
0
0
5
0
0
3
3
3
2
6
6
-1
0
0 10
3
0
7
9
0
1
0
0 15
12
3 3
12
0 8
Accumulated capacity (days)
5 10 15 20
66
0
0
5
56
8
2
2
46
9
0 6
36
14
0 6
26
14
0
11
25
11
0
0
5
12
5
5
13
5
0 10
14
8
0 12
47
12
0 8
77
1
1
4
67
1
0
9
46
11
0 4
37
15
0
10
15
17
0
8
27
15
0
15
16
19
0
11
17
20
0
15
30
35
5
Figure 7: CRP and PFCG of processor P1 after assigning
all the available margins.
We check then the feasibility condition. If for a
lapse [a,b] in the processor j, the validation
condition is not verified, we should lengthen the
scheduling time segment of the tasks as follows:
- We consider in the duration increasing order the
list of all the tasks included in the lapse [a,b] and
that b
ij
= a or e
ij
= b.
- In order to treat the minimum number of tasks, we
begin to treat in this list the first task in the k
th
position in the list which has a load equal or
superior to the overloading in the lapse.
- We try to regain a margin for this task by
shortening the scheduling time segment of the
precedent task of the same job in a processor
already treated.
- We try this for all the tasks positioned in the (k+1)
th
position in the list until succeeding or arriving to
the end of the list.
- If we arrive to the end of the list, we try with tasks
positioned in the (k-1)
th
, (k-2)
th
… position until
succeeding or arriving to the beginning of the list.
- We must lengthen the scheduling time segment of
as many tasks as necessary to validate the
feasibility of the problematic lapse.
- If the remaining capacity continues to be negative,
we reiterate the treatment of the tasks in the same
order but by trying in this case to move completely
if possible the precedent task of the same job in the
past which allows us to lengthen the scheduling
time segment of tasks of this processor.
- If we do not succeed, we treat the tasks in the same
order by trying to delay the due date on a minimum
number of jobs or by increasing the capacity of the
incriminate lapses.
If we take our example, the control feasibility
graph of the processor P1 indicates that we have a
problem in the lapse [5,5] (Figure 7): the
accumulated capacity requirement is 6 days and the
available capacity is 5 days, so we should lengthen
the scheduling time segment of one of the tasks F1
A NEW LOAD ADJUSTMENT APPROACH FOR JOB-SHOPS
281

or J1. If we lengthen the task in the right, the due
date order will be delayed (F1 or J1 are the last task
of the jobs F and J), so we will try to shorten or
move the scheduling time of F2 or J2 in the
processor P2. F2 can not be shortened (the
scheduling time segment is one period). J2 can be
shortened, the scheduling time segment will be
shortened to the lapse [2,3]. We verify that the
control feasibility graph of P2 remains valid. The
scheduling time segment of J1 will become [4,5].
The control feasibility graph of P1 becomes valid
and we can try to regain margins like done for the
processor P2 in the fourth step. We obtain the C.R.P.
of processor 1 as follow:
Periods
(
weeks
)
1 2 3 4 5
A1
(
3
)
F1
(
3
)
G1
(
1
)
H1
(
2
)
I1
(
1
)
J1
(
3
)
L1
(
2
)
6
B1
(
2
)
C1
(
3
)
7
Periods
(
weeks
)
2 3 4 5
A3
(
2
)
F3
(
2
)
G3
(
1
)
H3
(
2
)
I3
(
2
)
K3
(
4
)
L3
(
3
)
6
B3
(
1
)
E3
(
2
)
Figure 8: C.R.P. of processor P1 and P3 after treatment.
Then, we apply step 5 for the last processor P3
and we obtain the C.R.P. as shown in Figure 8. We
update the beginning and the ending of the
scheduling time segments of the other tasks on the
other processors as explained in step 4 and we obtain
the final CRP of processors P1 and P2:
Periods
(
weeks
)
2 3 4 5
A2(2)
F2(3)
G2(1)
H2(2)
I2(2)
J2(3)
K2(3)
6
B2(3)
D2(2)
Periods
(
weeks
)
2 3 4 5
A1
(
3
)
F1
(
3
)
G1
(
1
)
H1
(
2
)
I1
(
1
)
J1
(
3
)
L1
(
2
)
6
B1
(
2
)
C1
(
3
)
7
Figure 9: Final C.R.P. of processor P2 after treatment and
a possible scheduling solution.
4 SCHEDULING
In case where we admit to interrupt at least one task
by period, the overlapping load adjustment approach
furnishes a necessary and sufficient condition for the
existence of a feasible scheduling solution. The
scheduling will be made in a real time manner.
Indeed, in the end of each task the responsible will
choose the next task between all the tasks that can be
loaded and so on. This load adjustment approach
will be coupled with a scheduling tool which can
function as described below. If we take our example
of Figure 1, the real time scheduling can be made as
follow:
- In the beginning of week 2 we can choose to begin
the task F or B (Figure 1), we choose for instance
task B and then task F.
- We arrive at the end of day 1 of week 3 and we see
that we can choose between three tasks: A or D or
E (Figure 1). The scheduling tool will inform the
user if he could really choose one task and during
how much time without breaking the feasibility
condition. If the user chooses for example task A,
the scheduling tool will tell him that the task A can
be scheduled for only one day until the end of the
second day of the week because there are two tasks
E and D with a total duration of 3 days that must be
scheduled on week 3. So, if the user decides to
choose A, he must interrupt A after one day,
schedule E and D and after that, continue with the
task A, but the user can choose to schedule E and D
without interruption. We suppose that the user
chose the task E and so we obtain the partial
scheduling described in Figure 10.
- We continue in the same way the scheduling and
we can obtain for example the final scheduling of
Figure 10.
Periods (weeks)
W eek 2
W 3
E(2)
F(2)
B
(
4
)
Periods
(
weeks
)
W2
W3
W4 W5
E(2) F(2)
C(4)
A(2)
D(2)
B(4)
G(4)
Figure 10: the partial and final scheduling.
In our opinion, this original approach of
scheduling presents many advantages in comparison
with the automatic calculation of a schedule. First,
the approach is really dynamic, each decision is
taken in the last moment and we do not produce
plans which will be out of date. Moreover, the user
can have its own reasons to choose one task or
another. A system that proposes and does not impose
but exposes the consequences of each choice in
regard to the scheduling which allows the user to
decide with full knowledge of the facts and
integrates his own criteria. This characteristic could
promote the scheduling performance, and allow in
all cases the responsibility of the user and his
comprehension of the system.
5 EXPERIMENTATION
An experimentation has been carried out on a set of
examples. We’ll describe very briefly (due to edition
constraints) the conditions and the results of this
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
282

experimentation. We have constructed 20 examples
where we varied the number of jobs (5 to 20) and the
number of processors (2 to 4). The total load is
always near or superior to the capacity. We
compared our approach with the classic approach of
placement. For each example, we apply our
approach and the placement approach. This
placement is applied in two steps: first an earliest
placement to determine the earliest due dates and
second a latest placement using job’s due dates as
the maximum between the requested due dates and
the earliest ones. We have compared the two
approaches in terms of number of jobs delayed. The
percentage of jobs delayed with the placement is
about 25 % whereas it is equal to 8 % with our
approach. This fact proves really the efficiency of
our approach. However, we should experiment and
compare our approach with other approaches.
6 CONCLUSIONS
We think that the most common approach used in
production planning remains MRP II
(Manufacturing Resource Planning). The proposed
approach in this paper works in a hierarchical
production planning and scheduling and constitutes
an alternative to the traditional load adjustment
approaches used in the CRP (Capacity Requirement
Planning) modules in software based on MRP II
philosophy. The new heuristic presented in this
paper, in comparison with the usual middle and/or
long-term planning and scheduling approaches, has
the following advantages:
- not setting a long-term tasks scheduling to assure
that the planning can be properly carried out;
- exploiting the intrinsic margins of each job to
obtain their loading time segments guaranteeing the
production planning feasibility under the
assumption of pre-emptive tasks;
- distributing judiciously the job’s margins on their
tasks and trying to respect the just-in-time
principles;
- splitting up the production planning into jobs
subsets making thus its analysis and its exploitation
easier;
- permitting the postponement of the final scheduling
jobs problem until the short term at the order
release phase and/or the scheduling phase;
- delaying, if necessary, the due dates of some jobs
or increasing the capacity in some lapses for
guaranteeing in every case the feasibility of the
production planning.
We can extend and improve our work by
studying the possibility of introducing the
overlapping of the scheduling time segments of
consecutive tasks. We can also improve our heuristic
accordingly since we want to minimize the average
tardiness or the max tardiness or the number of
delayed jobs.
REFERENCES
Bahroun, Z., Jebali, D., Baptiste, P., Campagne, J-P. and
Moalla, M.,
1999. Extension of the overlapping
production planning and application for the cyclic
delivery context, in IEPM ‘99 Industrial Engineering
and Production Management, Glasgow
.
Bahroun, Z., Campagne, J-P. and Moalla, M., 2000a. The
overlapping production planning: A new approach of a
limited capacity management
. International Journal of
Production Economics
, 64, 21-36.
Bahroun, Z., Campagne, J-P. and Moalla, M., 2000b. Une
nouvelle approche de planification à capacité finie
pour les ateliers flow-shop. Journal Européen des
Systèmes Automatisés
, 5, 567-598.
Dauzere-Peres, S., and Lassere, J-B., On the importance of
scheduling decisions in production planning and
scheduling. International Transactions in Operational
Research, 9(6), 779-793.
Dillenseger, F., 1993. Conception d'un système de
planification à moyen terme pour fabrications à la
commande. PhD thesis, INSA Lyon, France.
Drexl, A. and Kimms, A., 1997. Lot sizing and scheduling
- Survey and extensions. European Journal of
Operation Research, 99, 221-235.
Fleischmann, B. and Meyr, H., 1997. The general lot
sizing and scheduling problem. Operation Research
Spektrum, 19(1), 11-21.
Gunther, H.O., 1987. Planning lot sizes and capacity
requirements in a single stage production system.
European Journal of Operational Research, 31(1),
223-231.
Hillion, H. and Proth, J-M., 1994. Finite capacity flow
control in a multi-stage/multi-product environment.
International Journal of production Research, 32(5),
1119-1136.
Néron, E., Baptiste, P. and Gupta, J.N.D., 2001. Solving
Hybrid Flow Shop problem using energetic reasoning
and global operations. Omega, 29, 501-511.
A NEW LOAD ADJUSTMENT APPROACH FOR JOB-SHOPS
283
