A MODIFIED IMPULSE CONTROLLER FOR IMPROVED

ACCURACY OF ROBOTS WITH FRICTION

Stephen van Duin, Christopher D. Cook, Zheng Li and Gursel Alici

Faculty of Engineering, University of Wollongong, Northfields Avenue, Gwynnville, Australia

Keywords: Impulsive control, static friction, limit cycle, stick-slip, impulse shape, friction model, accuracy.

Abstract: This paper presents a modified

impulse controller to improve the steady state positioning of a SCARA robot

having characteristics of high non-linear friction. A hybrid control scheme consisting of a conventional PID

part and an impulsive part is used as a basis to the modified controller. The impulsive part uses short width

torque pulses to provide small impacts of force to overcome static fiction and move a robot manipulator

towards its reference position. It has been shown that this controller can greatly improve a robot’s accuracy.

However, the system in attempting to reach steady state will inevitably enter into a small limit cycle whose

amplitude of oscillation is related to the smallest usable impulse. It is shown in this paper that by modifying

the impulse controller to adjust the width of successive pulses, the limit cycle can be shifted up or down in

position so that the final steady state error can be even further reduced.

1 INTRODUCTION

Precision robot manufacturers continually strive to

increase the accuracy of their machinery in order to

remain competitive. The ability of a robot

manipulator to position its tool centre point to within

a very high accuracy, allows the robot to be used for

more precise tasks. For positioning of a tool centre

point, the mechanical axes of a robot will be

required to be precisely controlled around zero

velocity where friction is highly non-linear and

difficult to control.

Non-linear friction is naturally present in all

mechanism

s and can cause stick-slip during precise

positioning. In many instances, stick-slip has been

reduced or avoided by modifying the mechanical

properties of the system; however this approach may

not always be practical or cost effective.

Alternatively, advances in digital technology have

made it possible for the power electronics of

servomechanisms to be controlled with much greater

flexibility. By developing better controllers, the

unfavourable effects of non-linear friction may be

reduced or eliminated completely.

Impulse control has been successfully used for

accurate positioni

ng of servomechanisms with high

friction where conventional control schemes alone

have difficulty in approaching zero steady state

error. Static and Coulomb friction can cause a

conventional PID controller having integral action

(I), to overshoot and limit cycle around the reference

position. This is a particular problem near zero

velocities where friction is highly non linear and the

servomechanism is most likely to stick-slip. Despite

the above difficulties, PID controllers are still

widely used in manufacturing industries because of

their robustness to parameter uncertainty and

unknown disturbances.

Stick-slip can be reduced or eliminated by using

mpulsive control near or at zero velocities. The

impulsive controller is used to overcome static

friction by impacting the mechanism and moving it

by microscopic amounts. By combining the

impulsive controller and conventional controller

together, the PID part can be used to provide

stability when moving towards the reference

position while the impulse controller is used to

improve accuracy for the final positioning where the

error signal is small.

By applying a short impulse of sufficient force

lastic deformation occurs between the asperities of

mating surfaces resulting in permanent controlled

movement. If the initial pulse causes insufficient

movement, the impulsive controller produces

additional pulses until the position error is reduced

to a minimum.

165

van Duin S., D. Cook C., Li Z. and Alici G. (2007).

A MODIFIED IMPULSE CONTROLLER FOR IMPROVED ACCURACY OF ROBOTS WITH FRICTION.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 165-173

DOI: 10.5220/0001618901650173

 SciTePress

Figure 1: Bristle model; Figure a) shows the deflection of a

single bristle. Figure b) shows the resulting static friction

model for a single instance in time.

A number of investigators have devised

impulsive controllers which achieve precise motion

in the presence of friction by controlling the height

or width of a pulse. Yang and Tomizuka (Yang et al,

1988) applied a standard rectangular shaped pulse

whereby the height of the pulse is a force about 3 to

4 times greater than the static friction to guarantee

movement. The width of the pulse is adaptively

adjusted proportional to the error and is used to

control the amount of energy required to move the

mechanism towards the reference positioning.

Alternatively, Popovic (Popovic et al, 2000)

described a fuzzy logic pulse controller that

determines both the optimum pulse amplitude and

pulse width simultaneously using a set of

membership functions. Hojjat and Higuchi (Hojjat

et al, 1991) limited the pulse width to a fixed

duration of 1ms and vary the amplitude by applying

a force about 10 times the static friction. Rathbun et

al (Rathbun et al, 2004) identify that a flexible-body

plant can result in a position error limit cycle and

that this limit cycle can be eliminated by reducing

the gain using a piecewise-linear-gain pulse width

control law.

In a survey of friction controllers by Armstrong-

Hélouvry (Armstrong- Hélouvry et al, 1994), it is

commented that underlying the functioning of these

impulsive controllers is the requirement for the

mechanism to be in the stuck or stationary position

before subsequent impulses are applied. Thus,

previous impulse controllers required each small

impacting pulse to be followed by an open loop slide

ending in a complete stop.

Figure 2: The Hirata SCARA robot.

Figure 3: Block diagram of the experimental system

controller.

In this paper, a hybrid PID + Impulsive

controller is used to improve the precision of a

servomechanism under the presence of static and

Coulomb friction. The design and functioning of the

controller does not require the mechanism to come

to rest between subsequent pulses, making it suitable

for both point to point positioning and speed

regulation. The experimental results of this paper

show that the shape of the impulse can be optimised

to increase the overall precision of the controller. It

is shown that the smallest available movement of the

servomechanism can be significantly reduced

without modification to the mechanical plant.

2 MODELLING AND

EXPERIMENTAL SYSTEM

2.1 Friction Model

On a broad scale, the properties of friction are both

well understood and documented. Armstrong-

Hélouvry (Armstrong- Hélouvry et al, 1994) have

surveyed some of the collective understandings of

how friction can be modelled to include the

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

166

complexities of mating surfaces at a microscopic

level. Canudas de Wit (Canudas de Wit et al, 1995)

add to this contribution by presenting a new model

that more accurately captures the dynamic

phenomena of rising static friction (Rabinowicz,

1958), frictional lag (Rabinowicz, 1958), varying

break away force (Johannes et al, 1973),

(Richardson et al, 1976), dwell time (Kato et al,

1972), pre-sliding displacement (Dahl, 1968), (Dahl,

1977), (Johnson, 1987) and Stribeck effect (Olsson,

1996). The friction interface is thought of as a

contact between elastic bristles. When a tangential

force is applied, the bristles deflect like springs

which give rise to the friction force (Canudas de Wit

et al, 1995); see Figure 1(a). If the effective applied

force F

exceeds the bristles force, some of the

bristles will be made to slip and permanent plastic

movement occurs between each of the mating

surfaces. The set of equations governing the

dynamics of the bristles are given by (Olsson, 1996):

()

−= (1)

() ()

()

(

CsC

gv F F F e

−

=+−

)

(2)

()

vzF

++=

σσ

(3)

()

σσ

−

(4)

where v is the relative velocity between the two

surfaces and z is the average deflection of the

bristles.

is the bristle stiffness and σ

is the bristle

damping. The term v

is used to introduce the

velocity at which the Stribeck effect begins while

the parameter v

determines the velocity interval

around zero for which the velocity damping is

active. Figure 1(b) shows the friction force as a

function of velocity. F

is the average static friction

while F

is the average Coulomb friction. For very

low velocities, the viscous friction F

is negligible

but is included for model completeness. F

, F

, and

are all estimated experimentally by subjecting a

real mechanical system to a series of steady state

torque responses. The parameters

and v

are

also determined by measuring the steady state

friction force when the velocity is held constant

(Canudas de Wit et al, 1995).

2.2 Experimental System

For these experiments, a Hirata ARi350 SCARA

(Selective Compliance Assembly Robot Arm) robot

was used. The Hirata robot has four axes named A,

B, Z and W. The main rotational axes are A-axis

(radius 350mm) and B-axis (radius 300mm) and

they control the end-effector motion in the

horizontal plane. The Z-axis moves the end-effector

in the vertical plane with a linear motion, while the

W-axis is a revolute joint and rotates the end effector

about the Z-axis. A photograph of the robot is

shown in Figure 2.

For these experiments, only the A and B axis of

the Hirata robot are controlled. Both the A and B

axes have a harmonic gearbox between the motor

and robot arm. Their gear ratios are respectively

100:1 and 80:1. All of the servomotors on the Hirata

robot are permanent magnet DC type and the A and

B axis motors are driven with Baldor® TSD series

DC servo drives. Each axis has characteristics of

high non-linear friction whose parameters are

obtained by direct measurement. For both axes, the

static friction is approximately 1.4 times the

Coulomb friction.

Matlab’s xPC target oriented server was used to

provide control to each of the servomotor drives. For

these experiments, each digital drive was used in

current control mode which in effect means the

output voltage from the 12-bit D/A converter gives a

torque command to the actuator’s power electronics.

The system controller was compiled and run using

Matlab’s real time xPC Simulink® block code. A

12-bit A/D converter was used to read the actuator’s

shaft encoder position signal.

2.3 PID + Impulse Hybrid Controller

Figure 3 shows the block diagram of a PID linear

controller + impulsive controller. This hybrid

controller has been suggested by Li (Li et al, 1998)

whereby the PID driving torque and impulsive

controller driving torque are summed together. It is

unnecessary to stop at the end of each sampling

period and so the controller can be used for both

position and speed control.

The controller can be divided into two parts; the

upper part is the continuous driving force for large

scale movement and control of external force

disturbances. The lower part is an additional

proportional controller k

pwm

with a pulse width

modulated sampled-data hold (PWMH), and is the

basis of the impulsive controller for the control of

stick-slip.

A MODIFIED IMPULSE CONTROLLER FOR IMPROVED ACCURACY OF ROBOTS WITH FRICTION

167

The system controller is sampled at 2 kHz. The

impulse itself is sampled and applied at one

twentieth of the overall sampling period (i.e. 100

Hz) to match the mechanical system dynamics.

Figure 4 shows a typical output of the hybrid

controller for one impulse sampling period

. The

pulse with height f

is added to the PID output.

Because the PID controller is constantly active, the

PID

Output

Figure 4: Friction controller output.

system has the ability to counteract random

disturbances applied to the servomechanism. The

continuous part of the controller is tuned to react to

large errors and high velocity, while the impulse part

is optimized for final positioning where stiction is

most prevalent.

For large errors, the impulse width approaches

the full sample period

, and for very large errors, it

transforms into a continuous driving torque. When

this occurs, the combined control action of the PID

controller and the impulsive controller will be

continuous. Conversely, for small errors, the PID

output is too small to have any substantial effect on

the servomechanism dynamics.

The high impulse sampling rate, combined with a

small error, ensures that the integral (I) part of the

PID controller output has insufficient time to rise

and produce limit cycling. To counteract this loss of

driving torque, when the error is below a threshold,

the impulsive controller begins to segment into

individual pulses of varying width and becomes the

primary driving force. One way of achieving this is

to make the pulse width Δ determined by:

spwm

kek

)(⋅

=Δ

|||)(|k

pwm p

fke

≤

⋅

=Δ

otherwise (6)

In (6)

(

()

)

fsignek=⋅

(7)

where e(k) is the error input to the controller, |f

is a fixed pulse height greater than the highest static

friction and

is the overall sampling period. For

the experimental results of this paper, the impulsive

sampling period

was 10ms and the pulse width

could be incrementally varied by 1ms intervals. The

pulse width gain k

pwm

, is experimentally determined

by matching the mechanism’s observed

displacement d to the calculated pulse width t

using

the equation of motion:

()

pp C

ff f

−

, f

> 0 (8)

The gain is iteratively adjusted until the net

displacement for each incremental pulse width is as

small as practical.

2.4 Minimum Pulse Width

The precision of the system is governed by the

smallest incremental movement which will be

produced from the smallest usable width pulse.

Because the shape of the pulse is affected by the

system’s electrical circuit response, a practical limit

is placed on the amplitude of the pulse over very

short durations and this restricts the amount of

energy that can be contained within a very thin

pulse. Consequently, there exists a minimum pulse

width that is necessary to overcome the static

friction and guarantee plastic movement.

For the Hirata robot, the minimum pulse width

guaranteeing plastic displacement was determined to

be 2ms and therefore the pulse width is adjusted

between 2 and 10ms. Any pulse smaller than 2ms

results in elastic movement of the mating surfaces in

the form of pre-sliding displacement. In this regime,

short impulses can produce unpredictable

displacement or even no displacement at all. In some

cases, the mechanism will spring back greater than

the forward displacement resulting in a larger error.

Figure 5 shows the displacement of the experimental

system of five consecutive positive impulses

followed by five negative impulses. The experiment

compares impulses of width 2ms and 1.5ms. For

impulses of 2ms, the displacement is represented by

the consistent staircase movement. For a width of

1.5ms, the displacement is unpredictable with

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

168

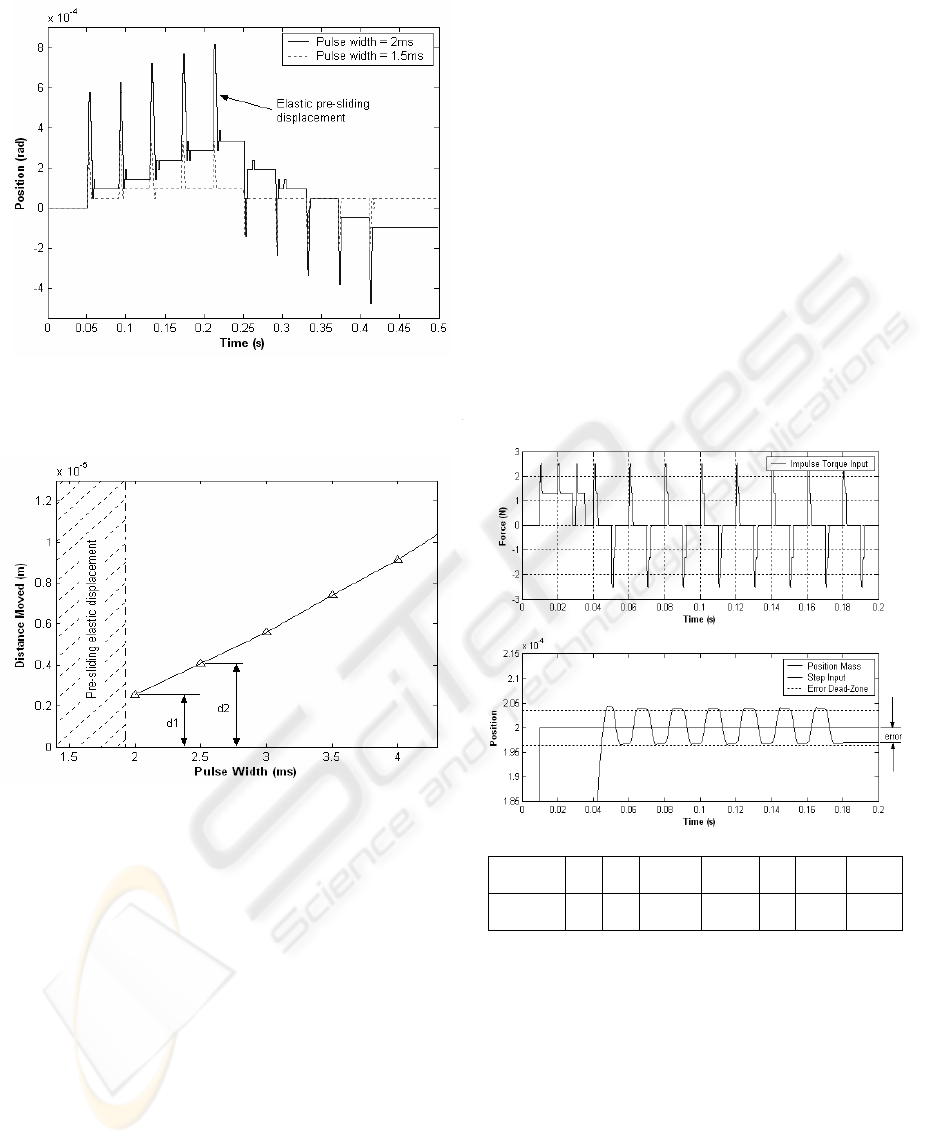
Figure 5: Experimentally measured displacement for both

positive and negative impulses using successive pulse

widths 1.5ms and 2ms.

Figure 6: Simulated displacements as a function of pulse

width.

mostly elastic pre-sliding movement which results in

zero net displacement.

Wu et al (Wu et al, 2004) use the pre-sliding

displacement as a means to increase the precision of

the controller by switching the impulse controller off

and using a continuous ramped driving torque to

hold the system in the desired position. The torque is

maintained even after the machine is at rest. This is

difficult in practice as pre-sliding movement must be

carefully controlled in the presence of varying static

friction so that inadvertent breakaway followed by

limit cycling is avoided.

3 LIMIT CYCLE OFFSET

3.1 Motivation

Figure 6 shows the simulated displacements of

varying pulse widths which have been labelled d1,

d2, d3…dn respectively, where d1 is the minimum

pulse width which will generate non elastic

movement and defines the system’s resolution.

Using the variable pulse width PID + impulse

controller for a position pointing task, the torque will

incrementally move the mechanism towards the

reference set point in an attempt to reach steady

state. Around the set point, the system will

inevitably begin to limit cycle when the error e(k) is

approximately the same magnitude as the system

resolution (the displacement for the minimum pulse

width d1).

Figure 7: Simulation of the impulse controller limit

cycling around a position reference set-point where the

final torque output is a pulse with a minimum width and

the mean peak to peak oscillation is d1. The friction

parameters used for the simulation are also given in the

accompanying table.

For the limit cycle to be extinguished, the

controller must be disabled. As an example, the limit

cycle in Figure 7 is extinguished by disabling the

impulse controller at t=0.18s, and in this case, the

resulting error is approximately half the

displacement of the minimum pulse width d1.

Parameter F

Value 2 1 4.5*10

12,000 0.4 0.001 0.0004

A MODIFIED IMPULSE CONTROLLER FOR IMPROVED ACCURACY OF ROBOTS WITH FRICTION

169

Limit cycling will occur for all general

servomechanisms using a torque pulse because

every practical system inherently has a minimum

pulse width that defines the system’s resolution.

Figure 7 simulates a typical limit cycle with a peak

to peak oscillation equal to the displacement of the

minimum pulse width d1.

One way to automatically extinguish the limit

cycle is to include a dead-zone that disables the

controller output when the error is between an upper

and lower bound of the reference point (see Figure

7). The final error is then dependent on the amount

of offset the limit cycle has in relation to the

reference point. Figure 7 shows a unique case where

the ± amplitude of the limit cycle is almost evenly

distributed either side of the reference set point; i.e.

the centre line of the oscillation lies along the

reference set point. In this instance, disabling the

controller would create an error e(k) equal to

approximately

. This however, would vary in

practice and the centreline is likely to be offset by

some arbitrary amount. The maximum precision of

the system will therefore be between d1 and zero.

reference

position

d2 - d1

new

error

Time

Position

Figure 8: Conceptual example of reducing the steady state

error using ‘Limit Cycle Offset’ with the limit cycle shifted

up by d2-d1 and the new error that is guaranteed to fall

within the dead-zone.

3.2 Limit Cycle Offset Function

By controlling the offset of the limit cycle

centreline, it is possible to guarantee that the final

error lies within the dead-zone, and therefore to

increase the precision of the system. As a conceptual

example, Figure 8 shows a system limit cycling

either side of the reference point by the minimum

displacement d1. By applying the next smallest

pulse d2, then followed by the smallest pulse d1, the

limit cycle can be shifted by d2 – d1. The effect is

that the peak to peak centreline of the oscillation has

now been shifted away from the reference point.

However, at least one of the peaks of the

oscillation has been shifted closer to the set point. If

the controller is disabled when the mechanism is

closest to the reference set point, a new reduced

error is created. For this to be realised, the

incremental difference in displacement between

successively increasing pulses must be less than the

displacement from the minimum pulse width; for

example d2 – d1 < d1.

3.3 Modified Controller Design

For the limit cycle to be offset at the correct time,

the impulse controller must have a set of additional

control conditions which identify that a limit cycle

has been initiated with the minimum width pulse.

The controller then readjusts itself accordingly using

a ‘switching bound’ and finally disables itself when

within a new specified error ‘dead-zone’. One way

to achieve this is to adjust the pulse width so that it

is increased by one increment when satisfying the

following conditions:

if switching bound > |e(k)| ≥ dead-zone

then

()

pwm s

kek

⋅

otherwise

()

wm s

kek

⋅

Δ=

(9)

where the switching bound is given by:

|switching bound| <

(10)

and the dead-zone is given by:

(d2 - d1)

dead-zone =

(11)

The steady state error e(k) becomes:

steady state

deadzone

e(k)

≤

(12)

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

170

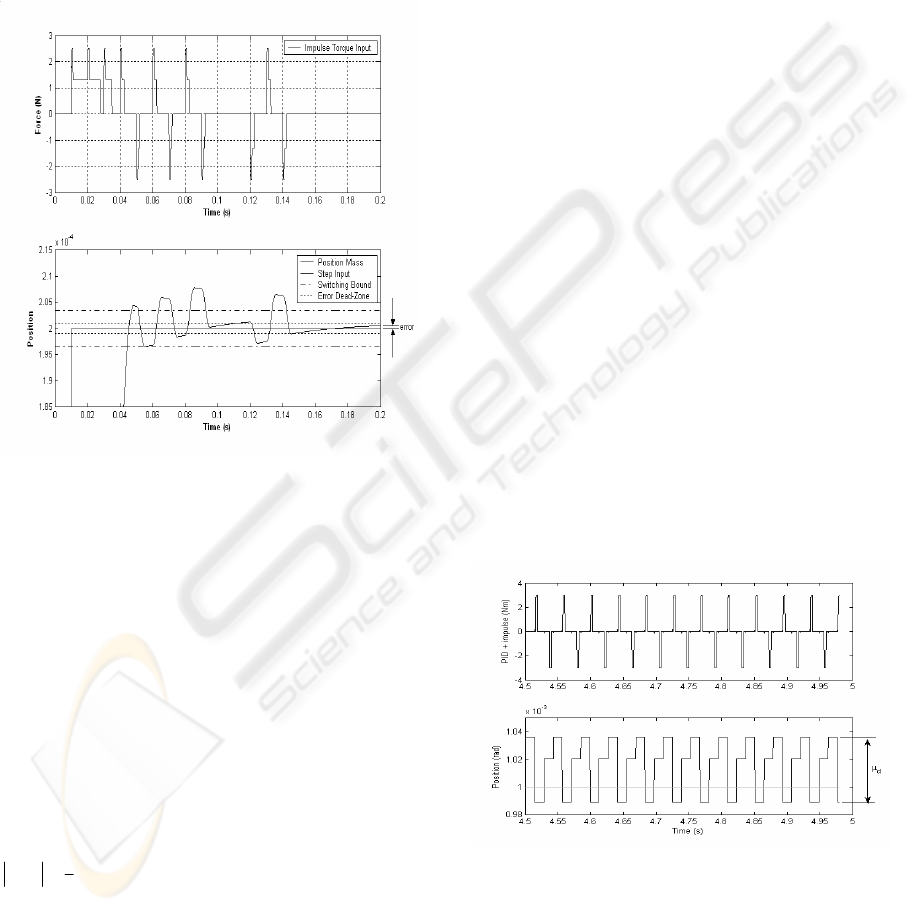
3.4 Simulation of the Limit Cycle

Offset Function

To demonstrate the limit cycle offset function, the

modified controller is simulated using a simple unit

mass with the ‘new’ friction model using Eqs. 1 to 4.

A simulated step response is shown in Figure 9

to demonstrate how the modified controller works.

Here the mechanism moves towards the reference

set point and begins limit cycling. Because at least

Figure 9: Simulation of the limit cycle offset function

used with the PID + impulse controller.

one of the peaks of the limit cycle immediately lies

within the switching bound, the controller shifts the

peak to peak oscillation by d2 - d1 by applying the

next smallest pulse, and then followed by the

smallest pulse. In this example, the first shift is

insufficient to move either peak into the set dead-

zone so the controller follows with a second shift. At

time 0.1 seconds, the controller is disabled;

however, the elastic nature of the friction model

causes the mechanism’s position to move out of the

dead-zone. As a result, the controller is reactivated

(time 0.12s) and the controller follows with a third

shift. In this instance, the mechanism reaches steady

state at t=0.2s, and the final error is

( ) (dead zone)ek ≤⋅

which in this case is ± 1e-6

radians. A final analysis of the result shows that the

new controller has reduced the error by an amount

significantly more than a standard impulse

controller. This reduction correlates directly to the

improvement in the system’s accuracy by a factor of

4 EXPERIMENTAL

4.1 Position Pointing

This section evaluates the limit cycle offset function

using the experimental Hirata robot having position

dependent variables. Figure 10 shows a steady state

limit cycle for a position pointing step response of

0.001 radians using a PID + impulse hybrid

controller. The mean peak to peak displacement of

the smallest non-elastic part of the limit cycle is μ

The experiment was repeated using the limit

cycle offset function with the same position step

reference of 0.001 radians. Figure 11 shows a

sample experiment and in this example, the limit

cycle offset function is activated at t=0.9s. At this

time, the amplitude of the non elastic part of the

limit cycle is identified as lying between the

switching bounds. The switching bounds and dead-

zone are set according to the methodology given

earlier. Once the offset function is activated, the

controller adjusts itself by forcing the proceeding

pulse to be one increment wider before returning to

the smallest pulse width. This results in the limit

cycle being shifted down into the dead-zone region

where the impulse controller is automatically

disabled at t=0.95s. At this time, the final error is

guaranteed to fall within the error dead zone which

can be seen from Fig 11 to be in the vicinity of ±1e-

4 radians.

Figure 10: Steady state limit cycle for the PID + impulse

hybrid controller when applying a unit step input to the

Hirata robot. The mean peak to peak displacement μ

the non-elastic part of limit cycle.

A MODIFIED IMPULSE CONTROLLER FOR IMPROVED ACCURACY OF ROBOTS WITH FRICTION

171

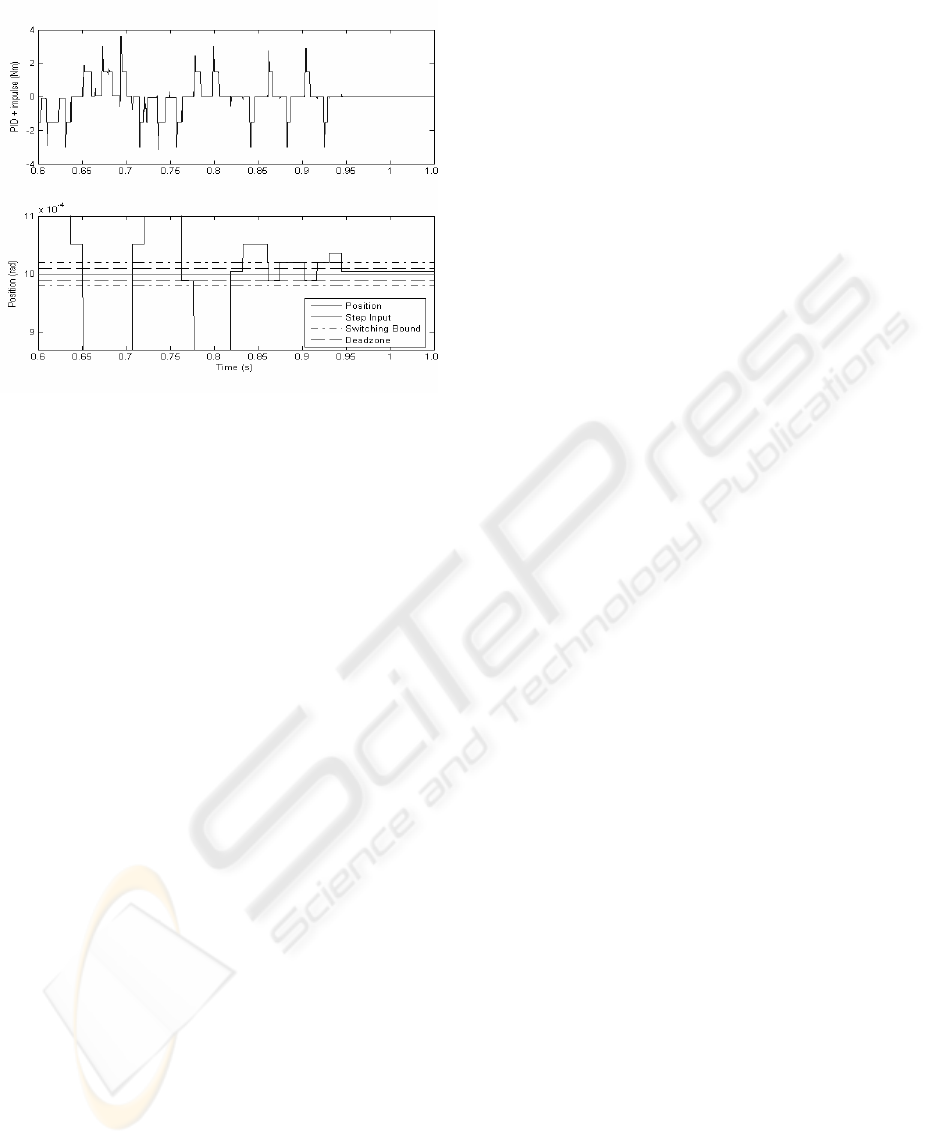
Figure 11: Using the ‘Limit Cycle Offset’ function to

reduce the final steady state error of the Hirata robot.

4.2 Discussion of Results

This set of results demonstrates the Limit Cycle

Offset function can be successfully applied to a

commercial robot manipulator having characteristics

of high non-linear friction. The results show that the

unmodified controller will cause the robot to limit

cycle near steady state position and that the peak to

peak displacement is equal to the displacement of

the smallest usable width pulse.

By using the Limit Cycle Offset function, the

limit cycle can be detected and the pulse width

adjusted so that at least one of the peaks of the limit

cycle is moved towards the reference set point.

Finally, the results show that the controller

recognises the limit cycle as being shifted into a

defined error dead-zone whereby the controller is

disabled. The steady state error is therefore

guaranteed to fall within a defined region so that the

steady state error is reduced. For the SCARA robot,

the improvement in accuracy demonstrated was

1.1e-4 radians in comparison to 4.5e-4 radians

achieved without the limit cycle offset.

5 CONCLUSION

Advances in digital control have allowed the power

electronics of servo amplifiers to be manipulated in

a way that will improve a servomechanism precision

without modification to the mechanical plant. This is

particularly useful for systems having highly non-

linear friction where conventional control schemes

alone under perform. A previously developed hybrid

PID + Impulse controller which does not require the

mechanism to come to a complete stop between

pulses has been modified to further improve

accuracy. This modification shifts the limit cycling

into a different position to provide substantial

additional improvement in the mechanism’s position

accuracy. This improvement has been demonstrated

both in simulations and in experimental results on a

SCARA robot arm. The mechanism does not have to

come to a complete stop between pulses, and no

mechanical modification has to be made to the robot.

REFERENCES

Armstrong-Hélouvry, B., 1991, “Control of Machines with

Friction” Kluwer Academic Publishers, 1991, Norwell

MA.

Armstrong-Hélouvry, B., Dupont, P., and Canudas de

Wit, C., 1994, “A survey of models, analysis tools and

compensation methods for the control of machines

with friction” Automatica, vol. 30(7), pp. 1083-1138.

Canudas de Wit, C., Olsson, H., Åström, K. J., 1995 ”A

new model for control of systems with friction” IEEE

Tansactions on Automatic Control, vol. 40 (3), pp.

419-425.

Dahl, P., 1968, “A solid friction model” Aerospace Corp.,

El Segundo, CA, Tech. Rep. TOR-0158(3107-18)-1.

Dahl, P, 1977, “Measurement of solid friction parameters

of ball bearings” Proc. of 6

annual Symp. on

Incremental Motion, Control Systems and Devices,

University of Illinois, ILO.

Hojjat, Y., and Higuchi, T., 1991 “Application of

electromagnetic impulsive force to precise

positioning” Int J. Japan Soc. Precision Engineering,

vol. 25 (1), pp. 39-44.

Johannes, V. I.., Green, M.A., and Brockley,C.A., 1973,

“The role of the rate of application of the tangential

force in determining the static friction coefficient”,

Wear, vol. 24, pp. 381-385.

Johnson, K.L., 1987, “Contact Mechanics” Cambridge

University Press, Cambridge.

Kato, S., Yamaguchi, K. and Matsubayashi, T., 1972,

“Some considerations of characteristics of static

friction of machine tool slideway” J. o Lubrication

Technology, vol. 94 (3), pp. 234-247.

Li, Z, and Cook, C.D., 1998, ”A PID controller for

Machines with Friction” Proc. Pacific Conference on

Manufacturing, Brisbane, Australia, 18-20

August,

1998, pp. 401-406.

Olsson, H., 1996, “Control Systems with Friction”

Department of Automatic Control, Lund University,

pp.46-48.

Popovic, M.R., Gorinevsky, D.M., Goldenberg, A.A.,

2000, “High precision positioning of a mechanism

with non linear friction using a fuzzy logic pulse

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

172

controller” IEEE Transactions on Control Systems

Technology, vol. 8 (1) pp. 151-158.

Rabinowicz, E., 1958, “The intrinsic variables affecting

the stick-slip process,” Proc. Physical Society of

London, vol. 71 (4), pp.668-675.

Rathbun, D,. Berg, M. C., Buffinton, K. W., 2004,

“Piecewise-Linear-Gain Pulse Width Control for

Precise Positioning of Structurally Flexible Systems

Subject to Stiction and Coulomb Friction”, ASME J

.of Dynamic Systems, Measurement and Control,

vol. 126, pp. 139-126.

Richardson, R. S. H., and Nolle, H., 1976, “Surface

friction under time dependant loads” Wear, vol. 37

(1), pp.87-101.

Wu, R,. Tung, P., 2004, “Fast Positioning Control for

Systems with Stick-Slip Friction”, ASME J .of

Dynamic Systems, Measurement and Control, vol.

126, pp. 614-627.

Yang, S., Tomizuka, M., 1988, “Adaptive pulse width

control for precise positioning under the influence of

stiction and Coulomb friction” ASME J .of Dynamic

Systems, Measurement and Control, vol. 110 (3), pp.

221-227.

A MODIFIED IMPULSE CONTROLLER FOR IMPROVED ACCURACY OF ROBOTS WITH FRICTION

173