A MULTI CRITERIA EVALUATION OVER A FINITE SCALE

FOR MAINTENANCE ACTIVITIES OF A MOTORWAY

OPERATOR

Céline Sanchez

(1)

, Jacky Montmain

(2)

, Marc Vinches

(2)

and Brigitte Mahieu

(1)

Service Structure Viabilité Sécurité, Société des Autoroutes Estérel Côtes d’Azur Provence Alpes

avenue de cannes, 06211 Mandelieu Cedex, France

(2)

Ecole des Mines d’Alès,6 avenue de Clavières, 30319 Alès Cedex, France

Keywords: Multi-criteria decision-making, Multi-criteria aggregation, Finite scale, Decision support system, Motorway

infrastructure.

Abstract: The Escota Company aims at the formalization and improvement of the decisional process for preventive

maintenance in a multi criteria (MC) environment. According to available pieces of knowledge on the

infrastructure condition, operations are to be evaluated with regards to (w.r.t.) technical but also to

conformity, security and financial criteria. This MC evaluation is modelled as the aggregation of partial

scores attributed to an operation w.r.t. a given set of n criteria. The scores are expressed over a finite scale

which can cause some troubles when no attention is paid to the aggregation procedure. This paper deals

with the consistency of the evaluation process, where scores are expressed as labels by Escota’s experts,

whereas the aggregation model is supposed to deal with numerical values and cardinal scales. We try to

analyse this curious but common apparent paradox in MC evaluation when engineering contexts are

concerned. A robustness study of the evaluation process concludes this paper.

1 ESCOTA DECISION PROCESS

1.1 Context

The Escota Company, founded in 1956, is the

leading operator of toll motorways in France. Due to

its integration into the Provence-Alpes-Côte d'Azur

region, Escota is committed, as every motorway

operator, to a sustainable development approach,

including the social, economic and environmental

aspects of its activities. Every year, specific

initiatives are undertaken, or repeated, to include the

motorway network in a sustainable development

approach. Within this scope, the Escota Company

aims at the formalization and improvement of the

decisional process for preventive maintenance and

property management in a multi actors and multi

criteria (MC) environment. These decisions concern

upkeep, improvement and upgrading operations,

involving technical, conformity, security or financial

criteria. The operations are related to operating

domains such as constructive works, carriageways,

vertical roadsigns and carriageway markings,

buildings, prevention of fire risks, open spaces…

Managing such a complex infrastructure necessitates

a dynamic Information Processing System (IPS) to

facilitate the way decision-makers use their

reasoning capabilities through adequate information

processing procedure.

1.2 Valuation of the Infrastructure

Condition

Periodic inspections are performed to detect and

measure, as early as possible, any malfunction

symptoms affecting an element of the infrastructure

(EI). The expert in charge of an operating domain

then analyses the technical diagnosis relative to the

EI. He evaluates the situation seriousness in terms of

technical risk analyses. This evaluation relies on a

specific set of n criteria relative to his domain. An

aggregation with a weighted arithmetic mean

(WAM) is then performed to assess a global degree

of emergency to the corresponding maintenance

operation. This evaluation is then submitted to the

official in charge of the operating network. This

Sanchez C., Montmain J., Vinches M. and Mahieu B. (2007).

A MULTI CRITERIA EVALUATION OVER A FINITE SCALE FOR MAINTENANCE ACTIVITIES OF A MOTORWAY OPERATOR.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 68-76

 SciTePress

latter coordinates the experts’ needs and demands

for operation planning purposes.

This paper deals more particularly with the MC

evaluation process by the expert of an operating

domain, i.e. the affectation of an emergency degree

to an operation. There exist several methods to

identify and perform aggregation process with a

WAM. The Analytic Hierarchical Process, AHP, is

probably the most famous one in industry (Saaty,

1980). However, because it explicitly guarantees the

consistency between the commensurable scales it

aggregates and the WAM operator it identifies, the

Measuring Attractiveness by a Categorical Based

Evaluation TecHnique method, MACBETH, has got

recent successes (Bana e Costa, 1994)(Clivillé,

2004). In our application, MACBETH is first used to

build the valuation scale associated to each

emergency criterion of a domain. It is then applied

to determine the WAM parameters.

Furthermore, the way experts give their

assessment in natural language raises another

problem (Jullien, 2006). These labels are commonly

converted into numerical values to perform the

aggregation process. No particular attention is

generally paid to this “translation”. However the

consequences over the aggregation results are

damageable. In civil engineering, the culture of

numbers is strongly developed. People commonly

manipulate symbolic labels but may convert them

into more or less arbitrary numerical values when

necessary without further care. This cultural

viewpoint explains why an aggregation operator is

generally preferred to a rule base whereas appraisals

are expressed in terms of symbolic labels (Jullien,

2006). A completely symbolic evaluation over finite

scales could be envisaged (Grabisch, 2006).

Let us illustrate the scales problem with the

following example. Let us suppose that the semantic

universe of an expert w.r.t. the seriousness of a

symptom is: {insignificant, serious, alarming}. We

can imagine that a corresponding possible set of

discrete numerical values (in [0; 1]) could be: {0;

0.5; 1}. There are several assumptions behind this

translation concerning the nature of the scale. This

point will be discussed later. Let us just note here

that the numerical values are commonly chosen

equidistant. Now let us consider another semantic

universe: {insignificant, minor, alarming}. This

time, the associated set of numerical values {0; 0.5;

1} intuitively appears more questionable. The expert

should prefer {0; 0.25; 1}. When seriousness

degrees of several symptoms are to be aggregated,

the result of the WAM aggregation strongly depends

on the choice of the set of numerical values.

Furthermore, in any case, the numerical WAM value

does not necessary belong to {0; 0.5; 1} or {0; 0.25;

1}. It must then be converted into the convenient

label in return.

The way labels are converted into numerical

values (and back) coupled to the commensurability

of the scales of the dimensions to be aggregated can

entail serious problems when aggregating without

any care. In this paper, we propose a methodology to

build finite partial valuation scales consistently with

WAM aggregation.

The paper is organized as follows. Some

considerations are given about the way continuous

cardinal scales are constructed with the Escota

operating domain experts. Then, it is explained how

to build a WAM aggregation operator w.r.t. each

operating domain, in order to be consistent with the

identified scales. The MACBETH method is the

support of these first two steps. The problem related

to the finite scales, that the experts use when

assigning partial scores to an operation, is then

considered. A method is proposed to ensure a

logically sound interface between symbolic

assessments and numerical computations in the

framework of WAM aggregation. Then, a robustness

analysis is proposed to determine the potential

causes of overestimation or underestimation in the

evaluation process of an operation.

2 CARDINAL SCALES OF

EMERGENCY DEGREES

2.1 Nature of Scales

The purpose of this section is to explain how we

have worked with Escota experts of the different

operating domains in order to properly identify their

emergency scales. There are one emergency scale

for each criterion of the domain and one scale for the

aggregated emergency value. In the following we

will consider the case of the operating domain

“carriageway”. Eight criteria (n=8) are related to it:

security, durability, regulation, comfort, public

image, environment protection, sanitary and social

aspects.

It has been checked a priori that Escota

emergency scales are of cardinal nature: the

emergency scale relative to any of the criteria is an

interval scale.

Let us consider a finite set X. When the elements of

X can be ranked w.r.t. to their attractiveness, this is

ordinal information. It means that a number n(x) can

be associated to any element x of X such that:

A MULTI CRITERIA EVALUATION OVER A FINITE SCALE FOR MAINTENANCE ACTIVITIES OF A

MOTORWAY OPERATOR

Figure 1: MACBETH - Pair to pair comparison of operations and cardinal scale for security criterion.

,:[ ()()]

yXxy nx ny∀∈ Ρ⇔ f (1)

,:[ ()()]

yXxy nx ny∀∈ Ι⇔ =

(2)

where relation P « is more attractive than » is

asymmetric and non transitive and relation I « is as

attractive as » is an equivalence relation. n(x)

defines an ordinal scale.

Based upon this first level of information, an

interval scale can then be built. The next step

consists in evaluating the difference of intensity of

preference between elements of X. It implies the

following constraints:

∈=− kkynxn ,)()(

(3)

where k characterizes the intensity of preference

and

enables to respect the limits of the domain

(for example [0,1]). The resolution of a system of

equations of type (1), (2) and (3) provides an

interval scale. That’s the principle used in the

MACBETH method (Bana e Costa, 1994).

2.2 Emergency Scales and MACBETH

Method

The problem of commensurability of the dimensions

to be aggregated is at the heart of the MACBETH

method. Aggregation can be envisaged only if the

scales relative to the emergency criteria are

commensurable (Clivillé, 2004). Then, MACBETH

guarantees the consistency between the resulting

partial scales and the WAM aggregation (Bana e

Costa, 1994).

First, a training set of operations is constituted.

A ranking of the operations in terms of emergency is

established w.r.t. each criterion. At this stage,

information is purely ordinal. Then, for each

criterion, the solutions are compared pair to pair.

Two fictive alternatives are introduced in the

comparison process; they provide the reference

values corresponding to the two emergency degrees:

zero and one. The zero (resp. one) emergency degree

corresponds to the threshold value under which

operations are considered as not urgent at all (resp.

highly urgent). The comparison then consists in

quantifying the difference of emergency degree for

each criterion. This difference is expressed in a finite

set of labels: for example, “equivalent”, “weak”,

“strong” and “extreme”. The resulting set of

constraints defines a linear programming problem.

The solution of this problem provides the cardinal

scale of emergency associated to one criterion. This

step is repeated for each criterion.

Figure 1 illustrates this process for criterion

security. The carriageway expert compares 10

operations {A… J} pair to pair. The real names of

operations are not given for confidentiality reasons.

Two fictive operations urgent (highly urgent) and

peu_urgent (not urgent at all) complete the training

base. The “positive” label in figure 1 introduces a

more flexible constraint because it simply replaces

any label with a higher degree than weak. The

resulting cardinal scale is given at the right side of

Figure 1.

Finally, this procedure is then applied to identify the

weights of the WAM operator. The pair to pair

comparison is carried out over the eight criteria of

the carriageway domain (Figure 2). The resulting

interval scale of weights is given in Figure 2. Let us

note the weights

1..in=

(n=8 for the

carriageway domain). At this stage of the modelling,

the carriageway expert has identified his 8

emergency scales and his WAM parameters. He is

supposed to be able to compute the global degree of

emergency of any operation when partial quotations

are available, w.r.t. each criterion:

() .

WAM OP p u

∑

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

Figure 2: MACBETH - Pair to pair comparison of carriageway criteria and weights identification.

3 DISCRETE CARDINAL

SCALES OF EMERGENCY

Partial scores aggregation does not cause any

problem when quotations referred to continuous

cardinal scales. As explained in section 1, it is more

questionable when partial scores are expressed on a

discrete or finite scale. Indeed, Escota experts

express their assessment w.r.t. each criterion on a

finite set of 3 labels

123

{, , }UUU . The different U

define a discrete cardinal scale. However, computing

the WAM value necessitates assigning numerical

values to each U

. In the following, we describe the

way this assignment can be achieved in a consistent

manner with previous MACBETH identification

phases.

A continuous cardinal scale has been identified

with MACBETH method for the emergency scale of

each criterion. The problem is now to assign a set of

numerical values

{

}

iii

uuu

321

,, to

123

{, , }UUU

for

criterion i. Let us suppose the continuous cardinal

scale for criterion i has been identified with a

training set of q operations. These operations are

grouped into 3 clusters corresponding to

123

,,UUU

The computation of the clusters and their associated

centres is achieved by minimizing the quadratic

difference

(())

uuOP

−

∑∑

where

q is the

number of operations in class

U (

∑

) and

()

uOP

, j=1..q, the emergency degree of an

operation

computed with MACBETH

(Figure 1).

In the example of Figure 1, the computation of

clusters gives:

sec

0.91

urity

u =

sec

0.52

urity

u =

and

sec

0.11

urity

u = .

This assignment is repeated for each criterion

relative to the carriageway domain. Then, the WAM

can be numerically computed:

• For each criterion i , 1..in= ( 8n = ), a value

U is affected to an operation OP. Let us note this

emergency degree

()ki

U ;

•

is thus described by its vector of

emergency degrees

(1) ( )

[,.., ]

kkn

UU;

• The corresponding vector of numerical

values is:

(1) ( 2) ( )

{ , ,.., }

kk kn

uu u

;

()

() .

iki

WAM OP p u

∑

(4)

The last constraint to be satisfied is that the

WAM values must be converted in return into the

semantic universe

123

{, , }UUU . The output of the

WAM operator must be discretized in

123

{, , }UUU .

The problem is thus to determine the centres of the

U clusters of the aggregated emergency scale

(WAM values).

Let us note that the WAM operator is idempotent.

Therefore, we must have:

, {1, 2, 3}, ( , ..., )

kkkk

Uk WAMU U U

∀

∈= (5)

A MULTI CRITERIA EVALUATION OVER A FINITE SCALE FOR MAINTENANCE ACTIVITIES OF A

MOTORWAY OPERATOR

A sufficient condition for (5) is that the centres

of the

U clusters of the aggregated emergency

scale are the images of the corresponding

centres of the partial emergency scales by the WAM

function, i.e.:

( ,.., ) .

niAg

kk ikk

WAM u u p u u

∑

(6)

where

u is the centre of class

U in the

aggregated emergency scale.

Consequently, when an operation is defined by

its partial emergency vector

(1) ( )

[ ,.., ]

kkn

UU,

equation (4) provides the numerical value

()

() .

iki

WAM OP p u

∑

(7)

Then, the attribution of a class

U in the

aggregated emergency scale is obtained through the

following calculation:

()

min .

Ag i

kiki

upu

−

∑

(8)

The value of k in

{1, 2 , 3}

that minimizes the

expression in (8) provides the class

U of operation

OP.

Figure 3 summarizes the whole evaluation

process of an operation OP. The validation of this

process has been carried out with a test base of 23

operations in the carriageway domain. The

carriageway expert has analysed each of these

operations. For each of them, he has attributed

emergency degrees in the Escota normalized

semantic universe

123

{, , }UUU w.r.t. every of his

8 criteria.

Then, the aggregated emergency degree in this

semantic universe can be computed using the 3-step

process described in this paper (white arrows in

Figure 3). Besides these computations, the expert

has been asked to directly attribute an overall

emergency degree to each of the 23 operations (grey

arrow in Figure 3).

Figure 3: Evaluation process of an operation.

Figure 4 reports these data. The last line

corresponds to the direct expert evaluation (grey

arrow). The last but one line provides the

corresponding computed values with the 3-step

method (white arrows). No error has been observed.

However, the poor semantic universe—only 3

labels—implied in our application can also partly

explain such a perfect matching.

Figure 4: Tests on the evaluation method over a base of 23 operations

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

4 THE MC HIERARCHICAL

EVALUATION BY ESCOTA

In this paper, the study was focused on the MC

evaluation by the expert of an operating domain.

However, as evocated in section 1, planning of

operations, by Escota, is more complex. The

emergency assessment by operating domain experts

described here is only part of a hierarchical MC

evaluation process. From symptoms detection on

elements of infrastructure to operation planning, a

similar MC evaluation is carried out at different

functional levels in the Escota organization.

The complete information processing used for

Escota preventive maintenance can be formalized as

the following sequence of risk analysis. Periodic

inspections are performed to detect and measure any

malfunction symptoms as early as possible. The

expert in charge of a domain then analyses these

technical diagnoses and evaluates the situation

seriousness. The official in charge of the operating

network coordinates and ponders the experts’ needs

and demands. Each actor of this information

processing system participates to a tripartite MC

decision-making logic: measurement, evaluation and

decision. To each step of this process corresponds a

specific set of criteria and an aggregation operator:

seriousness of a malfunction results from a

prescribed aggregation of the symptoms quotation;

the expert’s interpretation of the diagnosis associates

an emergency degree to the corresponding

maintenance operation w.r.t. the criteria relating to

his operating domain (technical risks assessment);

finally, the manager attributes a priority degree to

the operation on the basis of a set of more strategic

criteria (strategic risks analysis).

This hierarchical MC evaluation process enables

to breakdown the decision-making into elementary

steps. Each step collaborates to the enrichment of

information from measures to priority degrees and

thus contributes to the final step, i.e. operation

planning.

We have developed a dynamic Information

Processing System (IPS) to support this hierarchical

MC evaluation of the infrastructure condition and

facilitate the way decision-makers use their

reasoning capabilities through adequate information

processing procedure.

Figure 5 illustrates the man machine-interface

the expert has at his disposal to fulfil an emergency

form relative to an operation. Finally, the emergency

evaluation synthesis (Figure 6) can be consulted by

the official in charge of the operation network before

he proceeds to his own MC evaluation.

Figure 5: Keyboarding of an emergency form.

Figure 6: Emergency evaluation synthesis.

5 THE ROBUSTNESS ANALYSIS

OF THE EVALUATION

PROCESS

Let us now consider a last step in the evaluation

process: assessment of the risk of erroneous

estimation w.r.t. the emergency of an operation, i.e.,

the risk of underestimation or overestimation of the

aggregated emergency score of an operation. It relies

on a robustness analysis of the evaluation procedure

based upon the WAM. Two aims are assigned to this

step, it must answer the following questions: 1)

when an erroneous partial estimation is done w.r.t.

criterion i, what is the risk the aggregated emergency

degree to be affected? 2) when an operation appears

to be underestimated (resp. overestimated), which

criteria could most likely explain this faulty result?

The first question corresponds to an a priori risk

estimation of erroneous evaluation; the second

question is related to a diagnosis analysis.

Let us first define the notion of neighbourhood of

a vector of emergency degrees

(1) ( )

[ ,.., ]

kkn

associated to an operation OP. The vectors of the

neighbourhood of

(1) ( )

[ ,.., ]

kkn

are all the vectors

(1) ( )

[ ,.., ]

kkn

such that:

() ()

{1 . . } ,

ki ki

inUU∀∈ =

()ki

is the value just above (resp. below)

()ki

(when

A MULTI CRITERIA EVALUATION OVER A FINITE SCALE FOR MAINTENANCE ACTIVITIES OF A

MOTORWAY OPERATOR

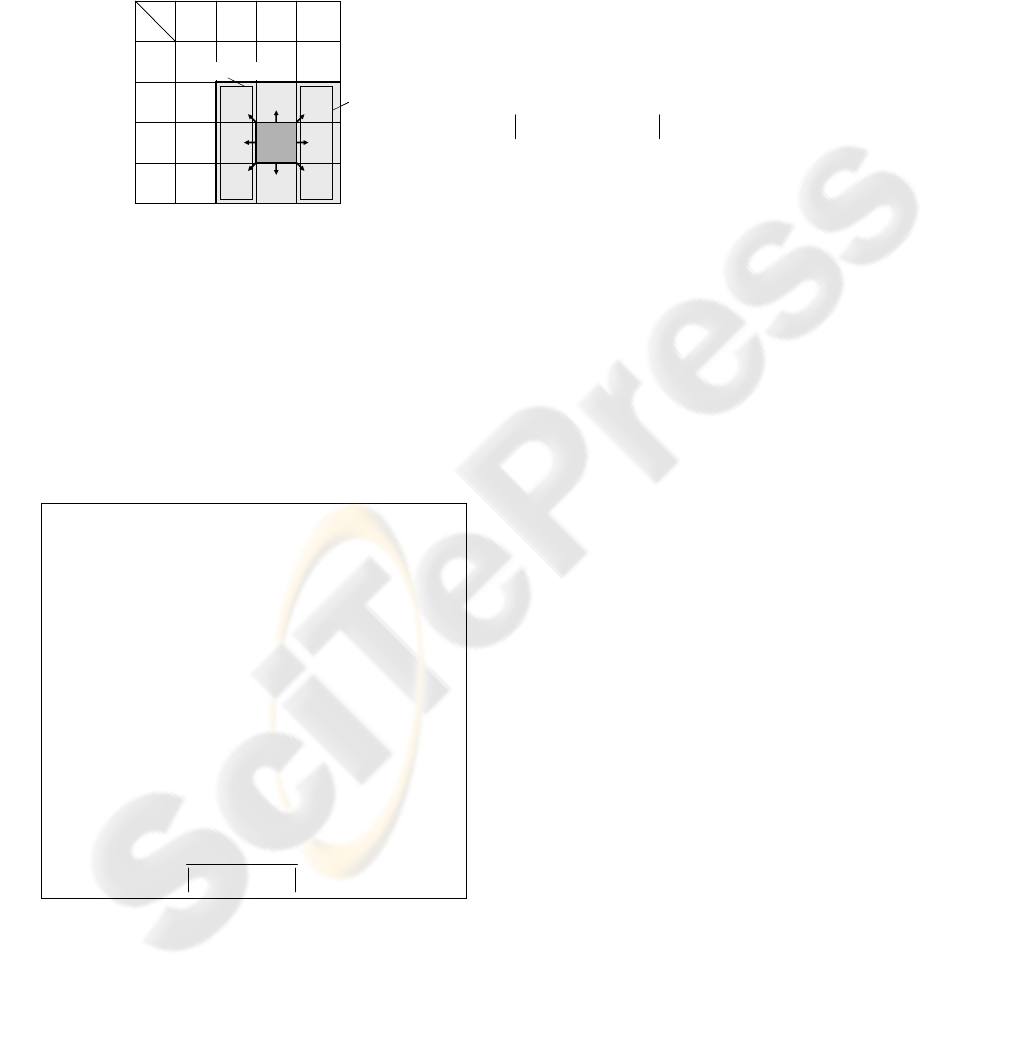
defined; indeed, there is no value below zero and no

value above

). The neighbourhood is a set of

vectors denoted

(1) ( )

([ ,.., ])

kkn

UUΝ

. In the example in

dimension 2 in Figure 8,

(1) 2k

UU=

and

(2) 2k

The values of component

(12)ior=

of a neighbour

vector may be

. There are 8

neighbours. In the general case, the maximal number

of neighbours is

− .

Figure 7: Neighbourhood of the vector of emergency

degrees (U

, U

) in dimension 2.

5.1 Risk of Erroneous Estimation

The risk of misclassification of an operation due to

an overestimation (resp. underestimation) w.r.t. a

criterion

i enables the expert in charge of a domain

to assess the impact of an evaluation error w.r.t.

criterion

i on the overall emergency degree of the

operation. The higher, the more carefully the partial

appraisal w.r.t. criterion

i must be carried out.

Compute

()WAM U

For each criterion i :

• Find all the vectors

(1) ( )

' [ ,.., ]

kkn

UU U=

()UΝ

such that

()ki

takes the value just above

()ki

(when defined, else

() 1ki

UU=

and there is no risk of

underestimation w.r.t. criterion i in this case). Note this

set:

()Under i U

• Count the numbers of vectors

()Under i U

such that

(')WAM U

is higher than

()WAM U

. Note this number

_under i

• The risk of underestimation induced by

criterion i for an operation characterized by

is then:

_()

()

under i

risk under i

Under i U

The lower, the weaker the impact of the criterion to

the global emergency degree. The risk analysis is

based upon the following algorithm. We’ll first

consider the risk of underestimation for sake of

simplicity. We consider that a value

()ki

underestimated (resp. overestimated) when it should

take the value just above

()ki

(resp. just

below

()ki

). This assumption means that the worst

appraisal error w.r.t. one criterion can only

correspond to the value just below or just above for

this criterion.

Let’s consider a vector

(1) ( )

[,.., ]

kkn

UU U

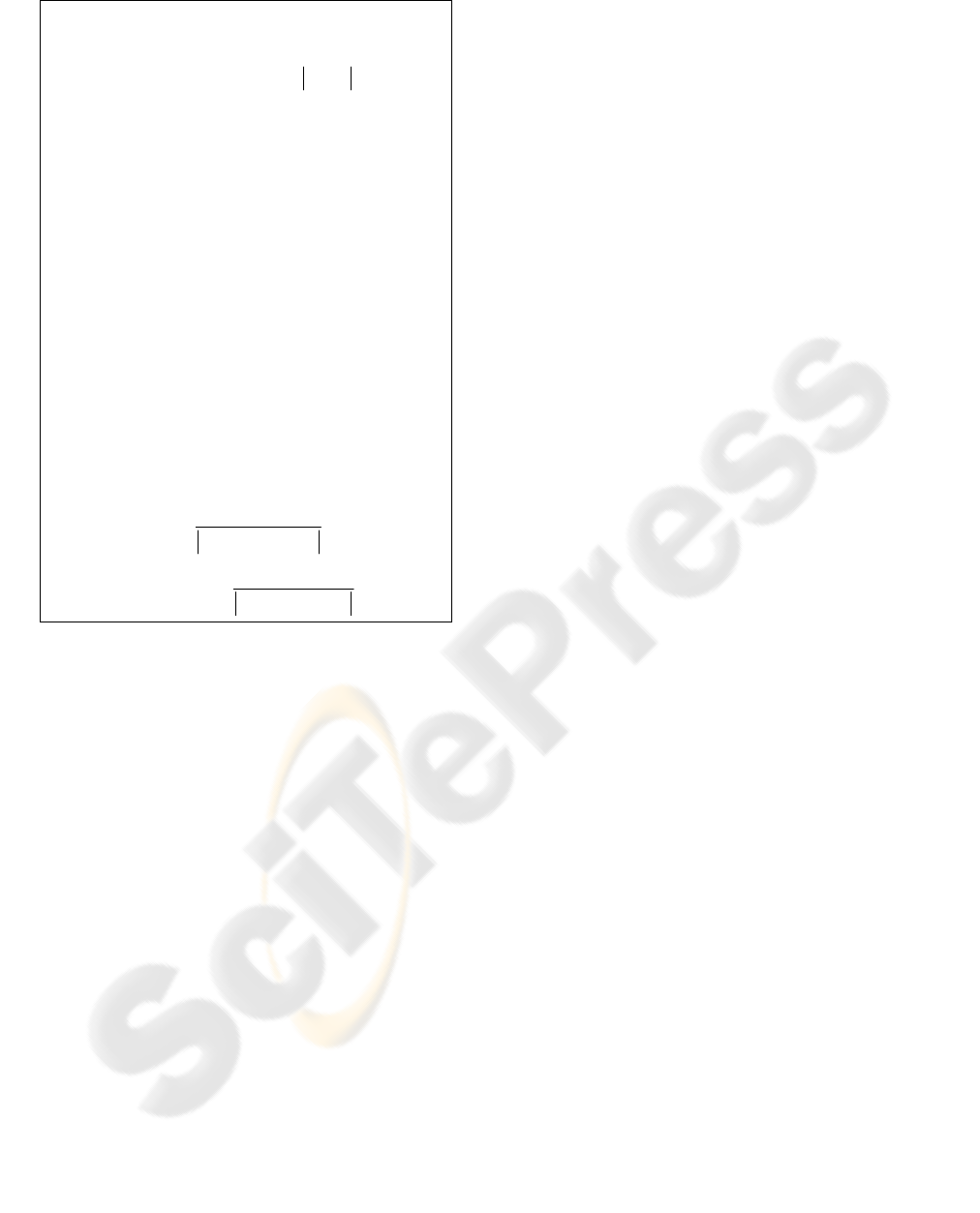
In the example in Figure 8, let us consider an

assumption of underestimation w.r.t. criterion 1. The

set

1( , )Under U U

is represented in the figure.

1( , ) 3Under U U

; only

(, )UU

and

(, )UU

lead to an overall underestimation (the operation is

evaluated

whereas it should be

). Then,

under

and

(1) 2 / 3risk under =

. It means that

an underestimation w.r.t. criterion 1 for an operation

characterized by

(, )UU

leads to an

underestimation of the overall degree of emergency

of the operation in 66% of the cases.

The algorithm is the same for the risk of

overestimation. Nevertheless, in this case, when

()

, the risk of overestimation w.r.t. criterion i

is null. Figure 9 and Figure 10 provide the results for

the risk analysis when underestimation (Figure 9)

and when overestimation (Figure 10) for all the

vectors in Figure 4.

5.2 Diagnosis Analysis

When the degree of emergency of an operation is

suspected to be overestimated (resp.

underestimated), the diagnosis analysis consists in

determining the most likely causes, i.e., the criteria

that the most frequently entail an overestimation

(resp. underestimation) of the operation when

they’re overestimated (resp. underestimated)

themselves. The possibility that criterion

i is a cause

of overestimation (resp. underestimation) assuming

an overestimation (resp. underestimation) of the

overall emergency degree of the operation― is

computed in the diagnosis step.

Let us consider the algorithm in case of

underestimation (resp. overestimation).

()Diag under i

gives the rate that an

underestimation w.r.t. criterion

i be a potential cause

of underestimation of the overall emergency degree

of an operation (idem for overestimation).

Criterion 1

Criterion 2

_1( , )Under U U

_1( , )Over U U

Criterion 1

Criterion 2

_1( , )Under U U

_1( , )Over U U

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

Let’s consider a vector

(1) ( )

[,.., ]

kkn

UU U=

Compute

()

WAM U

Compute

()

UΝ

and its cardinal

()UΝ

• Compute

(')

WAM U

for each

(1) ( )

' [ ,.., ]

kkn

UU U=

()UΝ

• Let us note

()

igher UΝ

(resp.

()Lower UΝ

), the set of vectors

()UΝ

such that

(') ()

WAM U WAM U>

(resp.

(') ()WAM U WAM U<

)

• For each criterion i, count the number

_under i

n (resp.

_over i

n ) of times criterion i is

underestimated (resp. overestimated) in a vector

()

igher UΝ

(resp.

()Lower UΝ

), i.e.,

()ki

takes the value just above

()ki

(resp. just

below

()ki

) in

()

igher UΝ

(resp.

()Lower UΝ

)

Compute for each criterion i:

_()

()

under i

Diag under i

igher U

(resp.

_()

()

over i

Diag over i

Lower U

)

Figure 11 concerns underestimation diagnosis

and Figure 12 overestimation diagnosis for the base

of operations in Figure 4. A rate indicates the

possibility a criterion is underestimated itself (resp.

overestimated) when the overall emergency degree

of the concerned operation is underestimated (resp.

overestimated).

6 CONCLUSION

In civil engineering, the culture of numbers is

strongly developed. People commonly manipulate

symbolic labels but attribute them numerical values

when necessary without further care. A typical case

is when aggregation procedures are required. We

have proposed a methodology that enables 1) experts

to express their judgement values in their own

discrete semantic universe, 2) to convert the labels in

adequate numerical values using the MACBETH

method and clustering techniques, 3) to compute the

WAM based aggregated value and convert it in

return into the experts’ semantic universe 4) to carry

out a robustness analysis of the evaluation process to

assess the risk of misclassification of the operations

and to diagnose these misclassifications. This

method is implemented in an IPS—SINERGIE—

that supports decisions concerning maintenance

operations planning by the motorway operator

Escota.

REFERENCES

Saaty, T.L. 1980. The Analytic Hierarchy Process.

McGraw-Hill , New York.

Bana e Costa, C.A., Vansnick, J.C., 1994. MACBETH -

an interactive path towards the construction of cardinal

value functions. International transactions in

Operational Research, 1, 489-500.

Clivillé, V., 2004. Approche Systémique et méthode

multicritère pour la définition d’un système

d’indicateurs de performance. Thèse de l’Université de

Savoie, Annecy.

Jullien, S., Mauris, G., Valet, L., Bolon, Ph., 2006.

Decision aiding tools for Animated film selection from

a mean aggregation of criteria preferences over a finite

scale. 11th Int. Conference on Information processing

and Management of uncertainty in Knowledge-Based

Systems, Paris, France.

Grabisch, M., 2006. Representation of preferences over a

finite scale by a mean operator. To appear in

mathematical Social Sciences, downloadable at www-

sysdef.lip6.fr/~grabisch.

A MULTI CRITERIA EVALUATION OVER A FINITE SCALE FOR MAINTENANCE ACTIVITIES OF A

MOTORWAY OPERATOR

Figures 8 and 9: risk of overall underestimation (resp. overestimation) of the operations induced by partial underestimations

(resp. overestimation) w.r.t. criteria.

Figures 10 and 11: rates of causes of underestimation (resp. overestimation) diagnoses.

1721193012112915142728136987252423225218

env 11.0% 44.0% 0% 0% 15.0% 2.0% 0% 0% 0% 26.0% 13.0% 41.0% 0% 0% 0% 0% 18.0% 21.0% 0% 0% 0% 0% 21.0%

sanitary 11.0% 42.0% 0% 0% 14.0% 1.0% 0% 0% 0% 26.0% 13.0% 39.0% 0% 0% 0% 0% 18.0% 21.0% 0% 0% 0% 0% 21.0%

comfort 25.0% 58.0% 0% 0% 25.0% 4.0% 0% 0% 0% 40.0% 27.0% 55.0% 0% 0% 0% 0% 28.0% 32.0% 0% 0% 0% 0% 37.0%

regulation 11.0% 45.0% 0% 0% 16.0% 2.0% 0% 0% 0% 34.0% 20.0% 43.0% 0% 0% 0% 0% 20.0% 25.0% 0% 0% 0% 0% 23.0%

security 32.0% 67.0% 0% 0% 37.0% 4.0% 0% 0% 0% 62.0% 35.0% 76.0% 0% 0% 0% 0% 41.0% 46.0% 0% 0% 0% 0% 55.0%

durability 15.0% 73.0% 0% 0% 28.0% 4.0% 0% 0% 0% 32.0% 17.0% 62.0% 0% 0% 0% 0% 39.0% 44.0% 0% 0% 0% 0% 27.0%

social 11.0% 42.0% 0% 0% 14.0% 1.0% 0% 0% 0% 26.0% 13.0% 39.0% 0% 0% 0% 0% 18.0% 21.0% 0% 0% 0% 0% 21.0%

public image 18.0% 56.0% 0% 0% 26.0% 4.0% 0% 0% 0% 44.0% 27.0% 58.0% 0% 0% 0% 0% 29.0% 34.0% 0% 0% 0% 0% 39.0%

1721193012112915142728136987252423225218

env 2.0% 3.0% 0.0% 53.0% 7.0% 30.0% 12.0% 17.0% 17.0% 1.0% 6.0% 0.0% 41.0% 34.0% 34.0% 28.0% 13.0% 11.0% 6.0% 6.0% 0.0% 0.0% 1.0%

sanitary 2.0% 3.0% 0.0% 53.0% 6.0% 29.0% 12.0% 16.0% 16.0% 1.0% 6.0% 0.0% 34.0% 34.0% 34.0% 22.0% 13.0% 11.0% 6.0% 6.0% 0.0% 0.0% 1.0%

comfort 8.0% 7.0% 1.0% 69.0% 13.0% 46.0% 19.0% 24.0% 24.0% 3.0% 14.0% 2.0% 51.0% 51.0% 51.0% 39.0% 20.0% 18.0% 12.0% 12.0% 2.0% 1.0% 3.0%

regulation 3.0% 3.0% 1.0% 58.0% 9.0% 32.0% 19.0% 23.0% 23.0% 1.0% 6.0% 1.0% 40.0% 35.0% 35.0% 28.0% 14.0% 14.0% 7.0% 7.0% 1.0% 0.0% 1.0%

security 8.0% 9.0% 1.0% 72.0% 18.0% 63.0% 35.0% 47.0% 47.0% 3.0% 18.0% 2.0% 74.0% 80.0% 80.0% 56.0% 30.0% 27.0% 19.0% 19.0% 2.0% 1.0% 3.0%

durability 8.0% 9.0% 1.0% 96.0% 17.0% 49.0% 24.0% 30.0% 30.0% 3.0% 11.0% 2.0% 48.0% 48.0% 48.0% 36.0% 39.0% 34.0% 18.0% 18.0% 2.0% 1.0% 3.0%

social 2.0% 3.0% 0.0% 53.0% 6.0% 29.0% 12.0% 16.0% 16.0% 1.0% 6.0% 0.0% 34.0% 34.0% 34.0% 22.0% 13.0% 11.0% 6.0% 6.0% 0.0% 0.0% 1.0%

public image 3.0% 5.0% 1.0% 60.0% 15.0% 44.0% 24.0% 29.0% 29.0% 3.0% 14.0% 2.0% 53.0% 48.0% 48.0% 33.0% 20.0% 18.0% 12.0% 12.0% 2.0% 1.0% 3.0%

1721193012112915142728136987252423225218

durability 45% 57% 0% 0% 67% 100% 0% 0% 0% 40% 42% 52% 0% 0% 0% 0% 71% 67% 0% 0% 0% 0% 41%

security 97% 53% 0% 0% 86% 100% 0% 0% 0% 79% 87% 64% 0% 0% 0% 0% 75% 71% 0% 0% 0% 0% 84%

comfort 77% 45% 0% 0% 59% 90% 0% 0% 0% 51% 66% 46% 0% 0% 0% 0% 51% 49% 0% 0% 0% 0% 56%

public image 55% 44% 0% 0% 62% 90% 0% 0% 0% 56% 66% 48% 0% 0% 0% 0% 53% 52% 0% 0% 0% 0% 60%

env 35% 35% 0% 0% 36% 45% 0% 0% 0% 33% 33% 35% 0% 0% 0% 0% 33% 33% 0% 0% 0% 0% 33%

regulation 35% 35% 0% 0% 37% 45% 0% 0% 0% 43% 51% 36% 0% 0% 0% 0% 37% 39% 0% 0% 0% 0% 35%

social 33% 33% 0% 0% 33% 33% 0% 0% 0% 33% 33% 33% 0% 0% 0% 0% 33% 33% 0% 0% 0% 0% 33%

sanitary 33% 33% 0% 0% 33% 33% 0% 0% 0% 33% 33% 33% 0% 0% 0% 0% 33% 33% 0% 0% 0% 0% 33%

1721193012112915142728136987252423225218

durability 100% 100% 100% 60% 82% 57% 66% 61% 61% 100% 60% 100% 46% 46% 46% 53% 94% 96% 93% 93% 100% 100% 100%

security 100% 100% 100% 46% 90% 72% 96% 95% 95% 100% 100% 100% 71% 78% 78% 84% 73% 75% 100% 100% 100% 100% 100%

comfort 100% 78% 100% 44% 66% 53% 53% 48% 48% 100% 80% 100% 50% 50% 50% 57% 50% 51% 62% 62% 100% 100% 100%

public image 45% 60% 100% 38% 74% 50% 66% 58% 58% 100% 80% 100% 51% 46% 46% 50% 50% 51% 62% 62% 100% 100% 100%

env 35% 34% 33% 33% 35% 34% 33% 35% 35% 33% 33% 40% 40% 33% 33% 42% 33% 33% 33% 33% 33% 50% 33%

regulation 40% 39% 100% 35% 43% 36% 53% 46% 46% 33% 33% 60% 39% 34% 34% 42% 35% 41% 37% 37% 50% 50% 33%

social 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33%

sanitary 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33% 33%

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics