
USING NOISE TO IMPROVE MEASUREMENT AND
INFORMATION PROCESSING
Solenna Blanchard, David Rousseau and Franc¸ois Chapeau-Blondeau
Laboratoire d’Ing
´
enierie des Syst
`
emes Automatis
´
es (LISA), Universit
´
e d’Angers
62 avenue Notre Dame du Lac, 49000 Angers, France
Keywords:
Noise, Stochastic resonance, Information processing, Measurement, Sensor.
Abstract:
This paper proposes a synthetic presentation on the phenomenon of stochastic resonance or improvement
through the action of noise. Several situations and mechanisms are reported, demonstrating a constructive
role of noise, in the context of measurement and sensors, data and information processing, with examples on
digital images.
1 INTRODUCTION
In the context of measurement and information pro-
cessing, it is progressively realized that noise is not al-
ways a nuisance, but that it can sometimes play a ben-
eficial role (Wiesenfeld and Moss, 1995; And
`
o and
Graziani, 2001; Chapeau-Blondeau and Rousseau,
2002; Chapeau-Blondeau and Rousseau, 2004). Such
a constructive role of noise can be observed in diverse
situations, through different cooperative mechanisms,
assessed by various measures of performance to quan-
tify the improvement. The term “stochastic reso-
nance” is used as a common name to unify these sit-
uations where a measure of performance is improved
to culminate (resonate) at a maximum when the level
of noise is raised. In the recent years, many forms of
stochastic resonance have been introduced and ana-
lyzed. Experimental observations of stochastic reso-
nance have been obtained in many areas, for instance
with electronic circuits, optical devices, neuronal pro-
cesses, nanotechnologies.
In the present paper, we propose an overview of
some basic mechanisms of stochastic resonance, in-
cluding some recent ones, that we organize in a syn-
thetic perspective. We specially focus on possible
constructive role of noise for measurement and sen-
sors, data and information processing. For illus-
tration, we provide examples on digital images, a
class of signals not so often considered for applying
stochastic resonance, which gives us the opportunity
of also showing new examples.
2 NOISE-SHAPED SENSORS
In this section, we show a constructive action of the
noise that can be used to shape the input–output char-
acteristic of devices and we give an example of appli-
cation illustrated with saturating imaging sensors.
We consider a device with static nonlinear input–
output characteristic g(·). This device is in charge of
the transmission or the processing of an information
carrying signal s so as to produce the output signal y
with
y = g(s) , (1)
where input signal s and output signal y may be func-
tion of time or space. Let us assume that the input–
output characteristic g(·) of our device is not opti-
mally adapted to transmit or process the input sig-
nal s. Therefrom, one may look for another de-
vice with a more suitable input–output characteristic
shape. As an alternative, we are going to show that it
is also sometimes possible to modify the input–output
characteristic g(·) of such a device without having to
change any physical parameter of the device itself.
We introduce a noise η in the input–output rela-
tion of Eq. (1) which becomes y = g(s + η). This
noise η can be a native noise due to the physics of the
device or a noise purposely injected to the input of the
device. Then, since the device is no longer determin-
istic, an effective or average input–output characteris-
tic can be defined as g
eff
(·) given by the expectation
g
eff
(s) = E[y] =
+∞
−∞
g(u) f
η
(u− s)du , (2)
268
Blanchard S., Rousseau D. and Chapeau-Blondeau F. (2007).
USING NOISE TO IMPROVE MEASUREMENT AND INFORMATION PROCESSING.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 268-271
DOI: 10.5220/0001621502680271
Copyright
c
SciTePress
with f
η
(u) the probability density function of the
noise η. In presence of the noise η, the shape of the
device input–output characteristic, g
eff
(·) in Eq. (2),
is now controlled by g(·) and by the noise probability
density function f
η
(u). Therefore, a modification in
the response of a memoryless device can be obtained
thanks to the presence of a noise η which makes it
possible to shape the input–output characteristic of
the device without changing the device itself.
In practice, the modified input–output characteris-
tic g
eff
(·) of the device in Eq. (2) is not directly avail-
able. Yet, it is possible to have a device presenting an
approximation of the response of Eq. (2) by averaging
N acquisitions y
i
with i ∈ {1,...N} to produce
y =
1
N
N
∑
i=1
y
i
=
1
N
N
∑
i=1
g(s+ η
i
) , (3)
where the N noises η
i
are white, mutually indepen-
dent and identically distributed with probability den-
sity function f
η
(u). Practical implementation of the
process of Eq. (3) can be obtained, as proposed in
(Stocks, 2000) for 1-bit quantizers, via replication of
the devices associated in a parallel array where N in-
dependent noises are added at the input of each de-
vice or, as proposed in (Gammaitoni, 1995) for a con-
stant signal, by collecting the output of a single device
at N distinct instants. Similarly to what is found in
Eq. (2), the input–output characteristic of the process
of Eq. (3) is shaped by the presence of the N noises
η
i
. Because of Eq. (3), one has first
E[y] = E[y
i
] , (4)
and also one has for any i
E[y
i
] =
+∞
−∞
g(s+ u) f
η
(u)du . (5)
The N noises η
i
bring fluctuations which can be quan-
tified by the nonstationary variance var[y] = E[y
2
] −
E[y]
2
, with E[y
2
] = E[y
2
i
]/N + E[y]
2
(N − 1)/N and
E[y
2
i
] =
+∞
−∞
g
2
(s+ u) f
η
(u)du . (6)
For large values of N, var[y] tends to zero. In these
asymptotic conditions where N tends to infinity, the
process constituted by the device g(·), the N noises η
i
and the averaging of Eq. (3), becomes a determinis-
tic equivalent device with input–output characteristic
given by Eq. (2). For finite values of N, the presence
of N noises η
i
will play a constructive role if the im-
provement brought to the transmission or processing
of the input signal s by the modification of the device
characteristic is greater than the nuisance due to the
remaining fluctuations in y.
The process of Eq. (3) delimits a general prob-
lem: given a device characteristic g(·) and a num-
ber N of averaging samples, how can one choose the
probability density function of the noises η
i
to ob-
tain a targeted characteristic response. This inverse
problem is, in general, difficult to solve. A pragmatic
solution, inspired from the studies on stochastic reso-
nance, consists in fixing a probability density function
for the noises η
i
and to act only on the rms amplitude
σ
η
of these identical independent noises.
For illustration, we now give an example of appli-
cation of the process of Eq. (3). We consider devices
with input–output characteristic g(u) presenting a lin-
ear regime limited by a threshold and a saturation
g(u) =
0 pour u ≤ 0
u pour 0 < u < 1
1 pour u ≥ 1 .
(7)
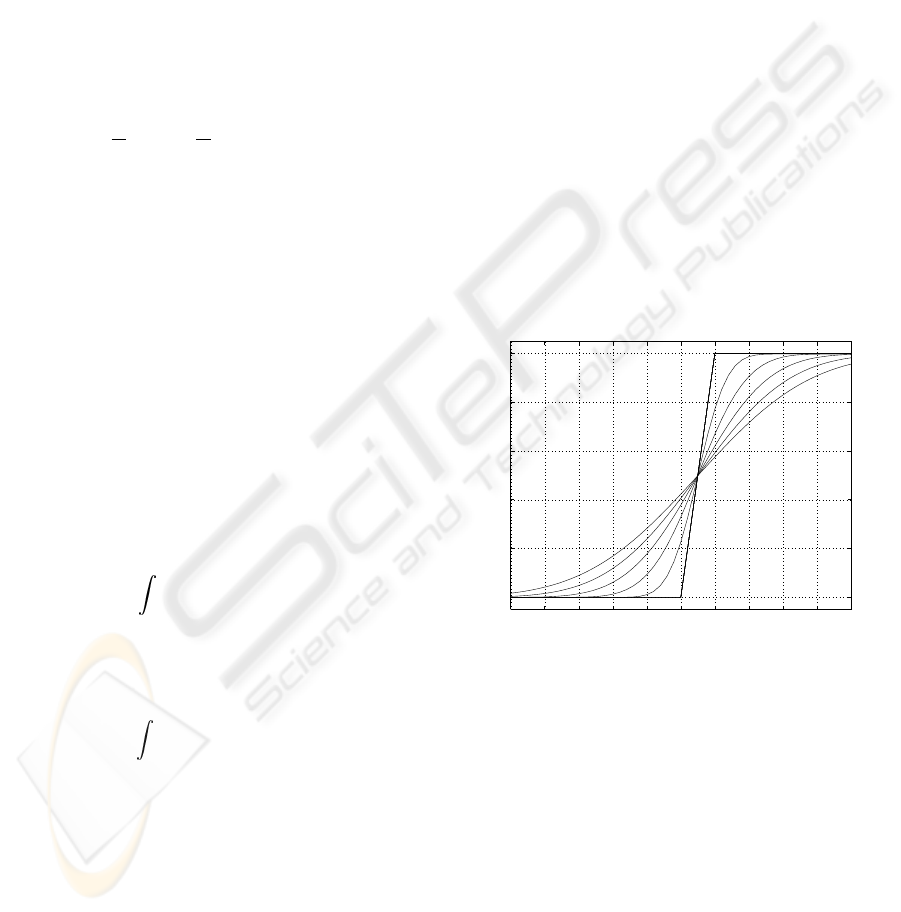
The possibility of shaping the response of such de-
vices by using the process of Eq. (3) is shown in Fig-
ure 1. The noises η
i
injected in Eq. (3), arbitrarily
chosen Gaussian here, tend to extend the amplitude
range upon which the effective input–output charac-
teristic g
eff
(·) of Eq. (2) is linear.
−5 −4 −3 −2 −1 0 1 2 3 4 5
0
0.2
0.4
0.6
0.8
1
input amplitude u
effective characteristic g
eff
(u)
σ
η
=0
σ
η
=2.5
Figure 1: Effective input–output characteristic g
eff
(·) of
Eq. (2) for the device of Eq. (7) in presence of Gaus-
sian centered noise with various rms amplitude σ
η
=
0,0.5,1,1.5, 2.5.
The input–output characteristic g(u) of Eq. (7) can
constitute a basic model for measurement sensors. In
the domain of instrumentation and measurement, a
quasi-linear behavior associated to perfect reconstruc-
tion is sought. Nevertheless, sensor devices are usu-
ally linear for moderate inputs but can present satura-
tion at large inputs or/and a threshold for small inputs.
Such behaviors at large and small inputs induce dis-
tortions degrading the quality of the signal transmitted
by these sensor devices. Therefore, the linear regime
of the input–output characteristic of a saturating sen-
sor usually sets the limit of the signal dynamic to be
USING NOISE TO IMPROVE MEASUREMENT AND INFORMATION PROCESSING
269

transmitted with fidelity. In this measurement frame-
work, the process of Eq. (3) can be used to widen the
dynamic of sensors presenting threshold and satura-
tion like in Eq. (7).
For further illustrations, we consider the case
where Eq. (7) models the response of an imaging sen-
sor (CCD, retina, or even photographic films). We
assume that, although all physical parameters (for ex-
ample luminance of the scene, time exposure, imag-
ing sensor sensibility) have been adjusted to their
best, the image s submitted to Eq. (7) still undergoes
saturation by g(·) and is therefore over-exposed. The
possibility of a noise–widened dynamic of this imag-
ing sensor can be visually appreciated in Figure 2.
Fluctuations due to the presence of noises η
i
in Eq. (3)
are decreasing with increasing N. Nevertheless, in
some cases, as perceptible in Figure 2c, the sensor de-
vice can benefit from the presence of the noise even
with N = 1 in the process of Eq. (3). Also, the noise–
widened visual improvement of the transmitted im-
age, can be quantitatively assessed, in Figure 3, by
the normalized cross-covariance between the original
image and the transmitted image.
3 NOISE-ASSISTED
INFORMATION
TRANSMISSION
We now move to a higher information-processing
level, with statistical quantification of information,
and possible connection to pattern recognition tasks,
for another example of a constructive role of noise.
Consider a binary image with values s(x
1
,x
2
) ∈ {0,1}
at spatial coordinates (x
1
,x
2
). The detector g(·) is
taken as a hard limiter with threshold θ,
g(u) =
0 for u ≤ θ
1 for u > θ ,
(8)
and delivers the output image y(x
1
,x
2
) = g[s(x
1
,x
2
)+
η(x
1
,x
2
)], with independent noise η(x
1
,x
2
) at dis-
tinct pixels (x
1
,,x
2
). When the detection threshold
θ is high relative to the values of the input image
s(x
1
,x
2
), i.e. when θ > 1, then s(x
1
,x
2
) in absence
of the noise η(x
1
,x
2
) remains undetected as the out-
put image y(x
1
,x
2
) remains a dark image; thus, with
no noise, no information is transmitted from s(x
1
,x
2
)
to y(x
1
,x
2
). From this situation, addition of the noise
η(x
1
,x
2
) allows a cooperative effect where s(x
1
,x
2
)
and η(x
1
,x
2
) cooperate to overcome the detection
threshold. This translates into the possibility of in-
creasing and maximizing the information shared be-
tween s(x
1
,x
2
) and y(x
1
,x
2
) thanks to the action of
the noise η(x
1
,x
2
) at a nonzero level which can be
(a) (b)
(c) (d)
(e) (f)
Figure 2: Noise–widened dynamic of an imaging sensor
with response given by Eq. (7). (a) a 8-bit version of the
“lena” image correctly exposed with 256 grey-levels coded
between 0 and 1; (b) over-exposed transmitted image in
absence of noise. The over-exposure is controlled by an
exposure parameter k
ex
, which is a constant added to all
the pixel value of the original image before the process
of Eq. (7); (c) transmitted image with the same exposure
parameter k
ex
= 0.75 but with the presence of zero-mean
Gaussian noise of rms amplitude σ
η
= 0.3 with N = 1
acquisition averaged; (d),(e),(f) same conditions but with
σ
η
= 0.1, 0.2,0.4 with N = 3, 7,63.
optimized. The effect can be precisely quantified by
means of a Shannon mutual information I(s,y) be-
tween s(x
1
,x
2
) and y(x
1
,x
2
), definable as
I(s, y) = H(y) − H(y|s) . (9)
With the function h(u) = −ulog
2
(u), the entropies in
Eq. (9) are
H(y) = h(p
00
p
0
+ p
01
p
1
) + h(p
10
p
0
+ p
11
p
1
) (10)
and
H(y|s) = p
0
[h(p
00
) + h(p
10
)] + p
1
[h(p
01
) + h(p
11
)] .
(11)
In Eqs. (10)–(11) one has the probabilities Pr{s =
1} = p
1
= 1 − p
0
determined by the input image
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
270

0 0.2 0.4 0.6 0.8 1
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
noise rms amplitude
normalized cross−covariance
N=1
N=63
Figure 3: Normalized cross-covariance of original “lena”
image correctly exposed with the image transmitted by the
process of Eq. (3) as a function of the level of the noise σ
η
for various number of acquisitions N = 1,2,3,7, 15, 31,63.
The exposure parameter k
ex
= 0.75 is the same as in Fig-
ure 2.
s(x
1
,x
2
), and
p
0s
= 1− p
1s
= Pr{y = 0|s} = F
η
(θ− s) (12)
determined by the noise η(x
1
,x
2
) via its cumulative
distribution function F
η
(·).
For a 410× 415 binary image with p
1
= 0.3, Fig-
ure 4 shows typical evolutions for information I(s,y)
as a function of the rms amplitude σ
η
of the noise
η(x
1
,x
2
) chosen zero-mean Gaussian. In Figure 4,
when 0 < θ < 1 the noise is felt only as a nuisance,
and information I(s,y) is maximum at zero noise and
decreases when σ
η
grows. Meanwhile, when θ > 1
no information is transmitted in the absence of noise,
and it is the increase of the noise level σ
η
above zero
which authorizes information I(s,y) to grow in or-
der to culminate at a maximum for a nonzero opti-
mal amount of noise maximizing information trans-
mission.
This noise-aided information transmission quan-
tified in Figure 4 can be visually appreciated in Fig-
ure 5, with the optimal noise configuration in the mid-
dle image.
This example illustrates one basic form of noise-
aided information processing, in which the noise has a
constructive influence in a binary decision in the pres-
ence of a fixed discrimination threshold. This basic
form can find applicability in many areas, and can be
elaborated upon in many directions. It can be related
to the effect of dithering known in imaging at low
processing levels (Gammaitoni, 1995). It can also be
related to threshold nonlinearities found in biophysi-
cal sensory processes, for instance originating in the
retina for visual perception (Patel and Kosko, 2005).
At high processing levels, the effect is relevant to pat-
tern recognition in human vision (Piana et al., 2000).
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
noise rms amplitude
mutual information
θ=0.8
θ=1.2
Figure 4: Mutual information I(s, y), as a function of the
noise rms amplitude σ
η
, in succession for the threshold θ =
0.8,0.9,0.95,0.99, 1,1.01,1.05,1.1 and 1.2.
Figure 5: Output image y(x
1
,x
2
) with threshold θ = 1.1 and
noise level σ
η
= 0.05 (left), 0.4 (middle) and 1.3 (right).
REFERENCES
And
`
o, B. and Graziani, S. (2001). Adding noise to improve
measurement. IEEE Instrumentation and Measure-
ment Magazine, 4:24–30.
Chapeau-Blondeau, F. and Rousseau, D. (2002). Noise im-
provements in stochastic resonance: From signal am-
plification to optimal detection. Fluctuation and Noise
Letters, 2:L221–L233.
Chapeau-Blondeau, F. and Rousseau, D. (2004). Noise-
enhanced performance for an optimal Bayesian es-
timator. IEEE Transactions on Signal Processing,
52:1327–1334.
Gammaitoni, L. (1995). Stochastic resonance and the
dithering effect in threshold physical systems. Physi-
cal Review E, 52:4691–4698.
Patel, A. and Kosko, B. (2005). Stochastic resonance in
noisy spiking retinal and sensory neuron models. Neu-
ral Networks, 18:467–478.
Piana, M., Canfora, M., and Riani, M. (2000). Role of noise
in image processing by the human perceptive system.
Physical Review E, 62:1104–1109.
Stocks, N. G. (2000). Suprathreshold stochastic resonance
in multilevel threshold systems. Physical Review Let-
ters, 84:2310–2313.
Wiesenfeld, K. and Moss, F. (1995). Stochastic resonance
and the benefits of noise: From ice ages to crayfish
and SQUIDs. Nature, 373:33–36.
USING NOISE TO IMPROVE MEASUREMENT AND INFORMATION PROCESSING
271
