DISCRETE DYNAMIC SLIDING SURFACE CONTROL FOR

ROBUST SPEED CONTROL OF INDUCTION MACHINE DRIVE

Abdel Faqir

(1)

, Daniel Pinchon

(2)

, Rafiou Ramanou

(2)

and Sofiane Mahieddine

(2)

(1)

ECTEI – (Paris, France)

(2)

LTI - Institut Universitaire de Technologie de l’Aisne (GEII)

13, Avenue François Mitterrand

02880 Cuffies

France

Keywords: Induction machine, indirect field oriented control, sliding mode control.

Abstract: This paper proposes the discrete dynamic sliding surface control to guarantee the existence of discrete

sliding mode and reduce the chattering phenomena for speed control of induction machine drive.

In discrete systems, the controller does not control the system during the sampling interval. The great

chattering and large control signal are caused by the high switching gain. In this paper, the dynamic sliding

surface is introduced to overcome the drawback. By setting the initial value of the dynamic sliding surface,

the system can lock to the sliding surface quickly without high switching gain. The control signal can be

reduced and the chattering can be eliminated. Furthermore, the induction machine speed control system is

used to show this controller’s robustness to against the parameter variation and external load.

The speed of the induction machine is regulated using the indirect field oriented control (IFOC). Thus, after

the application of the IFOC technique by determining the decoupled model of the machine, a discrete

sliding surface controller has been applied. Simulation study is used to show the performances of the

proposed method and then validated by an experimental prototype.

1 INTRODUCTION

Field oriented control, published for the first time by

Blaschke in his pioneering work in 1972, consists in

adjusting the flux by a component of the current and

the torque by the other component. For this purpose,

it is necessary to choose a d-q reference frame

rotating synchronously with the rotor flux space

vector, in order to achieve decoupling control

between the flux and the produced torque. This

technique allows to obtain a dynamical model

similar to the DC machine.

This technique presents a major drawback.

Indeed the behavior of the machine and its command

is strongly affected by the variation of the rotor

resistance due to the temperature or by the variations

of the rotor inductance due to the saturation.

To eliminate this drawback, we propose in this

paper, an indirect field oriented method using two

sliding mode controllers. Once the decoupled model

of the machine is obtained, a discrete sliding surface

control is chosen with an appropriate switching.

Simulations have been carried out to verify the

effectiveness and the performances of the proposed

method.

2 SYSTEM DESCRIPTION AND

MACHINE MODELLING

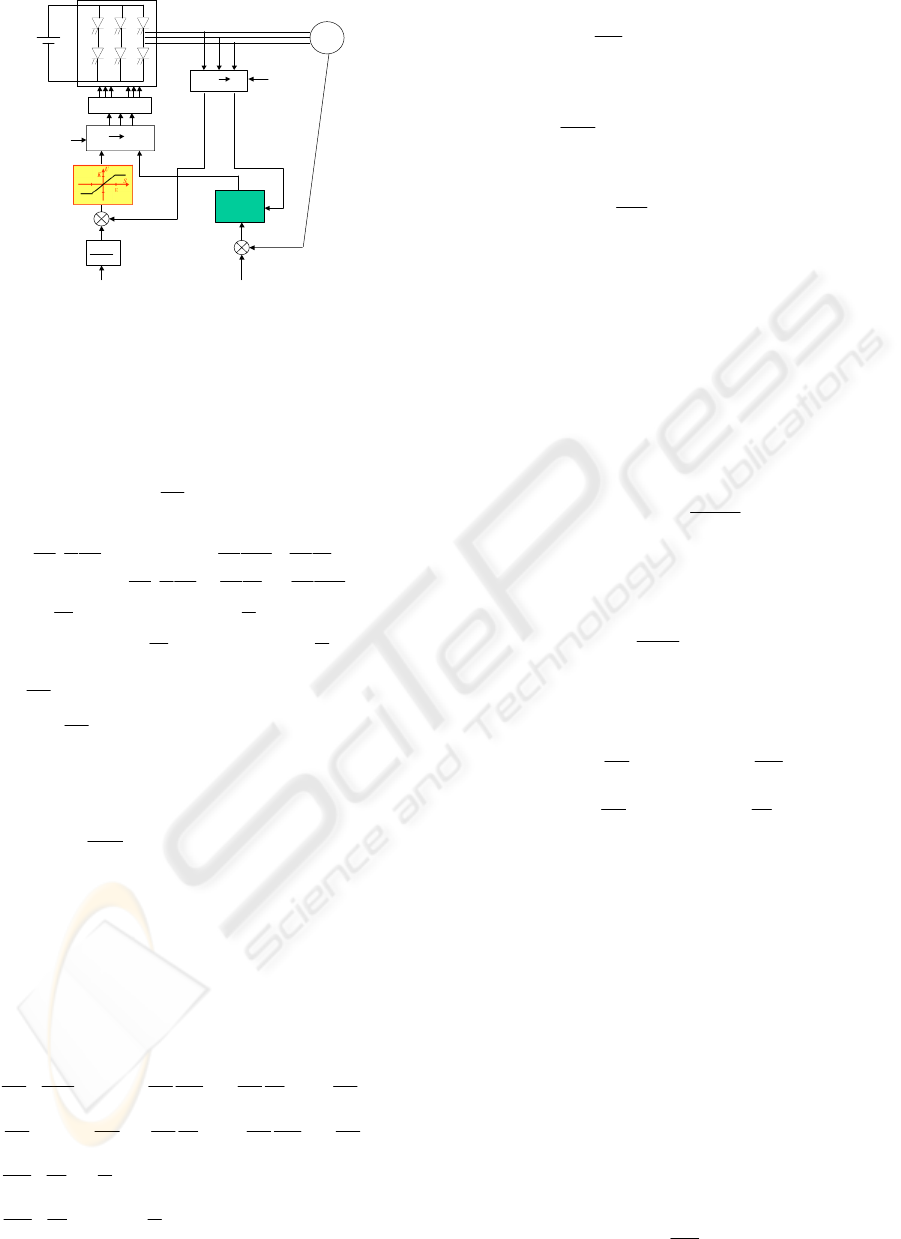
The system is an induction machine fed by a PWM

voltage source inverter. The sliding mode controllers

are applied to the inverter via reference voltages

(Fig. 1).

222

Faqir A., Pinchon D., Ramanou R. and Mahieddine S. (2007).

DISCRETE DYNAMIC SLIDING SURFACE CONTROL FOR ROBUST SPEED CONTROL OF INDUCTION MACHINE DRIVE.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 222-227

DOI: 10.5220/0001621602220227

Copyright

c

 SciTePress

SMC

DSSC

r

Ω

i

dsc

PWM Signals

IM

r

Ω

1+sT

r

L

m

()

ref

r

Ω

r

φ

s

θ

A,b,c d,q

i

ds

i

qs

V

qs

V

ds

s

θ

d,q A,b,c

i

a

i

b

i

c

v

a

v

b

v

c

Figure 1: Discrete Sliding Surface Control structure of an

induction machine.

2.1 Induction Machine Model

For the study of the induction machine, we take the

following model:

BUAX

dt

dX

+= (1)

with

(

)

(

)

⎥

⎦

⎤

⎢

⎣

⎡

−−

−

−−

−

+−−

−−−

+−

=

r

T

sl

r

T

m

L

sl

r

T

r

T

m

L

r

T

m

L

r

m

L

r

T

s

T

s

r

m

L

r

T

m

L

s

r

T

s

T

A

1

0

1

0

1111111

ω

σ

ω

σ

ω

σ

ω

σ

⎥

⎦

⎤

⎢

⎣

⎡

=

00

1

0

1

s

L

s

L

B

σ

,

⎥

⎦

⎤

⎢

⎣

⎡

=

qr

dr

qs

i

ds

i

X

φ

and

⎥

⎦

⎤

⎢

⎣

⎡

=

qs

v

ds

v

U

Where

⎟

⎠

⎞

⎜

⎝

⎛

−=

r

L

s

L

m

L

2

1

σ

.,

r

sl

sr

p

r

ωωωω

+=Ω=

The stator voltages

(

)

qs

v

ds

v ,

are considered as

control inputs, while the stator currents

(

)

qs

i

ds

i ,

, the

rotor flux

(

)

qr

dr

φφ

,

and the speed

(

)

r

Ω

are

considered as state variables.

From the equations (1), the following electrical

equations are deduced:

11 1

(2)

111

(3)

1

(4)

1

(5)

di

RLL

ds sm m m

ii v

sqs r qr

ds dr ds

dt L L T L L L L

ssrrsrs

di

RL L

qs

sm m m

ii v

sqs r qrqs

ds dr

dt L L L L T L L

ssr srr s

d

L

dr m

i

qr

ds dr sl

dt T T

rr

d

L

qr

m

i

qs qr

sl dr

dt T T

rr

ωφωφ

σσσσ

ωωφφ

σσ σ σ

φ

φωφ

φ

ωφ φ

−

=++ + +

=− − − + +

=−+

=−−

⎧

⎪

⎨

⎪

⎩

With

r

R

r

L

m

L

s

R

sm

R

2

+=

The mechanical model is given by:

r

f

K

L

T

em

T

dt

r

d

J Ω−−=

Ω

(6)

And the electromagnetic torque can be expressed as:

()

ds

i

qrqs

i

dr

r

L

m

pL

em

T

φφ

−=

(7)

2.2 Field Oriented Control

The field orientation is obtained by imposing:

⎩

⎨

⎧

=

0

qr

r

dr

φ

φφ

(8)

From the equations (4) and (8), the

ds

i

reference can

be computed in order to impose the flux

r

φ

:

ds

i

r

sT

m

L

r

+

=

1

φ

(9)

Furthermore, the position

s

θ

of the rotating frame

can be estimated using equations (5) and (8):

∫

Ω+=

⎟

⎠

⎞

⎜

⎝

⎛

dt

r

p

rr

T

qs

i

m

L

s

φ

θ

(10)

With taking into account the field orientation of the

machine, the stator equations on d-q axis become:

⎪

⎩

⎪

⎨

⎧

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

+++=

−−+=

rr

r

L

m

L

ds

i

ss

L

qs

i

sm

R

dt

qs

di

s

L

qs

V

r

L

r

T

m

L

qs

i

ss

L

ds

i

sm

R

dt

ds

di

s

L

ds

V

φωωσσ

φωσσ

(11)

2.3 Decoupling System

Using the system given by equations (11), we can

remark the interaction of both inputs, which makes

the control design more difficult.

The first step of our work is to obtain a

decoupled system in order to control the

electromagnetic torque via stator quadrature current

qs

i

such as a DC machine.

A decoupled model can be obtained by using two

intermediate variables:

d

emf

ds

v

ds

v +=

1

(12)

q

emf

qs

v

qs

v +=

1

(13)

where

rr

R

r

L

m

L

qs

i

s

L

s

d

emf

φσω

2

+=

(14)

DISCRETE DYNAMIC SLIDING SURFACE CONTROL FOR ROBUST SPEED CONTROL OF INDUCTION

MACHINE DRIVE

223

and

qs

i

r

T

r

L

m

L

r

L

m

L

s

ds

i

s

L

sq

emf

2

+−−=

φωσω

(15)

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

−

=

qs

i

ds

i

M

qs

v

ds

v

1

⎥

⎦

⎤

⎢

⎣

⎡

=

L

M

0

with

s

r

T

r

L

s

L

m

L

r

T

r

L

s

R

r

T

r

L

σ

++

=

2

(16)

The stator voltages

(

)

qs

v

ds

v

, are reconstituted from

(

)

1

,

1

qs

v

ds

v

(Fig. 2):

1/L

i

ds

i

qs

v

ds

v

qs

+

-

+

v

qs1

v

ds1

emf

d

emf

q

-

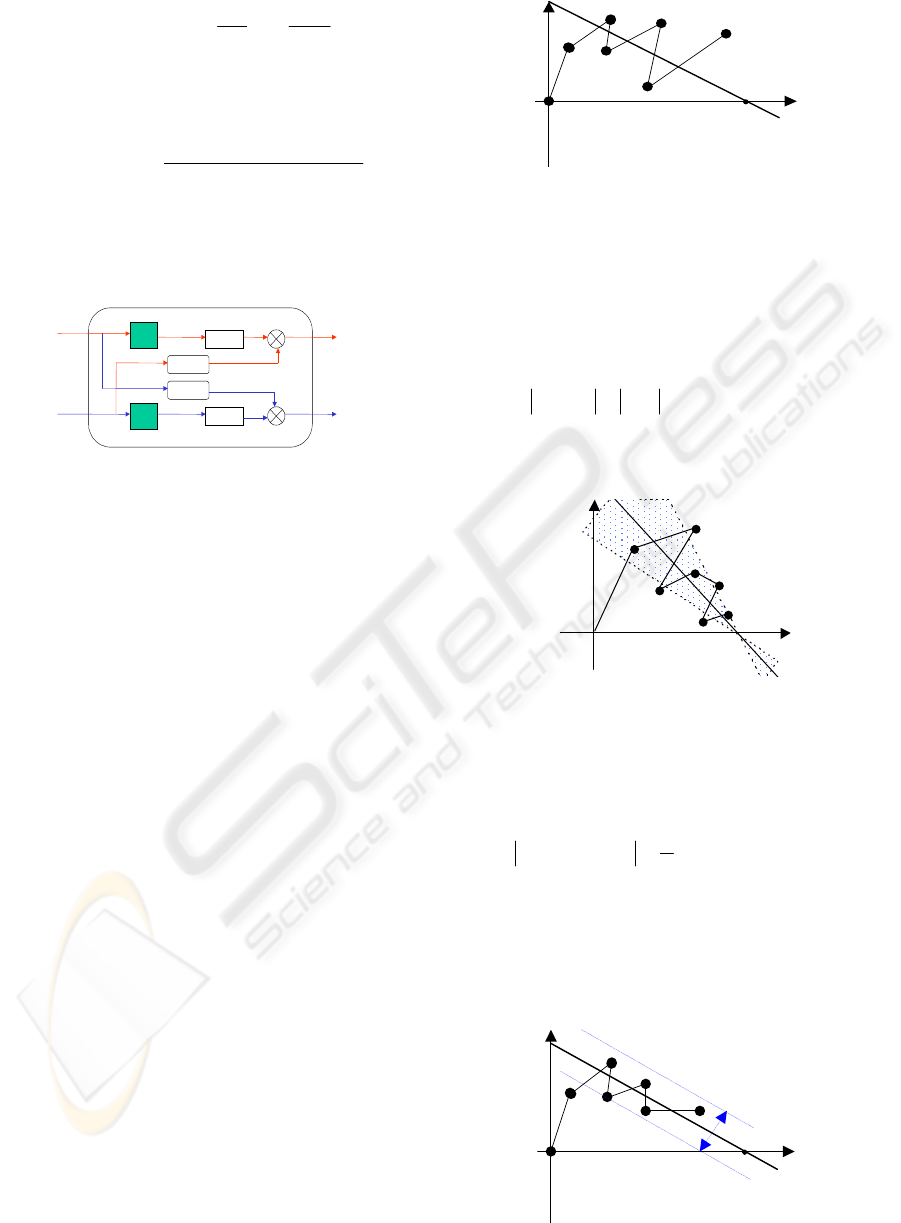
Figure 2: Decoupling control.

3 DISCRETE SLIDING SURFACE

CONTROL

3.1 General Concept

Since Dr. Utkin proposed the variable structure

system (VSS), it had been widely discussed and

applied in many control systems. Due to the change

of the switching gains in control function, the

controlled system can vary its own controller

according to the external condition. Hence, VSS is

robust to against to the system‘s parameter variation

and external disturbance. VSS owns one sliding

surface predetermined according to the desired

dynamic character. Once the sliding mode locking

on the sliding surface, the system response will be

directed by this surface. The existence condition of

classical sliding mode in continuous system is

0SS <



(17)

Change the differential equation to difference

equation. When applying the condition to discrete

systems, the existence condition becomes to

() ( )

(

)

[]

0kS1kSkS <−+

(18)

However, the system is controlled by the controller

only in each sampling time. The controller can not

modify the response during the sampling interval. It

may happen that the condition (18) is not only

satisfied but also the sliding motion is divergent. It is

shown in fig 3.

Phase Plane

S(k)

S(k+1)

S(k+2)

S(k+3)

Ω

ref

Figure 3: Discrete sliding mode.

The condition (18) only makes the sliding motion

toward to the sliding surface. However, it can not

guarantee the sliding mode convergent to this

surface. The condition (18) is only the necessary

condition not the sufficient condition in discrete

systems. To make up the drawback, we introduces

one additional restriction, that is

(

)

(

)

kS1kS <+

(19)

Combining equation (18) and (19) can make sure the

sliding motion convergent. However, the sliding

surface is changed to sliding region shown in fig 4.

S(k)

Phase Plane

S(k+1)

S( k+ 2)

S(k+3)

Figure 4: Discrete sliding mode with sliding region.

The choice of switching gain becomes three states.

This change causes some difficulty in

implementation of hardware. To maintain the binary

choice, one restriction of different viewpoint, that is

()()

2

kS1kS

ξ

<−+

(20)

where

ξ

is a small positive constant. The varying of

each step of sliding motion is restricted. Then,

condition (18) makes the sliding mode toward to the

surface. The condition (20) makes the sliding motion

oscillated on this surface within a small range

ξ

shown in fig 5.

Phase Plane

S(k)

S(k+1)

S(k+2)

S(k+3)

Ω

ref

ξ

Ω



Figure 5: New discrete sliding mode.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

224

This new sliding mode is

()

ξ<kS

different to the

classical sliding mode

(

)

0kS =

. Hence, this new

sliding mode is called “non-ideal sliding mode.”

This paper will prove that if the controller makes the

system‘s solution of classical sliding mode

asymptotically stable, then the same controller

makes the solution of non-ideal sliding mode

asymptotically stable, too. Hence, the discussion of

non-ideal sliding mode can be done like classical

sliding mode. Just like the classical sliding mode,

the system’s dynamic character is directed by the

surface only when the sliding motion is within the

range of

ξ

. To reduce the time of out of control, the

high switching gain is usually chosen to speed up the

reaching time. However, in discrete systems the

controller only modifies the control signal at each

sampling time. High switching gains can speed up

the reaching time, but the chattering often be

enlarged. To eliminate the chattering and decrease

the reaching time, this paper introduces the dynamic

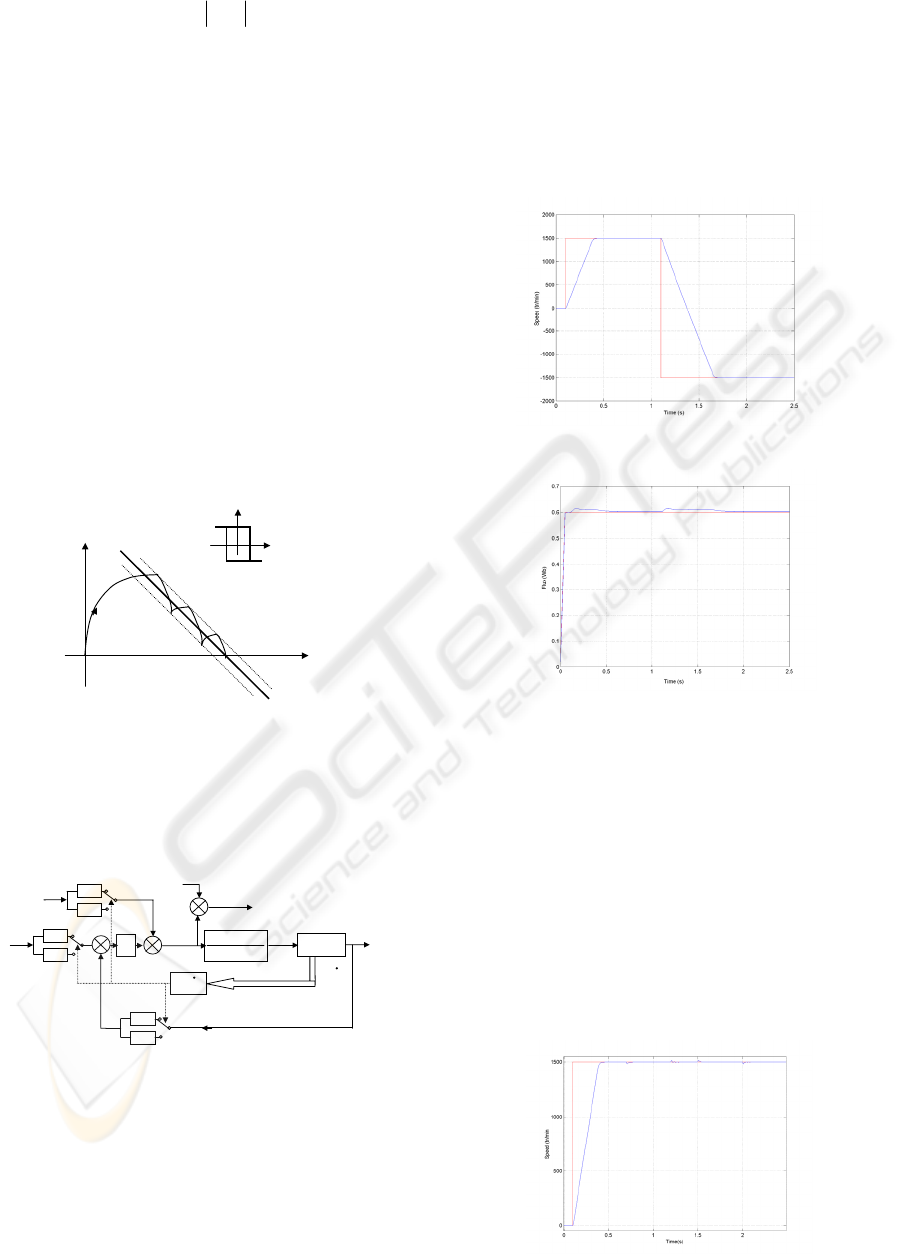
sliding surface control (DSSC) rule shown in fig 6.

u = U

min

u=U

max

S(k) = 0

U

S(k)

ref

Ω



Figure 6: Discrete sliding mode with dynamic sliding

surface.

5 SIMULATION RESULTS

S(

Ω

,

Ω

)

Ω

V

qs1

p.L

m

.

φ

r

.L

r

R

s

.L

r

2

+ R

s

.L

r

2

T

em

H=1

Ω

ref

+

-

K

i

/s

1/J.s+F

H=-1

G=1

G=-1

+

m

1

-1

u

2

u

1

Ω

,

Ω

V

qs

fem

q

-

+

-

Figure 7: Scheme of speed sliding mode regulation.

The proposed scheme has been simulated using

parameters given in the appendix.

The first simulation realized on the AC machine

consists in step variation of the reference. Indeed,

(Fig. 8) and (Fig. 9) represent the speed and the rotor

flux when reference step is first imposed and then an

inversion is imposed.

In (Fig. 9) it is clearly shown for rotor flux responses

that the decoupling is realized since the direct

component of the rotor flux converges to the

reference

(

)

ref

r

φ

, and its quadrature component to

zero despite the reference variations. Furthermore

we can remark that the proposed control scheme

presents good tracking capacities since there is no

overshoot and no static error (Fig. 8).

Figure 8: Speed response.

Figure 9: Rotor flux components responses.

(Fig. 10) represents the dynamic response of the

speed for different values of the load torque. First

when the speed reaches its reference value (1500

tr/min), a step of load torque is applied at (t=0.7 s).

The electromagnetic torque rises to the new value of

the load torque (Fig.11), and the speed is not

disturbed. Then when the load torque is decreased to

zero (t=1.2 s) or to a negative value (t=1.5 s) the

speed stays on the reference value.

It is clearly shown from the results that the control

scheme presents good regulation capacities. Indeed,

the external disturbances such as load torque

variations are rejected by control system.

Figure 10: Speed response to load torque variations.

DISCRETE DYNAMIC SLIDING SURFACE CONTROL FOR ROBUST SPEED CONTROL OF INDUCTION

MACHINE DRIVE

225

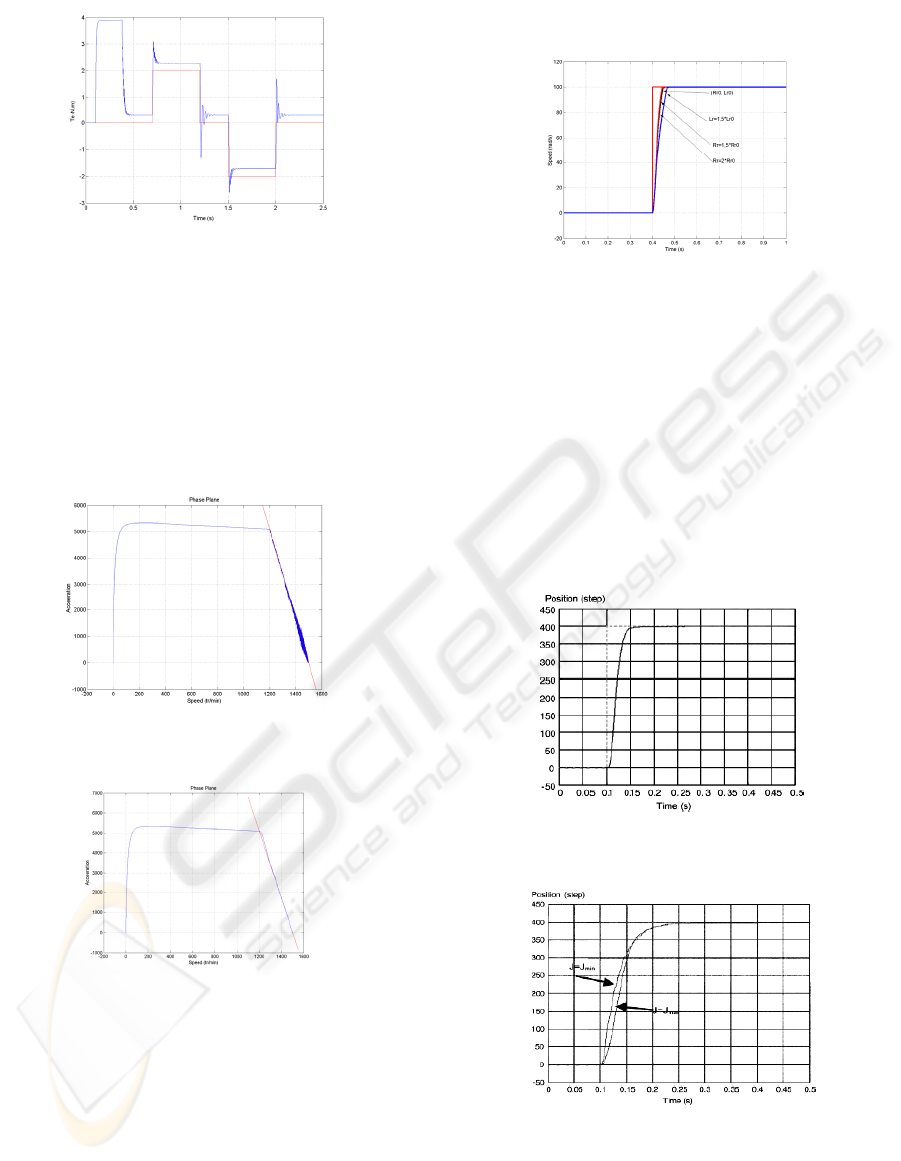
Figure 11: Electromagnetic torque responses to load

torque variations.

(Fig. 12) and (Fig. 13) illustrate the dynamic

response in the phase plane respectively with a

normal sliding surface control and with a dynamic

discrete sliding surface control.

We can note the apparition of the chattering

phenomenon (Fig. 12) with the normal sliding

surface control due to the discontinuous

characteristic of this function.

Figure 12: Response in the phase plane with the normal

sliding surface control.

Figure 13: Response in the phase plane with dynamic

discrete sliding surface control.

(Fig. 14) depicts the drive response for different

values of the rotor constant time.

It is important to note that the changing parameters

are introduced only in the model of the machine.

The controller is not involved by these variations.

It is well-known for classic controller that the

indirect field oriented control is very sensitive to the

rotor constant time variations.

The results shown on (Fig. 14) confirm the

robustness quality inherent to the proposed

controller. Indeed, there is no overshot whatever the

rotor constant time

Figure 14: Robustness test of the sliding mode control.

6 EXPERIMENTAL RESULTS

Figs. 15 and 16 show the experimental evolution of

the position and the experimental phase plane

trajectory when the sliding condition is just

validated: |c_| = |s1p|. It can be seen that the step

reference of 400 steps is reached for t = 0.08 s

without overshoot or steady-state error and that there

are almost three commutations to reach the

reference.

Figure 15: Position and reference (400 steps).

Figure 16: Position and reference for two different

inertias.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

226

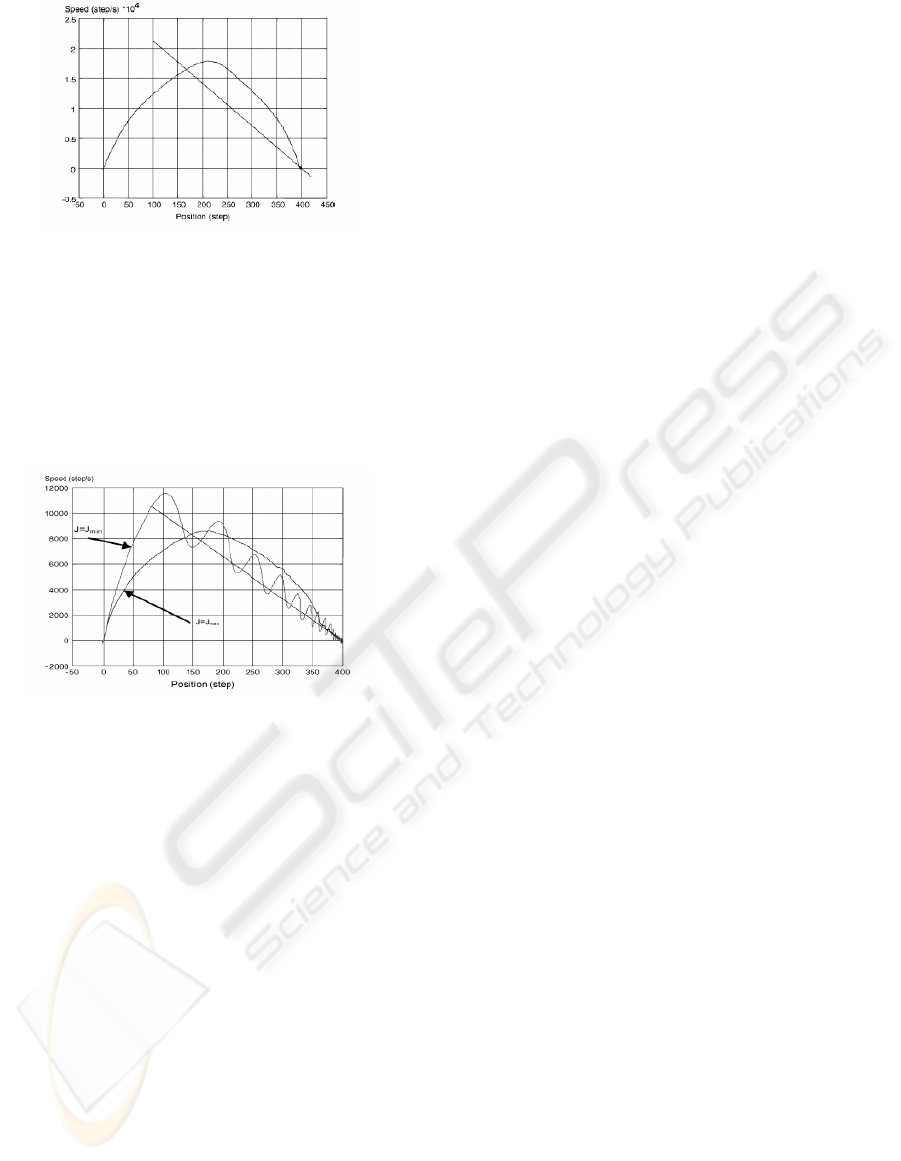
Figure 17: Phase plane trajectory.

Figs. 17 and 18 show the evolution of the position

and the phase plane trajectories for two different

inertias (J = Jmin = 0.0023 kg.m

2

and J = Jmax =

0.013485 kg.m

2

).

By comparing the two responses, it can be noted that

the reference is always reached without any

overshoot or steady-state error whatever the inertia

of the drive.

Figure 18: Phase plane trajectory for two different inertias.

From these results, it can be seen that the robustness

of the proposed approach between external

disturbances and plant parameter variations is

experimentally validated.

7 CONCLUSION

In this paper, we have shown that by using a sliding

mode control applied to an IFOC, a high-precision

positioning of an IM shaft can be achieved whatever

the mechanical configuration of the load is. Indeed,

the position reference is obtainedwithout any

overshoot or static errorwhatever the inertia or the

load torque are. Furthermore, it has been shown that

the chattering problem around the switching surface

can be alleviated using the VSC approach with

LFSG. Therefore, the proposed solution can be

considered very suitable for induction drive used in

robotics or in numerical control of machine tools.

REFERENCES

M.O. Mahmoudi et al, Cascade sliding mode control of a

field oriented induction machine drive, EDP Sciences

(1999).

Guy Grellet, Guy Clerc, Actionneurs elctrique

(EYROLLES, France, 1997).

Vadim I.Utkin, IEEE Transactions on industrial

electronics (Vol 40, No 1, 1993)

H. Bühler, Réglage par mode de glissement (Presses

polytechniques romandes, Switzerland, 1986).

F. Chen and M. W. Dunnigan, “Sliding-mode torque and

flux control of an induction machine,” Proc. IEE

Electric Power Appl., vol. 150, no. 2, pp. 227–236,

Mar. 2003.

P. DeWit, R. Ortega, and I. Mareels, “IFOC of

inductionmotors is robustly globally stable,”

Automatica, vol. 32, no. 10, Oct. 1996.

Abdel Faqir, “Position Control of an Induction Machine

Using Variable Structure Control”, thesis (2003).

S. Ferreira Pinto, Sliding mode control of matrix

converters with lead-lag power factor, EPE (2001).

E. Etien, Real time induction motor drive using sliding

mode linearization, EPE (2001).

Jesus Arellano-Padilla, Robust fuzzy-sliding mode control

for motor drives operating with variable loads and pre-

defined system noise limits, EPE (2001).

LIST OF PRINCIPAL SYMBOLS

p

: Number of pole pairs.

rs

RR , : Stator and rotor resistance.

rs

LL , : Stator and rotor inductance.

:

r

T

Rotor time constant.

m

L : Magnetizing inductance.

qsds

ii , : Stator currents in d-q rotating reference

frame.

qsds

vv , : Stator voltages d-q rotating reference

frame.

qrdr

φ

, : Rotor fluxes d-q rotating reference frame.

r

ω

: Rotor speed.

e

T : Electromagnetic torque.

s

θ

: Angular position.

s : Laplace operator

(

)

dtd /

.

σ

: Coefficient of dispersion.

J : Total rotor inertia constant.

DISCRETE DYNAMIC SLIDING SURFACE CONTROL FOR ROBUST SPEED CONTROL OF INDUCTION

MACHINE DRIVE

227