FAST COMPUTATION OF ENTROPIES

AND MUTUAL INFORMATION FOR MULTISPECTRAL IMAGES

e Ouattara, Alain Cl

ement and Franc¸ois Chapeau-Blondeau

Laboratoire d’Ing

enierie des Syst

emes Automatis

es (LISA), Universit

e d’Angers

62 avenue Notre Dame du Lac, 49000 Angers, France

Keywords:

Multispectral images, Entropy, Mutual information, Multidimensional histogram.

Abstract:

This paper describes the fast computation, and some applications, of entropies and mutual information for

color and multispectral images. It is based on the compact coding and fast processing of multidimensional

histograms for digital images.

1 INTRODUCTION

Entropies and mutual information are important tools

for statistical analysis of data in many areas. For im-

age processing, so far, these tools have essentially

been applied to scalar or one-component images. The

reason is that these tools are usually derived from

multidimensional histograms, whose direct handling

is feasible only in low dimension due to their memory

occupation and related processing time which become

prohibitively large as the number of image compo-

nents increases. Here, we use an appraoch for multi-

dimensional histograms allowing compact coding and

fast computation, and show that this approach easily

authorizes the computation of entropies and mutual

information for multicomponent or multispectral im-

ages.

2 A FAST AND COMPACT

MULTIDIMENSIONAL

HISTOGRAM

We consider multispectral images with D components

), for i = 1 to D, each X

varying among Q

possible values, at each pixel of spatial coordinate

). A D-dimensional histogram of such an im-

age would comprise Q

cells. For an image with

×N

= N pixels, only at most N of these Q

cells

can be occupied, meaning that, as D grows, most of

the cells of the D-dimensional histogram are in fact

empty. For example, for a common 512 ×512 RGB

color image with D = 3 and Q = 256 = 2

, there are

= 2

≈ 16×10

colorimetric cells with at most

only N = 512

= 262144 of them which can be occu-

pied. We developed the idea of a compact represen-

tation of the D-dimensional histogram (Cl

ement and

Vigouroux, 2001; Cl

ement, 2002), where only those

cells that are occupied are coded. The D-dimensional

histogram is coded as a linear array where the entries

are the D-tuples (the colors) present in the image and

arranged in lexicographic order of their components

,...X

). To each entry (in number ≤ N) is as-

sociated the number of pixels in the image having this

D-value (this color). An example of this compact rep-

resentation of the D-dimensional histogram is shown

in Table 1.

The practical calculation of such a compact his-

togram starts with the lexicographic ordering of the

N D-tuples corresponding to the N pixels of the im-

age. The result is a linear array of the N ordered D-

tuples. This array is then linearly scanned so as to

merge the neighboring identical D-tuples while accu-

mulating their numbers to quantify the correspond-

ing population of pixels. With a dichotomic quick

sort algorithm to realize the lexicographic ordering,

the whole process of calculating the compact multidi-

mensional histogram can be achieved with an average

complexity of O(N logN), independent of the dimen-

sion D. Therefore, both compact representation and

its fast calculation are afforded by the process for the

195

Ouattara S., Clément A. and Chapeau-Blondeau F. (2007).

FAST COMPUTATION OF ENTROPIES AND MUTUAL INFORMATION FOR MULTISPECTRAL IMAGES.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 195-199

DOI: 10.5220/0001622801950199

 SciTePress

Table 1: An example of compact coding of the 3-

dimensional histogram of an RGB color image with Q =

256. The entries of the linear array are the components

) = (R, G, B) arranged in lexicographic order,

for each color present in the image, and associated to the

poupulation of pixels having this color.

R G B population

0 0 4 13

0 0 7 18

0 0 23 7

255 251 250 21

255 251 254 9

multidimensional histogram.

For example, for a 9-component 838×762 satel-

lite image with Q = 2

, the compact histogram

was calculated in about 5 s on a standard 1 GHz-

clock desktop computer, with a coding volume of

1.89Moctets, while the classic histogram would take

3.60×10

Moctets completely unmanageable by to-

day’s computers.

3 ENTROPIES AND MUTUAL

INFORMATION FOR IMAGES

3.1 Fast Computation from Compact

Histogram

The multidimensional histogram of an image, after

normalization by the number of pixels, can be used

for an empirical deﬁnition of the probabilities p(

associated to the D-values present in image

X. In the

compact histogram, coded as in Table 1, only those D-

values of

X with nonzero probability are represented.

This is all that is needed to compute any property of

the image that is deﬁned as a statistical average over

the probabilities p(

X). This will be the case for the

statistical moments of the distribution of D-values in

the image (Romantan et al., 2002), for the principal

axes based on the cross-covariances of the compo-

nents X

(Plataniotis and Venetsanopoulos, 2000), and

for the entropies, joint entropies and mutual informa-

tion that we consider in the sequel.

An entropy H(

X) for image

X can be deﬁned as

(Russ, 1995)

X) = −

∑

X)log p(

X) . (1)

The computation of H(

X) of Eq. (1) from the nor-

malized compact histogram from Table 1, is realized

simply by a linear scan of the array while summing

the terms −p(

X)logp(

X) with p(

X) read from the

last column. This preserves the overall complexity of

O(N logN) for the whole process leading to H(

X).

The compact histogram also allows one to en-

visage the joint entropy of two multicomponent im-

ages

X and

Y, with dimensions D

and D

respec-

tively. The joint histogram of (

Y) can be calculated

as a compact histogram with dimension D

+ D

which after normalization yields the joint probabili-

ties p(

Y) leading to the joint entropy

Y) = −

∑

Y) log p(

Y) . (2)

A mutual information between two multicomponent

images follows as

Y) = H(

X)+ H(

Y) −H(

Y) . (3)

And again, the structure of the compact histogram

preserves the overall complexity of O(N logN) for the

whole process leading to H(

Y) or I(

Y).

So far in image processing, joint entropies and

mutual information have essentially been used for

scalar or one-component images (Likar and Pernus,

2001; Pluim et al., 2003), because the direct handling

of joint histograms is feasible only in low dimension,

due to their memory occupation and associated pro-

cessing time which get prohibitively large as dimen-

sion increases. By contrast, the approach of the com-

pact histogram of Section 2 makes it quite tractable to

handle histograms with dimensions of 10 or more. By

this approach, many applications of entropies and mu-

tual information become readily accessible to color

and multispectral images. We sketch a few of them in

the sequel.

3.2 Applications of Entropies

The entropy H(

X) can be used as a measure of com-

plexity of the multicomponent image

X, with applica-

tion for instance to the following purposes:

• An index for characterization / classiﬁcation of tex-

tures, for instance for image segmentation or classiﬁ-

cation purposes.

• Relation to performance in image compression, es-

pecially lossless compression.

For illustration, we use the entropy of Eq. (1) as

a scalar parameter to characterize RGB color images

carrying textures as shown in Fig. 1. The entropies

X) given in Table 2 were calculated from 512×512

three-component RGB images

X with Q = 256. The

whole process of computing a 3-dimensional his-

togram and the entropy took typically less than one

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

196

second on our standard desktop computer. For com-

parison, another scalar parameter σ(

X) is also given

in Table 2, as the square root of the trace of the

variance-covariance matrix of the components of im-

age

X. This parameter σ(

X) measures the overall

average dispersion of the values of multicomponent

image

X. For a one-component image

X, this σ(

would simply be the standard deviation of the gray

levels. The results of Table 2 show a speciﬁc signif-

icance for the entropy H(

X) of Eq. (1), which does

not simply mimic the evolution of a common mea-

sure like the dispersion σ(

X). As a complexity mea-

sure, H(

X) of Eq. (1) is low for synthetic images as

Chessboard

and

Wallpaper

, and is higher for natu-

ral images in Table 2.

Chessboard

Wallpaper

Clouds

Wood

Marble

Bricks

Plaid

Denim

Leaves

Figure 1: Nine three-component RGB images

X with Q =

256 carrying distinct textures.

3.3 Applications of Mutual Information

The mutual information I(

Y), or other measures

derived from the joint entropy H(

Y), can be used

as an index of similarity or of relationship, between

two multicomponent images

X and

Y, with applica-

tion for instance to the following purposes:

• Image matching, alignment or registration, espe-

cially in multimodality imaging.

• Reference matching, pattern matching, for pattern

recognition.

• Image indexing from databases.

Table 2: For the nine distinct texture images of Fig. 1: en-

tropy H(

X) of Eq. (1) in bit/pixel, and overall average dis-

persion σ(

X) of the components.

texture H(

X) σ(

Chessboard 1.000 180.313

Wallpaper 7.370 87.765

Clouds 11.243 53.347

Wood 12.515 31.656

Marble 12.964 44.438

Bricks 14.208 57.100

Plaid 14.654 92.284

Denim 15.620 88.076

Leaves 17.307 74.966

• Homogeneity / contrast assessment for segmenta-

tion or classiﬁcation purposes.

•Performance evaluation of image reconstruction, es-

pecially in lossy compression.

• Analysis via principal, or independent, component

analysis.

For illustration, we consider a lossy compression

on an RGB color N

×N

image

X via a JPEG-like

operation consisting, on the N

×N

discrete cosine

transform of

X, in setting to zero a given fraction (1−

−1

) of the high frequency coefﬁcients, or equiva-

lently in retaining only the N

√

CR × N

√

CR low-

frequency coefﬁcients. From this lossy compression

of initial image

X, the decompression reconstructs a

degraded image

Y. While varying the compression

ratio CR, the similarity between images

X and

Y is

measured here by the mutual information I(

Y) of

Eq. (3) based on the 6-dimensional joint histogram

for estimating the joint probabilities p(

Y). In ad-

dition, for comparison, we also used a more common

measure of similarity formed by the cross-correlation

coefﬁcient C(

Y) between

X and

Y, computed as

one third of the sum of the cross-correlation coefﬁ-

cient between each marginal scalar component, R, G

or B, of

X and

Y. This C(

Y) = 1 if

X and

Y are

two identical images, and it goes to zero if

X and

are two independent unrelated images. For the re-

sults presented in Fig. 2, the choice for initial im-

age

X is a 512×512 RGB

lena.bmp

with Q = 256.

The whole process of the computation of an instance

of the 6-dimensional joint histogram and the mutual

information took around 3s on our standard desktop

computer.

Figure 2 shows that, as the compression ratio

CR increases, the mutual information I(

Y) and the

cross-correlation coefﬁcient C(

Y) do not decrease

in the same way. Compared to the mutual informa-

tion I(

Y), it is known that the cross-correlation

FAST COMPUTATION OF ENTROPIES AND MUTUAL INFORMATION FOR MULTISPECTRAL IMAGES

197

0.8

0.85

0.9

0.95

compression ratio

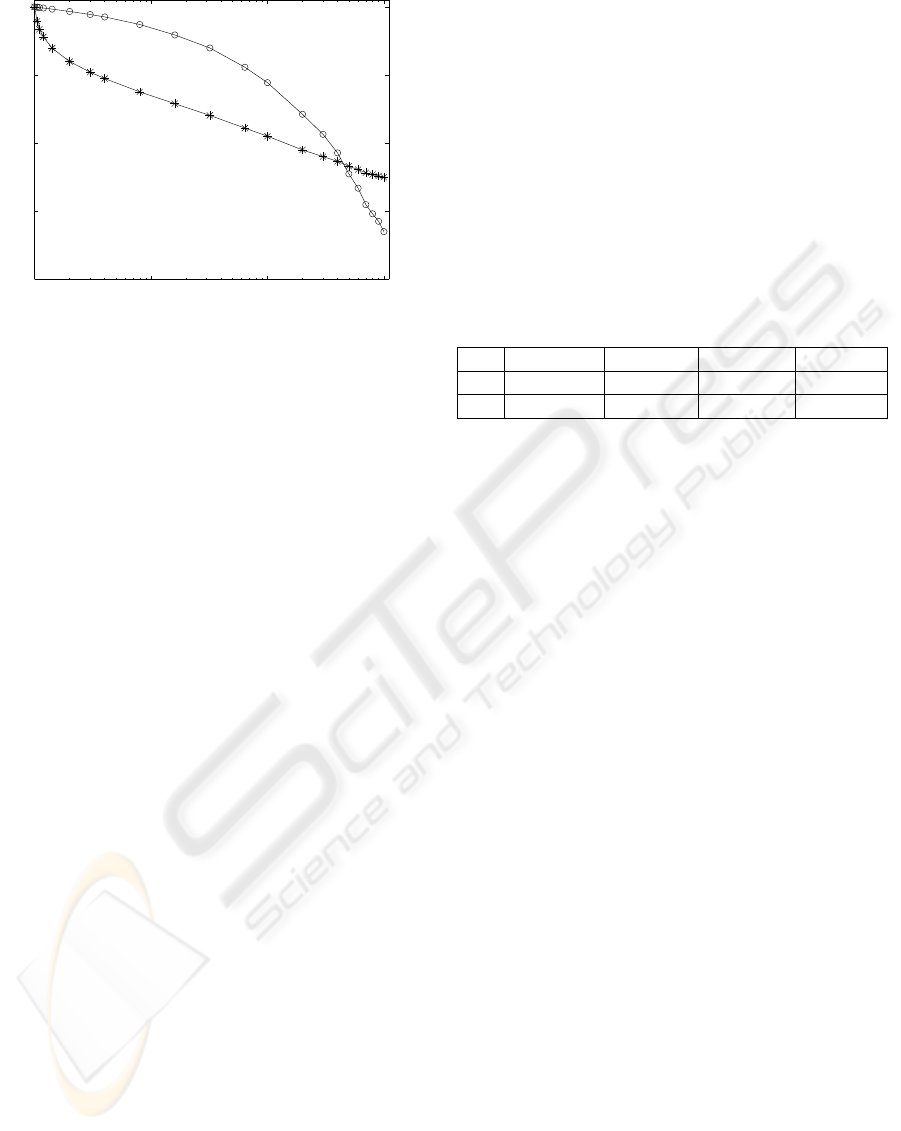
Figure 2: As a function of the compression ratio CR: (◦)

cross-correlation coefﬁcient C(

Y) between initial RGB

color image

X and its compressed version

Y; (∗) normalized

mutual information I(

Y)/H(

X) with the entropy H(

X) =

16.842 bits/pixel.

Y) measures only part of the dependence be-

tween

X and

Y. Figure 2 indicates that when the com-

pression ratio CR starts to rise above unity, I(

decreases faster than C(

Y), meaning that informa-

tion is ﬁrst lost at a faster rate than what is captured

by the cross-correlation. Meanwhile, for large CR in

Fig. 2, I(

Y) comes to decrease slower thanC(

Y).

This illustrates a speciﬁc contribution of the mutual

information computed for multicomponent images.

Another application of mutual information be-

tween images can be found to assess a principal com-

ponent analysis. On a D-component image

X =

,...X

), principal component analysis applies a

linear transformation of the X

’s to compute D prin-

cipal components (P

,...P

) with vanishing cross-

correlation among the P

’s, in such a way that some

’s can be selected for a condensed parsimonious

representation of initial image

X. An interesting

quantiﬁcation is to consider the mutual information

X,P

). From its theoretical properties, the joint en-

tropy H(

X,P

) reduces to H(

X) because P

is deter-

ministically deduced from

X, henceforth I(

X,P

) =

H(P

). This relationship has been checked (on sev-

eral 512×512 RGB color images with D = 3) to be

precisely veriﬁed by our empirical entropy estima-

tors for I(

X,P

) based on the computation of (D+ 1)-

dimensional histograms for (

X,P

). This offers a

quantiﬁcation of the relation between

X and its prin-

cipal components P

; a subset of the whole P

’s could

be handled in a similar way. Another useful quantiﬁ-

cation shows that principal component analysis, al-

though it cancels cross-correlation between the com-

ponents, does not cancel dependence between them,

and sometimes it may even increase it in some sense,

as illustrated by the behavior of the mutual informa-

tion in Table 3, with I(P

) larger than I(X

)

for image (2). The mutual information can serve as a

measure to base other separation or selection schemes

of the components from an initial multispectral im-

age

Table 3: For a 512 ×512 RGB color image

X with D = 3

and Q = 256: cross-correlation coefﬁcient C(·, ·) and mu-

tual information I(·,·) of Eq. (3), between the two initial

components X

and X

with largest variance, and between

the two ﬁrst principal components P

and P

after principal

component analysis of

X. (1) image

X is

lena.bmp

. (2)

image

X is

mandrill.bmp

C(X

) I(X

) C(P

) I(P

)

(1) 0.879 1.698 0.000 0.806

(2) 0.124 0.621 0.000 0.628

4 CONCLUSION

We have reported the fast computation and compact

coding of multidimensional histograms and showed

that this approach authorizes the estimation of en-

tropies and mutual information for color and multi-

spectral images. Histogram-based estimators of these

quantities as used here, become directly accessible

with no need of any prior assumption on the images.

The performance of such estimators clearly depends

on the dimension D and size N

×N

of the images;

we did not go here into performance analysis, espe-

cially because this would require to specify statistical

models of reference for the measured images. Instead

here, more pragmatically, on real multicomponent im-

ages, we showed that, for entropies and mutual in-

formation, direct histogram-based estimation is feasi-

ble and exhibits natural properties expected for such

quantities (complexity measure, similarity index, . ..).

The present approach opens up the way for further ap-

plication of information-theoretic quantities to multi-

spectral images.

REFERENCES

ement, A. (2002). Algorithmes et outils informatiques

pour l’analyse d’images couleur. Application

a l’

etude

de coupes histologiques de baies de raisin en micro-

scopie optique. Ph. D. thesis, University of Angers,

France.

ement, A. and Vigouroux, B. (2001). Un histogramme

compact pour l’analyse d’images multi-composantes.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

198

In Proceedings 18

e Colloque GRETSI sur le Traite-

ment du Signal et des Images, pages 305–307,

Toulouse, France, 10–13 Sept. 2001.

Likar, B. and Pernus, F. (2001). A hierarchical approach to

elastic registration based on mutual information. Im-

age and Vision Computing, 19:33–44.

Plataniotis, K. N. and Venetsanopoulos, A. N. (2000). Color

Image Processing and Applications. Springer, Berlin.

Pluim, J. P. W., Maintz, J. B. A., and Viergever, M. A.

(2003). Mutual-information-based registration of

medical images: A survey. IEEE Transactions on

Medical Imaging, 22:986–1004.

Romantan, M., Vigouroux, B., Orza, B., and Vlaicu, A.

(2002). Image indexing using the general theory of

moments. In Proceedings 3rd COST 276 Workshop

on Information and Knowledge Management for Inte-

grated Media Communications, pages 108–113, Bu-

dapest, Hungary, 11–12 Oct. 2002.

Russ, J. C. (1995). The Image Processing Handbook. CRC

Press, Boca Raton.

FAST COMPUTATION OF ENTROPIES AND MUTUAL INFORMATION FOR MULTISPECTRAL IMAGES

199