ON COMPUTING MULTI-FINGER FORCE-CLOSURE GRASPS

OF 2D OBJECTS

Belkacem Bounab

* **

, Daniel Sidobre

** ‡

Mechanical Laboratory of Structures, EMP, Algiers, Algeria

LAAS-CNRS, Toulouse, France

‡

Paul Sabatier University, Toulouse, France

Abdelouhab Zaatri

Advanced Technologies Laboratory, Mentouri University, Constantine, Algeria

Keywords: Multi-Fingered grasps, Force-Closure, Cen

tral Axis, Grasp Wrenches.

Abstract: In this paper, we develop a new algorithm for

computing force-closure grasps of two-dimensional (2D)

objects using multifingred hand. Assuming hard-finger point contact with Coulomb friction, we present a

new condition for multi-finger to form force-closure grasps. Based on the central axis of contact wrenches,

an easily computable algorithm for force-closure grasps has been implemented and its efficiency has been

demonstrated by examples.

1 INTRODUCTION

Grasping remains one of the fundamental problems

in robotics. Research has been directed towards the

design and control of multifingred dexterous robot

hand to increase robot dexterity and adaptability (Li

J-W., Jin M-H. and Liu H. 2003).

A main property of a multi-finger stable grasp is

force-cl

osure. It’s the ability to balance any external

object wrenches by applying appropriate finger

wrenches at the contact points. In other words, a

grasp on an object is force-closure if and only if

arbitrary force and torque can be exerted on the

object through the fingers (Yan-Bin Jia 2004). It’s

complicated to assure that the applied finger forces

remain in the friction cone at all times so as to avoid

fingers slippage on the object surface (Murray R., Li

Z. and Sastry S. 1994).

Human can use more than three/four fingers of

s hand to manipulate objects. During such tasks,

there exists a lot of contact points between the hand

and grasped object. The question is: how can we

evaluate or compute force-closure of such grasps?

In this paper, we are focu

sed on the problem of

computing force-closure of multifingered grasps of

2D objects. We develop a new approach for force-

closure test independently of fingers's number. This

quality is obtained using the mechanical properties

of the grasp wrench.

2 RELATED WORK

Force-closure test is an essential problem in

grasping. However, The notion of force-closure does

not directly yield a method for force-closure test

(Sudsang A. and Phoka T. 2005). Some necessary

and sufficient conditions for force-closure were

formulated in order to derive force-closure tests. A

commonly used necessary and suffecient force-

closure condition given by (Salisbury J.K. and Roth

B. 1982) allowed a force-closure test to be

performed by checking whether the origin is strictly

inside the convex hull of the primitive contact

wrenches. This test also provided an underlying idea

to recent work in grasping (

D. Ding, Y-H Liu, and S.

Wang 2001

). Nguyen (Nguyen, V.D. 1988) formally

demonstrated for 2-fingered grasps that non-

marginal equilibrium grasps achieve force-closure.

Recently, (Li J-W., Jin M-H. and Liu H. 2003)

proposed a necessary and suffecient condition for 3-

fingered force-closure grasps based on (Ponce J. and

Faverjon B. 1995) and developed an algorithm for

three-finger force-closure test. Their method begins

by the processing of friction cones using an

253

Bounab B., Sidobre D. and Zaatri A. (2007).

ON COMPUTING MULTI-FINGER FORCE-CLOSURE GRASPS OF 2D OBJECTS.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 253-258

DOI: 10.5220/0001624102530258

 SciTePress

operation called disposition H, then, they attack the

problem of determining the intersection of the three

double-side friction cones.

The rest of the paper is organized as follow, in

section 3, we present the background of grasp

wrenches central axes and the relationship between

these axes and grasp force-closure. In section 4, we

propose a new multi-finger force-closure condition.

Hence, a novel algorithm is presented, which its

implementation needs little geometric computations.

In section 5, we present some multi-finger grasps

examples. Finally, we conclude with future works.

3 CENTRAL AXIS OF GRASP

WRENCHES

Based on Coulomb friction model, a contact force is

constrained to lie in a friction cone centered about

the internal surface normal at contact point.

Figure 1: Contact between the finger and an object

showing friction cone.

As shown in figure 1, a friction cone at is

bounded by vectors and , and any force is a

nonnegative combination of these two vectors. In 2D

case, contact forces are

m,...,iaa

iiiii

2211

=+= nnf

(1)

With

0≥0≥

21 ii

a,a

to avoid fingertips slippage.

m is the number of contact points.

If is the surface normal at the contact

point and is the friction angle that depends on

materials in contact (finger and object) then,

)N,2(Atanβ

iii

XYN=

(2)

and

⎟

⎠

⎞

⎜

⎝

⎛

)αβSin(

)αβCos(

; (3)

⎟

⎠

⎞

⎜

⎝

⎛

−

)αβSin(

)αβCos(

The contact wrench produced by reduced at the

point O is defined by

⎥

⎦

⎤

⎢

⎣

⎡

fOC

(4)

()

⎥

⎦

⎤

⎢

⎣

⎡

+×

2211

iiiii

iiii

nnOC

The external wrench applied by the robotic hand

on the grasped object is given by

⎥

⎦

⎤

⎢

⎣

⎡

o/c

io/c

∑

(5)

With

()

()()

∑

∑∑

2211

iiiiio/c

iiii

+×=

+==

nnOCτ

nnfF

(6)

finger

ect

In two-dimensional grasps case, we have

(

)

cycxc

,F,F 0=F

and (7)

()

o/zo/c

τ,, 00=τ

With

()

()()

⎪

⎩

⎪

⎨

⎧

+⋅=

∑

2211

∧

iiiiio/z

iiiicy

iiiicx

aaτ

aaF

nnOCZ

nnY

nnX

(8)

Poinsot’s theorem: “Every collection of wrenches

applied to a rigid body is equivalent to a force

applied along a fixed axis (central axis) and a

torque around the same axis” (Murray R., Li Z.,

Sastry S. 1994). Using this theorem, points of the

central axis of contact wrench are given by

⎪

⎩

⎪

⎨

⎧

0Fτ

0FF

τF

co/c

o/cc

ifλ

ifλ ≠

: (9)

(

ℜ∈λ

)

The axis is a directed line through a point.

For , the central axis is a line in the

0F ≠

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

254

(a)

(b)

(a)

(b)

direction going through the point such as

the point such as

()

0 co/cc

/ FτFOQ ×=

≠

()

0 co/cc

/ FτFOQ ×=

0F =

c o/c

0≠

0F ≠

For , the axis is a line in the

direction

going through the origin (Murray R., Li Z., Sastry S.

1994).

For , the axis is a line in the

direction

going through the origin (Murray R., Li Z., Sastry S.

1994).

0F =

c o/c

In two-dimentional case with non null forces

(

), the torque around the central axis is zero.

The force

is an invariant vector and always

parallel to

. Figure 2 shows the central axis in 2D

grasps when

. it is Characterized by the

following equation

In two-dimentional case with non null forces

(

), the torque around the central axis is zero.

The force

is an invariant vector and always

parallel to

. Figure 2 shows the central axis in 2D

grasps when

. it is Characterized by the

following equation

0F ≠

⎟

⎠

⎞

⎜

⎝

⎛

+⋅

⎟

⎠

⎞

⎜

⎝

⎛

o/z

(10)

Figure 2: Central axis parameters.

In figure 3-a, we present a first example of three-

finger 2D grasp. By varying forces randomly (in

orientation and amplitude) inside friction cones (the

friction angle), figure 3-b illustrates all possible

central axes of grasp wrenches.

There is no central axis passing through the gray

region. In this region, positive torque can’t be

exerted on the object through the finger contacts.

This grasp can’t achieve force-closure. Exactly, the

grasp can not achieve torque-closure because the

object turn around the gray region in figure 3-a.

Figure 3: a) no force-closure 2D grasp, b) all central axes

of grasp wrenches ( ).

°= 5α

°= 10α

)

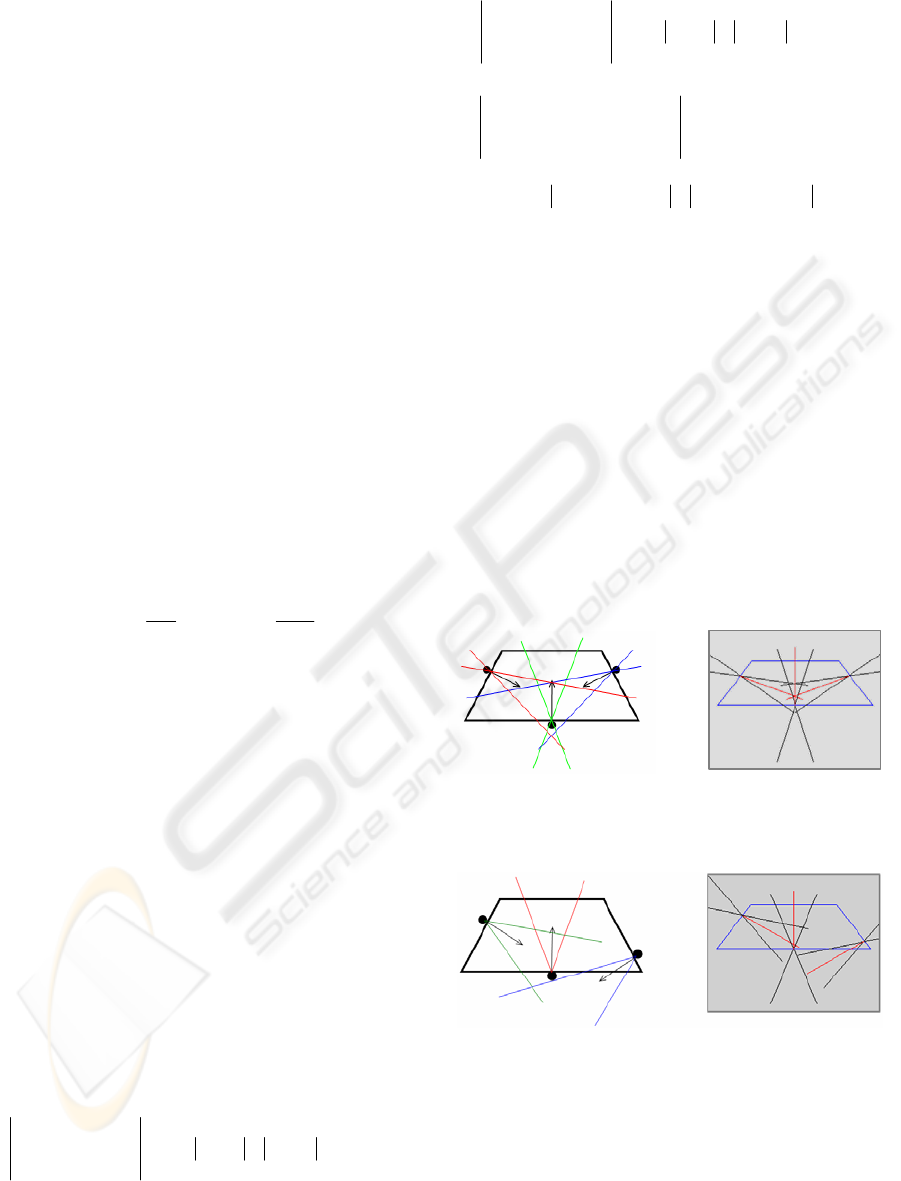
A second example is shown in figure 4; we

present a non-force-closure grasp using five contact

points. This grasp is instable and the object turn

around axis in the gray region (figure 4-a).

Figure 4: a) non-force-closure five-fingers grasp;

b) central axes of grasp wrenches ( ).

When a grasp is force closure, the central axes of

grasp wrenches can wholly sweep the plan . In

the third example, shown in figure 5, we use the

same finger’s configuration as figure 3 but we

change the friction angle . The grasp

becomes force-closure.

(

YX,

°= 20α

Figure 5: a) three fingers force-closure 2D grasp,

b) central axes of grasp wrenches ( ).

°= 20α

According to these three examples, we can

conclude that the distribution of central axes can

confirm if a grasp is force-closure or not (for any

contact points number).

4 FORCE-CLOSURE AND

EQUILIBRIUM CONDITION

In 2D grasps and based on Poinsot’s theorem, we

can give the following definition.

+Torque

(a)

(b)

Definition 1: Any external wrench applied by the

robotic hand on a 2D object is equivalent to a force

along a central axis of this wrench. When the force

is equal to zero, the external wrench is equivalent to

a torque about the grasp plan normal.

Definition 2: A grasp on an object is force-closure

if and only if any arbitrary force and torque can be

exerted on the object through the finger contacts

(Yan-Bin Jia 2004). There are other force-closure

definitions, but this one is more useful for our

deduction.

Definition 3: A grasp is said to achieve

equilibrium when it exists forces (not all of them

being zero) in the friction cones at the fingertips

ON COMPUTING MULTI-FINGER FORCE-CLOSURE GRASPS OF 2D OBJECTS

255

o/t

U =

o/c

UU =−=

U =

such that the sum of the corresonding wrenches is

zero (Sudsang A., Phoka T. 2005).

4.1 Equilibrium Condition

During objects grasp operations there exist two

kinds of external wrenches applied on the

manipulated object, task wrench (applied by the

environment) and contact wrench (applied by the

robotic hand fingers). Based on definitions 1 and

definitions 3, we derive a new proposed necessary

and sufficient equilibrium condition.

Proposition 1: A multifingers grasp is said to

achieve equilibrium if and only if the central lines of

contact wrench and task wrench have the same

support and opposite direction.

Proof:

i) Sufficient Condition:

the external contact wrench given by equation (5)

and task wrench is given by

⎥

⎦

⎤

⎢

⎣

⎡

o/t

(11)

U =

The object is in equilibrium if:

{}

⎩

⎨

⎧

−=

⇒=+

o/to/c

ττ

0WW

(12)

From Relation (9), the central axis of contact

wrench is defined by

o/cc

λ F

τF

OP +

(

(13)

o/t

o/c

λ U

⋅=

⎟

⎠

⎞

⎜

⎝

⎛

)

ℜ∈

Substuting (12) in (13) lead to

o/tt

λ F

τF

OP +

(14)

()

ℜ−= ∈

λλ

Relation (14) defines the central axis of task

wrench given by

o/tt

λ F

τF

OP +

(

(15)

)

ℜ∈

In the case , the points are given by

0F =

t c

o/tto/ccc

λλ ττOP ==

()

ℜ

−= ∈

λλ

(16)

In both cases, Relations (14) and (16), the two

wrenches (contact and task) should have the same

central line with opposite directions. ■

ii) Necessary Condition:

Now, if we consider two wrenches reduced at the

same point

O and they have the same central line

with opposite directions. We have two cases:

a) if

then the central axis of the task wrench is

defined by the unit vector where:

If the two wrenches have the same central line

with opposite direction then the contact central axis

is defined by the following unit vector:

We conclude that:

(

)

(

)

0<⋅

⋅

co/tco/c

SgnSgn UτUτ

(17)

Sgn is the sign function that computes the sign of

the leading coefficient of expression.

b) if , having the same central axis with

opposite direction implies

0F ≠

(

)

(

)

0<⋅

⋅

ctcc

SgnSgn UFUF

(18)

Where

and

define the unit vectors of the two

central axes. We have:

U U

;

Using hypothesis that there is one central line and

form relation (9), we have

o/tt

o/cc

τF

τF ×

(19)

Then, replacing

ccc

UFF =

;

ctt

UFF −=

Relation (19) we obtain

: (20)

(

ℜ∈λ

)

In 2D case, the equation (20) can be only

satisfied when

λ . therefore, the two torques have

opposite signes:

(

)

(

)

0<⋅

⋅

ZτZτ

o/to/c

SgnSgn

(21)

Relations (17, 18 and 21) imply that the contact

wrench can generate grasp wrenches that opposite

the external task wrench. Robotic hand can control

its fingers force to produce the appropriate

force/torque magnitude that achieving equilibrium.■

4.2 Force-Closure Condition

In particular, force-closure implies equilibrium, but

there are wrench systems that achieve equilibrium

but not force closure (Li Jia-Wei. and Cia He-Gao,

2003).

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

256

Using force-closure condition in definition 2, we

can derive this definition

Using force-closure condition in definition 2, we

can derive this definition

Definition 4: A grasp is force closed, if and only if

it is in equilibrium for any arbitrary wrench (Bicchi

A., Kumar V. 2000, Nguyen, V.D. 1988). Thus,

force closure implies, fingers contact wrenches can

balance any external task wrenches.

Definition 4: A grasp is force closed, if and only if

it is in equilibrium for any arbitrary wrench (Bicchi

A., Kumar V. 2000, Nguyen, V.D. 1988). Thus,

force closure implies, fingers contact wrenches can

balance any external task wrenches.

According to proposition 1 and definition 4, we

propose a new force-closure necessary and sufficient

condition.

According to proposition 1 and definition 4, we

propose a new force-closure necessary and sufficient

condition.

Proposition 2: A multifingred grasp of 2D objects

is said to achieve force-closure if and only if the

central axis of the fingers contact wrenches can

sweep the grasp plan at any direction.

Proposition 2: A multifingred grasp of 2D objects

is said to achieve force-closure if and only if the

central axis of the fingers contact wrenches can

sweep the grasp plan at any direction.

4.3 Force-Closure Test Algorithm 4.3 Force-Closure Test Algorithm

According to the proposition 2, we present a new

algorithm for computing 2D multi-fingers grasps of

arbitrary object.

According to the proposition 2, we present a new

algorithm for computing 2D multi-fingers grasps of

arbitrary object.

Based on the central axis equation defined in

relation (10), this central line can sweep the plan in

all directions if

Based on the central axis equation defined in

relation (10), this central line can sweep the plan in

all directions if

()

,k,k Δ

∃ℜ∈∀

Satisfy Satisfy

kxky

(a) (b)

(a)

(b)

()

,k,k Δ

∃ℜ∈∀

kxky

⋅=

Where

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

o/z

In other word, for any axis on the plan or

along the vertical , this axis must be one of the

grasp wrench central axes.

(

YX,

)

This condition implies that the quantities and

must take all real number, therefore

[]

⎪

⎩

⎪

⎨

⎧

∀+∞∞−∈

+∞∞−∈

O,τ

o/c

(21)

The third sub-condition is function of the reduced

point of the torque, to cover the entire grasp plan; we

test this condition at all the vertices of the

intersection of the m double-side friction cones

(named ). In general case of m contact points, the

number of intersection points is given by

(

∑

−

−⋅=

kmN

)

(22)

Hence, a multifingred 2D grasp is said to achieve

force-closure if each of these inequalities are true.

()

∑∑

⋅+⋅<+⋅

nXnXnnX (23-1)

()

∑∑

⋅+⋅<+⋅

nYnYnnY (23-2)

()()

()

∑

∧⋅+∧⋅

<+∧⋅

iikiik

iiik

nCBZnCBZ

nnCBZ

(23-3)

From mechanical viewpoint, inequality (23-1)

implies that fingers can generate forces

along and

X X

−

, (23-2) means that fingers can exert

force on the object along and . If the last

inequality (23-3) is true

Y Y−

(

)

N...kfor 1=

then the

finger can exert torque on object about the vertical

axis in both directions.

5 EXAMPLES

We present bellow some grasp examples using three,

four and five fingers. In both cases (force-closure

and no force-closure), we show the distribution of

grasp wrench central axes.

a) Three-finger grasps

Figure 6: a) a three-finger force-closure 2D grasp, b)

central axes of grasp wrenches ( ).

°=15α

Figure 7: a) a three-finger force-closure 2D grasp, b)

central axes of grasp wrenches ( ).

°= 20α

ON COMPUTING MULTI-FINGER FORCE-CLOSURE GRASPS OF 2D OBJECTS

257

(a)

(b)

Figure 8: a) no force-closure 2D grasp, b) central axes of

grasp wrenches (

). Grasp wrenches can’t generate

a negative torque in grey zone.

(a)

(b)

(a)

(b)

(a)

(b)

°=10

)

Figure 9: a) no force-closure 2D grasp, b) central axes of

grasp wrenches (

).Grasp wrenches can’t exert a

force along

(

axis and can’t generate torques in two-

direction in unreachable zones in (b).

°=10

Y−

b) Four-finger grasps

Figure 10: a) four-finger force-closure 2D grasp, b) central

axes of grasp wrenches ( ).

°=10α

c) Five-finger grasps

Figure 11: a) five-finger force-closure 2D grasp, b) central

axes of grasp wrenches ( ).

°= 25α

6 CONCLUSION AND FUTURE

WORK

We have presented a new equilibrium and force-

closure conditions for multifingred 2D grasps. A

novel algorithm for computing 2D multi-finger

force-closure grasps of arbitrary objects was

developed, which is very simple and needs little

geometric computations. Therefore, it can be

implemented in real-time multifingred grasp

programming. Our future work will be concentrated

on the extending of this algorithm to the 3D grasps

and the quality measurement of grasps.

REFERENCES

Bicchi A., Kumar V. (2000). Robotic grasping and

Contact: A review. In

Proc. IEEE ICRA, pp. 348–352.

Ding D., Liu Y-H, and S. Wang (2001). Computation of 3-

d form-closure grasps. In

IEEE Transactions on

Robotics and Automation

, 515-522.

Li J-W., Cia He-Gao (2003). On Computing Three-Finger

Force-Closure Grasps of 2-D and 3-D Objects.

Transaction on Robotics & Automation. IEEE

Proceeding, 155-161.

Li J-W., Jin M-H., Liu H. (2003). A New Algorithm for

Three-finger Force-Closure Grasp of Polygonal

Objects. In

International Conference on Robotics &

Automation.

IEEE Proceeding, 1800-1804.

Murray R., Li Z., Sastry S. (1994).

A Mathematical

Introduction to Robotic Manipulation,

Boca Raton,

FL: CRC press.

Nguyen, V.D. (1988). Constructing force-closure grasps.

Journal of Robotics Research, vol. 7, no. 3, pp. 3-

16.

Ponce J. and Faverjon B.. (1995). On computing three-

finger force-closure grasps of polygonal objects. In

IEEE Transactions on Robotics and Automation, 868-

881.

Salisbury J.K. and Roth B. (1982) Kinematic and force

analysis of articulated hands

. In Journal of

Mechanisms, Transmissions, and Automation in

Design,

105, 33-41.

Sudsang A., Phoka T. (2005). Geometric Reformulation of

3-Fingred Force-Closure Condition. In

International

Conference on Robotics & Automation.

IEEE

Proceeding, 2338-2343.

Yan-Bin Jia (2004). Computation on Parametric Curves

with an Application in Grasping. In

the International

Journal of Robotics Research,

vol. 23, No. 7-8, 825-

855.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

258