DC MOTOR FAULT DIAGNOSIS BY MEANS OF ARTIFICIAL

NEURAL NETWORKS

Krzysztof Patan, J

ozef Korbicz and Gracjan Głowacki

Institute of Control and Computation Engineering, University of Zielona G

ora

ul. Podg

orna 50, 65-246 Zielona G

ora, Poland

Keywords:

Neural networks, DC motor, modelling, density shaping, fault detection, fault isolation, fault identiﬁcation.

Abstract:

The paper deals with a model-based fault diagnosis for a DC motor realized using artiﬁcial neural networks.

The considered process was modelled by using a neural network composed of dynamic neuron models. De-

cision making about possible faults was performed using statistical analysis of a residual. A neural network

was applied to density shaping of a residual, and after that, assuming a signiﬁcance level, a threshold was

calculated. Moreover, to isolate faults a neural classiﬁer was developed. The proposed approach was tested in

a DC motor laboratory system at the nominal operating conditions as well as in the case of faults.

1 INTRODUCTION

Electrical motors play a very important role in the

safe and efﬁcient work of modern industrial plants

and processes. An early diagnosis of abnormal and

faulty states renders it possible to perform important

preventing actions and it allows one to avoid heavy

economic losses involved in stopped production, re-

placement of elements or parts (Patton et al., 2000).

To keep an electrical machine in the best condition, a

several techniques like fault monitoring or diagnosis

should be implemented. Conventional DC motors are

very popular, because they are reasonably cheap and

easy to control. Unfortunately, their main drawback

is the mechanical collector which has only a limited

life spam. In addition, brush sparking can destroy the

rotor coil, generate EMC problems and reduce the in-

sulation resistance to an unacceptable limit (Moseler

and Isermann, 2000). Moreover, in many cases elec-

trical motors operate in the closed-loop control, and

small faults often remain hidden by the control loop.

Only if the whole device fails the failure becomes vis-

ible. Therefore, there is a need to detect and isolate

faults as early as possible.

Recently, a great deal of attention has been paid

to electrical motor fault diagnosis (Moseler and Is-

ermann, 2000; Xiang-Qun and Zhang, 2000; Fues-

sel and Isermann, 2000). In general, elaborated solu-

tions can be splitted into three categories: signal anal-

ysis methods, knowledge-based methods and model-

based approaches (Xiang-Qun and Zhang, 2000; Ko-

rbicz et al., 2004). Methods based on signal anal-

ysis include vibration analysis, current analysis, etc.

The main advantage of these approaches is that accu-

rate modelling of a motor is avoided. However, these

methods only use output signals of a motor, hence the

inﬂuence of an input on an output is not considered.

In turn, the frequency analysis is time-consuming,

thus it is not proper for on-line fault diagnosis. In the

case of vibration analysis there are serious problems

with noise produced by environment and coupling of

sensors to the motor (Xiang-Qun and Zhang, 2000).

Knowledge-based approaches are generally based

on expert or qualitative reasoning (Zhang and Ellis,

1991). Several knowledge based fault diagnosis ap-

proaches have been proposed. These include the rule-

based approaches where diagnostic rules can be for-

mulated from process structure and unit functions,

and the qualitative simulation-based approaches. The

trouble with the use of such models is that accumulat-

ing experience and expressing it as knowledge rules

is difﬁcult and time-consuming. Therefore, develop-

ment of a knowledge-based diagnosis system is gen-

erally effort demanding.

Model-based approaches include parameter esti-

mation, state estimation, etc. This kind of methods

can be effectively used to on-line diagnosis, but its

disadvantage is that an accurate model of a motor is

required (Korbicz et al., 2004). An alternative so-

lution can be obtained through artiﬁcial intelligence,

e.g. neural networks. The self-learning ability and

property of modelling nonlinear systems allow one to

employ neural networks to model complex, unknown

and nonlinear dynamic processes (Frank and K

oppen-

Patan K., Korbicz J. and Głowacki G. (2007).

DC MOTOR FAULT DIAGNOSIS BY MEANS OF ARTIFICIAL NEURAL NETWORKS.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 11-18

DOI: 10.5220/0001625400110018

 SciTePress

Seliger, 1997).

The paper is organized as follows. First, descrip-

tion of the considered DC motor is presented in Sec-

tion 2. The model-based fault diagnosis concept is

discussed in Section 3. The architecture details of the

dynamic neural network used as a model of the DC

motor is given in Section 4. Next, a density shaping

technique used to fault detection and a neural classi-

ﬁer applied to isolation of faults are explained in Sec-

tion 5. Section 6 reports experimental results.

2 AMIRA DR300 LABORATORY

SYSTEM

The AMIRA DR300 laboratory system shown in

Fig. 1 is used to control the rotational speed of a DC

motor with a changing load. The considered labora-

tory object consists of ﬁve main elements: the DC

motor M1, the DC motor M2, two digital increamen-

tal encoders and the clutch K. The input signal of the

engine M1 is an armature current and the output one

is the angular velocity. Available sensors for the out-

put are an analog tachometer on optical sensor, which

generates impulses that correspond to the rotations of

the engine and a digital incremental encoder. The

shaft of the motor M1 is connected with the identical

motor M2 by the clutch K. The second motor M2 op-

erates in the generator mode and its input signal is an

armature current. Available measuremets of the plant

are as follows:

• motor current I

– the motor current of the DC

motor M1,

• generator current I

– the motor current of the DC

motor M2,

• tachometer signal T ,

and control signals:

• motor control signal C

– the input of the motor

M1,

Figure 1: Laboratory system with a DC motor.

Table 1: Laboratory system technical data.

Variable Value

Motor

rated voltage 24 V

rated current 2 A

rated torque 0.096 Nm

rated speed 3000 rpm

voltage constant 6.27 mV/rpm

moment of inertia 17.7 × 10

−6

Kgm

torque constant 0.06 Nm/A

resistance 3.13 Ω

Tachometer

output voltage 5 mV/rpm

moment of interia 10.6 × 10

−6

Kgm

Clutch

moment of inertia 33 × 10

−6

Kgm

Incremental encoder

number of lines 1024

max. resolution 4096/R

moment of inertia 1.45 × 10

−6

Kgm

• generator control signal C

– the input of the mo-

tor M2.

The technical data of the laboratory system is pre-

sented in Table 1. The separately excited DC motor is

governed by two differential equations. The electrical

subsystem can be described by the equation:

u(t) = Ri(t) + L

di(t)

+ e(t) (1)

where u(t) is the motor armature voltage, R – the ar-

mature coil resistance, i(t) – the motor armature cur-

rent, L – the motor coil inductance, and e(t) – the

induced electromotive force. The induced electromo-

tive force is proportional to the angular velocity of the

motor: e(t) = K

ω(t), where K

stands for the motor

voltage constant and ω(t) – the angular velocity of

the motor. In turn, the mechanical subsystem can be

derived from the torque balance:

dω(t)

= T

(t) − B

ω(t) − T

− T

(ω(t)) (2)

where J is the motor moment of inertia, T

– the mo-

tor torque, B

– the viscous friction torque coefﬁ-

cient, T

– the load torque, and T

(ω(t)) – the friction

torque. The motor torque T

(t) is proportional to the

armature current: T

(t) = K

i(t), where K

stands

for the motor torque constant. The friction torque

can be considered as a function of angular velocity

and it is assumed to be the sum of Stribeck, Coulumb

and viscous components. The viscous friction torque

opposes motion and it is proportional to the angular

velocity. The Coulomb friction torque is constant at

any angular velocity. The Stribeck friction is a non-

linear component occuring at low angular velocities.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

The model (1)-(2) has a direct relation to the motor

physical parameters, however, the relation between

them is nonlinear.There are many nonlinear factors in

the motor, e.g. the nonlinearity of the magnetization

chracteristic of material, the effect of material reac-

tion, the effect caused by eddy current in the mag-

net, the residual magnetism, the commutator charac-

teristic, mechanical frictions (Xiang-Qun and Zhang,

2000). Summarizing, a DC motor is a nonlinear dy-

namic process.

3 MODEL-BASED FAULT

DIAGNOSIS

Model-based approaches generally utilise results

from the ﬁeld of control theory and are based on pa-

rameter estimation or state estimation (Patton et al.,

2000; Korbicz et al., 2004). When using this ap-

proach, it is essential to have quite accurate models of

a process. Generally, fault diagnosis procedure con-

sists of two separate stages: residual generation and

residual evaluation. The residual generation process

is based on a comparison between the output of the

system and the output of the constructed model. As

a result, the difference or so-called residual r is ex-

pected to be near zero under normal operating con-

ditions, but on the occurrence of a fault, a deviation

from zero should appear. Unfortunately, designing

mathematical models for complex nonlinear systems

can be difﬁcult or even impossible. For the model-

based approach, the neural network replaces the an-

alytical model that describes the process under nor-

mal operating conditions (Frank and K

oppen-Seliger,

1997). First, the network has to be trained for this

task. Learning data can be collected directly from the

process, if possible or from a simulation model that is

as realistic as possible. Training process can be car-

ried out off-line or on-line (it depends on availability

of data). After ﬁnishing the training, a neural network

is ready for on-line residual generation. In order to

be able to capture dynamic behaviour of the system, a

neural network should have dynamic properties, e.g.

it should be a recurrent network (Korbicz et al., 2004;

Patan and Parisini, 2005). In turn, the residual evalua-

tion block transforms the residual r into the fault vec-

tor f in order to determine the decision about faults,

their location and size, and time of fault occurence.

In general, there are three phases in the diagnos-

tic process: detection, isolation and identiﬁcation of

faults (Patton et al., 2000; Korbicz et al., 2004). In

practice, however, the identiﬁcation phase appears

rarely and sometimes it is incorporated into fault iso-

lation. Thus, from practical point of view, the diag-

nostic process consists of two phases only: fault de-

tection and isolation. The main objective of fault de-

tection is to make a decision whether a fault occur

or not. The fault isolation should give an information

about fault location. Neural networks can be very use-

full in designing the residual evaluation block. In the

following sections some solutions for realization fault

detection and isolation are discussed.

4 DYNAMIC NEURAL NETWORK

Let us consider the neural network described by the

following formulae:

(k) =

∑

i=1

(k) (3)

(k) =

∑

i=0

(k − i) −

∑

i=1

(k − i) (4)

(k) = f (z

(k)) (5)

(k) =

∑

i=1

(k) +

∑

i=1

(k) (6)

(k) = −

∑

i=1

(k − i) (7)

(k) =

∑

i=1

(k) (8)

where w

, j = 1,..., v

are the input weights, w

j = 1, .. .,v

– the weights between the output and the

ﬁrst hidden layers, w

, j = 1, ... ,m – the weights be-

tween the output and the second hidden layers, w

j = 1, ... ,v

– the weights between output and input

layers, ϕ

(k) and ϕ

(k) are the weighted sums of in-

puts of the j-th neuron in the hidden and output lay-

ers, respectively, u

(k) are the external inputs to the

network, z

(k) is the activation of the j-th neuron in

the ﬁrst hidden layer, a

and a

are feedback ﬁlter

parameters of the j-th neuron in the ﬁrst and second

hidden layers, respectively, b

are the feed-forward

ﬁlter parameters of the j-th neuron of the ﬁrst hidden

layer, f (·) – nonlinear activation function, y

(k) and

(k) – the outputs of the j-th neuron of the ﬁrst and

second hidden layers, respectively, and ﬁnally y

(k),

j = 1, ... ,v

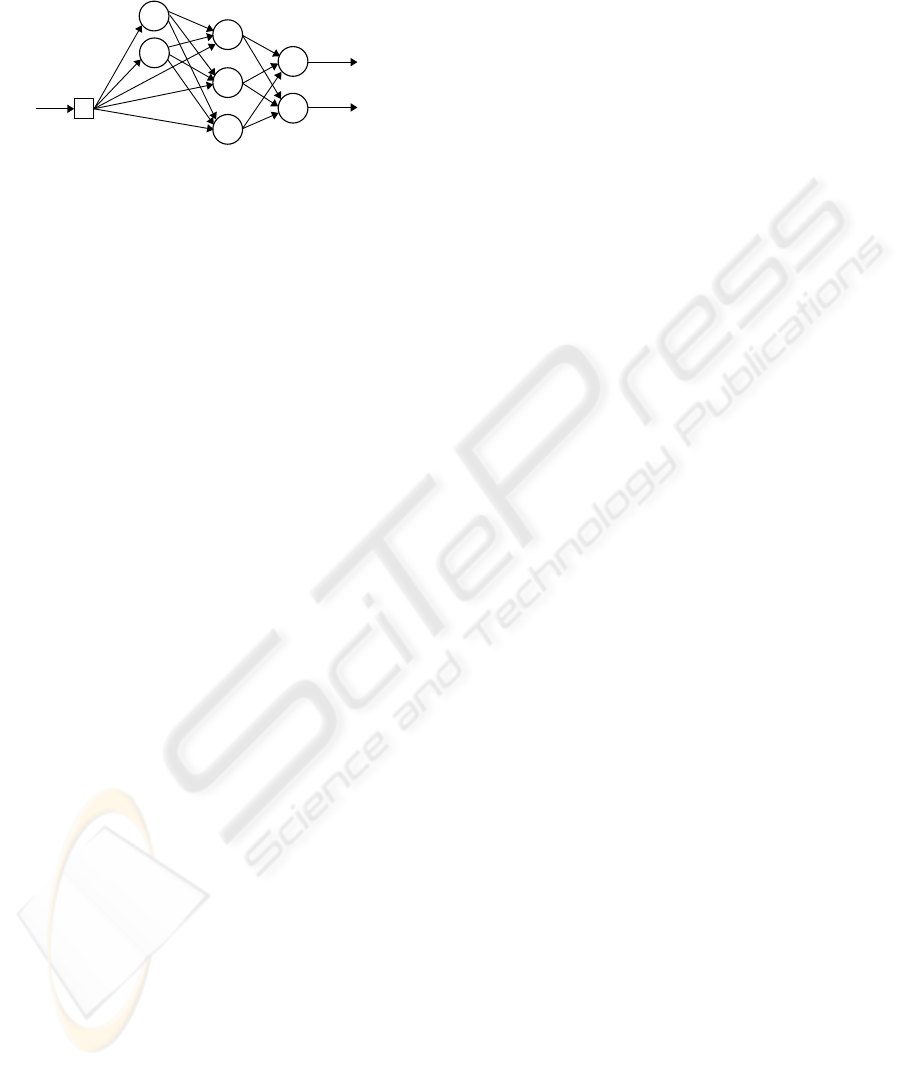
are the network ouputs. The structure

of the network is presented in Fig. 2. The ﬁrst hid-

den layer consists of v

neurons with inﬁnite impulse

response ﬁlters of the order r

and nonlinear activa-

tion functions. The second hidden layer consists of

neurons with ﬁnite impulse response ﬁlters of the

order r

and linear activation functions. Neurons of

this layer receive excitation not only from the neu-

DC MOTOR FAULT DIAGNOSIS BY MEANS OF ARTIFICIAL NEURAL NETWORKS

IIR – neuron with IIR ﬁlter

FIR – neuron with FIR ﬁlter

L – static linear neuron

u(k)

(k)

FIR

IIR

Figure 2: The cascade structure of the dynamic neural net-

work.

rons of the hidden layer but also from the external in-

puts (Fig. 2). Finaly, the network output is produced

by the linear output layer. The network structure (3)-

(8) is not a strict feed-forward one. It has a cascade

structure. Detailed analysis of this network and its ap-

proximation abilities are given in paper (Patan, 2007).

Introduction of an additional weight matrix W

ren-

ders it possible to obtain a system, in which the whole

state vector is available from the neurons of the out-

put layer. In this way, the proposed neural model can

produce a state vector at its output and can serve as

a nonlinear observer. This fact is of a crucial impor-

tance taking into account training of the neural net-

work. Moreover, this neural structure has similar ap-

proximation abilities as a locally recurrent globally

feedforward network with two hidden layers designed

using nonlinear neuron models with IIR ﬁlters, while

the number of adaptable parameters is signiﬁcantly

lower (Patan, 2007).

4.1 Network Training

All unknown network parameters can be represented

by a vector θ. The objective of training is to ﬁnd the

optimal vector of parameters θ

by minimization of

some loss (cost) function:

= arg

θ∈C

min J(θ) (9)

where J : R

→ R represents some loss function to be

minimized, p is the dimension of the vector θ, and

C ⊆ R

is the set of admissible parameters consti-

tuted by constraints. To minimize (9) one can use the

Adaptive Random Search algorithm (ARS) (Walter

and Pronzato, 1996). Assuming that the sequence of

solutions

,.. .,

is already appointed, the next

point

k+1

is calculated as follows (Walter and Pron-

zato, 1996):

k+1

+ r

(10)

where

is the estimate of the θ

at the k-th itera-

tion, and r

is the perturbation vector generated ran-

domly according to the normal distribution N (0,σ).

The new point

k+1

is accepted when the cost func-

tion J(

k+1

) is lower than J(

) otherwise

k+1

To start the optimization procedure, it is necessary to

determine the initial point

and the variance σ. Let

be a global minimum to be located. When

is far

from θ

, r

should have a large variance to allow large

displacements, which are necessary to escape the lo-

cal minima. On the other hand, when

is close θ

should have a small variance to allow exact explo-

ration of parameter space. The idea of the ARS is to

alternate two phases: variance-selection and variance-

exploitation (Walter and Pronzato, 1996). During the

variance-selection phase, several successive values of

σ are tried for a given number of iteration of the basic

algorithm. The competing σ

is rated by their perfor-

mance in the basic algorithm in terms of cost reduc-

tion starting from the same initial point. Each σ

computed according to the formula:

= 10

−i

, for i = 1, ... ,4 (11)

and it is allowed for 100/i iterations to give more

trails to larger variances. σ

is the initial variance and

can be determined, e.g. as a spread of the parameters

domain:

= θ

max

− θ

min

(12)

where θ

max

and θ

min

are the largest and lowest pos-

sible values of parameters, respectively. The best σ

in terms the lowest value of the cost function is se-

lected for the variance-exploitation phase. The best

parameter set

and the variance σ

are used in the

variance-exploitation phase, whilst the algorithm (10)

is run typically for one hundred iterations. The algo-

rithm can be terminated when the maximum number

of algorithm iteration n

max

is reached or when the as-

sumed accuracy J

min

is obtained. Taking into account

local minima, the algorithm can be stopped when σ

has been selected a given number of times. It means

that algorithm got stuck in a local minimum and can-

not escape its basin of attraction. Apart from its sim-

plicity, the algorithm possesses the property of global

convergence. Moreover, adaptive parameters of the

algorithm, cause that a chance to get stuck in local

minima is decreased.

5 NEURAL NETWORKS BASED

DECISION MAKING

5.1 Fault Detection

In many cases, the residual evaluation is based on the

assumption that the underlying data is normally dis-

tributed (Walter and Pronzato, 1996). This weak as-

sumption can cause inaccurate decision making and a

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

number of false alarms can be considerable. Thus,

in order to select a threshold in a proper way, the

distribution of the residual should be discovered or

transformation of the residual to another known dis-

tribution should be performed. A transformation of a

random vector x of an arbitrary distribution to a new

random vector y of different distribution can be re-

alized by maximazing the output entropy of the neu-

ral network (Haykin, 1999; Roth and Baram, 1996;

Bell and Sejnowski, 1995). Let us consider a situ-

ation when a single input is passed through a trans-

forming function f (x) to give an output y, where f (x)

is monotonically increasing continuous function sat-

isfying lim

x→+∞

f (x) = 1 and lim

x→−∞

f (x) = 0. The

probability density function of y satisﬁes

(y) =

(x)

|∂y/∂x|

(13)

The entropy of the output h(y) is given by

h(y) = −E{log p

(y)} (14)

where E{·} stands for the expected value. Substitut-

ing (13) into (14) it gives

h(y) = h(x) + E



log



∂y

∂x





(15)

The ﬁrst term on the right can be considered to be un-

affected by alternations in parameters of f (x). There-

fore, to maximize the entropy of y one need to take

into account the second term only.

Let us deﬁne the divergence between two density

functions as follows

D(p

(x),q

(x)) = E



log

(x)



(16)

ﬁnally one obtains

h(y) = −D(p

(x),q

(x)) (17)

where q

(x) = |∂(y)/∂(x)|. The divergence between

true density of x (p

(x)) and an arbitrary one q

(x) is

minimized when entropy of y is maximized. The in-

put probability density function is then approximated

by |∂y/∂x|. The simple and elegant way to adjust net-

work parameters in order to maximize the entropy of

y was given in (Bell and Sejnowski, 1995). They used

the on-line version of stochastic gradient ascent rule

∆w=

∂h(y)

∂w

∂

∂w



log



∂y

∂x







∂y

∂x



−1

∂

∂w



∂y

∂x



(18)

Considering the logistic transfer function of the

form:

y =

1 + exp (−u)

, u = wx + b (19)

f (·)

− +

w +

ˆq(x)

x u

Figure 3: Neural network for density calculation.

where w is the input weight and b is the bias weight,

and applying (18) to (19) ﬁnally one obtains

∆w =

+ x(1 + 2y) (20)

Using a similar reasoning, a rule for the bias weight

parameter can be derived

∆b = 1 − 2y (21)

After training, the estimated probability density func-

tion can be calculated using scheme shown in Fig. 3.

In this case, an output threshold of the density shap-

ing scheme (Fig. 3) can be easily calculated by the

formula:

= |0.5α(1 − 0.5α)w| (22)

where α is the conﬁdence level.

5.2 Fault Isolation

Transformation of the residual r into the fault vector

f can be seen as a classiﬁcation problem. For fault

isolation, it means that each pattern of the symptom

vector r is assigned to one of the classes of system be-

haviour { f

, f

,.. ., f

}. To perform fault isolation,

the well-known static multi-layer perceptron network

can be used. In fact, the neural classiﬁer should map

a relation of the form Ψ : R

→ R

: Ψ(r) = f.

5.3 Fault Identiﬁcation

When analytical equations of residuals are unknown,

the fault identiﬁcation consists in estimating the fault

size and time of fault occurence on the basis of resid-

ual values. An elementary index of the residual size

assigned to the fault size is the ratio of the residual

value r

to suitably assigned threshold value T

. This

threshold can be calculated using (22). In this way,

the fault size can be represented as the mean value of

such elementary indices for all residuals as follows:

s( f

) =

∑

j:r

∈R( f

)

(23)

where s( f

) represents the size of the fault f

, R( f

)

– the set of residuals sensitive to the fault f

, N – the

size of the set R( f

DC MOTOR FAULT DIAGNOSIS BY MEANS OF ARTIFICIAL NEURAL NETWORKS

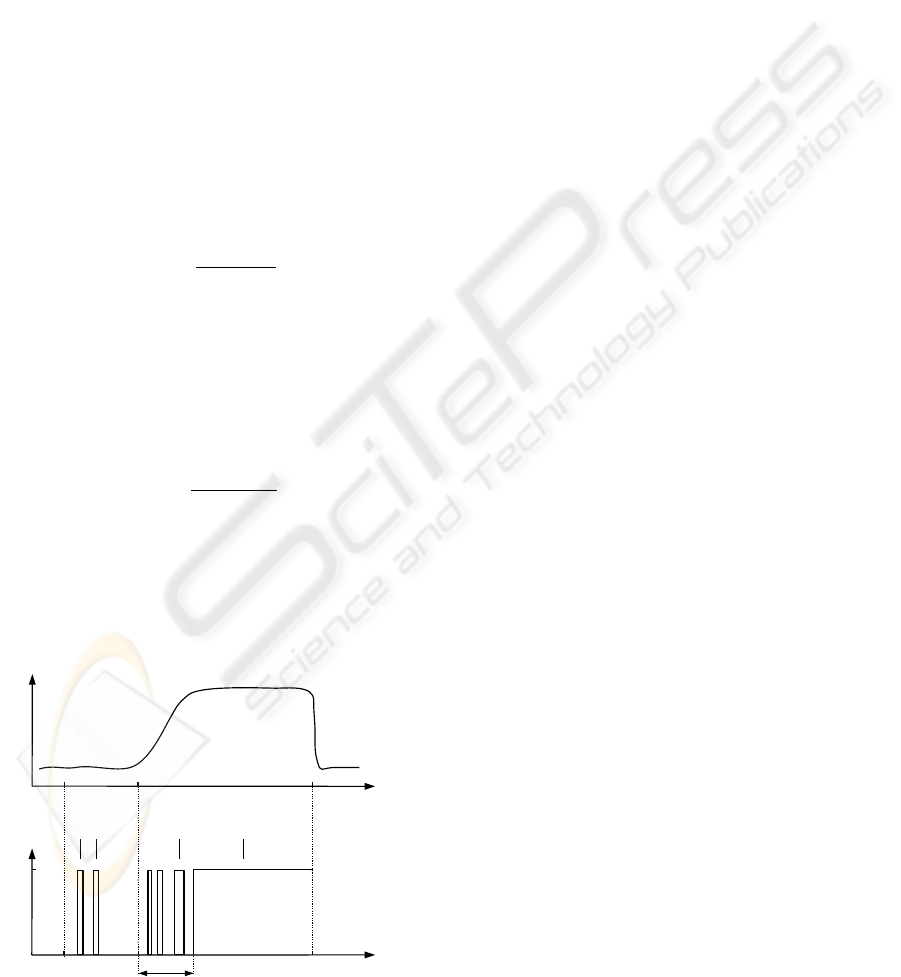
5.4 Evaluation of the Fdi System

The benchmark zone is deﬁned from the benchmark

start-up time t

to the benchmark time horizon t

hor

(Fig. 4). Decisions before the benchmark start-up t

and after the benchmark time horizon t

hor

are out of

interest. The time of fault start-up is represented by

f rom

. When a fault occurs in the system, a residual

should deviate from the level assigned to the fault-free

case (Fig. 4). The quality of the fault detection sys-

tem can be evaluated using a number of performance

indexes (Patan and Parisini, 2005):

• Time of fault detection t

– a period of time

needed for detection of a fault measured from

f rom

to a permanent, true decision about a fault,

as presented in Fig. 4. As one can see there, the

ﬁrst three true decisions are temporary ones and

are not taken into account during determining t

• False detection rate r

f d

∑

f d

f rom

−t

, (24)

where t

f d

is the period of i-th false fault detection.

This index is used to check the system in the fault-

free case. Its value shows a percentage of false

alarms. In the ideal case (no false alarms) its value

should be equal to 0.

• True detection rate r

∑

hor

−t

f rom

, (25)

where t

is the period of i-th true fault detection.

This index is used in the case of faults and de-

scribes efﬁciency of fault detection. In the ideal

case (fault detected immediately and surely) its

value is equal to 1.

f rom

hor

time

residualfault decision

true decisions

false

decisions

 ? ???

Figure 4: Illustration of performance indexes.

6 EXPERIMENTS

The motor described in Section 2 works is a closed

loop control with the PI controller. It is assumed that

load of the motor is equal to 0. The objective of the

system control is to keep the rotational speed at the

constant value equal to 2000. Additionally, it is as-

sumed that the reference value is corrupted by addi-

tive noise.

6.1 Motor Modelling

A separately excited DC motor was modelled by us-

ing dynamic neural network presented in Section 4.

The model of the motor was selected as follows:

T = f (C

) (26)

The following input signal was used in experiments:

(k) = 3 sin(2π0.017k) + 3sin(2π0.011k − π/7)

+ 3 sin(2π0.003k + π/3)

(27)

The input signal (27) is persistantly exciting of the or-

der 6. Using (27) a learning set containig 1000 sam-

ples was formed. The neural network model (3)-(8)

had the following structure: one input, 3 IIR neurons

with the ﬁrst order ﬁlters and hyperbolic tangent ac-

tivation functions, 6 FIR neurons with the ﬁrst order

ﬁlters and linear activation functions, and one linear

output neuron. Training process was carried out for

100 steps using the ARS algorithm with initial vari-

ance σ

= 0.1. The outputs of the neural model and

separately excited motor generated for another 1000

testing samples are depicted in Fig. 5. The efﬁciency

of the neural model was also checked during the work

of the motor in the closed-loop control. The results

are presented in Fig. 6. After transitional oscilations,

the neural model settled at a proper value. This gives

a strong argument that neural model mimics the be-

haviour of the DC motor pretty well.

6.2 Fault Detection

Two types of faults were examined during experi-

ments:

• f

– tachometer faults were simulated by increas-

ing/decreasing rotational speed by ±25%, ±10%

and ±5%,

• f

– mechanical faults were simulated by increas-

ing/decreasing motor torque by ±40%, ±20%.

In result, a total of 10 faulty situation were investi-

gated. Using the neural model of the process, a resid-

ual signal was generated. This signal was used to

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

0 100 200 300 400 500 600 700 800 900 1000

−4000

−2000

2000

4000

time

rotational speed

Figure 5: Responses of the motor (solid) and neural model

(dash-dot) – open-loop control.

0 200 400 600 800 1000 1200 1400 1600 1800 2000

1000

2000

3000

4000

5000

time

rotational speed

Figure 6: Responses of the motor (solid) and neural model

(dash-dot) – closed-loop control.

train another neural network to approximate a prob-

ability density function of the residual. Training pro-

cess was carried out on-line for 100000 steps using

unsupervised learning described in Section 5.1. The

ﬁnal network parameters were: w = −711,43 and

b = −1.26. Cut off values determined for signiﬁcance

Table 2: Performance indices.

Fault r

R [%] s

0.9995 2035 99 19.51

0.9995 2000 82 12.60

0.9988 2097 56 5.78

0.9395 2086 84 5.45

0.9923 2142 62 4.07

0.5245 undetected 54 1.48

0.9998 2005 100 52.69

1.0 2000 100 29,24

0.9997 2005 96 27.30

0.9993 2008 97 14.56

level α = 0.05 had values x

= −0.007 and x

= 0,003

and the threshold was equal to T = 17, 341. In order

to perform decision about faults, and to determine de-

tection time t

, a time window with the length n = 50

was used. If during the following n time steps the

residual exceeded the threshold then a fault was sig-

nalled. Application of time-window prevents the sit-

uation when a temporary true detection will signal a

fault (see Fig. 4). The results of fault detection are

presented in the second and third columns of Table 2.

All faults were reliably detected except fault f

. In

this case, the changes simulated on tachometer sensor

were poorly observed in the residual.

6.3 Fault Isolation

Fault isolation can be considered as a classiﬁcation

problem where a given residual value is assigned to

one of the predeﬁned classes of system behaviour. In

the case considered here, there is only one residual

signal and 10 different faulty scenarios. To perform

fault isolation the well-known multilayer perceptron

was used. The neural network had one input (residual

signal) and 4 outputs (each class of system behaviour

was coded using 4-bit representation). The learning

set was formed using 100 samples per each faulty

situation and 100 samples representing the fault-free

case, then the size of the learning set was equal to

1100. As the well performing neural classiﬁer, the

network with 15 hyperbolic tangent neurons in the

ﬁrst hidden layer, 7 hyperbolic tangent neurons in the

second hidden layer, and 4 sigmoidal output neurons

was selected. The neural classiﬁer was trained for 500

steps using the Levenberg-Marquardt method. Addi-

tionally, the real-valued response of the classiﬁer was

transformed to the binary one. The simple idea is to

calculate a distance between the classiﬁer output and

each predeﬁned class of system behaviour. As a re-

sult, a binary representation giving the shortest dis-

tance is selected as a classiﬁer binary output. This

transformation can be represented as follows:

j = arg min

||x − K

||, i = 1, ... ,N

(28)

where x is the real-valued output of the classiﬁer, K

–

the binary representation of the i-th class, N

– the

number of predeﬁned classes of system behaviour,

and || · || – the Euclidean distance. Then, the binary

representation of the classiﬁer can be determined in

the form ¯x = K

. Recognition accuracy (R) results are

presented in the fourth column of Table 2. The worst

results 56% and 62% were obtained for the faults f

and f

, respectively. The fault f

was frequently rec-

ognized as the fault f

. In spite of misrecognizing,

this fault was detected as a faulty situation. Quite dif-

ferent situation was observed for the classiﬁcation of

DC MOTOR FAULT DIAGNOSIS BY MEANS OF ARTIFICIAL NEURAL NETWORKS

fault f

. This fault, in majority of cases, was classi-

ﬁed as the normal operating conditions, thus it cannot

be either detected or isolated properly.

6.4 Fault Identiﬁcation

In this work, the objective of fault identiﬁcation was

to estimate the size of detected and isolated faults.

The sizes of faults were calculated using (23). The

results are shown in the last column of Table 2. Ana-

lyzing results, one can observe that quite large values

were obtained for the faults f

, f

and f

. That

is the reason that for these three faults true detection

rate and recognition accuracy had maximum or close

to maximum values. Another group is formed by the

faults f

, f

and f

possessing the similar values

of the fault size. The third group of fault consists of

, f

, and f

. The fault sizes in these cases are

distinctly smaller than in the cases already discussed.

Also the detection time t

is relatively longer. In spite

of the fact that f

was not detected, the size of this

fault was also calculated. As one can see the fault size

in this case is very small, what explains the problems

with its detection and isolation.

7 FINAL REMARKS

In the paper, the neural network based method for the

fault detection and isolation of faults in a DC motor

was proposed. Using the novel structure of dynamic

neural network, quite accurate model of the motor

was obtained what rendered it possible detection, iso-

lation or even identiﬁcation of faults. The approach

was successfully tested on a number of faulty scenar-

ios simulated in the real plant. The achieved results

conﬁrm usefullness and effectiveness of neural net-

works in designing fault detection and isolation sys-

tems. It should be pointed out that presented solution

can be easily applied to on-line fault diagnosis.

ACKNOWLEDGEMENTS

This work was supported in part by the Ministry of

Science and Higher Education in Poland under the

grant Artiﬁcial Neural Networks in Robust Diagnostic

Systems

G. Głowacki is a stypendist of the Integrated Re-

gional Operational Programme (Measure 2.6: Re-

gional innovation strategies and the transfer of knowl-

edge) co-ﬁnanced from the European Social Fund.

REFERENCES

Bell, A. J. and Sejnowski, T. J. (1995). An information-

maximization approach to blind separation and blind

deconvolution. Neural computation, 7:1129–1159.

Frank, P. M. and K

oppen-Seliger, B. (1997). New devel-

opments using AI in fault diagnosis. Artiﬁcial Intelli-

gence, 10(1):3–14.

Fuessel, D. and Isermann, R. (2000). Hierarchical motor

diagnosis utilising structural knowledge and a self-

learning neuro-fuzzy scheme. IEEE Trans. Industrial

Electronics, 47:1070–1077.

Haykin, S. (1999). Neural Networks. A comprehensive

foundation, 2nd Edition. Prentice-Hall, New Jersey.

Korbicz, J., Ko

scielny, J. M., Kowalczuk, Z., and Cholewa,

W., editors (2004). Fault Diagnosis. Models, Artiﬁcial

Intelligence, Applications. Springer-Verlag, Berlin.

Moseler, O. and Isermann, R. (2000). Application of model-

based fault detection to a brushless dc motor. IEEE

Trans. Industrial Electronics, 47:1015–1020.

Patan, K. (2007). Approximation ability of a class of locally

recurrent globally feedforward neural networks. In

Proc. European Control Conference, ECC 2007, Kos,

Greece. accepted.

Patan, K. and Parisini, T. (2005). Identiﬁcation of neural

dynamic models for fault detection and isolation: the

case of a real sugar evaporation process. Journal of

Process Control, 15:67–79.

Patton, R. J., Frank, P. M., and Clark, R. (2000). Issues

of Fault Diagnosis fo r Dynamic Systems. Springer-

Verlag, Berlin.

Roth, Z. and Baram, Y. (1996). Multidimensional density

shaping by sigmoids. IEEE Trans. Neural Networks,

7(5):1291–1298.

Walter, E. and Pronzato, L. (1996). Identiﬁcation of Para-

metric Models from Experimental Data. Springer,

London.

Xiang-Qun, L. and Zhang, H. Y. (2000). Fault detection

and diagnosis of permanent-magnet dc motor based

on parameter estimation and neural network. IEEE

Trans. Industrial Electronics, 47:1021–1030.

Zhang, J., P. D. R. and Ellis, J. E. (1991). A self-learning

fault diagnosis system. Transactions of the Institute of

Measurements and Control, 13:29–35.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics