
A CLOSED-FORM
MODEL PREDICTIVE CONTROL FRAMEWORK FOR
NONLINEAR NOISE-CORRUPTED SYSTEMS
Florian Weissel, Marco F. Huber and Uwe D. Hanebeck
Intelligent Sensor-Actuator-Systems Laboratory, Universit
¨
at Karlsruhe (TH), Germany
Keywords:
Nonlinear Model Predictive Control; Stochastic Systems; Nonlinear Estimation.
Abstract:
In this paper, a framework for Nonlinear Model Predictive Control (NMPC) that explicitly incorporates the
noise influence on systems with continuous state spaces is introduced. By the incorporation of noise, which
results from uncertainties during model identification and the measurement process, the quality of control
can be significantly increased. Since NMPC requires the prediction of system states over a certain horizon,
an efficient state prediction technique for nonlinear noise-affected systems is required. This is achieved by
using transition densities approximated by axis-aligned Gaussian mixtures together with methods to reduce
the computational burden. A versatile cost function representation also employing Gaussian mixtures provides
an increased freedom of modeling. Combining the prediction technique with this value function representation
allows closed-form calculation of the necessary optimization problems arising from NMPC. The capabilities
of the framework and especially the benefits that can be gained by considering the noise in the controller are
illustrated by the example of a mobile robot following a given path.
NOTATION
x variable
x
x
x random variable
x
x
x
vector-valued random variable
˜
f
x
(x) probability density function of x
x
x
f
x
(x) approximate of
˜
f
x
(x)
N (x−µ;σ
2
) Gaussian density with mean µ
and standard deviation σ
E
x
x
x
{x
x
x} expected value of x
x
x
J
k
(x
x
x
k
) value function
V
k
(x
x
x
k
,u
k
) input dependent value function
g
n
(x
x
x
n
,u
n
) cost function
k time index
n time index of prediction horizon
1 INTRODUCTION
Model Predictive Control (MPC), which is also re-
ferred to as Receding or Rolling Horizon Control, has
become more and more important for control applica-
tions from various fields. This is due to the fact that
not only the current system state, but also a model-
based prediction of future system states over a finite
N stage prediction horizon is considered in the control
law. For this prediction horizon, an open-loop optimal
control problem with a corresponding value function
is solved. Then the resulting optimal control input is
applied as a closed-loop control to the system.
The well understood and widely used MPC for
linear system models (Qin and Badgewell, 1997) to-
gether with linear or quadratic cost functions is not
always sufficient if it is necessary to achieve even
higher quality control, e.g. in high precision robot
control or in the process industry. Steadily grow-
ing requirements on the control quality can be met
by incorporating nonlinear system models and cost
functions in the control. The typically significant in-
crease in computational demand arising from the non-
linearities has been mitigated in the last years by the
steadily increasing available computation power for
control processes (Findeisen and Allg
¨
ower, 2002) and
advances in the employed algorithms to solve the con-
nected open-loop optimization (Ohtsuka, 2003).
62
Weissel F., F. Huber M. and D. Hanebeck U. (2007).
A CLOSED-FORM MODEL PREDICTIVE CONTROL FRAMEWORK FOR NONLINEAR NOISE-CORRUPTED SYSTEMS.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 62-69
DOI: 10.5220/0001625500620069
Copyright
c
SciTePress

Nevertheless, in most approaches, especially for
the important case of continuous state spaces, the in-
fluence of noise on the system is not considered (Ca-
macho and Bordons, 2004), which obviously leads to
unsatisfactory solutions especially for highly nonlin-
ear systems and cost functions. In (Deisenroth et al.,
2006) an extension of the deterministic cost func-
tion by a term considering the noise is presented. In
(Nikovski and Brand, 2003) an approach for infinite
horizon optimal control is presented, where a contin-
uous state space is discretized by means of a radial-
basis-function network. This approach leads to a con-
sideration of the noise influence, but as any discretiza-
tion suffers from the curse of dimensionality.
In technical applications, like robotics or sensor-
actuator-networks, discrete-time controllers for sys-
tems with continuous-valued state spaces, e.g. the
posture of a robot, but a finite set of control inputs,
e.g. turn left / right or move straight, are of special
importance. Therefore, in this paper a framework for
discrete-time NMPC for continuous state spaces and
a finite set of control inputs is presented that is based
on the efficient state prediction of nonlinear stochas-
tic models. Since an exact density representation in
closed form and with constant complexity is prefer-
able, a prediction method is applied that is founded
on the approximation of the involved system transi-
tion densities by axis-aligned Gaussian mixture den-
sities (Huber et al., 2006). To lower the computa-
tional demands for approximating multi-dimensional
transition densities, the so-called modularization for
complexity reduction purposes is proposed. Thus, the
Gaussian mixture representation of the predicted state
can be evaluated efficiently with high approximation
accuracy. As an additional part of this framework, an
extremely flexible representation of the cost function,
on which the optimization is based, is presented. Be-
sides the commonly used quadratic deviation, a versa-
tile Gaussian mixture representation of the cost func-
tion is introduced. This representation is very ex-
pressive due to the universal approximation property
of Gaussian mixtures. Combining the efficient state
prediction and the different cost function represen-
tations, an efficient integrated closed-form approach
to NMPC for nonlinear noise affected systems with
novel abilities is obtained.
The remainder of this paper is structured as fol-
lows: In the next section, the considered NMPC prob-
lem is described together with an example from the
field of mobile robot control. In Section 3, the ef-
ficient closed-form prediction approach for nonlin-
ear systems based on transition density approximation
and complexity reduction is derived. Different tech-
niques for modeling the cost function are introduced
in Section 4. In Section 5, three different kinds of
NMPC controllers are compared based on simulations
employing the example system, which has been intro-
duced in previous sections. Concluding remarks and
perspectives on future work are given in Section 6.
2 PROBLEM FORMULATION
The considered discrete-time system is given by
x
x
x
k+1
= a
(x
x
x
k
,u
k
,w
w
w
k
) , (1)
where x
x
x
k
denotes the vector-valued random variable
of the system state, u
k
the applied control input, and
a
(·) a nonlinear, time-invariant function. w
w
w
k
denotes
the white stationary noise affecting the system addi-
tively element-wise, i.e., the elements of w
w
w
k
are pro-
cessed in a
(·) just additively. For details see Sec-
tion 3.3.
Example System
A mobile two-wheeled differential-drive robot is supposed to
drive along a given trajectory, e.g. along a wall, with constant
velocity. This robot can be modeled by the distance to the
wall x
x
x
k
and its orientation relative to the wall α
α
α
k
, which leads
to the discrete-time nonlinear system description
x
x
x
k+1
= x
x
x
k
+ v· T · sin(α
α
α
k
) + w
w
w
x
k
,
α
α
α
k+1
= α
α
α
k
+ u
k
+ w
w
w
α
k
,
(2)
where x
x
x
k
= [x
x
x
k
,α
α
α
k
]
T
, v is a constant velocity, T the sampling
interval and w
w
w
x
k
and w
w
w
α
k
denote the noise influence on the
system. The input u
k
is a steering action, i.e., a change of
direction of the robot. Furthermore, the robot is equipped
with sensors to measure distance y
y
y
x
k
and orientation y
y
y
α
k
with
respect to the wall according to
y
y
y
x
k
= x
x
x
k
+ v
v
v
x
k
,
y
y
y
α
k
= α
α
α
k
+ v
v
v
α
k
,
(3)
where v
v
v
x
k
and v
v
v
α
k
describe the measurement noise.
At any time step k, the system state is predicted
over a finite N step prediction horizon. Then an open-
loop optimal control problem is solved, i.e., the opti-
mal input u
∗
k
is determined according to
u
∗
k
(x
x
x
k
) = argmin
u
k
V
k
(x
x
x
k
,u
k
)
with
V
k
(x
x
x
k
,u
k
) =
min
u
k+1
,...,
u
k+N−1
E
x
k+1
,...,
x
k+N
(
g
N
(x
x
x
k+N
) +
k+N−1
∑
n=k
g
n
(x
x
x
n
,u
n
)
)
, (4)
where the optimality is defined by a cumulative value
function J
k
(x
x
x
k
)
J
k
(x
x
x
k
) = min
u
k
V
k
(x
x
x
k
,u
k
) (5)
A CLOSED-FORM MODEL PREDICTIVE CONTROL FRAMEWORK FOR NONLINEAR NOISE-CORRUPTED
SYSTEMS
63

comprising the step costs g
n
(x
x
x
n
,u
n
) depending on the
predicted system states x
x
x
n
and the corresponding con-
trol inputs u
n
, as well as a terminal cost g
N
(x
x
x
k+N
).
This optimal control input u
∗
k
is then applied to the
system at time step k. In the next time step k + 1 the
whole procedure is repeated.
For most nonlinear systems, the analytical eval-
uation of (4) is not possible. One reason for this is
the required prediction of system states for a noise-
affected nonlinear system. The other one is the neces-
sity to calculate expected values, which also cannot be
performed in closed form. Therefore, in the next sec-
tions an integrated approach to overcome these two
problems is presented.
3 STATE PREDICTION
Predicting the system state is an important part in
NMPC for noise-affected systems. The probabil-
ity density
˜
f
x
k+1
(x
k+1
) of the system state x
x
x
k+1
for
the next time step k + 1 has to be computed uti-
lizing the so-called Chapman-Kolmogorov equation
(Schweppe, 1973)
˜
f
x
k+1
(x
k+1
) =
R
d
˜
f
T
u
k
(x
k+1
|x
k
)
˜
f
x
k
(x
k
)dx
k
. (6)
The transition density
˜
f
T
u
k
(x
k+1
|x
k
) depends on the
system described by (1). For linear systems with
Gaussian noise the Kalman filter (Kalman, 1960) pro-
vides an exact solution to (6), since this equation is
reduced to the evaluation of an integral over a multi-
plication of two Gaussian densities, which is analyti-
cally solvable.
For nonlinear systems, an approximate description
of the predicted density
˜
f
x
k+1
(x
k+1
) is inevitable, since
an exact closed-form representation is generally im-
possible to obtain. One very common approach in
context of NMPC is linearizing the system and then
applying the Kalman filter (Lee and Ricker, 1994).
The resulting single Gaussian density is typically not
sufficient for approximating
˜
f
x
k+1
(x
k+1
). Hence, we
propose representing all densities involved in (6) by
means of Gaussian mixtures, which can be done effi-
ciently due to their universal approximation property
(Maz’ya and Schmidt, 1996).
To reduce the complexity of approximating all
density functions corresponding to system (1) and
to allow for an efficient state prediction, the con-
cept of modularization is proposed, see Section 3.3.
Here, (1) is decomposed into vector-valued subsys-
tems. Approximations for these subsystems in turn
can be reduced to the scalar case, as stated in Sec-
tion 3.2. For that purpose, in the following section a
short review on the closed-form prediction approach
for scalar systems with additive noise is given. Em-
ploying this, modularization enables state prediction
for system (1) based on Gaussian mixture approxima-
tions of the transition density functions corresponding
to scalar systems.
3.1 Scalar Systems
For the scalar system equation
x
x
x
k+1
= a(x
x
x
k
,u
k
) + w
w
w
k
,
the approach proposed by (Huber et al., 2006) al-
lows to perform a closed-form prediction resulting
in an approximate Gaussian mixture representation
f
x
k+1
(x
k+1
) of
˜
f
x
k+1
(x
k+1
),
f
x
k+1
(x
k+1
) =
L
∑
i=1
ω
i
·
N (x
k+1
− µ
i
;σ
2
i
) , (7)
where L is the number of Gaussian components,
N (x
k+1
− µ
i
;σ
2
i
) is a Gaussian density with mean
µ
i
, standard deviation σ
i
, and weighting coefficients
ω
i
with ω
i
> 0 as well as
∑
L
i=1
ω
i
= 1. For obtain-
ing this approximate representation of the true pre-
dicted density that provides high accuracy especially
with respect to higher-order moments and a mul-
timodal shape, the corresponding transition density
˜
f
T
u
k
(x
k+1
|x
k
) from (6) is approximated off-line by the
Gaussian mixture
f
T
u
k
(x
k+1
,x
k
,η
)
=
L
∑
i=1
ω
i
·
N (x
k+1
− µ
i,1
;σ
2
i,1
)·
N (x
k
− µ
i,2
;σ
2
i,2
)
with parameter vector
η
= [η
T
1
,. . . ,η
T
L
]
T
,
comprising L axis-aligned Gaussian components
(short: axis-aligned Gaussian mixture), i.e., the co-
variance matrices of the Gaussian components are di-
agonal, with parameters
η
T
i
= [ω
i
,µ
i,1
,σ
i,1
,µ
i,2
,σ
i,2
] .
The axis-aligned structure of the approximate tran-
sition density allows performing repeated prediction
steps with constant complexity, i.e., a constant num-
ber L of mixture components for f
x
k+1
(x
k+1
).
This efficient prediction approach can be directly
applied to vector-valued systems, like (1). However,
off-line approximation of the multi-dimensional tran-
sition density corresponding to such a system is com-
putationally demanding. Therefore, in the next two
sections techniques to lower the computational bur-
den are introduced.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
64

Unit Delay
x
k
a
(1)
(x
k
, u
k
)
x
(2)
k
+
w
(1)
k
+
· · ·
w
(2)
k
+
w
(m)
k
x
(m)
k
x
k+1
a
(2)
(x
(2)
k
, u
k
) a
(m)
(x
(m)
k
, u
k
)
u
k
Figure 1: Modularization of the vector valued system x
x
x
k+1.
= a
(x
x
x
k
,u
k
,w
w
w
k
).
3.2 Vector-Valued Systems
Now we consider the vector-valued system
x
x
x
k+1
= a
(x
x
x
k
,u
k
) + w
w
w
k
, (8)
with x
x
x
k+1
= [x
x
x
k+1,1
,x
x
x
k+1,2
,. . . ,x
x
x
k+1,d
]
T
∈ R
d
and
noise w
w
w
k
= [w
w
w
k,1
,w
w
w
k,2
,. . . ,w
w
w
k,d
]
T
∈ R
d
. Assuming w
w
w
k
to be white and stationary (but not necessarily Gaus-
sian or zero-mean), with mutually stochastically in-
dependent elements w
w
w
k, j
, approximating the corre-
sponding transition density
˜
f
T
u
k
(x
k+1
|x
k
) =
˜
f
w
(x
k+1
−
a
(x
k
,u
k
)) can be reduced to the scalar system case.
Theorem 1 (Composed Transition Density)
The transition density
˜
f
T
u
k
(x
k+1
|x
k
) of system (8)
is composed of separate transition densities of the
scalar systems a
j
(· ), j = 1,2,. . . ,d, where a
(· ) =
[a
1
(· ), a
2
(· ), . ..,a
d
(· )]
T
.
PROOF. Marginalizing
˜
f
x
k+1
(x
k+1
) from the joint density
function
˜
f
k
(x
k+1
,x
k
,w
k
) and separating the elements of w
w
w
k
leads to
˜
f
x
k+1
(x
k+1
)
=
R
2d
δ(x
k+1
−a
(x
k
,u
k
)−w
k
)
˜
f
x
k
(x
k
)
˜
f
w
(w
k
)dx
k
dw
k
=
R
2d
d
∏
j=1
δ(x
k+1, j
− a
j
(x
k
,u
k
) − w
k, j
)
·
˜
f
x
k
(x
k
)
d
∏
j=1
˜
f
w
j
(w
k, j
)dx
k
dw
k
=
R
d
d
∏
j=1
˜
f
w
j
x
k+1, j
− a
j
(x
k
,u
k
)
|
{z }
separate transition densities
!
˜
f
x
k
(x
k
)dx
k
.
As a result of the mutually stochastically independence of
the elements in w
w
w
k
, the transition density of the vector-
valued system (8) is separated into d transition densities of
d scalar systems. Approximating these lower-dimensional
transition densities is possible with decreased computa-
tional demand (Huber et al., 2006).
The concept of modularization, introduced in the
following section, benefits strongly from the result
obtained in Theorem 1.
3.3 Concept of Modularization
For our proposed NMPC framework, we assume that
the nonlinear system is corrupted by element-wise ad-
ditive noise. Incorporating this specific noise struc-
ture, the previously stated closed-form prediction step
can indirectly be utilized for system (1). Similar to
Rao-Blackwellised particle filters (de Freitas, 2002),
we can reduce the system in (1) to a set of less com-
plex subsystems with a form according to (8),
x
x
x
k+1
= a
(x
x
x
k
,u
k
,w
w
w
k
) = a
(m)
(x
x
x
(m)
k
,u
k
) + w
w
w
(m)
k
x
x
x
(m)
k
= a
(m−1)
(x
x
x
(m−1)
k
,u
k
) + w
w
w
(m−1)
k
.
.
.
x
x
x
(2)
k
= a
(1)
(x
x
x
(1)
k
,u
k
) + w
w
w
(1)
k
.
We name this approach modularization, where the
subsystems
x
x
x
(i+1)
k
= a
(i)
(x
x
x
(i)
k
,u
k
) + w
w
w
(i)
k
, for i = 1, ...,m
correspond to transition densities, that can be approx-
imated according to Section 3.1 and 3.2. Since these
subsystems are less complex than the overall sys-
tem (1), approximating transition densities is also less
complex. Furthermore, a nested prediction can be
performed to obtain the predicted density f
x
k+1
(x
k+1
),
see Fig. 1. Starting with x
x
x
(1)
k
= x
x
x
k
, each subsystem
a
(i)
(· ) receives an auxiliary system state x
x
x
(i)
k
and gen-
erates an auxiliary predicted system state x
x
x
(i+1)
k
.
The noise w
w
w
k
is separated into its subvectors w
w
w
(i)
k
according to
w
w
w
k
= [w
w
w
(1)
k
,w
w
w
(2)
k
,. . . ,w
w
w
(m)
k
]
T
,
in case that the single noise subvectors w
w
w
(i)
k
are mutu-
ally independent.
Example System: Modularization
The system model (2) describing the mobile robot can be
modularized into the subsystems
x
x
x
(2)
k
= sin(α
α
α
k
) + w
w
w
x
k
A CLOSED-FORM MODEL PREDICTIVE CONTROL FRAMEWORK FOR NONLINEAR NOISE-CORRUPTED
SYSTEMS
65
and
x
x
x
k+1
= x
x
x
k
+ v· T · x
x
x
(2)
k
,
α
α
α
k+1
= α
α
α
k
+ u
k
+ w
w
w
α
k
.
The auxiliary system state x
x
x
(2)
k
is stochastically dependent
on α
α
α
k
. We omitted this dependence in further investigations
of the example system for simplicity.
Please note that there are typically stochastic de-
pendencies between several auxiliary system states.
To consider this fact, the relevant auxiliary system
states have to be augmented to conserve the depen-
dencies. Thus, the dimensions of these auxiliary
states need not all to be equal.
4 COST FUNCTIONS
In this section, two possibilities to model cost func-
tions, the well known quadratic deviation and a novel
approach employing Gaussian mixture cost functions,
are presented. Exploiting the fact that the predicted
state variables are, as explained in the previous sec-
tion, described by Gaussian mixture densities, the
necessary evaluation of the expected values in (4) can
be calculated efficiently in closed-form for both op-
tions.
In the following, cumulative value functions ac-
cording to (5) are considered, where g
n
(x
x
x
n
,u
n
) de-
notes a step cost within the horizon and g
N
(x
x
x
n
) a cost
depending on the terminal state at the end of the hori-
zon. The value function J
k
(x
x
x
k
) is the minimal cost for
the next N steps of the system, starting at state x
x
x
k
plus
the terminal cost g
N
(x
x
x
n
).
For simplicity, step costs that are additively de-
composable according to
g
n
(x
x
x
n
,u
n
) = g
x
n
(x
x
x
n
) + g
u
n
(u
n
)
are considered, although the proposed framework is
not limited to this case.
4.1 Quadratic Cost
One of the most popular cost functions is the
quadratic deviation from a target value ˇx
or ˇu accord-
ing to
g
x
n
(x
x
x
n
) = (x
x
x
n
− ˇx
n
)
T
(x
x
x
n
− ˇx
n
) .
As in our framework the probability density func-
tion of the state x
x
x
n
is given by an axis-aligned Gaus-
sian mixture f
x
n
(x
n
) with L components, the calcula-
tion of E
x
x
x
n
{g
x
n
(x
x
x
n
)}, which is necessary to compute
−2 0 2 4 6 8 10
−1
−0.8
−0.6
−0.4
−0.2
0
x
n
→
g
x
n
→
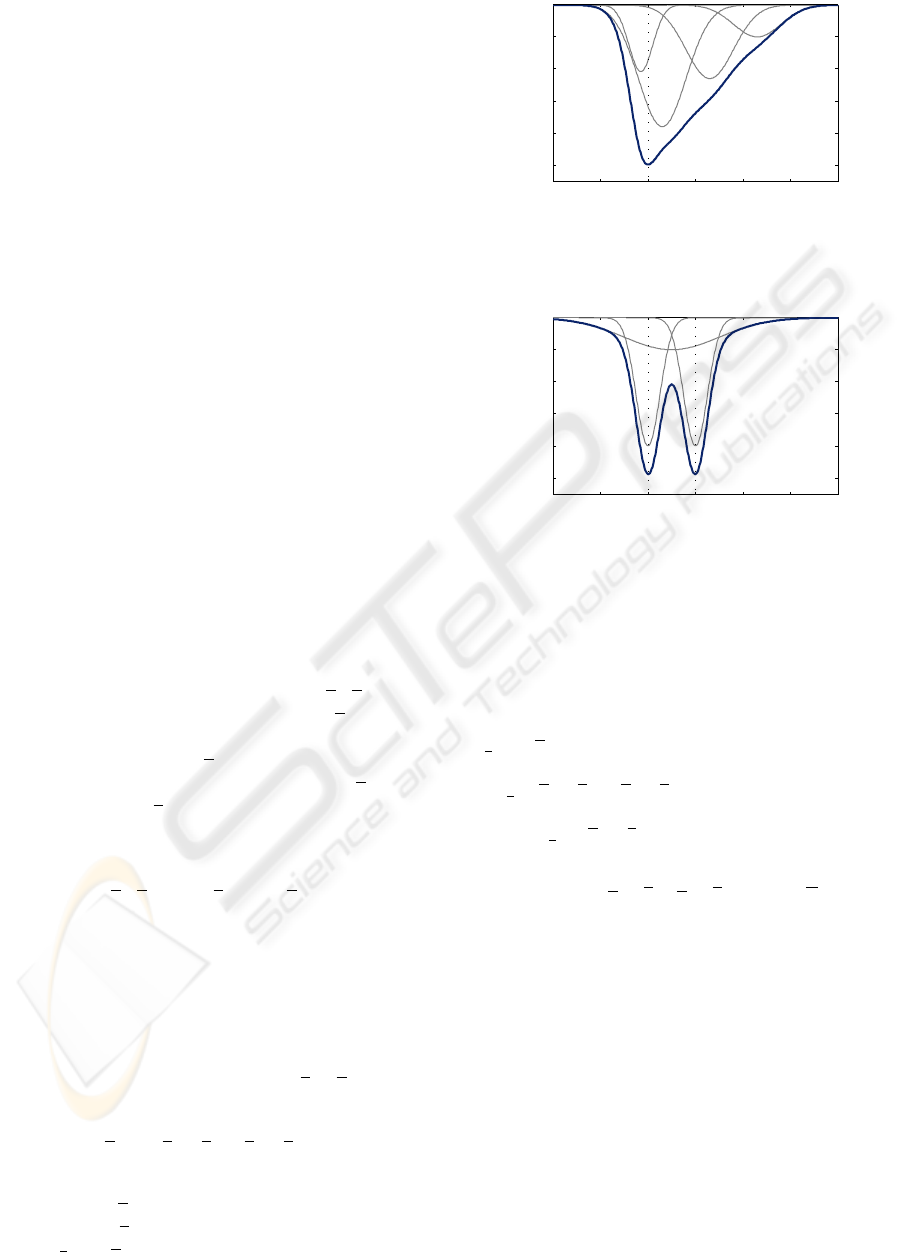
Figure 2: Asymmetric cost function consisting of four com-
ponents (gray) with a minimum at ˇx
n
= 2.
−2 0 2 4 6 8 10
−1
−0.8
−0.6
−0.4
−0.2
0
x
n
→
g
x
n
→
Figure 3: Multimodal cost function consisting of three com-
ponents (gray) with minima at ˇx
a
n
= 2, ˇx
b
n
= 4.
(4), can be performed analytically as it can be inter-
preted as the sum over shifted and dimension-wise
calculated second-order moments
E
x
x
x
n
{g
x
n
(x
x
x
n
)}
= E
x
x
x
n
{(x
x
x
n
− ˇx
n
)
T
(x
x
x
n
− ˇx
n
)}
= trace E
2
x
x
x
n
{(x
x
x
n
− ˇx
n
)}
= trace
L
∑
i=1
ω
i
(µ
i
− ˇx
n
)(µ
i
− ˇx
n
)
T
+ diag(σ
i
)
2
,
employing E
2
x
x
x
{x
x
x} =
∑
L
i=1
ω
i
(µ
2
i
+ σ
2
i
).
Example System: Quadratic Cost
If the robot is intended to move parallel along the wall, the
negative quadratic deviation of the angle α
α
α
k
with respect to
the wall, i.e., g
α
n
(α
α
α
n
) = (α
α
α
n
−α
Wall
n
)
2
is a suitable cost func-
tion.
4.2 Gaussian Mixture Cost
A very versatile description of the cost function can
be realized if Gaussian mixtures are employed. In this
case, arbitrary cost functions can be realized due to
the Gaussian mixtures’ universal approximation prop-
erty (Maz’ya and Schmidt, 1996). Obviously, in this
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
66

case the Gaussian mixtures may have arbitrary param-
eters, e.g. negative weights ω.
Example System: Gaussian Mixture Cost Function
In case the robot is intended to move at a certain optimal
distance to the wall (e.g. ˇx
n
= 2, with x
Wall
n
= 0), where
being closer to the wall is considered less desirable than
being farther away, this can, e.g. be modeled with a cost
function as depicted in Fig. 2. If two different distances are
considered equally optimal, this can be modeled with a cost
function as depicted in Fig. 3.
Please note that assigning rewards to a state is
equivalent to assigning negative costs, which leads
to the depicted negative cost functions in Fig. 2 and
Fig. 3.
Here, the calculation of the expected value
E
x
x
x
n
{g
x
n
(x
x
x
n
)}, which is necessary for the calculation
of (4), can also be performed analytically
E
x
x
x
n
{g
x
n
(x
x
x
n
)}
=
R
d
f
x
n
(x
n
)· g
x
n
(x
n
)dx
n
=
R
d
L
∑
i=1
ω
i
N (x
n
− µ
i
;diag(σ
i
)
2
)
·
M
∑
j=1
ω
j
N (x
n
− µ
j
;diag(σ
j
)
2
)dx
n
=
L
∑
i=1
M
∑
j=1
ω
ij
R
d
N (x
n
− µ
ij
;diag(σ
ij
)
2
)dx
n
|
{z }
=1
,
with
ω
ij
= ω
i
ω
j
·
N (µ
i
− µ
j
;diag(σ
i
)
2
+ diag(σ
j
)
2
) ,
where f
x
n
(x
n
) denotes the L-component Gaussian
mixture probability density function of the system
state (7) and g
x
n
(x
x
x
n
) the cost function, which is a Gaus-
sian mixture with M components.
4.3 Input Dependent Part
The input dependent part of the cost function g
u
n
(u
n
)
can either be modeled similar to the procedures de-
scribed above or with a lookup-table since there is just
a finite number of discrete u
n
.
Using the efficient state prediction presented in
Section 3 together with the value function representa-
tions presented above, (4) can be solved analytically
for a finite set of control inputs. Thus, an efficient
closed-form solution for the optimal control problem
within NMPC is available. Its capabilities will be il-
lustrated by simulations in the next section.
5 SIMULATIONS
Based on the above example scenario, several simula-
tions are conducted to illustrate the modeling capabil-
ities of the proposed framework as well as to illustrate
the benefits that can be gained by the direct consid-
eration of noise in the optimal control optimization.
The considered system is given by (2) and (3), with
v· T = 1 and u
k
∈ {−0.2,−0.1, 0, 0.1, 0.2}. The con-
sidered noise influences on the system w
w
w
x
k
and w
w
w
α
k
are
zero-mean white Gaussian noise with standard devia-
tion σ
x
w
= 0.5 and σ
α
w
= 0.05 ≈ 2.9
◦
respectively. The
measurement noise is also zero-mean white Gaus-
sian noise with standard deviation σ
x
v
= 0.5 and σ
α
v
=
0.1 ≈ 5.7
◦
. All simulations are performed for a N = 4
step prediction horizon, with a value function accord-
ing to (5), where g
N
(x
x
x
k+N
) is the function depicted in
Fig. 2 and g
n
(x
x
x
n
,u
n
) = g
N
(x
x
x
k+N
) ∀n. In addition, the
modularization is employed as described above.
To evaluate the benefits of the proposed NMPC
framework, three different kind of simulations are
performed:
Calculation of the input without noise considera-
tion (deterministic NMPC):
The deterministic control is calculated as a bench-
mark neglecting the noise influence.
Direct calculation of the optimal input considering
all noise influences (stochastic NMPC):
The direct calculation of the optimal input with con-
sideration of the noise is performed using the tech-
niques presented in the previous sections. Thus, it is
possible to execute all calculations analytically with-
out the need for any numerical methods. Still, this
approach has the drawback that the computational de-
mand for the optimal control problem increases expo-
nentially with the length of the horizon N. Thus, this
approach is suitable for short horizons only.
Calculation of the optimal input with a value
function approximation scheme and Dynamic Pro-
gramming (stochastic NMPC with Dynamic Pro-
gramming):
In order to be able to use the framework efficiently
also for long prediction horizons, it is necessary to
employ Dynamic Programming (DP). Unfortunately,
this is not directly possible, as no closed-form so-
lution for the value function J
n
is available. One
easy but either not very accurate or computation-
ally demanding solution would be to discretize the
state space. More advanced solutions can be found
by value function approximation (Bertsekas, 2000).
For the simulations, an especially well-suited case of
A CLOSED-FORM MODEL PREDICTIVE CONTROL FRAMEWORK FOR NONLINEAR NOISE-CORRUPTED
SYSTEMS
67

0 5 10 15 20 25 30 35 40
0
2
4
6
k →
x
k
→
(b) Cost per step.
(a) Position and orientation.
0 5 10 15 20 25 30 35 40
−1
−0.5
0
k →
g
k
→
g
det
k
g
DP
k
g
k
Figure 4: First 40 steps of a simulation (red solid line: stochastic NMPC, green dotted line: stochastic NMPC with DP, blue
dashed line: deterministic NMPC).
value function approximation is employed that has
been described by (Nikovski and Brand, 2003). Here,
the state space is discretized by covering it with a
finite set of Gaussians with fixed means and covari-
ances. Then weights, i.e., scaling factors, are selected
in such a way that the approximate and the true value
function coincide at the means of every Gaussian. Us-
ing these approximate value functions together with
the techniques described above, again all calculations
can be executed analytically. In contrast to the di-
rect calculation, now the computational demand in-
creases only linearly with the length of the predic-
tion horizon but quadratically in the number of Gaus-
sians used to approximate the value function. Here,
the value functions are approximated by a total of 833
Gaussians equally spaced over the state space within
( ˆx
n
,
ˆ
α
n
) ∈ Ω := [−2, 10] × [−2,2].
For each simulation run, a particular noise realiza-
tion is used that is applied to the different controllers.
In Fig. 4(a), the first 40 steps of a simulation run are
shown. The distance to the wall x
k
is depicted by the
position of the circles, the orientation α
k
by the orien-
tation of the arrows. Besides that the system is heav-
ily influenced by noise, it can be clearly seen that the
robot under deterministic control behaves very differ-
ently from the other two. The deterministic controller
just tries to move the robot to the minimum of the
cost function at ˇx
k
= 2 and totally neglects the asym-
metry of the cost function. The stochastic controllers
lead to a larger distance to the wall, as they consider
the noise affecting the system in conjunction with the
non-symmetric cost function.
In Fig. 4(b), the evaluation of the cost function for
each step is shown. As expected, both stochastic con-
trollers perform much better, i.e., they generate less
Table 1: Simulation Results.
controller average cost
deterministic -0.6595 (100.00%)
stochastic -0.7299 (110.66%)
stochastic DP -0.6824 (103.48%)
cost, than the deterministic one. This finding has been
validated by a series of 100 Monte Carlo simulations
with different noise realizations and initial values.
The uniformly distributed initial values are sampled
from the interval x
0
∈ [0,8] and α
0
∈ [−π/4,π/4].
In Table 1, the average step costs of the 100 simu-
lations with 40 steps each are shown. To facilitate the
comparison, also normalized average step costs are
given. Here, it can be seen that the stochastic con-
troller outperforms the deterministic one by over 10%
in terms of cost. In 82% of the runs, the stochastic
controller gives overall better results than the deter-
ministic one. By employing dynamic programming
together with value function approximation the bene-
fits are reduced. Here, the deterministic controller is
only outperformed by approximately 3.5%. The anal-
ysis of the individual simulations leads to the conclu-
sion that the control quality significantly degrades in
case the robot attains a state which is less well ap-
proximated by the value function approximation as it
lies outside Ω. Still, the dynamic programming ap-
proach produced better results than the deterministic
approach in 69% of the runs. These findings illustrate
the need for advanced value function approximation
techniques in order to gain the very good control per-
formance of the direct stochastic controller together
with the efficient calculation of the DP approach.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
68

6 CONCLUSIONS
A novel framework for closed-form Nonlinear Model
Predictive Control (NMPC) for continuous state space
and a finite set of control inputs has been presented
that directly incorporates the noise influence in the
corresponding optimal control problem. By using the
proposed state prediction methods, which are based
on transition density approximation by Gaussian mix-
ture densities and complexity reduction techniques,
the otherwise not analytically solvable state predic-
tion of nonlinear noise affected systems can be per-
formed in an efficient closed-form manner. Another
very important aspect of NMPC is the modeling of the
cost function. The proposed methods also use Gaus-
sian mixtures, which leads to a level of flexibility far
beyond the traditional representations. By employing
the same representation for both the predicted proba-
bility density functions and the cost functions, NMPC
is solvable in closed-form for nonlinear systems with
consideration of noise influences. The effectiveness
of the presented framework and the importance of
the consideration of noise in the controller have been
shown in simulations of a two-wheeled differential-
drive robot following a specified trajectory.
Future research is intended to address various top-
ics. One is the optimization of the value function ap-
proximation by abandoning a fixed grid in order to in-
crease performance and accuracy. An additional im-
portant task will be the consideration of stability as-
pects, especially in cases of approximated value func-
tions. This can, e.g. be tackled by the use of bounding
techniques for the approximation error (Lincoln and
Rantzer, 2006). Another interesting extension will be
the incorporation of effects of inhomogeneous noise,
i.e., noise with state and/or input dependent noise lev-
els. Together with the incorporation of nonlinear fil-
tering techniques this is expected to increase the con-
trol quality even more.
Besides the addition of new features to the frame-
work, also the extension to new application fields is
intended. Of special interest is the extension of Model
Predicted Control to the related emerging field of
Model Predictive Sensor Scheduling (He and Chong,
2004), which is of special importance, e.g. in sensor-
actuator-networks.
REFERENCES
Bertsekas, D. P. (2000). Dynamic Programming and Op-
timal Control. Athena Scientific, Belmont, Mas-
sachusetts, U.S.A., 2nd edition.
Camacho, E. F. and Bordons, C. (2004). Model Predictive
Control. Springer-Verlag London Ltd., 2 edition.
Deisenroth, M. P., Ohtsuka, T., Weissel, F., Brunn, D., and
Hanebeck., U. D. (2006). Finite-Horizon Optimal
State Feedback Control of Nonlinear Stochastic Sys-
tems Based on a Minimum Principle. In Proc. of the
IEEE Int. Conf. on Multisensor Fusion and Integra-
tion for Intelligent Systems, pages 371–376.
Findeisen, R. and Allg
¨
ower, F. (2002). An Introduction to
Nonlinear Model Predictive Control. In Scherer, C.
and Schumacher, J., editors, Summerschool on ”The
Impact of Optimization in Control”, Dutch Institute of
Systems and Control (DISC), pages 3.1–3.45.
de Freitas, N. (2002). Rao-Blackwellised Particle Filtering
for Fault Diagnosis. In IEEE Aerospace Conference
Proceedings, volume 4, pages 1767–1772.
He, Y. and Chong, E. K. P. (2004). Sensor Scheduling for
Target Tracking in Sensor Networks. In Proceedings
of the 43rd IEEE Conference on Decision and Control,
volume 1, pages 743–748.
Huber, M., Brunn, D., and Hanebeck, U. D. (2006). Closed-
Form Prediction of Nonlinear Dynamic Systems by
Means of Gaussian Mixture Approximation of the
Transition Density. In Proc. of the IEEE Int. Conf.
on Multisensor Fusion and Integration for Intelligent
Systems, pages 98–103.
Kalman, R. E. (1960). A new Approach to Linear Filtering
and Prediction Problems. Transactions of the ASME,
Journal of Basic Engineering, (82):35–45.
Lee, J. H. and Ricker, N. L. (1994). Extended Kalman Filter
Based Nonlinear Model Predictive Control. In Indus-
trial & Engineering Chemistry Research, pages 1530–
1541. ACS.
Lincoln, B. and Rantzer, A. (2006). Relaxing Dynamic Pro-
gramming. IEEE Transactions on Automatic Control,
51(8):1249–1260.
Maz’ya, V. and Schmidt, G. (1996). On Approximate Ap-
proximations using Gaussian Kernels. IMA Journal of
Numerical Analysis, 16(1):13–29.
Nikovski, D. and Brand, M. (2003). Non-Linear Stochas-
tic Control in Continuous State Spaces by Exact In-
tegration in Bellman’s Equations. In Proc. of the
2003 International Conf. on Automated Planning and
Scheduling, pages 91–95.
Ohtsuka, T. (2003). A Continuation/GMRES Method for
Fast Computation of Nonlinear Receding Horizon
Control. Automatica, 40(4):563–574.
Qin, S. J. and Badgewell, T. A. (1997). An Overview of In-
dustrial Model Predictive Control Technology. Chem-
ical Process Control, 93:232–256.
Schweppe, F. C. (1973). Uncertain Dynamic Systems.
Prentice-Hall.
A CLOSED-FORM MODEL PREDICTIVE CONTROL FRAMEWORK FOR NONLINEAR NOISE-CORRUPTED
SYSTEMS
69
