ENHANCING KAPPA NUMBER CONTROL IN DOWNFLOW

LO-SOLIDS

T M

DIGESTER USING DIAGNOSIS AND MODELLING

Timo Ahvenlampi

University of Oulu, Systems Engineering Laboratory, 90014 University of Oulu, Finland

Rami Rantanen

Metso Automation Inc., Process Automation Systems, Tampere, Finland

Keywords:

Fault tolerant, pulp industry, monitoring, controllability.

Abstract:

In this study, Kappa number prediction and diagnosis in continuous Downﬂow Lo-Solids

T M

cooking appli-

cation is investigated. Gustafson’s Kappa number model is applied for the prediction of the blowline Kappa

number. New cooking temperature set point is solved iteratively based on the difference between the pre-

dicted and target blow-line kappa numbers. The main active variables for the Kappa number are monitored

using self-organizing map (SOM). The diagnosis and Kappa control are combined into a fault tolerant system.

The data is collected from industrial continuous Downﬂow Lo-Solids

T M

cooking digester. Good results were

achieved using the proposed approach.

1 INTRODUCTION

The question how the overall system of the sub

processes and chains of sub processes can be im-

proved, by means of fault diagnosis (see e.g. (Iser-

mann, 1997), (Venkatasubramanian et al., 2003a) and

(Venkatasubramanian et al., 2003b)), has not fully an-

swered. In particular, this holds for demanding pro-

cess conditions such as found in chemical and me-

chanical pulping. Modern processes generate a lot

of information, which can be used for improving

the operation of the process and quality of the prod-

ucts. This can be accomplished by combining expert

knowledge, modelling, control and fault diagnosis.

The pulp digester is very important unit opera-

tion in the chemical pulping plant. The control ac-

tions in the digester have effects to the entire ﬁber

line operations. Also the quality of the pulp in the

digester should be achieved with minimal cooking

costs. (Leivisk

a, 2000) The quality of the chemical

pulping is characterized e.g. by the pulp’s strength,

viscosity, yield and Kappa number. Usually only

Kappa number is measured on-line. The on-line mea-

surement is located in the blow line of the digester.

Thus, the main control actions are observed only af-

ter the delay time of the cooking and washing zones.

The delay time can be several hours. By the predic-

tion of the Kappa number prior to the cooking zone

more information is provided to be applied in accu-

rate control actions. The prediction indicates changes

in the blow line Kappa number. The main control of

the pulp quality should be applied in the pulp digester.

The control of the pulp quality is more challenging

in the following subprocesses of the plant, if the pulp

quality (Kappa number) is out of the good quality area

after the digester.

The fault diagnosis is needed to ensure accurate

quality control of the chemical processes. Diagno-

sis of the chemical processes are studied in many pa-

pers, see e.g. ((Dash et al., 2003) and (Qian et al.,

2003)). In the ﬁeld of chemical pulping, there are

not too many publications concerning fault diagno-

sis. Puranen (Puranen, 1999) has formed a distur-

bance index for process operators to be able to ob-

serve faulty process situations. In that study measure-

ments, means and deviations are combined by fuzzy

logic. Diagnosis of the digester has been also studied

in papers (Ahvenlampi et al., 2005) and (Tervaskanto

et al., 2005).

In large industrial plants, every sub process has its

own task and the entire plant is working properly if

all the sub processes are functioning effectively. A

faulty operation in one sub process usually changes

the performance of the entire plant. Therefore, faults

161

Ahvenlampi T. and Rantanen R. (2007).

ENHANCING KAPPA NUMBER CONTROL IN DOWNFLOW LO-SOLIDSTM DIGESTER USING DIAGNOSIS AND MODELLING.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 161-166

DOI: 10.5220/0001626201610166

 SciTePress

have to be found as quickly as possible and decisions

that stop the propagation of their effects have to be

made (Blanke et al., 2003). Active Fault Tolerant

Control (AFTC) detects and isolates possible faults

in the system and also reconﬁgures the control law

(Mahmoud et al., 2003). In paper (Simani and Patton,

2002), a robust model-based technique for the diag-

nosis of faults in a chemical process has been devel-

oped. The system consists of a fuzzy combination of

Takagi-Sugeno models. Fault Detection and Identiﬁ-

cation (FDI) is then applied by using residual analysis

and geometrical tests.

In this study a continuous kraft cooking applica-

tion is investigated. Most of the kraft pulp is produced

in the continuous digesters (Gullichsen, 2000). In a

typical chemical pulping process, the pre-treated and

penetrated wood chips are fed into the impregnation

vessel and pulp digester where lignin is removed from

the chips with the aid of chemical reactions. The main

active variables for the Kappa number are tempera-

ture, alkali concentration, cooking (residence) time

and the wood species. The main lignin removal takes

place in the cooking zone in the digester, where the

temperature is signiﬁcantly higher than in the impreg-

nation vessel.

Applied Kappa number model (Gustafson’s

Kappa number model (Gustafson et al., 1983)) is also

used in the real-time Kappa number modeling. The

results for the conventional cooking process are pre-

sented in paper (Rantanen et al., 2003) and in the

Downﬂow Lo-Solids

T M

cooking process in paper

(Rantanen et al., 2005).

In earlier study by the authors (Ahvenlampi et al.,

2006), the proposed system was applied for the con-

ventinal kraft cooking process. In this paper, the same

approach is tested with Downﬂow Lo-Solids

T M

kraft

cooking process.

The aim of this approach has been to improve

the Kappa number control by combining diagnosis

(Ahvenlampi and Kortela, 2005) and new control

strategy for Kappa number control (Rantanen, 2006).

The used monitoring method is self-organizing map

(SOM) (Kohonen, 1997). The evaluation of the prob-

lems in the process is performed by quantization error.

If the quantization error is notable, the Kappa number

prediction has been stopped.

The blow line Kappa number is predicted before

cooking zone. Thus, the cooking temperature can be

controlled. In the Kappa number control strategy, the

cooking temperature’s set point is determined by us-

ing only the Kappa number model.

The structure of the paper is an following. The

methods used are presented in chapter 2. The pro-

posed fault tolerant control system is presented in the

chapter 3. Case study is considered in chapter 4 and

discussion and conclusions are shown in chapters 5

and 6.

2 METHODS USED

In this chapter, methods used are presented. Em-

pirical and experimental methods were applied.

Gustafson’s Kappa number model is an empirical

model for deligniﬁcation. The monitoring method,

SOM, (Kohonen, 1997) is also presented.

2.1 Gustafson’s Kappa Number Model

Gustafson et al. (Gustafson et al., 1983) have derived

a mathematical model consisting of a series of dif-

ferential equations describing the combined diffusion

and kinetics within a wood chip during the kraft pulp-

ing process.

The lignin removal in the impregnation vessel can

be calculated using Gustafson’s Kappa number model

for the initial phase. The rate equation for the initial

phase deligniﬁcation is:

= k

(17.5−8760/T )

L (1)

where L is the lignin content at time t,

is a species speciﬁc constant and

T is temperature in Kelvin.

The rate equation for the bulk phase (cooking

zone) deligniﬁcation is:

∂L

∂t

= k

0bl

−B

/T )



−



L + (2)

1bl

−B

/T )



−



0.5



−



0.4

where [OH

−

] is the hydroxyl ion concentration,

[HS

−

] is the hydrosulphide ion concentration and

0bl

, k

1bl

, A

, B

and B

are species speciﬁc

constants.

The relative reaction rate is higher in the bulk

phase than in the other phases.

Residual deligniﬁcation happens in the washing

zone and it is formulated as:

∂L

∂t

= k

(19.64−10804/T )



−



0.7

L, (3)

where k

is a species speciﬁc constant for residual

deligniﬁcation.

The relative rate decreases, and the effect of hy-

droxyl ion concentration decreases in the residual

phase. Parameters k

, A

and B

are presented in

(Rantanen, 2006).

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

162

K a p p a n u m b e r

p r e d i c t i o n (

= 1 ) o r

i t e r a t i o n m o d e l (

> 1 )

p r e d i c t e d

b l o w - l i n e

K a p p a #

b l o w - l i n e

K a p p a #

t a r g e t

R e a l - t i m e

K a p p a n u m b e r

m o d e l

n o

y e s

d i f f =

p r e d i c t e d K # -

K # t a r g e t

d T =

f (

d i f f

)

T + d T

E A + d E A

i s

a b s ( d i f f )

< s i g m a

T _ s e t p o i n t = T _ s e t p o i n t

k - 1

E A _ s e t p o i n t = E A _ s e t p o i n t

k - 1

p r o c e s s d a t a a t

p r e d i c t i o n p o i n t

E A

i s

= 1 ?

d E A =

f (

d i f f

)

y e s

n o

d T =

f (

d i f f

)

i s

= 1 ?

y e s

T _ s e t p o i n t = T + d T

E A _ s e t p o i n t = E A + d E A

n o

p r o f i l e s b e f o r e

p r e d i c t i o n p o i n t

= 1

+ 1

Figure 1: Structure of the new Kappa number control strat-

egy.

2.2 Self-organizing Map

The SOM (Kohonen, 1997) is an unsupervised artiﬁ-

cial neural network. The network is normally a two-

dimensional mapping / projection of the data group.

The visualization of the map is easier with a two-

dimensional map. In the training of the SOM net-

work, data points are sequentially introduced to the

SOM. In each iteration, the SOM neuron which is

closest to the input unit is selected by the equation

(4). This unit is the Best Matching Unit (BMU) or

winner.

kz − c

k = min

{kz − c

k} (4)

where z is input vector,

is the selected center, Best Matching Unit

(BMU), and

is the current center in the evaluation.

The weight vectors are updated using the follow-

ing formula. Only the weight vectors which are inside

the neighborhood radius h

, are updated.

(t + 1) = c

(t) + h

(t) [z (t) − c

(t)] (5)

U p p e r e x t r a c t i o n

C o o k i n g

c i r c u l a t i o n

L o w e r e x t r a c t i o n

B l o w - l i n e

C h i p s

L i q u o r

W a s h i n g l i q u o r

F e e d

c i r c u l a t i o n

F e e d c i r c u l a t i o n

T 1

T 2

T 3 ,

A 2

T 4

T 5 , A 3

T 6 , A 4

T 7 , A 5

T 8

C h i p s

S t e a m

E x h a u s t

( a )

( c )

( d )

( e )

( b )

( a ) = c h i p b i n

( b ) = c h i p m e t e r

( c ) = l o w p r e s s u r e f e e d e r

( d ) = s t e a m i n g v e s s e l

( e ) = h i g h p r e s s u r e f e e d e r

( f ) = i m p r e g n a t i o n v e s s e l

( g ) = d i g e s t e r

( f )

( g )

W h i t e

l i q u o r , A 1

W h i t e

l i q u o r , A 1

Figure 2: Impregnation vessel and continuous cooking di-

gester.

3 KAPPA NUMBER CONTROL

In industrial plants, the Kappa number control is usu-

ally performed by the H-factor (Vroom, 1957). The

H-factor expresses the cooking temperature and time

as a single variable. Based on the difference between

the predicted Kappa number and the Kappa number

target the H-factor and temperature proﬁle are cor-

rected. One weakness of the H-factor is that depend-

ing on the variations in chip quality etc. different H-

factors are needed, although the process conditions

were otherwise the same. To overcame this prob-

lem new methods have been introduced. In this pa-

per, Kappa number control strategy with and without

a fault tolerant part is presented.

3.1 Kappa Number Control Strategy

New Kappa number control strategy is presented in

study (Rantanen, 2006). In the approach, only Kappa

number model is applied. That is the main difference

compared to the use of Vroom’s H-factor and Hatton’s

Kappa number model (Hatton, 1973). Thus, no sepa-

rate models are needed to cover the effects of temper-

ature, chemical concentrations and cooking time. The

control of the alkali proﬁle could also be improved by

using the Kappa number model. In this paper, only

temperature control is considered.

The procedure of the strategy is depicted in Fig-

ure 1. The blow line Kappa number is predicted be-

fore the cooking zone - in the middle of the Downﬂow

Lo-Solids

T M

digester (Figure 2). Predicted tempera-

ture and alkali proﬁles of the cooking zone, and on-

line modelled Kappa number proﬁle and process data

ENHANCING KAPPA NUMBER CONTROL IN DOWNFLOW LO-SOLIDSTM DIGESTER USING DIAGNOSIS

AND MODELLING

163

Table 1: Variables for the monitoring system before cooking

zone (BCZ).

Variable Unit

Alkali concentration BCZ g/l (Na

O, EA)

Temperature BCZ K

Production rate BCZ adt/d

Kappa number BCZ

before cooking zone are used as inputs to the Kappa

number prediction model. New temperature set point

is solved iteratively based on the difference between

the predicted and target blow line Kappa numbers.

Also other process conditions, especially alkali pro-

ﬁle, can be more precisely taken into account in the

applied strategy.

3.2 Fault Tolerant Kappa Number

Control Strategy

The fault tolerant control system (see structure in Fig-

ure 3) is formulated by the combination of diagno-

sis and control of the Kappa number in the continu-

ous cooking plant. The self-organizing map (SOM)

is applied for the monitoring purposes. The SOM is

trained with normalized data. The inputs for the mon-

itoring system are presented in Table 1. The quanti-

zation errors are used in the coloring of the trends of

the measured inputs and the predicted Kappa number.

With the aid of the diagnosis part the problematic

process conditions and measurement failures can be

detected. If the process is not in the good operation

area, the control of the Kappa number can be stopped

and keep in the current state for the period of the poor

operation. This ensures that the corrections are not

done into wrong directions and there is not too strong

corrections (overshoot).

Without monitoring problems can occur, due to

the residence time between the cooking tempera-

ture control point (before cooking zone) and on-line

Kappa number measurement. Inaccurate control can

also bring other difﬁculties into the process. One of

the problems is faulty packing in the digester. Faulty

packing can occur, if the chips are cooked too long or

too short a time. Due to the problems, also the shut-

down of the process is possible.

4 CASE STUDY

Case study is Downﬂow Lo-Solids

T M

Kamyr process

consisting of an impregnation vessel and a steam /

liquor phase digester (Figure 2). The chips are im-

pregnated in the impregnation vessel (I1-I2) and in the

K a p p a #

m o d e l

p r e d i c t e d

K a p p a #

T e m p e r a t u r e

a n d a l k a l i

m o d e l s

T + d T

K a p p a #

t a r g e t

n o

y e s

d i f f =

p r e d i c t i o n -

t a r g e t

d T = f ( d i f f )

i s d i f f <

s i g m a 2 ?

T _ s e t p o i n t = T + d T

S O M a n d c o l o r

c o d e s

I s q u a n t i z a t i o n

e r r o r < s i g m a 1 ?

n o

y e s

M e a s u r e d p r o c e s s

d a t a b e f o r e c o o k i n g

z o n e

T _ s e t p o i n t = p r e v i o u s ( T _ s e t p o i n t )

v i s u a l i s e d p r e d i c t e d K a p p a # =

p r e v i o u s ( v i s u a l i s e d p r e d i c t e d K a p p a # )

Figure 3: Structure of the fault tolerant Kappa number con-

trol system.

ﬁrst zone (D1) of the digester. Between upper extrac-

tion and cooking circulation there is a counter-current

washing zone (D2). In this zone, black liquor is dis-

placed with cooking circulation liquor which temper-

ature and alkali concentration are high. The lignin is

mainly removed in the comparatively long co-current

cooking zone (D3). At the bottom of the digester there

is a short washing zone. Softwood chips mainly con-

sist of pine chips with a small amount of spruce chips.

Hardwood chips consist mainly of birch chips with a

small addition of aspen chips.

In Downﬂow Lo-Solids

T M

cooking, the Kappa

number control is mainly performed by the cooking

zone temperature and alkali in the middle of the di-

gester (prior to D3).

In this study, fault tolerant control system is used

for monitoring and control purposes in Downﬂow Lo-

Solids

T M

continuous cooking digester. The inputs to

the system are monitored and the blow line Kappa

number is controlled. The blow line Kappa number

is predicted at the middle of the digester by using

prediction model (Gustafson’s Kappa number model)

and the new temperature setpoint is calculated. The

study is carried out in Matlab environment using mea-

surements from the industrial continuous kraft cook-

ing application.

The monitoring is carried out by using SOM. The

modeling data (about one month data) was collected

from the industrial continuous digester during its nor-

mal operation. The outliers and faulty measurements

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

164

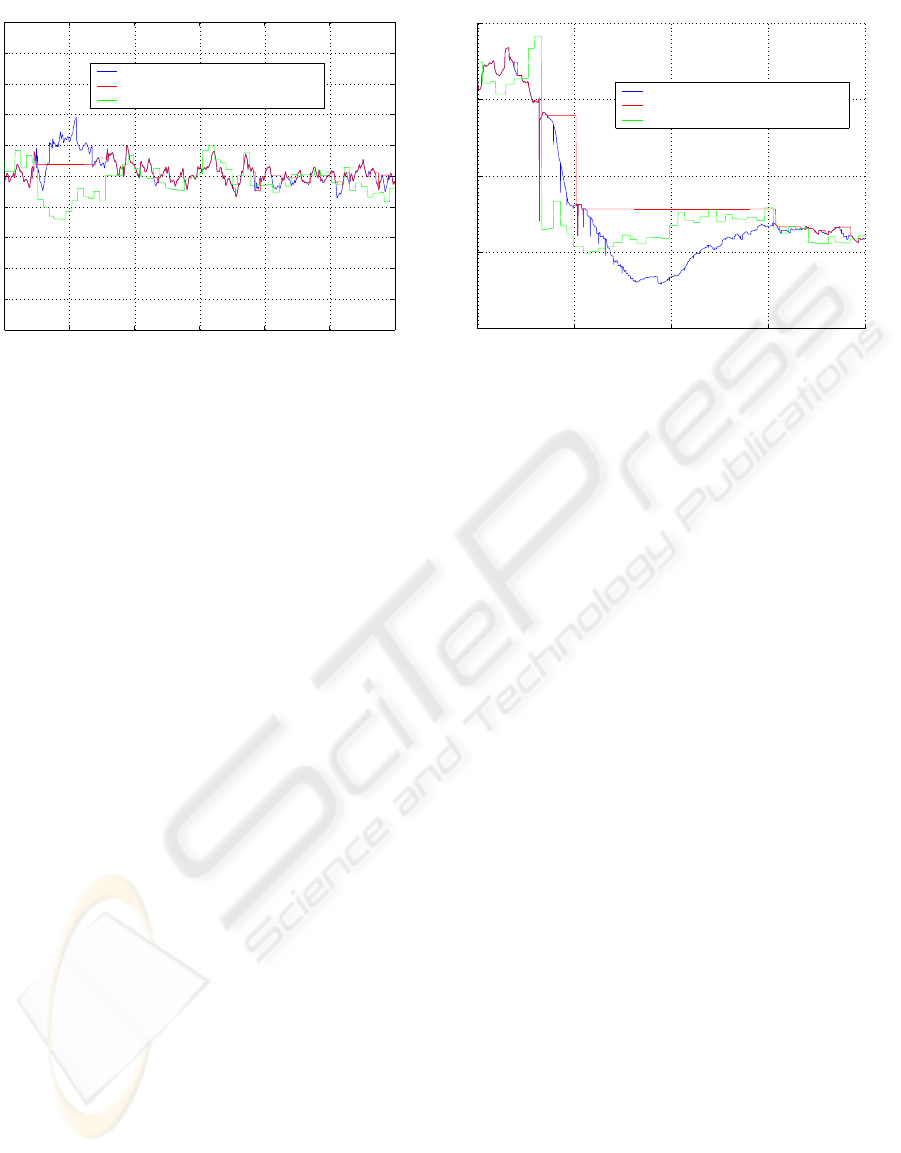
0 500 1000 1500 2000 2500 3000

Validation period 1

Time (min)

Kappa number

Kappa prediction

Kappa prediction with monitoring

on−line Kappa measurement

Figure 4: Validation period 1.

are ﬁltered out from the data. The inputs are tem-

perature, alkali, lignin content (Kappa number) and

production rate before the cooking zone. The system

is validated with the data from the same industrial di-

gester, but from the different time periods.

In the Figures 4 - 6, are presented validation re-

sults of the proposed system. The monitoring system

indicates, whether the prediction can be trusted or not.

The stopping of the prediction is shown in Figure 4 in

the time period 250-750.

Other example is shown in Figure 5, where the

prediction after the grade change has not been good

and it has shifted into wrong direction. The monitor-

ing system has indicated problems in the process and

the prediction has been stopped in time period 600-

1500.

The same kind of example is shown in Figure 6.

The prediction has been stopped for the period 600-

1100.

5 DISCUSSION

The sampling interval of the on-line Kappa number

measurements is about half an hour. Hence, it is use-

ful to also get continuous information about quality

properties. The accurate control can decrease signiﬁ-

cantly problems in the digester. The proposed system

is a combination of diagnosis, prediction and control

of Kappa number in the continuous kraft pulping di-

gester. This kind of systems can be very helpfull for

the operators.

The proposed fault tolerant control system gives

new information for the control and the control ac-

tions are not taken into wrong directions as seen in

Figure 4. In Figure 4 in time step 250-750, the pre-

0 500 1000 1500 2000

Validation period 2

Time (min)

Kappa number

Kappa prediction

Kappa prediction with monitoring

on−line Kappa measurement

Figure 5: Validation period 2.

diction without monitoring is shifted dramatically too

up and the control action would have been too strong

into wrong direction. This has been avoided using

monitoring and the stopping of the prediction.

In the Figures 5 and 6, are shown examples when

there has been problems in the process after the grade

change from softwood to hardwood. Diagnosis sys-

tem has indicated problems and the Kappa number

prediction has been stopped for these faulty periods.

In the validaton period 2 (Figure 5), the prediction is

stopped for the period 600-1500 and in the validation

period 3 (Figure 6) for the period 600-1100.

The approach has been tested using the data

from the industrial Downﬂow Lo-Solids

T M

continu-

ous cooking digester. Although the results are good,

more research is needed to ensure the proper func-

tioning of the proposed system in all operation points.

Both prediction and diagnosis parts need some devel-

opment in the future.

6 CONCLUSION

In this study, the combination of empirical and ex-

perimental methods for the diagnosis and monitoring

of Kappa number control in Downﬂow Lo-Solids

T M

cooking application was considered. Modeling and

prediction of the Kappa number is applied using

Gustafson’s Kappa number model. The SOM is used

to monitor the usability of the modelling and predic-

tion results. The quality control is applied by con-

trolling the temperature at the middle of the digester

(before cooking zone) using diagnosis results and the

prediction of the Gustafson’s Kappa number model.

Good results were achieved using the approach.

ENHANCING KAPPA NUMBER CONTROL IN DOWNFLOW LO-SOLIDSTM DIGESTER USING DIAGNOSIS

AND MODELLING

165

0 500 1000 1500

Validation period 3

Time (min)

Kappa number

Kappa prediction

Kappa prediction with monitoring

on−line Kappa measurement

Figure 6: Validation period 3.

ACKNOWLEDGEMENTS

This research study was funded by The Acedemy of

Finland, Mets

a-Botnia Oy, Andritz Oy, Stora Enso

Oyj, Metso Automation Oy and the Finnish Funding

Agency for Technology and Innovation (Tekes). The

authors would like to thank the partners for the special

knowledge and process data provided.

REFERENCES

Ahvenlampi, T. and Kortela, U. (2005). Clustering algo-

rithms in process monitoring and control application

to continuous digesters. Informatica, 29(1):99–107.

Ahvenlampi, T., Rantanen, R., and Tervaskanto, M. (2006).

Fault tolerant control application for continuous kraft

pulping proces. In 6

IFAC Symposium on Fault

Detection, Supervision and Safety of Technical Pro-

cesses, Beijing, PR China.

Ahvenlampi, T., Tervaskanto, M., and Kortela, U. (2005).

Diagnosis system for continuous cooking process. In

IFAC World Congress, Prague, Czech Republic.

Blanke, M., Kinneart, M., Lunge, J., and Staroswiecki,

M. (2003). Diagnosis and Fault-Tolerant Control.

Springer-Verlag, Berlin.

Dash, S., Rengaswamy, R., and Venkatasubramanian, V.

(2003). Fuzzy-logic based trend classiﬁcation for fault

diagnosis of chemical processes. Computers & Chem-

ical Engineering, 27:347–362.

Gullichsen, J. (2000). Chemical engineering principles of

ﬁber line operations. In Gullichsen, J. and Fogelholm,

C.-J., editors, Chemical Pulping. Papermaking Sci-

ence and Technology, Book 6A. Fapet Oy, Jyv

askyl

Finland.

Gustafson, R. G., Sleicher, C. A., McKean, W. T., and Fin-

layson, B. A. (1983). Theoretical model of the kraft

pulping process. Ind. and Eng. Chem., Process Design

and Development, 22(1):87–96.

Hatton, J. V. (1973). Development of yield prediction equa-

tions in kraft pulping. Tappi J., 56(7):97–100.

Isermann, R. (1997). Supervision, fault-detection and fault-

diagnosis methods - an introduction. Control Engi-

neering Practice, 5(5):639–652.

Kohonen, T. (1997). Self-Organizing Maps. Springer-

Verlag, Berlin, Germany, second edition.

Leivisk

a, K. (2000). Process Control. Papermaking Sci-

ence and Technology, Book 14. Fapet Oy, Helsinki,

Finland.

Mahmoud, M., Jiang, J., and Zhang, Y. (2003). Active

Fault Tolerant Control Systems. Lecture Notes in

Control and Information Sciences. Springer-Verlag,

Berlin, Germany.

Puranen, T. (1999). Jatkuvatoimisen sellukeittimen

airi

ontunnistus sumealla logiikalla (in ﬁnnish). In

Automation’99 -Seminar, pages 406–411, Helsinki,

Finland.

Qian, Y., Li, X., Jiang, Y., and Wen, Y. (2003). An ex-

pert system for real-time fault diagnosis of complex

chemical processes. Expert Systems with Applica-

tions, 24:425–432.

Rantanen, R. (2006). Modelling and control of cooking de-

gree in conventional and modiﬁed continuous pulping

processes. PhD thesis, University of Oulu, Oulu.

Rantanen, R., Ahvenlampi, T., and Kortela, U. (2003).

Kappa number proﬁle in continuous cooking - ap-

plying Gustafson’s model to softwood and hardwood

pulping process. In 4

Biennial Johan Gullichsen

Colloquium, pages 83–92, Espoo, Finland.

Rantanen, R., Simil

a, E., and Ahvenlampi, T. (2005). Mod-

eling of kappa number in Downﬂow Lo-Solids

T M

cooking using Gustafson’s model. Pulp & Paper

Canada, 106(5).

Simani, S. and Patton, R. J. (2002). Model-based data-

driven approach to robust fault diagnosis in chem-

ical processes. In 15th Triennial World Congress,

Barcelona, Spain. IFAC.

Tervaskanto, M., Ahvenlampi, T., Rantanen, R., and Ko-

rtela, U. (2005). Fault diagnosis of continuous cook-

ing process using intelligent sensors. In NeCST Work-

shop, pages 187–192, Ajaccio, France.

Venkatasubramanian, V., Rengaswamy, R., and Kavuri,

S. N. (2003a). A review of process fault detection and

diagnosis part II: Qulitative models and search strate-

gies. Computers & Chemical Engineering, 27:313–

326.

Venkatasubramanian, V., Rengaswamy, R., Yin, K., and

Kavuri, S. N. (2003b). A review of process fault

detection and diagnosis part I: Quantitative model-

based methods. Computers & Chemical Engineering,

27:293–311.

Vroom, K. E. (1957). The h-factor, a means of expressing

cooking times and temperatures as a single variable.

Pulp. Pap. Mag. Can., 58(3):228–231.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

166