TRACKING A WHEELCHAIR WITH A MOBILE PLATFORM
B.Allart, B. Marhic, L. Delahoche, A. Clérentin
Groupe RTeAM of UPJV – IUT Informatique Avenue des facultés – Le Bailly - 80025 Amiens Cedex 1, France
O. Rémy-Néris
CHU of Brest, 5 avenue Foch 29200 Brest
Keywords: Target tracking, Kalman filter, camshift, mobile plateform.
Abstract: This article deals with a target tracking application for th
e disabled. The objective of this work is to track a
wheelchair with a mobile platform and an embedded grasping arm (MANUS). We propose an approach
based on an association of two Kalman filtering levels. The first level permits an estimation of the
wheelchair configuration. The second is used to compute the mobile platform configuration in connection
with its environment. The association of the two filtering process allows a robust tracking between two
objects in movement.
1 INTRODUCTION
In this article we propose an original approach to
solve the problem of configuration estimation of a
target observed by a robot in movement. We propose
a probabilistic approach based on Kalman Filtering.
The problem of tracking is classical in the world of
robotics. It’s generally linked to the data association
stage. The data association problem is that of
associating the many measurements made by a
sensor with the underlying states or trajectories that
are being observed. It includes issues of validating
data, associating the correct measurement to the
correct states or trajectories, and initializing,
confirming or deleting trajectories or states. This
way, the Probabilistic Data Association Filter
(PDAF) (Y. Bar Shalom et T.E. Fortmann, 1988) for
single targets and the Joint Probability Data
Association Filter (JPDAF) (Y. Bar Shalom et T.E.
Fortmann, 1988 and Bar-Shalom Y, Xiao-Rong
Li,1995) for multiple targets are two inescapable
approaches. They are both Bayesian algorithms that
compute the probability of correct association
between an observation and a trajectory. We can
combine the Sequential Monte Carlo method to
decline the JPDAF method.
A second classical paradigm of data association is
th
e Multiple hypothesis tracking (MHT) which
permits to represent multimodal distributions with
Kalman filters (Y. Bar Shalom et T.E. Fortmann,
1988). It has been used with great effectiveness in
radar tracking systems, for example. This method
maintains a bank of Kalman filters, where each filter
corresponds to a specific hypothesis about the target
set. In the usual approach, each hypothesis
corresponds to a postulated association between the
target and a measured feature.
For our application, we have made the choice to
u
se two Kalman filters to solve the problem of
tracking between two objects in movement.
In a first part we present the used perception
syste
m, which permits to track the wheelchair that is
to say a stereo omnidirectional sensor.
In a second part, we address the problem of
wh
eelchair recognition using vision sensors.
In the third part, we deal with the multi-level
Kalm
an filtering tracking.
We conclude with an explanation of experimental
resu
lts.
2 THE MOBILE PLATFORM
2.1 Context Overview
This work deals with technical assistance for persons
of reduced mobility. The mobile platform is built
with a wheelchair frame. The reader interested by
306
Allart B., Marhic B., Delahoche L., Clérentin A. and Rémy-Néris O. (2007).
TRACKING A WHEELCHAIR WITH A MOBILE PLATFORM.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 306-311
DOI: 10.5220/0001626403060311
Copyright
c
 SciTePress

this robotic assistance can find details in (B. Marhic,
L. Delahoche ,F. de Chaumont, and O. Remy-Néris,
2006).
The SPI group of the IUT of Amiens has applied
its skills in the domains of mobile robotics and
detection of the surrounding environment. It is
involved in the integration of a system of detection
via a motorised platform that can be mounted by a
grasping arm MANUS
(R)
.
2.2 Sensors Involved in this Paper
2.2.1 Dead Reckoning and its Uncertainty
We are going to establish the discontinuous
equations of the platform position considering small
displacements (Figure 1)
Figure 1 : Displacement of the robot during a period.
We thus obtain:
qn qn qn( ) () ()
+
=+1 Δ
where q is the position of the mobile platform.
In which:
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+⋅⋅
+⋅⋅
=Δ
)(
)2/)()(sin(
2/)(
)2/)(sin(
)(
)2/)()(cos(
2/)(
)2/)(sin(
)(
)(
n
nn
n
n
nS
nn
n
n
nS
nq
δθ
δθθ
δθ
δθ
δ
δθθ
δθ
δθ
δ
(2)
The vector from the equation (2) which is exact,
can be simplified if we consider that the sampling
period is small enough (sin(δθ (n)/2)/ (δθ (n)/2))≈1.
Thus (order 0),
(3)
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⋅
=Δ
δθ
θδ
θδ
))(sin(
))(cos(
)( nS
nS
nq
The sampling period being very small, it is
possible to assimilate the elementary displacement
to a segment. Therefore we will use the development
to the order 0 (3), into the following calculations:
()
()
⎪
⎩
⎪
⎨
⎧
+=+
⋅+=+
⋅+=+
)()()1(
)(sin)()()1(
)(cos)()()1(
nnn
nnSnYnY
nnSnXnX
odoodo
odoodo
δθθθ
θδ
θδ
(4)
With the matrix form, we obtain (F is a non-linear
function in q):
(
)
qn Fqn n
nSnn
t
() (),(
() [ (), ()]
+=
=
1 Δ
Δ
δδθ
)
(5)
)(
ˆ
)()( nBqnn
mes
Δ=+Δ=Δ
Bq ~ N(0,V
bq
) (Gaussian noises, centred)
We will apply the Taylor development of F
(equation 5) around
(
)
)1(
ˆ
),1(
ˆ
−Δ− nnq
, in order to
render the equations linear.
2.2.2 Stereoscopic Omnidirectional Vision
System
On the figure 2, we can see the configuration of the
two omnidirectional vision sensors.
The Manus®
arm
The two omnidirectional
vision sensors
Figure 2: The mobile platform.
Main vision applications in mobile robotics use
the classical pinhole camera model. Thus according
to the lens used, the field of view is limited.
Nevertheless, it is possible to enlarge the field of
view by using cameras mounted in several directions
(H. Ishiguro, S. Tsuji, 1993), but the information
flow is very important and time consuming. Other
applications (E. Colle, Y. Rybarczyk, P. Hoppenot,
2002) use only one camera, with a rotation motion,
in order to sweep a large space. The disadvantage of
such a system is that the camera’s movement takes
time; and what’s more, a mechanical looseness can
appear in the course of time. To get wide-angle
pictures, another possibility exists: omnidirectional
vision. These kinds of sensors allow acquiring
scenes with 360° field of view (El. M. Mouaddib, B.
Marhic, 2000). There are two major classes of
omnidirectional vision systems. First of all, systems
TRACKING A WHEELCHAIR WITH A MOBILE PLATFORM
307

made of a mirror and a camera, are called
“catadioptric systems” (C. Cauchois, E. Brassart, L.
Delahoche, T. Delhommelle, 2000)( H. Ishiguro, S.
Tsuji, 1996). The second one is composed of a
classical camera with a fish-eye lens; such
mountings are called “dioptric systems” (Z. L. Cao,
S. J. Oh, Ernest L. Hall, 1986). We focus on the first
class.
There are many advantages to using an
omnidirectional vision sensor. Firstly, in one
acquisition, we obtain a full view of the environment
without using a sophisticated mechanical system.
Secondly, even if the interpretation of
omnidirectional pictures is difficult for novices, we
can easily compute a “classical perspective view” of
the scene. Finally, providing a picture in a chosen
direction is instantaneous.
The omnidirectional vision system we use is
made of a digital color video camera and a
hyperbolic mirror. Figure 3 shows an
omnidirectional view of an environment with a
wheelchair in the field of view.
a wheelchair
Figure 3: (left) an omnidirectional view of a scene with a
wheelchair in the field of view. (right) “un-warped”
picture of the white area from the omnidirectional view.
3 TRACKING RECOGNITION
3.1 Initialisation (Target-wheelchair)
We wished to achieve the greatest possible degree of
flexibility regarding the use of the robotised
assistance. We therefore did not want to restrict our
method to the use of one wheelchair in particular.
Our construction of the model accommodates not
only the wheelchair, but also the patient. This is why
we turned our work towards an intrinsic polymorph
(self re-configuring), directly calculated from a
stereoscopic colour video signal. The figure below
(Figure 4) shows omnidirectional images: they
illustrate the extraction of the background and the
extraction of the wheelchair.
Figure 4: Target Initialisation.
Once the model is computed, a histogram
representation is calculated.
3.2 The OmniCAMShift Recognition
and Triangulation
As the wheelchair is not equipped with any
particular marker, we have to track it as it is. This
way, we use the CAMShift algorithm, which
performs a tracking, by using an image of the object
to track. The Continuously Adaptive Mean Shift
(CAMShift) algorithm (C. Cauchois, E. Brassart, L.
Delahoche, T. Delhommelle, 2000), is based on the
mean shift algorithm (B. Marhic, L. Delahoche ,F.
de Chaumont, and O. Remy-Néris, 2006), a robust
non-parametric iterative technique for finding the
mode of probability distributions including
rescaling.
We have named “Omnicamshift” the calculation
of a CAMShift directly in an omnidirectional image.
We have also applied some specificity linked to the
sensor used (fast gyration, …). The next figure
(Figure 5) shows an example of the OmniCAMShift
application:
Previous Location
Estimated Location
Final Location
Estimated gyration
Computed Angle
for the triangulation
Figure 5: Wheelchair recognition using OmniCAMShift.
Once the wheelchair is identified in both
omnidirectional images, computing the relative
position of the wheelchair by triangulation is a
minor task (Figure 6) :
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
308

2)tan()tan(
)tan(
d
ab
bd
x +
−
×
=
)tan()tan(
)tan()tan(
ab
abd
y
−
××
=
Figure 6: triangulation.
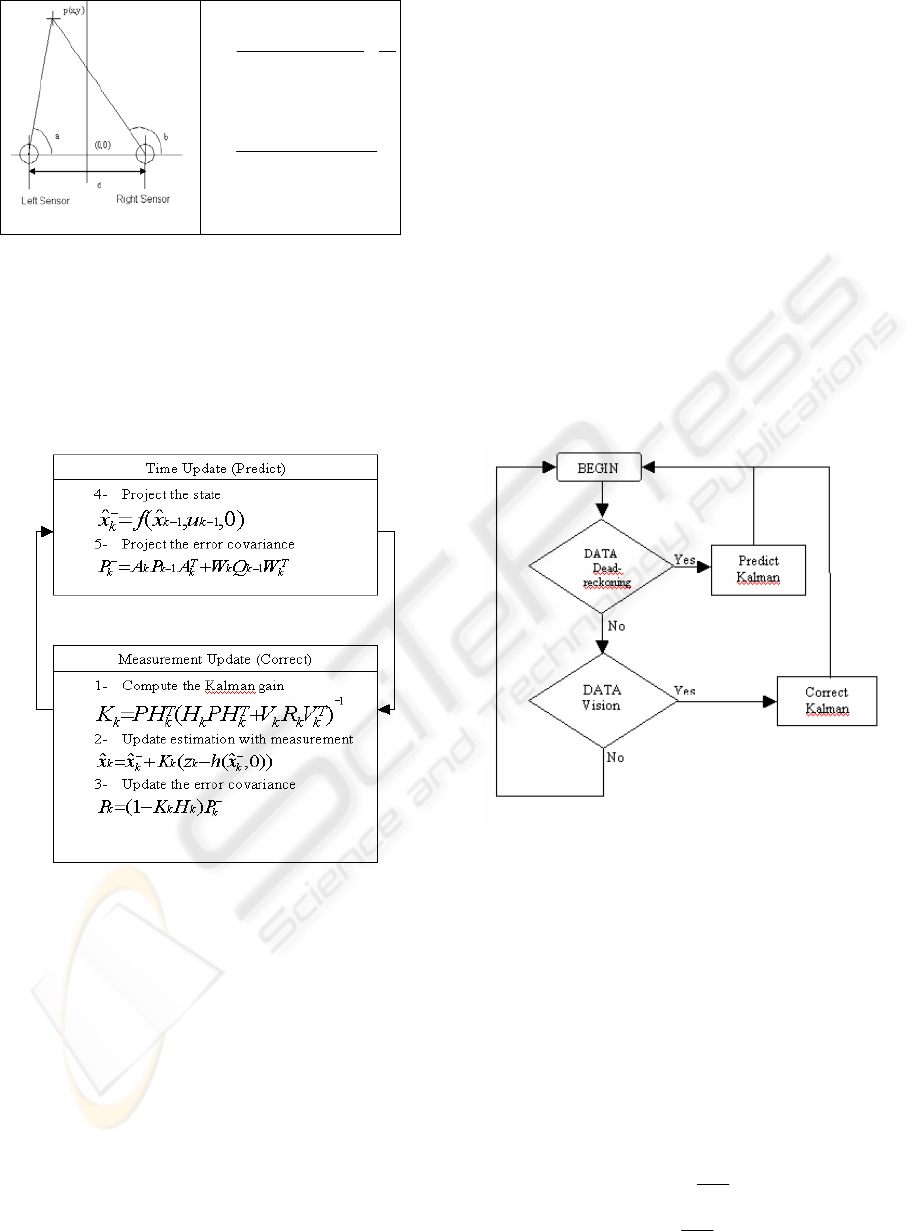
4 TRAKING WITH KALMAN
FILTER
4.1 The Kalman Filter
Figure 7: Kalman filter.
We would like to recall at this point that the
process that manages the movement of the RMA is
discontinuous and non linear in θ. The
measurements Y(n) are linked to q(n) by an equation
of observation (or equation of measurement).
(6)
()
[]
qn Fqn n v
nSnn
Yn H qn w
t
() (),()
() (), ()
() ()
+= +
=
=⋅ +
1 Δ
Δ
δδθ
with :
Ö v is a centred Gaussian white noise, of the
variance matrix Cpro.
Ö w is a Gaussian white noise which
perturbs the measurement.
Ö Δ(n) is the vector of command.
Ö q(n) is the trajectory of the state vector,
representing the localisation of the mobile
platform.
Ö H is the observation matrix.
4.2 Filtering with Non-inner
Observation
In this application, we have two objects in
movement, a wheelchair and a mobile platform.
However, we only have proprioceptive movement
information on the mobile platform. Using dead-
reckoning we compute the position of our mobile
platform and using the omnidirectional vision
system (exteroceptive), we calculate the relative
position of the wheelchair compared to our mobile
platform.
Figure 8: Filter’s algorithm.
From the implementation of our model, we
decided to use for the prediction of the Kalman filter
the data give by the odometric sensor and for the
step of update the data give by triangulation of the
two omni-directional sensor.
We decide to make the triangulation operation out
of your filter and injected directly the result in the
update step of kalman filter. That makes it possible
to bring us back to a linear system.
The vision module permits to obtain
[
]
t
ff
yxXf =
, where :
tri
n
nnodof
XDXX +
Δ
+Δ+=
−−
)
2
cos(*
11
θ
θ
(7)
tri
n
nnodof
YDYY +
Δ
+Δ+=
−−
)
2
sin(*
11
θ
θ
(8)
TRACKING A WHEELCHAIR WITH A MOBILE PLATFORM
309

with Xtri and Ytri the position between the mobile
platform and the wheelchair and, X
odo
and Y
odo
the
result of odometric equations .
In order to have a homogeneous filtering, the
vision uncertainty of the localisation is considered to
be a Gaussian white noise.
Thus, we obtain :
IH
wXfY
=
+=
“I” being the identity matrix.
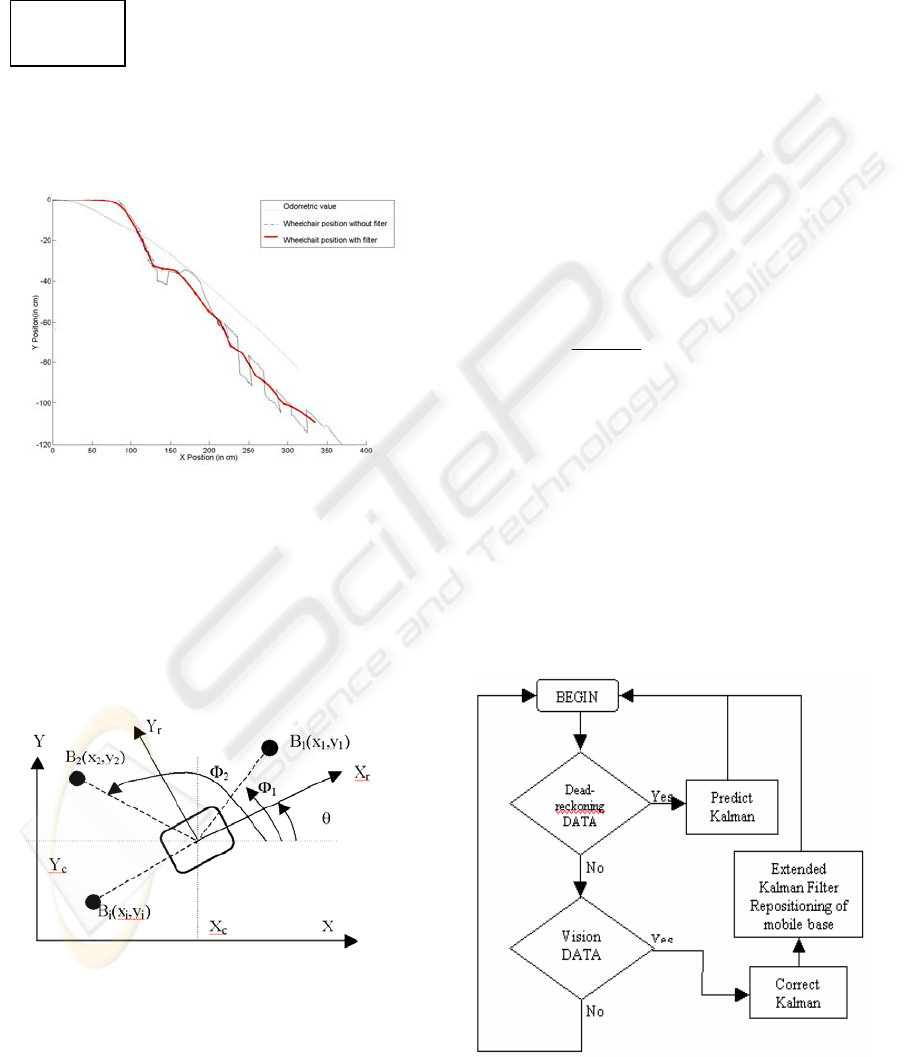
The result obtained was satisfactory for straight
lines (figure 9) but insufficient during the phase
where the mobile platform turned due to errors of
odometry.
Figure 9: Filter with a good precision.
4.3 Extended Filtering
To remove the problem of the imperfection of the
dead-reckoning, we will use a method which
requires a knowledge of the landmarks. We will be
able to determine with precision, the position of our
mobile plateform and to thus replace it to avoid the
errors of the dead-reckoning.
Figure 10: Relation between beacon and mobile platform.
For us, these landmarks are walls, doors, objects,
angles which one will be able to detect in an
omnidirectional image. Therefore, it is necessary for
us to know the map of the environment to be able to
mark it out.
Moreover, this method is based on an extended Kalman
filter that can be integrated into our preceding process.
For this process, the equation of observation of
the extended Kalman is as follows.
The vector of observation is written:
kkk
k
k
k
k
vkXhv
n
z +=+
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
= ),(
.
.
2
1
*
τ
τ
τ
(9)
where is the layer of i
τ
k
i
ème
beacon BB
i
of co-
ordinates (x
i
, y
i
) i the world landmark in the moment
k. And v
k
is a measurement noise, presumably white
and Gaussian.
The exact position of the beacon B
i
is expressed
according to the state vector X
k
of the system as
follows
:
)arctan(
ik
ik
k
xx
yy
i
−
−
=
τ
(10)
The matrix of the Jacobien of the vector function
H is, in the case of measurements of absolute angle:
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−−−−
−−−−
−
=
=
0/)(/)(
...
0/)(/)(
22
2
11
2
11
1/
ˆ
knnkknk
kkkk
H
dxxdyny
dxxdyy
kkk
XX
k
(11)
where d is the distance between the landmark
and the mobile platform
Figure 11: Process of filtering.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
310

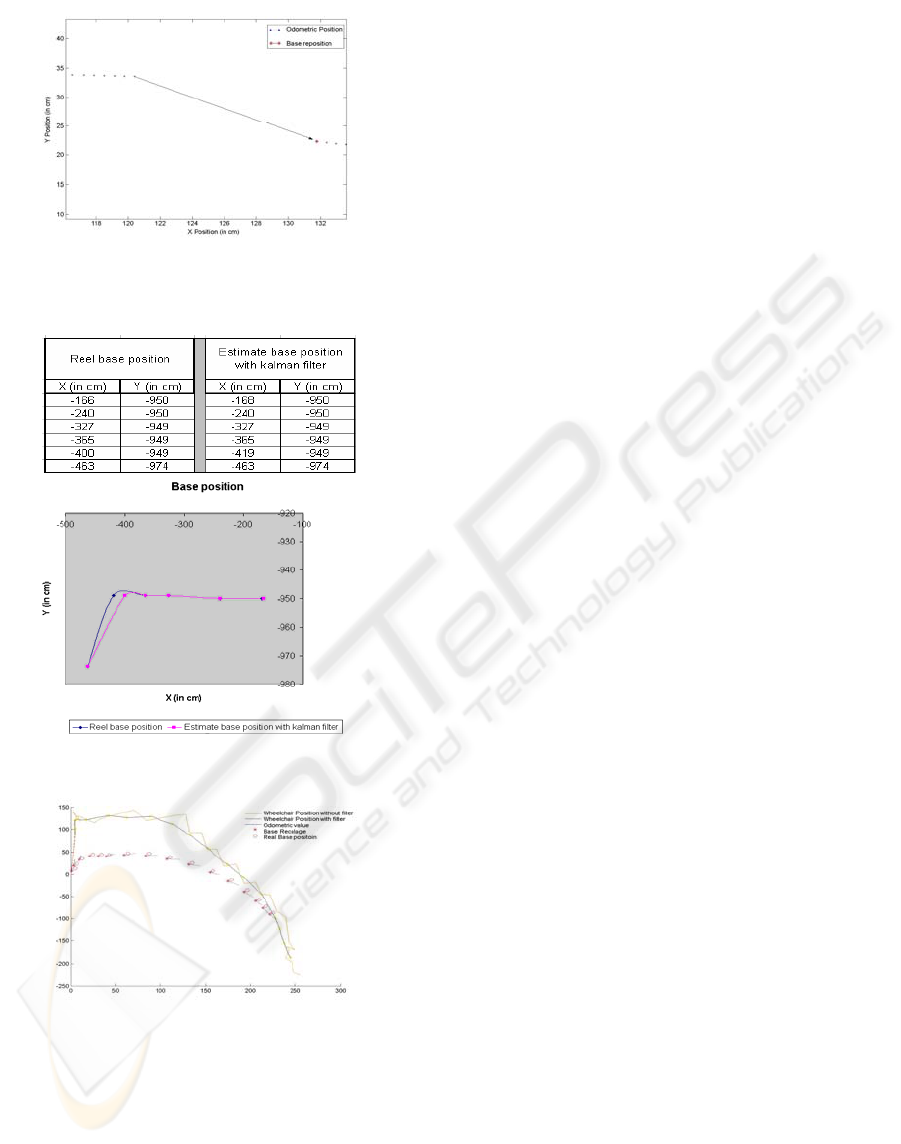
Figure 12: Repositioning of the mobile platform.
Table 1: Data after simulation of the system.
Figure 13: System’s result.
Figure 14: Other Result of the application.
With this method, we clearly see a marked
improvement of the localisation, especially when the
mobile platform turns. (Figure 12) which enabled us
to improve the precision of our system (Table 1,
Figure 13 where we can see the result of the system
in a right line and Figure 14 which is the system’s
result in a turning).
5 CONCLUSION
In this article, we studied a target tracking
application for the physically disabled. The aim is to
track a wheelchair with a mobile platform mounted
with a grasping arm (MANUS). We propose an
approach based on an association of two Kalman
filtering levels. The first level permits to estimate the
wheelchair configuration. The second is used to
compute the mobile platform configuration in
connection with its environment. We have shown
that the second level increases the robustness of the
configuration estimation of the wheelchair in the
platform frame. The use of the identity matrix in the
first stage of the Kalman filtering permits to solve
the problem of the non-linearity of the system.
This paradigm can be a contribution to finding a
solution for tracking several objects in movement.
The robustness of the filtering process is very
important. Future works will study the integration of
a supplementary layer based on a particle filter.
REFERENCES
Z. L. Cao, S. J. Oh, Ernest L. Hall. Omnidirectional
dynamic vision positioning for a mobile robot”
Journal of Robotic System, 3(1), 1986, pp5-17.
C. Cauchois, E. Brassart, L. Delahoche, T. Delhommelle.
“Reconstruction with the calibrated SYCLOP sensor”
in Proc, Int. Conf. on Intelligent Robots and Systems,
Kagawa University, Takamatsu, Japan , pp. 1493-
1498, October- November 2000.
E. Colle, Y. Rybarczyk, P. Hoppenot. “ARPH: An
assistant robot for disabled person” in Proc. IEEE
International Conference on Systems, Man and
Cybernetics, Hammamet, Tunisia, October 6-9, 2002.
H. Ishiguro, S. Tsuji “Applying Panoramic Sensing to
Autonomous Map Making a Mobile Robot” in Proc,
Int. Conf. on Advanced Robotics, pp127-132,
November 1993.
H. Ishiguro, S. Tsuji “Image-based memory of
environment” in Proc, Int. Conf. on Intelligent Robots
and Systems, pp634-639, Osaka, Japan, November
1996.
El. M. Mouaddib, B. Marhic, “Geometrical Matching for
Mobile Robot Localisation”. IEEE Trans. Robotics
and Automation, vol. 16, n°5, pp 542-552, October
2000.
B. Marhic, L. Delahoche ,F. de Chaumont, and O. Remy-
Néris, “Robotised Assistance for Persons of Reduced
Mobility: résumé of a project”, ICOST’2006, Ireland.
Y. BAR SHALOM et T.E. FORTMANN, "Tracking and
data association", Academic Press, 1988.
Bar-Shalom Y, Xiao-Rong Li, Multitarget-Multisensor
Tracking: Principles and techniques, 1995.
TRACKING A WHEELCHAIR WITH A MOBILE PLATFORM
311