DISTURBANCE FEED FORWARD CONTROL OF A HANDHELD

PARALLEL ROBOT

Achim Wagner, Matthias N

ubel, Essam Badreddin

Automation Laboratory

University of Mannheim, D-68131 Mannheim, Germany

Peter P. Pott, Markus L. Schwarz

Laboratory for Biomechanics and experimental Orthopaedics, OUZ

Faculty of Medicine Mannheim, University of Heidelberg, Germany

Keywords:

Robotic manipulators, Medical systems, Dynamic modelling, Disturbance rejection, Feedforward compensa-

tion.

Abstract:

A model-based control approach for a surgical parallel robot is presented, which combines a local tool stabi-

lization with a global disturbance feed forward control. The robot is held in the operator’s hand during the

manipulation of bones. For a precise processing the tool has to be decoupled from disturbances due to unin-

tentional hand movements of the surgeon at the robot base. The base disturbances are transformed for a feed

forward control using the inverse dynamics of the robot. Simulations show that disturbances can be reduced

by many orders depending on sensor errors and delay.

1 INTRODUCTION

Parallel robots are widely used, where high stiff-

ness, high dynamics or low error propagation over

the kinematic chains is required, e.g. ﬂight sim-

ulators (Koekebakker et al., 1998), processing ma-

chines (T

onshoff et al., 2002), positioning and stabi-

lization platforms (Huynh, 2001), vibration isolation

(Chen and McInroy, 2004) and medical manipulators

(Pott et al., 2004; Wagner et al., 2004). The prob-

ably most famous Hexapod parallel kinematic struc-

ture is the Stewart-platform (Stewart, 1966) which has

six degrees-of-freedom (DOF). An obvious advantage

considering hand-held applications is, that a parallel

robot has high potential for a lightweight construc-

tion. By ﬁxing the most massive part of the actu-

ators to base (Merlet, 2000), the actively positioned

mass can be further decreased. This leads to a re-

duction of static and dynamic forces (Honegger et al.,

1997; Huynh, 2001). The forces of the actuators can

be transferred to the tool platform using light struts.

Within the hand-held surgical robot project ”Intelli-

gent Tool Drive” (ITD), a parallel robot is designed

to align a milling tool relatively to a moving bone

of the patient (workpiece) and to decouple the tool

from unintentional hand movements at the base. The

standard procedure to control a parallel manipulator

is transforming the desired tool motion into the de-

sired leg motion with the inverse kinematics and con-

trolling the leg motion separately on the axes level

onshoff et al., 2002). However, if high dynamics

is required this simple kinematics approach does not

lead to a high precision tool pose control, especially

if the robot’s base is freely movable. Therefore, full

dynamic models of special parallel robots are intro-

duced to improve the quality of a fast platform control

(Riebe and Ulbrich, 2003; Honegger, 1999). The non-

linear inverse dynamic large-signal model for a paral-

lel robot with two movable platforms is introduced in

(Wagner et al., 2006). This model is used here to con-

trol the pose of the tool, while it is decoupled from

base disturbances. Since the robot is movable freely

in space adequate co-ordinate systems must be de-

ﬁned. The local control of the tool is performed in

the base instantaneously coincident reference frame

using the inverse kinematics description of the robot.

The same reference frame can be used to achieve a dy-

namic feed forward compensation. However, for the

compensation of the gravity inﬂuences and for a ab-

solute position referencing a world coordinate system

must be deﬁned. In the following sections the control

structure and simulations are presented to show the

advantages and drawbacks of the approach.

Wagner A., Nübel M., Badreddin E., P. Pott P. and L. Schwarz M. (2007).

DISTURBANCE FEED FORWARD CONTROL OF A HANDHELD PARALLEL ROBOT.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 44-51

DOI: 10.5220/0001626500440051

 SciTePress

2 SYSTEM DESCRIPTION

The goal of the ITD robot project is to adjust and

to stabilize a drilling or milling tool (mounted at the

tool platform) with respect to a moving bone of the

patient (workpiece), while the complete machine is

held in the surgeon’s hand. Therefore it is necessary

to isolate the tool from disturbances at the base pro-

duced by the operator’s unintional hand movements.

The amplitude and frequency of the human arm dis-

turbances is available from literature (Takanokura and

Sakamoto, 2001). Corresponding to the milling pro-

cess with different tools a 6 DOF control of the tool

is required. Assuming an additional safety margin the

selected workspace of the robot ranges from -20 mm

to +20 mm in the three Cartesian axes and respec-

tively from -20

to +20

in the three rotational axes.

The mechanical device designed is a parallel robot

with six base-ﬁxed actuators. The CAD model of

the surgical robot ITDII (Intelligent Tool Drive II) is

shown in Fig. 1. The robot base has six ﬁxed linear

motors, i.e. the electrical part of the motors. Further-

more, there are guide rails, housing, and handles for

the hand-held operation, building together the robot

base. The sliders of the linear motors are connected

to the tool platform via six lightweight struts. At the

tool platform and at the sliders the struts are mounted

with spherical joints.

Because the base of the robot can be moved freely

Figure 1: Hand-held surgical robot ITDII - CAD model.

s,i

st,i

t,i

{W}

{T}

{B},{B }’

tool

platform

baseplatform

actuatori

slideri

struti

Figure 2: Topology of the parallel robot with ﬁxed actua-

tors.

in space, adequate coordinate systems have to be de-

ﬁned. For the calculation of the kinematic equations

four coordinate frames are considered (Fig. 2): (1)

the world (earth) frame {W}, (2) the tool frame {T}

in the tool’s centre of gravity, (3) the movable base

frame {B} in the base’s center of gravity, and (4) the

instantaneously coincident base frame {B’}, which is

ﬁxed in {W}. The frame {B’} and the frame {B} are

aligned, if the base stands still. Without loss of gen-

erality the motion of both platforms is represented in

the {B’} frame, which reduces the complexity of the

kinematic description. The choice of the coordinates

has no inﬂuence on the value of the inertial forces.

For simplicity the gravity is calculated in the world

frame. Afterwards, the resulting force can be trans-

formed into the {B’} frame with little effort.

The pose of the tool is deﬁned by the position

vector

and the orientation matrix

R in the {B}

frame, which build together the pose vector

(

R). From the matrix

R the ﬁxed zyx-Euler

angles φ, θ, and ψ can be derived. The positions of

the tool joints

t,i

in the tool frame and the initial po-

sitions of the slider joints

in the base frame for

each actuator i are known from the geometry of the

construction. The sliders actual positions

s,i

move

in z-direction of the base according to the guidance,

if the tool changes its position. Therefore, the initial

positions

s,i,x

,i,x

and

s,i,y

,i,y

in the

x-direction respectively the y-direction are not alter-

nated. The struts have the lengths l

DISTURBANCE FEED FORWARD CONTROL OF A HANDHELD PARALLEL ROBOT

3 MODELLING

For the model-based control of the robot, the non-

linear inverse dynamic description is required, espe-

cially if both platforms can be moved freely in the

entire workspace.

3.1 Inverse Kinematics

The inverse kinematics of the robot describes the non-

linear relationship between the relative tool-base pose

and the slider positions, which states the operating

point of the robot in the instantaneously coincident

base frame {B’}. Furthermore, the velocities and ac-

celerations of the sliders are given from the relative

motion of the tool and the base in {B’}.

3.1.1 Pose

Since the slider positions are constrained by the six

struts i = 1..6, the joint x and y distances between

slider and strut joints are given by

st,i,x

s,i,x

−

t,i,x

(1)

and

st,i,y

s,i,y

−

t,i,y

. (2)

With the assumption of constant strut lengths l

the

z-component of the joint distance vectors can be cal-

culated as

st,i,z

− (

st,i,x

)

− (

st,i,y

)

(3)

and the slider joint positions yield

s,i,z

t,i,z

st,i,z

. (4)

The required shift of the actuator positions with re-

spect of the starting positions

,i,z

s,i,z

−

,i,z

, (5)

which is measured by local positioning sensors.

3.1.2 Velocity

The generalized tool and base velocities

′

= (

′

) and

′

= (

′

) em-

brace the translational velocities

′

respectively

′

and the angular velocities

′

and

′

of both

rigid bodies. According to a rigid body motion the

tool joint positions and the base-ﬁxed initial slider

joint positions can be determined from the general-

ized velocities. Due to the constant strut lengths, the

z-components of the relative slider velocities

′

st,i,z

= −

st,i,x

st,i,z

′

st,i,x

−

st,i,y

st,i,z

′

st,i,y

(6)

result from the constraint movement on a sphere with

radius l

. The relative velocities of the sliders, which

can be measured and controlled on the actuator level,

˙q

′

st,i,z

′

t,i,z

−

′

s,i,z

(7)

with the tool joint velocities

′

t,i,z

and the velocities

of the initial joint positions

′

s,i,z

3.1.3 Acceleration

Corresponding to the velocity derivation, the gener-

alized accelerations of the tool and the base are de-

ﬁned by

′

= (

′

) and

′

= (

′

)

with the translational accelerations

′

and

′

and

the angular accelerations

′

and

′

. The acceler-

ations of the joints are assemblies of three terms: (1)

inertial acceleration a

′

, 2) centripetal acceleration a

′′

and (3) Coriolis acceleration a

′′′

. The inertial terms of

the slider joints are

′

s,i

′

s,i

, (8)

and the centripetal accelerations are

′

′′

s,i

′

s,i

. (9)

The Coriolis acceleration terms are non-zero in x-

direction

′

′′′

s,i,x

= 2·

′

B,y

· ˙q

(10)

and in y-direction

′

′′′

s,i,y

= − 2·

′

B,x

· ˙q

. (11)

The z-component

′

′′′

s,i,z

is identical zero.

Summarizing the three terms, the slider joint ac-

celerations in x and y direction result in

′

s,i,x

′

s,i,x

′

′′

s,i,x

′

′′′

s,i,x

(12)

′

s,i,y

′

s,i,y

′

′′

s,i,y

′

′′′

s,i,y

. (13)

The slider acceleration in z-direction is not a simple

sum, because the slider motion is constrained by the

struts according to the sphere equation

′

st,i,z

= −

st,i,x

st,i,z



′

st,i,x

′

nst,i,x



−

st,i,y

st,i,z



′

st,i,y

′

nst,i,y



−



′

nst,i,z



(14)

with the normal acceleration

′

nst,i

= −



st,i

′

st,i



′

st,i



st,i



(15)

Finally, the slider joint accelerations are

′

s,i,z

′

st,i,z

′

t,i,z

. (16)

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

and the acceleration of a slider’s center of gravity

yields

′

cg,i,z

′

s,i,z

′

scg,i

(17)

with the position offset

scg,i

between the slider joint

position and the slider’s centre of gravity.

3.2 Inverse Dynamics

The inverse dynamics of the robot describes the actu-

ator forces needed to move the tool’s centre of gravity

with a desired velocity and acceleration. Additionally,

the actuator forces are derived to stabilize the tool, if

the base is disturbed. In this section a brief sketch of

the ITDII robot’s inverse dynamics is given. A more

detailed description can be found in (Wagner et al.,

2006).

The rigid body dynamics of a parallel robot can be

described generally by the equation of motion

′

= M(q) ·

q+ C(q,

q) ·

q+ G(q). (18)

with the generalized force

′

, which is necessary to

move the tool platform in a ﬁxed frame {B’}. Within

this equation M is the generalized mass matrix, C is

the centripedal and Coriolis component and G is the

gravity component of the platform. These parameters

depend on the operationg point of the robot. The gen-

eralized force is converted into actuator forces using

the Jacobian matrix of the robot. Additionally, the in-

ertia forces

s,i

= m

s,i

′

cg,i,z

−





. (19)

are taken into acount with the slider masses m

s,i

. The

gravitiy vector g = (0 0 − 9, 81m/s

)

can be trans-

formed from the {W} frame into the {B} frame using

the rotation matrix

R. Since the major part of the

strut masses is concentrated in the joints and since the

link beetween the joints is lightweight, the struts can

be separated into two parts, which can be added to the

slider and tool components (Honegger, 1999). Corre-

spondingly the strut masses and inertias are not con-

sidered in the inverse dynamics explicitly. In a ﬁrst

attempt the friction forces are neglected as well. The

latter can easily be extended on the actuator level, if

necessary. The non-working reaction forces/torques

of the actuators are perpendicular to the actuator mo-

tions and, therefore, not considered in the robot dy-

namics.

For the calculation of all force components the rel-

ative velocity and acceleration between the tool and

the base as well as the absolute orientation of the robot

in the world coordinates must be available. It should

be mentioned, that the actuator forces are not simple

vector sums of the tool and the base related forces,

since the equation of motion is non-linear. However,

if the tool is ﬁxed, the

′

term vanishes and the re-

maining forces for the slider mass acceleration yields

a quite simple form (19).

4 CONTROL STRUCTURE

The robot control must be suited to adjust the tool

against a movable workpiece and to decouple the tool

from disturbances at the base. Therefore, a control

structure was designed, which combines a servo con-

trol on the local axis level with a disturbance feed-

forward control in the global Cartesian space (Fig. 3).

For the controller design the adequate choice of

co-ordinate systems is essential, since the complete

robot can be moved freely in space and the component

inertia forces are related to a earth ﬁxed (respectively

inertia) reference system. The local stabilization is

based on the robot kinematics, which describes the

relative pose between tool and base in relation to the

actuator positions. Here, the actuator position are not

dependent on the tool and base reference. In contrast,

the feed-forward control uses the inverse dynamics

block, which is deﬁnded in {B’}. The sensor sig-

nals for the base pose, velocity and acceleration are

retrieved in the world frame. Furthermore, the de-

sired tool motion is given in the world frame as well.

Therefore, the tool and base motion signal are con-

verted to {B’} co-ordinates before they are applied to

the inverse kinematics. This geometric transforma-

tion can be done with little effort.

The local control is based on the slider position

and velocity sensor signals q and

q. The actuator sig-

nals are compared to the desired actuator signals q

and

. Using the generalized tool mass matrix M a

PD-controller generates the force signals F

needed

to stabilize the tool. The reference signals q

and

result from the desired tool signals

, and

and from the actual base coordinates

, and

both in Cartesian world coordinates, using the inverse

kinematics of the parallel robot.

The feed-forward control block consists of two

inputs, the tool reference signals

, and

and the actual base signals

, and

. Using the inverse dynamic model the feed-

forward forces F

are calculated which are required

to move the tool as desired, while the disturbances

from the base are canceled. If the inverse dynamic

model and the sensor/actuator signals are assumed to

be perfect, the local control error will be zero. How-

ever, the inverse model is not really complete due to

the neglected strut masses, actuator friction and un-

DISTURBANCE FEED FORWARD CONTROL OF A HANDHELD PARALLEL ROBOT

Figure 3: Control structure; local servo loop and global disturbance feed forward control.

measured disturbances. These model uncertainties

are compensated by the local pose control. The pre-

sented structure is not a classical cascaded structure,

because the base coordinates are not inﬂuenced im-

mediately by the control action. The base motion re-

sults from the disturbance forces of the human opera-

tor. That means that no feed-back from the actuators

to the base motion is assumed due to the large base

mass and that the sensing of the base motion serves

for the referencing of coordinates only.

In the realized system it is necessary to measure

the pose, the velocity and the acceleration of the base.

The tool coordinates are calculated from the desired

tool trajectory. To take care of force feed-back dur-

ing the processing of the workpiece, additional sen-

sors measuring the tool motion or forces could be im-

plemented in a feed-back control. This may make

sense in special cases. However, backlash effects in

the joints could lead to a destabilization of the con-

trolled system. Therefore, and for the sake of sim-

plicity we are content with the local stabilization.

As shown in literature (Riebe and Ulbrich, 2003),

a friction compensation is essential in the real appli-

cation, which can be added on the local axis level. To

separate the kinetic effects from the friction effects,

such a compensation is neglected in this paper. The

control structure has been implemented in the simula-

tion environment Matlab/Simulink using a ﬁxed sam-

pling time of 1 ms. As a consequence the minimum

delay in the control loop is 1 ms as well. The forward

dynamics of the robot ITD used in the closed loop

simulations has been modelled with the SimMechan-

ics toolbox.

5 SIMULATION

The simulations presented in this section mainly sup-

port the description of the disturbance decoupling

ability of the system. Additionally, the overall tra-

jectory tracking quality is described at the end using

a standard circle test (ballbar-test).

5.1 Tool Stabilization

The ﬁrst simulations describe the system disturbance

response in the frequency domain. In the ﬁrst sim-

ulations the control parameters are conﬁgured for a

critically damped PD control loop with a system fre-

quency Ω = 60Hz. Figure 4(a) shows the tool motion

after application of a 12 Hz, 1 mm sinusoidal signal

at the base. The straight line represents the stimu-

lus in the x-direction, which can be referenced to the

left hand scale. The amplitude of the tool position re-

sponse using a PD control (dotted line) and using a

PD control with additional feed forward disturbance

Figure 4: Response on a 12 Hz, 1 mm sinusoidal trans-

lational base disturbance in x-axis; (a) base position stim-

ulus (straight line, left-hand scale), tool position response

(PD control, dotted line, right-hand scale), tool position re-

sponse multiplied by a factor of two (PD control with distur-

bance feed-forward, dotted line, right-hand scale); (b) Force

needed for feed-forward compensation.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

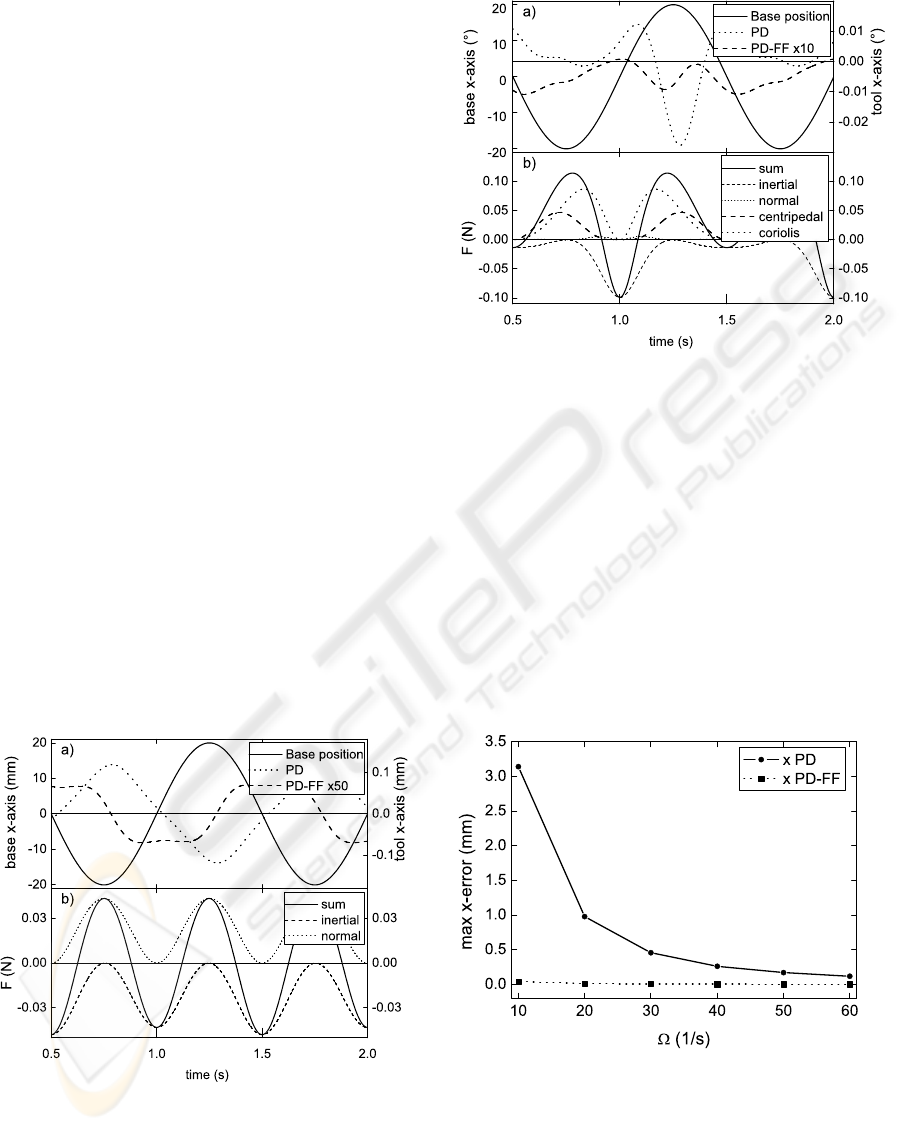
compensation (dashed line) can be extracted from the

right hand scale. For a better readability the later is

multiplied by a factor of two.

As a result the PD controlled tool is damped

against the base disturbance with a transfer factor of

0.3 (-10dB) due to its limited bandwidth. Adding the

feed-forward control the transfer factor decreases to

0.06 (-24dB).

The actuator force needed to cancel the distur-

bances is plotted in Fig. 4(b) for the ﬁrst actuator. The

resulting force F (straight line) is the total of all force

components. The inertial component (dashed line) re-

sults from the tool and the slider acceleration (8) and

the normal component (dotted line) is a consequence

of the strut rotation velocity (6). No Coriolis or cen-

tripedal forces are generated for a translational tool

movement. While the tool-pose reaction seams to be

more or less a sinusoidal function, higher harmonic

distortions are noticeable in the inertial component.

Now, the sinusoidal stimulus is shifted to 1 Hz and

20 mm amplitude (Fig. 5) compared to Fig. 4. Here,

the feed-forward related position response is multi-

plied by a factor of 50. As a result of the lower fre-

quency the PD-loop has an increased damping effect

with a transfer factor of 6 · 10

−3

(-45dB) respectively

6.5· 10

−5

(-84dB) with feed forward control (Fig. 5).

The pose response signal in the large signal case is

not a sinusoidal signal anymore due to the non-linear

coupling between tool and base.

A sinusoidal stimulation of the base orientation

Figure 5: Response on a 1 Hz, 20 mm sinusoidal trans-

lational base disturbance in x-axis; (a) base position stim-

ulus (straight line, left-hand scale), tool position response

(PD control, dotted line, right-hand scale), tool position re-

sponse multiplied by a factor of 50 (PD control with distur-

bance feed-forward, dotted line, right-hand scale); (b) Force

needed for feed-forward compensation.

Figure 6: Response on a 1 Hz, 20

sinusoidal rotational base

disturbance around the x-axis; (a) base orientation stimu-

lus (straight line, left-hand scale), tool orientation response

(PD control, dotted line, right-hand scale), tool orientation

response multiplied by a factor 10 (PD control with distur-

bance feed-forward, dotted line, right-hand scale); (b) Force

needed for feed-forward compensation.

around the x-axis and its response is shown in Fig.

6(a). The forces needed to stabilize the tool are plot-

ted in Fig. 6(b). Here, the Coriolis (large dotted line)

and centripedal (large dashed line) forces are in the

range of the inertia forces. Unlike an intuitive estima-

tion the Coriolis and centripedal components cannot

be neglected in this special robot application.

Figure 7: x- axis response on a 1 Hz, 20 mm sinusoidal

translational base disturbance in dependence on the servo

loop frequency.

The decoupling behaviour from the base motion

strongly depends on the choice of the parameter Ω

and the delay in the feed-back loop, which is at least

one sampling period. This is shown in Fig.7 and Fig.8

DISTURBANCE FEED FORWARD CONTROL OF A HANDHELD PARALLEL ROBOT

Figure 8: x- axis response on a 1 Hz, 20 mm sinusoidal

translational base disturbance in dependence on the sensor

delay.

for a base disturbance of 1 Hz and 1 mm.

The pose error amplitude and phase decrease with

increasing control loop frequency. With disturbance

feed forward control the error is generally smaller,

however the quality strongly depends on the sensor

delay. To estimate the limit time lack that can be al-

lowed the pose error is plotted against the sensing de-

lay. For instance, the delay should not exceed 3 ms,

if a pose accuracy of 0.3 mm is required. (Certainly,

additional error sources must be considered).

5.2 Tracking Control

To assess the possibilities of the disturbance feed for-

ward control the standard circle (ballbar) test was sim-

ulated assuming an additional white Gaussian sen-

sor noise with a translational standard deviation of

accel

= 0.17mm/s

and a rotational standard devia-

tion of σ

rot

= 0.17rad/s for all axes. Figure 9 shows

the reference trajectory, which has to be followed with

a velocity of 0.1 m/s, and the actual trajectories using

a PD control and using a PD control with disturbance

feed forward. The deviation from the reference tra-

jectory is exaggerated by a factor of ﬁve. The mean

pose error are 0.35 mm and 0.10 mm with respectively

without feed forward control. The standard deviations

are 0.051 mm and 0.052 mm. Also for the reference

action the feed forward control diminishes the pose

error remarkably. Because the signal noise from the

base sensors is injected into the inverse kinematics

block as well as into the inverse dynamics block, it in-

ﬂuences the PD control loop once and the PD control

with feed forward control twice. However, the persis-

tent pose noise is not much larger with a feed forward

control compared to the pure PD control approach.

Figure 9: Standard circle test with white Gaussian sensor

noise; σ

accel

= 0.17mm/s

translational standard deviation,

rot

= 0.17rad/s rotational standard deviation, v = 0.1m/s

feed speed.

6 DISCUSSION

The simulations show, that if a complete model of the

parallel robot and adequate sensor signals are avail-

able, a feed forward control can lead to a decoupling

from base disturbances with high damping factors.

For the quality of the decoupling the sensor noise and

the sensor delay are essential. The simulated damp-

ing value of 6.5 · 10

−5

in the 1 Hz case (Fig. 5) must

be interpreted with care, because the quality of the

decoupling is inﬂuenced by numerical errors in this

range. Furthermore, model uncertainties and sensor

errors do not allow such a high precision in real-world

applications. Within the control approach the base

pose, velocity and acceleration must be measured or

observed accurately in the inertia system. This is a

serious problem, because not only sensor latency and

noise must be considered but also misalignment, bias,

drift, etc..

For the simulations an ideal model is assumed

without geometric or parametric errors and without

considering the friction in the actuators and joints.

An enhancement of the dynamic model can be done

with acceptable effort, e.g. the modelling of friction

on the actuator level. However, the quantity of fric-

tion and its inﬂuence on the dynamics depends on

the special mechanical implementation and many pa-

rameters. Therefore a possible model extension must

be considered if the robot is realized. In contrast to

the intuitive impression that for the size, mass and

dynamics of a hand-held robot the Coriolis and cen-

tripedal forces do not play any role, the simulations

show that these force components make a remarkable

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

contribution to the total force in the actuators. Thus,

a simpliﬁcation of the model by neglecting the veloc-

ity related force components is not suitable. Finally,

the simulations show in which range of precision a

feed forward control does improve the decoupling be-

haviour and in which range the feed forward control

can be neglected.

7 CONCLUSION

A model-based approach is presented to control the

tool pose of a handheld robot and to decouple the tool

from base disturbances. An adequate deﬁnition of co-

ordinate frames for the dynamics modelling and the

controller design reduces the effort for the implemen-

tation. The feasibility of a feed-back control on the lo-

cal axis level in combination with a disturbance feed

forward control on the robot level in world coordi-

nates is shown. The local control is able to stabilize

the robot and to avoid huge errors due to model un-

certainties and disturbances. The feed forward control

ensures the free movement of the robot in space, while

measured disturbances can be compensated for. Fur-

thermore, the usage of a non-linear inverse dynamics

model enables the precise disturbance feed-forward

control under different operational conditions. For the

feed-forward control sensor error and delay are cru-

cial.

REFERENCES

Chen, Y. and McInroy, J. E. (2004). Decoupled control of

ﬂexure-jointed hexapods using estimated joint-space

mass-inertia matrix. IEEE Transactions on Control

Systems Technology, 12.

Honegger, M. (1999). Konzept einer Steuerung mit adap-

tiver nichtlinearer Regelung f

ur einen Parallelma-

nipulator. Dissertation, ETH Zurich, Switzerland,

http://www.e-collection.ethbib.ethz.ch.

Honegger, M., Codourey, A., and Burdet, E. (1997). Adap-

tive control of the hexaglide, a 6 dof parallel manipu-

lator. IEEE International Conference on Robotics and

Automation, Albuquerque, USA.

Huynh, P. (2001). Kinematic performance comparison of

linar type parallel mechanisms, application to the de-

sign and control of a hexaslide. 5th International con-

ference on mechatronics technology (ICMT2001), Sin-

gapore.

Koekebakker, S., Teerhuis, P., and v.d. Weiden, A. (1998).

Multiple level control of a hydraulically driven ﬂight

simulator motion system. CESA Conference, Ham-

mammet.

Merlet, J. (2000). Parallel robots. Kluwer Academic Pub-

lisher, Dordrecht, Netherlands.

Pott, P., Wagner, A., K

opﬂe, A., Badreddin, E., M

anner,

R., Weiser, P., Scharf, H.-P., and Schwarz, M. (2004).

A handheld surgical manipulator: Itd - design and ﬁrst

results. CARS 2004 Computer Assisted Radiology and

Surgery, Chicago, USA.

Riebe, S. and Ulbrich, H. (2003). Modelling and online

computation of the dynamics of a parallel kinematic

with six degrees-of-freedom. Archive of Applied Me-

chanics, 72:817–829.

Stewart, D. (1965-1966). A platform with six degrees of

freedom. Proceedings of the Institute of Mechanical

Engineering, 180:371–386.

Takanokura, M. and Sakamoto, K. (2001). Physiological

tremor of the upper limb segments. Eur. J. Appl. Phys-

iol., 85:214–225.

onshoff, H., Grendel, H., and Grotjahn, M. (2002). Mod-

elling and control of a linear direct driven hexapod.

Proceedings of the 3rd Chemnitz Parallel Kinemat-

ics Seminar PKS 2002, 2002 Parallel Kinematic Ma-

chines Int.Conf.

Wagner, A., Pott, P., Schwarz, M., Scharf, H.-P., Weiser,

P., K

opﬂe, A., M

anner, R., and Badreddin, E.

(2004). Control of a handheld robot for orthopedic

surgery. 3rd IFAC Symposium on Mechatronic Sys-

tems, September 6-8, Sydney, Australia, page 499.

Wagner, A., Pott, P., Schwarz, M., Scharf, H.-P., Weiser, P.,

opﬂe, A., M

anner, R., and Badreddin, E. (2006). Ef-

ﬁcient inverse dynamics of a parallel robot with two

movable platforms. 4rd IFAC Symposium on Mecha-

tronic Systems, Heidelberg, Germany.

DISTURBANCE FEED FORWARD CONTROL OF A HANDHELD PARALLEL ROBOT