
MATHEMATICAL MODEL FOR WALKING ROBOT
WITH SHAPE MEMORY ALLOY ANKLE
Anca Petrişor, Nicu George Bîzdoacă
Faculty of Electromechanical Engineering, University of Craiova, Romania
Daniela Roşca, Sonia Degeratu, Adrian Roşca, Raducu Petrisor
Faculty of Electromechanical Engineering, University of Craiova, Romania
Keywords: Robotics, shape memory alloy applications, robotic ankle, walking robot, mathematical model.
Abstract: The paper presents a simultaneous force and length variation mode in shape memory alloy (SMA) robotic
application.
The robotic ankle contains four SMA actuators and a spherical articulation. In order to assure a
high efficient robotic architecture, the mechanical and the control structure have to assure a real-time
response to the work environment changes. The load variations or the difference between the moment of
full contact step and the non contact moment for a waking robot are the standard situations for a SMA
robotic ankle. The paper is divided in five sections. First section makes a short introduction in the physical
description and conventional applications of shape memory alloy materials. Then, are presented the
mathematical model for robotic ankle, the walking robot geometrical structure and the causality ordering of
the active pair of legs, in this case with one free joint. In the last section some experimental results are
presented. These results were obtained by using MATLAB programs, conceived by authors, for design and
simulation of walking robots control algorithms.
1 INTRODUCTION
The shape memory effect was first noted over 50
years ago; it was not until 1962, however, with the
discovery of a nickel titanium shape memory alloy
by Buehler, that serious investigations were
undertaken to understand the mechanism of the
shape memory effect (Bîzdoacă and Pană, 2004),
(Funakubo, 1987), (Graesser and Cozarelli, 1994),
(Schroeder and Boller, 1993).
The shape memory alloys possess the ability to
unde
rgo shape change at low temperature and retain
this deformation until they are heated, at which point
they return to their original shape.
The nickel titanium alloys, used in the present
researc
h, generally refereed to as Nitinol, have
compositions of approximately 50 atomic % Ni/ 50
atomic % Ti, with small additions of copper, iron,
cobalt or chromium. The alloys are four times the
cost of Cu-Zn-Al alloys, but it possesses several
advantages as greater ductility, more recoverable
motion, excellent corrosion resistance, stable
transformation temperatures, high biocompatability
and the ability to be electrically heated for shape
recovery.
Shape memory actuators are considered to be
low power ac
tuators and such as compete with
solenoids, bimetals and to some degree was motors.
It is estimated that shape memory springs can
provide over 100 times the work output of thermal
bimetals.
The use of shape memory alloy can sometimes
sim
plify a mechanism or device, reducing the
overall number of parts, increasing reliability and
therefore reducing associated quality costs.
Because of its high resistivity of 80 – 89 micro
o
hm-cm, nickel titanium can be self heated by
passing an electrical current through it. The basic
rule for electrical actuation is that the temperature of
complete transformation to martensite M
f
, of the
actuator, must be well above the maximum ambient
temperature expected (Delay and Chandrasekaran,
1987).
319
Petri¸sor A., George Bîzdoac
ˇ
a N., Ro¸sca D., Degeratu S., Ro¸sca A. and Petrisor R. (2007).
MATHEMATICAL MODEL FOR WALKING ROBOT WITH SHAPE MEMORY ALLOY ANKLE.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 319-322
DOI: 10.5220/0001626703190322
Copyright
c
SciTePress

2 MATHEMATICAL MODEL OF
SHAPE MEMORY ALLOY
ANKLE
The robotic researches develop up to the present a
various mechanical architecture for ankle structure.
All projects use the human ankle as model.
The problem in developing efficient ankle
structure, concern the dimension and the efficiency
of actuators.
The proposed robot ankle structure contains units
with SMA actuators. The unit has 4 SMA actuators
and a spherical articulation.
Figure 1: The proposed SMA robotic ankle.
Figure 2: Schematically representation of SMA ankle.
Figure 3: Kinematics representation of SMA ankle.
The mathematical model of the ankle is very
simple:
(
)
H,,l
c
12
ankle
α
α=
22c
12 1 1 2c1
12 1 1 2c 1 2
cosα 0sinα lsinα
sin α sin α cos α sin α cos α lsinα cosα
cosα sin α sin α cosα cos α lcosα cos α
000 1
−−
−
2
2
(1)
Analysing the angle dependence versus the SMA
spring variation, a highly nonlinear function results:
()
()
()
22
2l l
c
b
arcsin cos arctg l arctg l
hh
2l
b
⎡⎤
+
⎢⎥
α= +
⎢⎥
⎣⎦
(2)
where l
h
is the length after the heating process; l
c
is
the spring length after cooling and l
b
the base length.
As the real variation is restricted (between 100%
and 92 %), the linearization can occur because of
linear behaviour for the specified evolution
(Bîzdoacă and Pană, 2003).
3 WALKING ROBOT
GEOMETRICAL STRUCTURE
It is considered the walking robot structure as
depicted in Fig.4, having three normal legs
and a head equivalent to another leg, L
ijp
L,L,L
0,
containing the robot centre of gravity, G, placed in
its foot. The robot body RB is characterized by two
position vectors O
0
, O
1
and the leg joining points
denoted R
i
, R
j
, R
p
. The joining point of the head, L
0
,
is the central point O
0
, R
0
= O
0
, so the robot body RB
is univocally characterized by the set,
01ijp0
RB {O , O , , , , }
=
λλλ λ
(3)
where
0
0
λ
= .
u
1,0
G
0
=G
R
p
Figure 4: Geometrical structure of the robot.
u
1,j
u
1,i
u
2,i
G
i
O
1
O
0
R
j
u
2,j
u
1,p
G
p
u
2,p
u
2,0
R
0
R
i
G
j
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
320
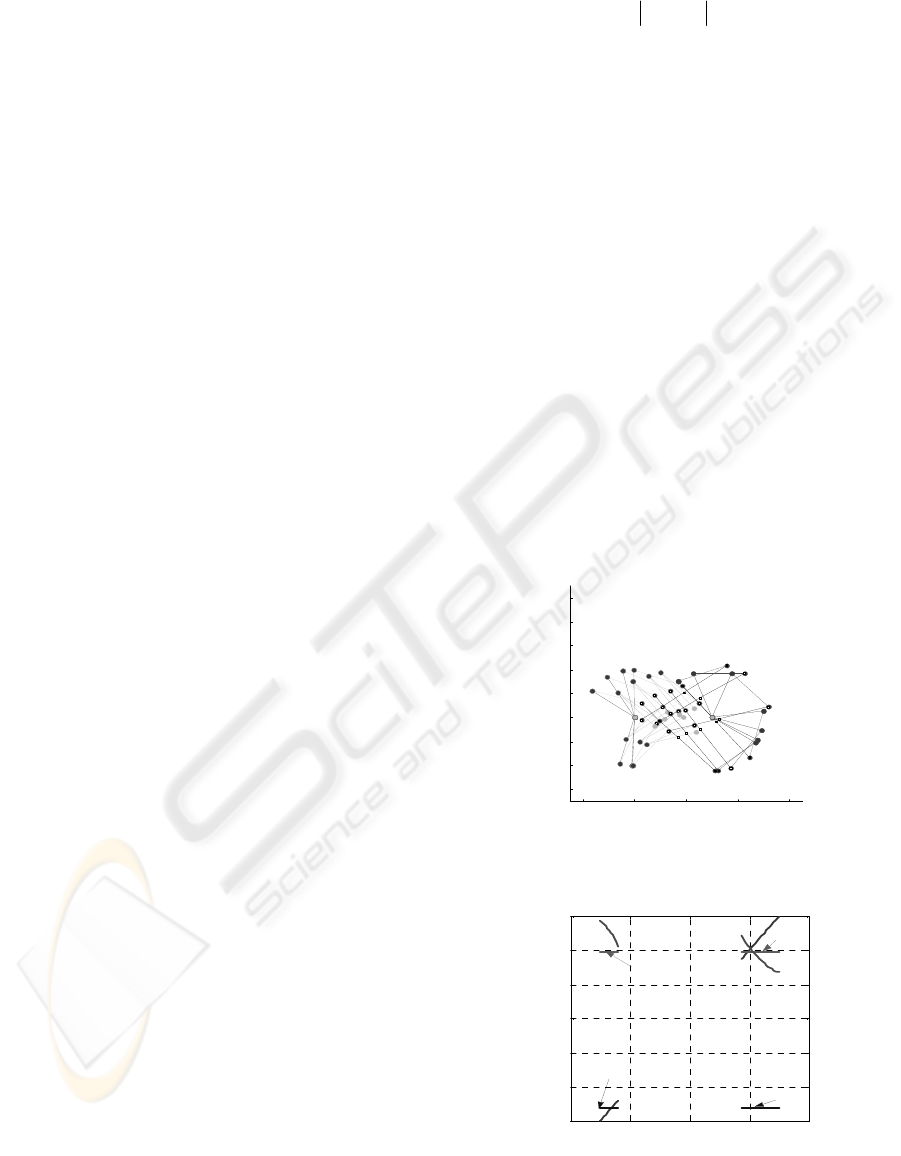
The robot position in the vertical plane is defined
by the pair of the position vectors O
0
, O
1
where
, or by the vector O
10
|O O | 1−=
0
and the scalar θ,
the angular direction of the robot body.
Each of the four robot legs is
characterized by a so-called Existence Relation
ER(L) depending on specific variables as it is
presented in (Petrişor, 2005), (Petrişor, Marin,
Bîzdoacă and Cazacu, 2006).
ijp0
L,L,L ,L
The mathematical model of this object is a
Variable Causality Dynamic Systems VCDS and it
is analiyzed from this point of view.
A pair of legs {L
i
, L
j
} constitutes the so called
Active Pair of Legs (APL) if the robot body position
is the same irrespective of the feet position of all the
other legs different of
i
L
and
j
L
. A label is assigned
to each possible APL. The APL label is expressed
by a variable called Index of Activity (IA), which
can take N
q
a
values, numbers or strings of characters.
All the other legs that at a time instant do not belong
to APL are called Passive Legs (PL). The leg in
APL, having a free joining point is called slave leg,
the opposite of the motor leg whose both joining
points are external controlled.
4 CAUSALITY ORDERING OF AN
ACTIVE PAIR OF LEGS WITH
ONE FREE JOINT
In this structure, only one angle is free so three joints
are external controlled (EC).It is denoted this by
q'ij'=
,
p
c [motor12, motor01, c ]=
(4)
This causality ordering is corresponded to the
state having the leg L
i
as a motor leg which controls
two degree of freedom and the leg L
j
, a slave leg,
which can control only one scalar component , so
the angle is free and the angle is EC.
2, j
u
1, j
u
In this structure is obtained from the
following relations:
2, j
u
2, j j
2j
2, j
(t)
2, j j
2j
ˆ
if u (t ) 0 s up
u
ˆ
if u (t ) 0 s down
⎧
ψ−ε>⇔
⎪
=
⎨
−ψ −ε ≤ ⇔ =
⎪
⎩
=
(
5)
2j 2j 2j 2j
2, j
(t)
2j 2j 2j 2j
dacă 0
u
dacă 0
−ϕ + ψ −ϕ + ψ ≤
⎧
⎪
=
⎨
−ϕ +ψ −π −ϕ +ψ >
⎪
⎩
(6)
2j 2j 2j 2j
2, j
(t)
2j 2j 2j 2j
dacă 0
u
dacă 0
−ϕ + ψ + π −ϕ + ψ ≤
⎧
⎪
=
⎨
−ϕ + ψ −ϕ + ψ >
⎪
⎩
(7)
Therefore, in this causality structure the
kinematics restriction
ji
ij
RR r
−
=
is accomplished
by changing the value of
u at giving by the
equation (5), (6), (7).
2, j 2, j
u
5 EXPERIMENTAL RESULTS
The causal ordering c=[motor12, motor 01, c
p
] is
implemented together with other causal orderings, in
the RoPa platform for design and simulation of
walking robots control algorithms. The RoPa
platform is a complex of Matlab programs to
analyze and design walking robots, evolving in
uncertain environments according to a new control
approach called Stable State Transition Approach
(SSTA), also conceived by the authors.
The causal ordering developed in this paper is
activated by selecting the causal variable
cz=[12 1 0]. The RoPa platform allows animation,
recording of the evolutions and playback them.
In the following there are presented some
experimental results of walking robot behaviour
considering this causal ordering.
4
3
2
Figure 5: The robot kinematics evolution.
Figure 6: Controlled angles with respect to the input angle.
-2 0 2 4 6
-3
-2
-1
0
1
5
RoPa1Ex2S1V1q132cz1210
x
y [m]
[
m
]
3
-4 -2 0 2 4
-3
-2
-1
0
1
←
u
2,3
u
1,3
2
u
1,1
u
1,1
u
2,1
u
1,3
u
2,3
G
1
= 0
G
3
= 3
←
u
1,1
u
2,1
u
1,3
←
u
2,3
u
2,1
MATHEMATICAL MODEL FOR WALKING ROBOT WITH SHAPE MEMORY ALLOY ANKLE
321
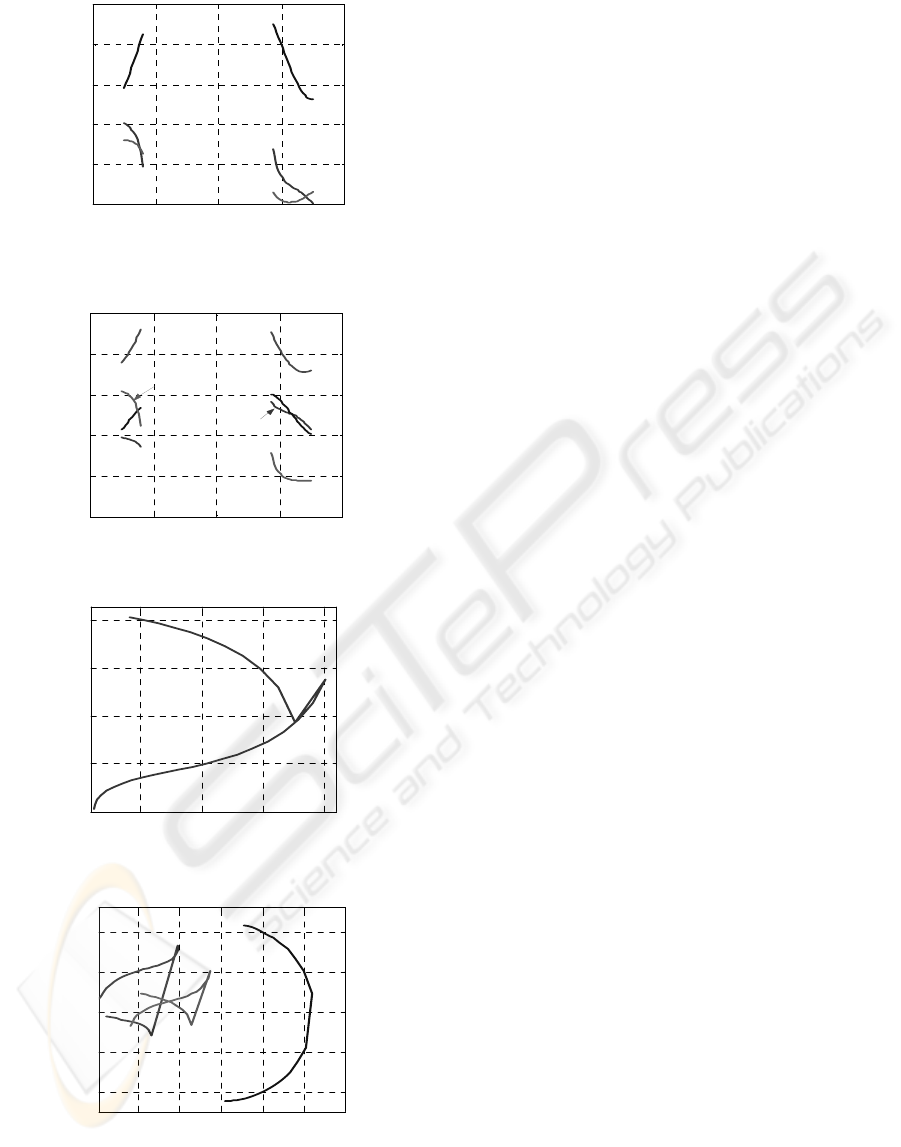
Figure 7: Robot body position with respect to the input
angle.
Figure 8: Joints positions with respect to the input angle.
Figure 9: Reference point O
0
locus in evolution scene.
Figure 10: Joints points' locus in evolution scene.
6 CONCLUSIONS
-4 -2 0 2 4
-1
0
1
2
3
4
u
1,1
Im(O
0
) Re(O
0
)
θ
G
1
= 0
G
3
= 3
←
Im (O
0
)
←
Re(O
0
)
←θ
←
Re(O
0
)
←
Im (O
0
)
←θ
Shape memory alloy ankle add to the walking robot
architecture additional control possibility for
adapting the structure to various environment.
The causal ordering developed in the paper is
useful when it must control the shoulder position R
i
irrespective of the other variables. It can be
controlled by the angle u
1,j
, the shoulder angle of the
second active leg L
j
.
The approach of the kinematics structure by
complex number representation of the variables
allowed to solve the equations system that describe
the position of the variables that are involved,
between witch there are kinematics correlations. In
this way, it is obtained an explicit representation of
the input-output dependence, in this causality
structure.
-4 -2 0 2 4
-4
-2
0
2
4
6
u
1,1
Im(R
1
) Re(R
1
) Im(R
3
) Re(R
3
)
G
1
= 0
G
3
= 3
←
Im (R
1
)
←
Re(R
1
)
Im (R
3
)
←
Re(R
3
)
←
Re(R
3
)
Im (R
1
)
←
Re(R
1
)
←
Im (R
3
)
As it can be seen from the above experimental
results, this causal ordering is perfectly integrated in
the RoPa structure proving the correctness of the
theoretical results.
The mathematical model developed in the
paper becomes an element of the VCDS walking
robot model. The simulations used MATLAB
environment show the robustness of the
mathematical model.
2 2.5 3 3.5
-1
-0.5
0
0.5
1
Real(O
0
)
Imag(O
0
)
G
1
= 0
G
3
= 3
←
Imag(O
0
)
REFERENCES
Bîzdoacă, N., Pană D., 2003. Shape memory alloy tendon
driven finger. In Proceedings of the 14th international
conference on control systems and computer science,
CSCS15, Bucharest, Romania, May 25-27.
Bîzdoacă, N., Pană D., 2004. Shape Memory Alloy Based
Robotic Ankle. In Proceedings of the 5th International
Carpathian Control Conference, ICCC 2004, Vol. I.
Delay, L., Chandrasekaran M., 1987. Les Editions
Physique. Les Ulis.
Funakubo, H., 1987. Shape Memory Alloys. Gordon and
Breach Science Publishers.
1 2 3 4 5
-2
-1
0
1
2
Re(R
1
) Re(R
3
) Re(R
2
)
Im(R
1
) Im(R
3
) Im(R
2
)
G
1
= 0
G
3
= 3
←
Im (R
1
)
←
Im (R
3
)
←
Im (R
2
)
Graesser, E.J., Cozarelli F.A., 1994. Journal of Intelligent
Material Systems and Structures, no.5.
Petrişor, A., 2005. Walking mouvement with controlled
style of the passive leg. In Proceedings of the 15th
international conference on control systems and
computer science, CSCS15, Bucharest, Romania, May
25-27, 2005, pag.483-487.
Petrişor, A., Marin, C., Bîzdoacă, N., Cazacu, D. 2006.
Variable Causality Dynamic System Approach for
Robot Control. WSEAS Transactions on Systems and
Control Journal, Issue 1, Volume 1, Nov., pp.26-30
Schroeder, B., Boller, Ch., 1998. Comparative Assessment
of Models for Describing the Constitutive Behaviour
of Shape Memory Alloy, Smart Materials and
Structures.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
322
