ACTIVE 3D RECOGNITION SYSTEM BASED ON FOURIER

DESCRIPTORS

E. González, V. Feliú, A. Adán* and Luis Sánchez**

H.T.S. of Industrial Engineering, University of Castilla La Mancha, Ave. Camilo José Cela s/n

Ciudad Real, 13071, Spain

*Higher School of Informatics,Universit

y of Castilla La Mancha, Ronda de Calatrava 5

Ciudad Real, 13071, Spain

**U.E of Technical Industria

l Engineering,University of Castilla La Mancha, Ave Carlos III, s/ n

Toledo, 45071, Spain

Keywords: Active recognition system, nex

t best view, silhouette shape, Fourier descriptors.

Abstract: This paper presents a new 3D object recognition/pose strateg

y based on reduced sets of Fourier descriptors

on silhouettes. The method consists of two parts. First, an off-line process calculates and stores a clustered

Fourier descriptors database corresponding to the silhouettes of the synthetic model of the object viewed

from multiple viewpoints. Next, an on-line process solves the recognition/pose problem for an object that is

sensed by a real camera placed at the end of a robotic arm. The method avoids ambiguity problems (object

symmetries or similar projections belonging to different objects) and erroneous results by taking additional

views which are selected through an original next best view (NBV) algorithm. The method provides, in very

reduced computation time, the object identification and pose of the object. A validation test of this method

has been carried out in our lab yielding excellent results.

1 INTRODUCTION

Most computer vision systems used in robotics

environments perform 3D object recognition tasks

using a single view of the scene (Bustos et al.,

2005). Commonly, a set of features is extracted and

matched with features belonging to an object

database. This is why so many researchers focus

their recognition strategy on finding features which

are capable of discriminating objects efficiently

(Helmer and Lowe, 2004). However, these

approaches may fail in many circumstances due to

the fact that a single 2D image may be insufficient.

For instance, this happens when there are objects

that are very similar from certain viewpoints in the

database (ambiguous objects); a difficulty that is

compounded when we have large object databases

(Deinzer et al., 2003).

A well known strategy that solves the ambiguity

oblem is based on using multiple views of the

object. Active recognition systems provide the

framework to efficiently collect views until the

sufficient level of information for developing the

identification and posing estimation tasks is obtained

(Niku, 2001).

Previous works on active recognition differ in

the way they

represent objects, the way they

combine information and the way of they plan the

next observation (Roy et al., 2004). These systems

use 3D representation schemes based on the object

geometric model or on the object appearance.

Although X recognition based on geometric models

might be potentially more effective and allow for the

identification of objects in any position, they raise

important problems of practical aplicability.

Moreover, the methods based on X appearance are

currently the most successful approaches for dealing

with 3D recognition of arbitrary objects.

Many strategies for solving the 3D object

recogn

ition problem using multiple views have been

proposed: an aspect graph is used in Hutchinson and

Kak (1992) to represent the objects. This criterion

handles a set of current hypotheses about the object

identity and position. It characterizes the recognition

ambiguity by an entropy measure (Dempster-Shafer

theory) and evaluates the next best sensing operation

by minimizing this ambiguity. Borotsching et al.

318

González E., Feliú V., Adán A. and Sánchez L. (2007).

ACTIVE 3D RECOGNITION SYSTEM BASED ON FOURIER DESCRIPTORS.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 318-325

DOI: 10.5220/0001627003180325

 SciTePress

(1999) represent the objects by some appearance-

based information, namely the parametric

eigenspace. This representation is augmented by

adding some probability distributions. These

probability distributions are then used to provide a

gauge for performing the view planning. Sipe and

Casasent (2002) use a probabilistic extension of the

feature space trajectory (FST) in a global eigenspace

to represent 3D views of an object. View planning is

accomplished by determining - for each pair of

objects – the most discriminating view point in an

off-line training stage. Their approach assumes that

the cost of making a mistake is higher than the cost

of moving the sensor.

In general, most of these approaches solve the

3D object recognition problem using stochastic or

probabilistic models and, consequently, they require

a large dataset for training (Deinzer et al., 2006).

Here we present a different way to focus on the

problem.

The key to our active recognition system consists

of using a reduced set of Fourier descriptors to

connect and develop the recognition phases: object

representation, classification, identification, pose

estimation and next best view planning.

We focus the object representation on silhouettes

because: they can be robustly extracted from

images, they are insensitive to surface feature

variations - such as color and texture - and, finally,

they easily encode the shape information (Pope et

al. 2005). The most popular methods for 2D object

recognition from silhouettes are based on invariant

moments or Fourier descriptors. Invariant moments

exhibit the drawback that two completely different

silhouettes may have the same low order invariant

moments, which may lead to ambiguities in the

recognition process. Fourier descriptors yield much

more information about the silhouette, and only

similar silhouettes exhibit similar Fourier

descriptors. Since we consider the objects to be non-

occluded and the background to be uncluttered, we

use a representation scheme in which the silhouettes

from different viewpoints are represented by their

Fourier descriptors.

This paper is organized as follows. Section 2

presents an overview of the method. Section 3

describes our object identification/pose estimation

approach. Section 4 details the next best view

method. Section 5 shows the performance of our

method by carrying out experiments on a real

platform, and some conclusions are stated in Section

2 OVERVIEW OF THE METHOD

In this method the scene silhouette (silhouette of the

3D object to be recognized) is recognized among a

set of silhouettes (in our case, 80 or 320 per object)

of a group of objects through an algorithm based on

Fourier descriptors. Therefore, X recognition of the

silhouette of the scene involves both object

identification and pose. The method consists of off-

line and on-line parts.

The off-line process consists of building a

structured database of silhouettes belonging to a

generic set of objects. Firstly, a high precision three-

dimensional model of each object is obtained by

means of a laser scanner sensor. Next, this model is

viewed from a set of homogeneous viewpoints

obtaining the corresponding set of 2D silhouettes.

The viewpoints correspond to the vertexes of a

tessellated sphere with origin in the centre of mass

of the object. Figure 1 shows an object model inside

the tessellated sphere, the projected image of the

model and its silhouette from a specific viewpoint.

Figure 1: a) Object model put into the tessellated sphere b)

View of the object model from a specific viewpoint, c)

Depth image d) 2D silhouette.

The database is structured in clusters using only

three Fourier descriptors. To build the clustering we

used a k-means algorithm (Netanyahu et al., 2002).

This strategy allows us to split the silhouette search

space in zones where the silhouettes are roughly

similar. Consequently, the cost of the recognition

process is dramatically reduced. Figure 2 a) shows

the most important Fourier descriptors modules for a

couple of silhouettes. In our case, we have taken the

second, third and next to the last values. Figure 2 b)

presents the reconstructed silhouette with the three

Fourier descriptors superimposed on the original

one. Note that by selecting the most meaningful

Fourier components it is possible to work with

approximate shapes. Figure 3 shows a spatial

ACTIVE 3D RECOGNITION SYSTEM BASED ON FOURIER DESCRIPTORS

319

representation of the clusters that have been

extracted in our database.

The on-line process is designed to solve the

recognition/pose problem of an object that is viewed

by a camera in a real environment. The essential

steps are: Fourier descriptor calculation,

classification (discrimination) process,

identification/pose calculation and next view

algorithm. Next, a brief explanation of these steps is

provided.

Figure 2: a) Fourier descriptors modules b) silhouette (red)

and silhouette recovered with three Fourier descriptors

(blue).

To calculate the Fourier descriptors a suitable

image preprocessing is carried out on the original

image. Specifically this process consists of filtering,

thresholding and contour extraction. Next the points

of the contour are taken as a sequence of complex

numbers and the Fourier descriptors are finally

computed.

The discrimination phase classifies the silhouette

of the scene into a single or a set of clusters. The

selected clusters constitute the work sub-space in the

pose phase. Formally,

Let a database of N objects, C

...O ,O,O

N21

the

kth cluster, k ∈ [1..K], the n-th silhouette of

the object m, the k-th cluster prototype, D the

Euclidean distance, the k-th cluster radius where

and z the silhouette of the

scene to be matched. The subspace will be

formed by the clusters, which verify one or both of

the following conditions:

) S,D(pmax R

kkk

sub

Criterion 1: If

subkkk

SCthenRzpD ∈<),(

Criterion 2:

[1..K] i ,S C then |minD - D·|

subiki

∈∈

The criterion 1 is satisfied for cases where z is

inside a cluster whereas criterion 2 corresponds to

cases where the silhouette z is inside an area with

very high cluster density or where the scene

silhouette falls outside the clusters. Thus, the

discrimination process sets a work subspace

with a reduced database of silhouettes.

sub

The identification phase, which is carried out

in , yields, in general, a reduced set of candidate

silhouettes. The reason for taking only a few

candidates is as follows. Matching and alignment

techniques based on contour representations are

usually effective in 2D environments. Nevertheless,

in 3D environments these techniques have serious

limitations. The main problems with the contour

based techniques occur due to the fact that the

information on the silhouettes may be insufficient

and ambiguous. Thus, similar silhouettes might

correspond to different objects from different

viewpoints. Consequently, a representation based on

the object contour may be ambiguous, especially

when occlusion circumstances occur.

sub

In essence, the identification phase compares the

silhouette from the scene with the silhouettes in the

subspace by means a quadratic error

minimization applied on the modulus of the Fourier

descriptors. If the identification/pose process

proposes more than one candidate silhouette, then

the solution is ambiguous and it is necessary to

apply the Next Best View planning method (NBV).

Figure 4 shows a scheme with the main process.

sub

Figure 3: Spatial representation of the silhouette clusters.

In most cases, the recognition and pose estimation

phase is finished after several views of the object are

taken and only one candidate is found. In this

process, the position of the next view is calculated

through an algorithm based on the set of candidate

silhouettes obtained in the previous view. This will

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

320

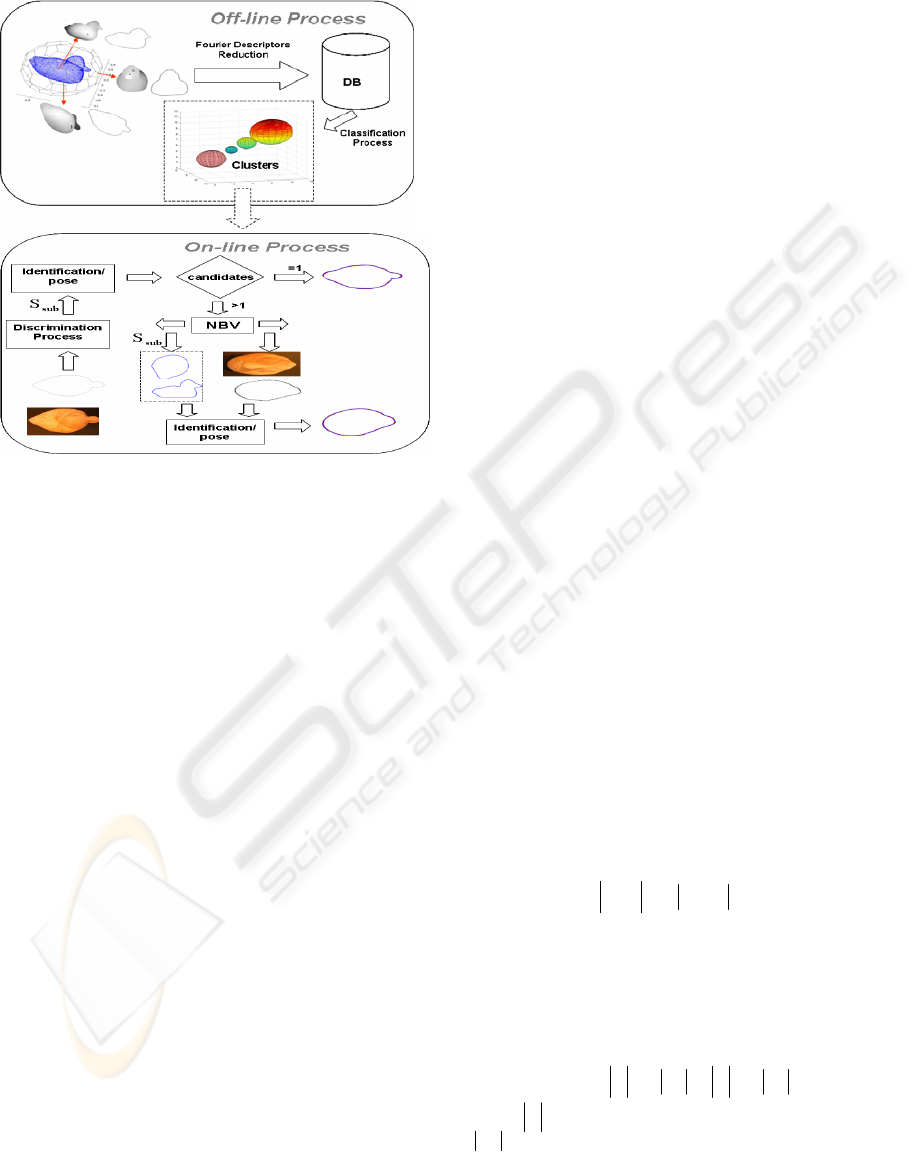
be explained in Section IV. Figure 4 shows a scheme

of the main process.

Figure 4: Diagram of the active recognition system.

3 OBJECT RECOGNITION AND

POSE ESTIMATION

PROCEDURE

Fourier descriptors can be used to represent closed

lines (silhouettes). They can be made invariant to

translations and rotations, and allow easy filtering of

image noise (

Deinzer et al., 2003). Assume a contour

l(n) composed of N points on the XY plane:

[]

1..0,)(),()( −== Nnnynxnl

(1)

where the origin of index n is an arbitrary point of

the curve, and n and n+1 are consecutive points

according to a given direction (for example

clockwise direction) over the silhouette. Assume

also that points over the curve have been regularized

in the sense that two consecutive points are always

at the same Euclidean distance. Let us define the

complex sequence and its discrete Fourier

transforms Z(k)=F(z(n))as

)()()( njynxnz +=

∑

−

−=

)/2exp()()(

NknjnzkZ

10 −≤≤ Nk

(2)

(3)

Assume also a data base of R silhouettes

with

),(ns

10 −≤≤

Nn R

≤≤1 , whose respective

discrete Fourier transforms are S

(k).

A critical aspect of our method is its computation

time. Then the FFT algorithm is used to obtain the

Fourier descriptors. Then N must be power of 2 and

both the scene silhouette and the silhouettes of the

data base must be regularized to a number of N = 2

speed because we want to recognize objects in real

asic problem to be solved in our method is

N’

points.

The b

match the scene silhouette z(n) to some silhouette

(n) of the data base, under the assumptions that

z(n) may be scaled (

), translated (

jcc + ) and

rotated (

) with respect to the ching

silhouette of the data base, and that the reference

point on z(n) (n = 0) may be different from the

reference point of that data base silhouette (we

denote that displacement

best mat

). The next section deals

with selecting the silhoue es and obtaining X c,

3.1 Close Silhouettes Selection

Suppose that z is the silhouette of an object captured

by the camera and that it corresponds to the

silhouette s

(n) that belongs to the silhouette

database. In general, z is matched to s

(n) after

displacement, rotation, scaling and centre translation

parameters are found. In general for

),(ns

in the

space domain:

Dnz cjns

)exp()),(()(

(4)

where displaces

))(( nsD

units the in

the e u

orig of

sequenc . Taking Fo rier transform:

cNkSNkjkZ

)(ns

)()/2xp(exp)( e)(

(5)

• Translation: Since all silhouettes have

the

coordinate origin at their centre of mass

0)0(

S and from expression (5) ,

N/Zc )0(

• Close silhouettes identification.: Defining

cNkZkZ −= )()(



, the modulus of expression

(5) holds:

)()( kSkZ



(6)

The matching procedure minimizes the mean

uared error between the Fourier descriptors of the

scene silhouette and the silhouettes of the database.

Given a pair of silhouettes

))(),(( nsnz

, the

similarity index

J is defined as

)()()(

ZSJ

λλ

−−=

rrr



(7)

wher

NZZZ |)1(||,)0((| −=

∧∧

…



S = NS |)1(||)0((| −…

,| . |=absolute value.

Minimizing

)(

J with re

spect to the scaling

ctor

, we obtain:

ACTIVE 3D RECOGNITION SYSTEM BASED ON FOURIER DESCRIPTORS

321





−= ZZJ





)(



(8)

After calculating for all silhouettes of the data

ba ho

other viewpoin

3.2 Pose Calculation

the set of indexes

e silhouettes. In



se we select the sil uettes which verify UJ

≤



U being a specific threshold. In this case, we

of many ambiguous silhouettes

{

cfc2c1

S . . . ,S,S } and it is necessary to select

an t to solve the ambiguity problem

(NBV section).

have a

set

Let us denote ),,,(

21 m

rrrL …=

of the candidat order to select the

best candidate among

candidates, a more accurate

procedure is carried o t. This procedure uses the

complete complex Fourier descriptors (not only the

modules as in the previous process). As a result of

this process, a new similarity index



f is obtained

and the pose parameters

are ca lated.

The cost function to be ized is (see (4)):

lcu

minim

(9)

where

NZ −…

))(

())(

(),,(

δδδθλ

PqZPqZf

−−=

∗

,))1(

,),0(

(

ZZ =

rrrr

NNj

NsNjssP

))/)1(2exp(

)1(,,),/2exp()1(),0(()(

−

−=

πδ

…

∗ denotes conjugate,

∗

denotes transpose

njugate, and

is restricted now to set

Let us denote

qj =)exp(

, opt iim zing (9)

res

pect to the complex number

q :

ZZf

∗

)(

(10)

∗

−==

)(

)(,)(

δδ



notice that ).

to account that

≤≤ N

(

SSPP ⋅=

∗∗

)()(

δδ

Taking in

1−0 is i

nteger,

e right expression of (10) is calculated for all

possible values of

and )(

min



ff = is

determined.

Then



f is the similarity index of the silhouette

in t fine matching process,



is the

corresponding displacement and is obtained

from ¿the? left equation of (10) particularized to .

Rotation and scaling are estimated from :





rrrr

qq ∠==

ϕλ

;

(11)

4 NEXT BEST VIEW PLANNING

The goal of this phase is to provide a solution to the

ambiguity problem by taking a set of optimal

viewpoints. When an ambiguous case occurs, we

move the camera to another viewpoint from which

the silhouettes of the candidate objects are

theoretically very dissimilar.

As said before, in our scheme representation we

associate each silhouette stored in the database with

a viewpoint of the tessellated sphere. Then, the first

step in the NBV consists of aligning the candidate

spheres (corresponding to the viewpoints in our

models) with the scene sphere.

Let T

(S) be the tessellated sphere, N'

the

camera position and N

the viewpoint that

corresponds to the candidate silhouette . To align

the two spheres a rotation must be applied to make

and N

coincident (Adán et al., 2000).

Formally:

Let

zyx

ONON

uuu

),,(

→



be the normal

vector to the plane defined by and , O

being the center of

→

ON'

→

. Let

be the angle between the

last two vectors. Then, a rotation

around the u axis

can first be applied to

(S). This spatial

transformation is defined by the following rotation

matrix R

(

⎟

⎠

⎞

⎜

⎝

⎛

+−+−−−

−−+−+−

+−−−+−

θθθθθθ

ccuusucuusucuu

sucuuccuusucuu

sucuusucuuccuu

zzxzyyzx

xzyyyzyx

yzxzyxxx

)1(.)1(.)1(

.)1()1(.)1(

.)1(.)1()1(

)(

(12)

where

=cos

and s

=sin

A second rotation

around the axis

zyx

vvv

),,(

→



is required to achieve

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

322

the best fitting of

(S) to T

(S') (see Figure 5). The

swing angle

is determined by (14). This last set of

points can be obtained by applying a rotation matrix

Rv(

ϕ) that depends on a single parameter ϕ and can

be formally expressed as

⎟

⎠

⎞

⎜

⎝

⎛

+−+−−−

−−+−+−

+−−−+−

ϕϕϕϕϕϕ

ccvvsvcvvsvcvv

svcvvccvvsvcvv

svcvvsvcvvccvv

zzxzyyzx

xzyyyzyx

yzxzyxxx

)1(.)1(.)1(

.)1()1(.)1(

.)1(.)1()1(

)(

(13)

(

)=R

(

)·R

(

)

(14)

Finally the alignment of the spheres is:

)(T),(R)(T

SS ⋅=

θϕ

(15)

In the next step the Fourier energy is calculated

for each viewpoint.

Defining , where ,

icp

OS ∈

jcq

OS ∈

∈

]S...S,S[

cf2C1c

, where is the number of

candidate silhouettes, and

vp is a viewpoint from

(S). The energy is computed for all couples of

silhouettes as follows:

fjfiji

kZkZ

OjOi

≤≤≠∀

−=

∑

−

,|)()(|

(16)

)min(

OjOi

EE =

(17)

The NBV ν is defined as the viewpoint that

verifies:

pEE

∀= )max(

(18)

Figure 5: Alignment process between candidate spheres

and the scene sphere.

Finally, the camera is moved to the best viewpoint

and a new image of the scene is captured and

matched with the model silhouette correspondents to

the best viewpoint using (9) and (11) equations.

Figure 6: Superimposed models after the alignment

process and energy values plotted on the nodes.

5 EXPERIMENTATION

A validation test of this method has been carried out

in our lab. The experimental setup is composed of a

Stäubli RX 90 Robot with a micro camera Jai-

CVM1000 at its end. This system controls the

position and vision direction on the camera, the

object always being centered in the scene. Figure 7

shows the experimental setup.

In the off-line process, the synthesized models

(with 80000 polygons/object) are built through a VI-

910 Konica Minolta 3D Laser scanner. At the same

time the silhouette database with their respective

Fourier descriptors are obtained and stored.

Currently we have used databases of 80 and 320

silhouettes/model.

In order to reduce redundant information and to

optimize the recognition/pose time, a Fourier

descriptors reduction has been carried out on the

silhouette models. Figure 2.a shows Fourier

descriptors modulus for an example. As X can be

seen, the first and the last descriptors are the most

meaningful. The reduction procedure consists of

considering the intervals [1,X(k)], [X(N-k),X(N)],

k=1,…N, until the error/pixel between the original

and reduced silhouettes is less than a threshold

a) b)

Figure 7: a) Experimental Setup. b) Examples of synthetic

models.

ACTIVE 3D RECOGNITION SYSTEM BASED ON FOURIER DESCRIPTORS

323

The experimentation has been carried out with

19 objects that have been previously modelled with

80 and 320 views, considering descriptor reductions

=0.05 and

=0.5.

In the clustering process we have used 50

clusters. During this phase we use images with

resolution 640x480. Each silhouette in the database

was stored with a resolution of 512 points and the

database size was 12 MB (80 views) and 42 MB

(320 views).

Table 1.

# sil.

0.05 2.652 1.640 2.475 2.382

0.5

2.047 1.653 1.863 2.473

0.05 4.901 1.089 4.739 2.107

320

0.5 3.336 1.339 3.096 2.261

The active 3D recognition system worked in all

tests achieving 100% X effectiveness. Table 1

shows the results obtained during the recognition

process without (A) and with (B) discrimination

phase. The results are compared taking into account:

the number of silhouettes of the model, threshold for

Fourier descriptors reduction (

), mean square

error between the silhouette of the scene and the

estimated silhouette (

ρ). Variable t is the

computation time (seconds) on a Pentium III 800

Hhz processor.

Table II shows in detail the main process rates

using a database with 80 silhouettes/model and a

reduction factor

=0.5.

From Tables 1 and 2 the following comments can

be made.

• In the whole process, most of the time is

devoted to extracting the object’s silhouette

(88,6% and 94,7%). Note that, this stage

includes several image preprocessing tasks

like filtering, thresholdin, etc. In part, such

a high percentage is also due to the fact that

we have used a reduced object database in

our experimentation. For large databases

(>100-500 objects) this percentage will

decrease at the same time that the

percentage corresponding to the candidates

selection stage will increase.

• Using 320 silhouettes per model increases

in a double the execution times with respect

the use of 80 silhouettes per model but the

decreases by 0,3 percent.

Table 2.

Algorithm

time (%)

Silhouette extraction

88.6

Identification

7.9

Pose estimation

1.4

Without

clustering

NBV

2.1

Silhouette extraction

94.7

Discrimination

0.8

Identification

2.2

Pose estimation

0.6

With

clustering

NBV

1.7

Figure 8: Comparison of discrimination between a random

method and our proposed method.

Two experiments were carried out: one running

our active recognition system which uses a random

selection of the next view, and another computing

the next best view from our D-Sphere structure. In

Figure 8 we can see the number of candidates in

each sensor position for a real case. The test average

reported that our method considerably reduced the

number of sensor movements: about 62%. The time

needed to calculate the next observation position is

very short: approximately 1.7% of all the time

needed to carry out a complete step of the

recognition process. Calculations were performed on

a Pentium III 800 Hhz processor. The active 3D

recognition system worked in all tests achieving

100% X effectiveness. Figure 9 illustrates a case of

ambiguity between two objects and how the system

solves the problem. Our NBV method shows much

higher discriminative capability than the random

method. Thus, the proposed strategy significantly

improves the recognition efficiency.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

324

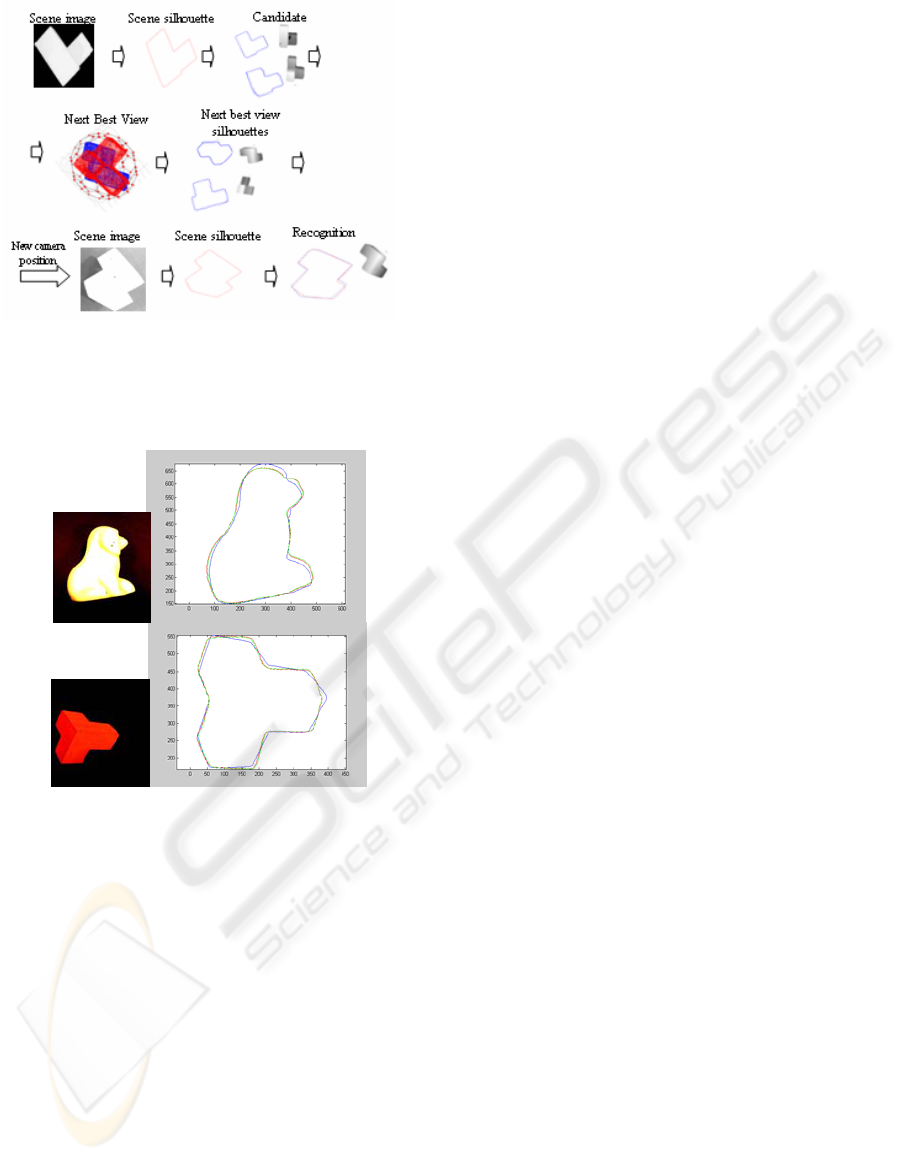
Figure 9: Solving an ambiguous case.

Figure 10 presents some matching and pose

estimation results using the proposed algorithm.

Figure 10: Some examples of 3D recognition without

ambiguity.

6 CONCLUSION

This paper has presented a new active recognition

system. The system turns a 3D object recognition

problem into a multiple silhouette recognition

problem where images of the same object from

multiple viewpoints are considered. Fourier

descriptors properties have been used to carry out

the clustering, matching and pose processes.

Our method implies the use of databases with a

very large number of stored silhouettes, but an

efficient version of the matching process with

Fourier descriptors make it possible to solve the

object recognition and pose estimation problems in a

greatly reduced computation time.

On the other hand, the next best view (NBV)

method efficiently solves the frequent ambiguity

problem in recognition systems. This method is very

robust and fast, and is able to discriminate among

very close silhouettes.

REFERENCES

Adán, A., Cerrada, C., Feliu, V., 2000. Modeling Wave

Set: Definition and Application of a New Topological

Organization For 3D Object Modeling. Computer

Vision and Image Understanding 79, pp 281-307.

Bustos, B., Kein, D.A., Saupe, D., Schreck, T., Vranic, D.,

2005. Feature-based Similarity Search in 3D Object

Databases. ACM Computing Surveys (CSUR)

37(4):345-387, Association For Computing

Machinery.

Borotschnig, H. Paletta, L., Pranti, M. and Pinz, A. H.

1999. A comparison of probabilistic, possibilistic and

evidence theoretic fusion schemes for active object

recognition. Computing, 62:293–319.

Deinzer, F., Denzler, J. and Niemann, H., 2003. Viewpoint

Selection. Planning Optimal Sequences of Views for

Object Recognition. In Computer Analysis of Images

and Patterns, pages 65-73, Groningen, Netherlands,

Springer.

Deinzer, F., Denzler, J., Derichs, C., Niemann, H., 2006:

Integrated Viewpoint Fusion and Viewpoint Selection

for Optimal Object Recognition. In: Chanteler, M.J. ;

Trucco, E. ; Fisher, R.B. (Eds.) : British Machine

Vision Conference

Helmer S. and Lowe D. G, 2004. Object Class

Recognition with Many Local Features. In Workshop

on Generative Model Based Vision 2004 (GMBV),

July.

Hutchinson S.A. and Kak. A.C., 1992. Multisensor

Strategies Using Dempster-Shafer Belief

Accumulation. In M.A. Abidi and R.C. Gonzalez,

editors, Data Fusion in Robotics and Machine

Intelligence, chapter 4, pages 165–209. Academic

Press,.

Netanyahu, N. S., Piatko, C., Silverman, R., Kanungo, T.,

Mount, D. M. and Wu, Y., 2002. An efficient k-means

clustering algorithm: Analysis and implementation.

vol 24, pages 881–892, july.

Niku S. B., 2001. Introduction to Robotics, Analysis,

Systems, Applications. Prentice Hall.

Poppe, R.W. and Poel, M., 2005. Example-based pose

estimation in monocular images using compact fourier

descriptors. CTIT Technical Report series TR-CTIT-

05-49 Centre for Telematics and Information

Technology, University of Twente, Enschede. ISSN

1381-3625

Roy, S.D., Chaudhury, S. and Banerjee. S., 2004. Active

recognition through next view planning: a survey.

Pattern Recognition 37(3):429–446, March.

Sipe M. and Casasent, D., 2002. Feature space trajectory

methods for active computer vision. IEEE Trans

PAMI, Vol. 24, pp. 1634-1643, December.

ACTIVE 3D RECOGNITION SYSTEM BASED ON FOURIER DESCRIPTORS

325