DECENTRALIZED APPROACH FOR FAULT DIAGNOSIS OF

DISCRETE EVENT SYSTEMS

Moamar Sayed Mouchaweh

, Alexandre Philippot

and Véronique Carré-Ménétrier

Université de Reims, CReSTIC, Moulin de la Housse 51687 Reims - France

LURPA, ENS de Cachan, 61 avenue du Président Wilson, 94235 Cachan Cedex, France

Keywords: Fault diagnosis, Discrete Event Systems, Decentralized diagnosis, Co-diagnosability notion.

Abstract: This paper proposes a decentralized approach to realize the diagnosis of Discrete Event Systems (DES).

This approach is based on a set of local diagnosers, each one of them diagnoses faults entailing the violation

of the local desired behavior. These local diagnosers infer the fault’s occurrence using event sequences, time

delays between correlated events and state conditions, characterized by sensors readings and commands

issued by the controller. An adapted codiagnosability notion is formally defined in order to ensure that the

set of local diagnosers is able to diagnose all faults entailing the violation of the global desired behavior. An

example is used to illustrate the proposed approach.

1 INTRODUCTION

Manufacturing systems are too large to perform a

centralized diagnosis. Moreover, they are

informationally and geographically decentralized.

Thus a diagnosis module with a decentralized

structure is the most adapted one for this kind of

systems. However, the challenge of decentralized

diagnosis methods is to perform local diagnosis

equivalent to the centralized one. Indeed, the partial

observation of the system may lead to an ambiguity

of the final diagnosis decision. Examples of DES

decentralized diagnosis methods can be found in

(Debouk, 2000), (Pandalai, 2000), (Qiu, 2005), and

the references therein.

Failure diagnosis in DES requires that once a

failure is occurred, it must be detected and isolated

within a bounded delay or number of events. This

property is verified using a notion of diagnosability.

This notion can be formalized differently according

to whether the fault is modelled as the execution of

certain faulty events, event-based notion, or as the

consequence of reaching at certain faulty states,

state-based notion. In (Sampath, 1994), an event-

based diagnosability notion is defined. The system

model is based on a finite-state automaton. This

notion defines a diagnoser that uses the history of

events to detect the occurrence of a failure.

Consequently, a system is diagnosable if and only if

any pair of faulty/non-faulty behaviors can be

distinguished by their projections to observable

behaviors. The event-based diagnoser can diagnose

actuator and sensor permanent and intermittent

failures. However, the diagnoser and the system

model must be initiated at the same time to allow the

system model and diagnoser to response

simultaneously to events. This initialization is hard

to obtain in manufacturing systems since their initial

state may not be known. To enhance the

diagnosability, the above framework is extended to

dense-time automata (Tripakis, 2002). This

extension is useful since it permits to model plants

with timed behavior.

In (Pandalai, 2000), an event-based approach is

proposed to monitor manufacturing systems. In this

approach, the timed sequence events, generated by

the DES, is compared with a set of specifications of

normal functioning called templates. These

templates are based on the notion of expected event

sequencing and timing relationships. They are

suitable for modelling processes in which both

single-instance and multiple-instance behaviors are

exhibited concurrently. However, these templates do

not allow the analysis of diagnosability properties,

which are based on a diagnosability notion.

To find a remedy to the initialization problem, a

state-based diagnosability notion is proposed in (Lin,

1994), (Zad, 2003). In this notion, since the system

states describe the conditions of its components,

124

Sayed Mouchaweh M., Philippot A. and Carré-Ménétrier V. (2007).

DECENTRALIZED APPROACH FOR FAULT DIAGNOSIS OF DISCRETE EVENT SYSTEMS.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 124-129

DOI: 10.5220/0001627301240129

 SciTePress

diagnosing a fault can be seen as the identification in

which state or set of states the system belongs to.

However, the diagnosis is limited to the case of

actuator faults. While manufacturing systems use

many sensors entailing the necessity of diagnosing

also their faults.

This paper presents a decentralized diagnosis

approach to perform the diagnosis of manufacturing

systems. The paper is structured as follows. Firstly,

the different steps of the proposed approach

necessary to construct the local diagnosers are

detailed. Secondly, a timed-event-based

diagnosability notion is presented. Then, in order to

verify the codiagnosability property of local

diagnosers, this notion is extended to the

codiagnosability notion. Finally, a simple example is

used to illustrate the proposed approach.

2 DECENTRALIZED DIAGNOSIS

APPROACH

2.1 System Boolean Models

We use Boolean DES (BDES) modelling, introduced

in (Wang, 2000), to model the equipments (sensors

and actuators) behavior of the system. The system

model G consists of n local models: G

,…, G

, each

one owns its local observable events responsible of a

restricted area of the process. G

= (Σ, Q, Y,

, h, q

)

is represented as Moore automaton and L = L(G)

denotes its corresponding prefixed closed language.

Σ is a set of finite observable and unobservable

events. Q is the set of states, Y is the output space,

x Q

→

Q is the state transition function and Σ

the set of all event sequences of the language L(G).

(

, q) provides the set of possible next states if

occurs at q. h: Q

→

Y is the output function and

h(q) is the observed output at q.

q is the initial

state.

Let Σ

= {

,…,

} be the set of fault

partitions. Each fault partition,

, j ∈ {1, 2,…, r},

corresponds to some kind of faults in an equipment

element (sensor or actuator). We assume at most one

fault may occur at a time. These faults must be

considered when BDES models.

In (Balemi, 1993), Balemi et al. defined

controllable events Σ

⊆ Σ as controller’s outputs

sent to actuators, and uncontrollable events Σ

⊆ Σ

as the controller’s inputs coming from sensors. (Σ

∪ Σ

) ⊂ Σ is the set of observable events. The

unobservable events are failure events or other

events which cause changes not recorded by sensors.

Let G

and its corresponding prefixed closed

language, L

= L(G

), be the local model of the

restricted area of the system observed by this model.

= (Σ

, Q

, Y

, h

, q

) is represented as Moore

automaton. Σ

= Σ

∪ Σ

is the set of local

observable events by G

and Σ

⊂ Σ

. The other

notations have the usual definition but for the

restricted area observed by G

G observes the system by one global projection

function or mask, P

: Σ

∪ {

} → Σ

, where Σ

the set of all observable event sequences observed

by G. The inverse projection function is defined as:

-1

(u) = {s ∈ L: P

(s) = u}. Similarly, a local

projection function can be defined for each local

model G

as: P

: Σ

∪ {

} → Σ

Each state q

of G is represented by an output

vector h

considered as a Boolean vector whose

components are Boolean variables. Let d denote the

number of state variables of G, the output vector h

of each state q

can be defined as:

∀q

∈ Q, h(q

) = h

= (h

,…, h

), h

∈ {0, 1},

1 ≤ j ≤ 2

, h

∈ Y ⊆

A transition from one state to another is defined

as a change of a state variable from 0 to 1, or from 1

to 0. Thus each transition produces an event

characterized by either rising,

= ↑h

, or falling,

↓h

, edges where p ∈ {1, 2,…, d}.

To describe the effect of the occurrence of an

event

∈ Σ

, a displacement vector E

= (e

,…,

,…, e

is used. If e

= 1, then the value of p

state variable h

will be set or reset when

occurs.

While if e

= 0, the value of p

state variable h

will remain unchanged:

Ehh)q,(q,,Qq,q

ijijoji

⊕=⇒

∈

∀

∈

∀

(1)

The set of all the displacement vectors of all the

events provides the displacement matrix E. For each

event

∈ Σ

, an enablement condition, en

) ∈ {0,

1}, is defined in order to indicate if the event

can

occur at the state q

, en

) = 1, or not:

))q(en.E(hh)q,(q,,Qq,q

iijijoji

αα

⊕=⇒

∈

∀

∈

∀

(2)

2.2 Constrained-System Boolean Model

Let S = (Σ, Q

, Y,

, h, q

) denote the constrained-

system model, characterized as Moore automaton. It

defines the global desired behavior of the system

and it is represented by the prefixed closed

specification language K = L(S) ⊆ L(G). S can be

obtained using different algorithms from the

literature as the ones developed in (Philippot, 2005),

DECENTRALIZED APPROACH FOR FAULT DIAGNOSIS OF DISCRETE EVENT SYSTEMS

125

(Ramadge, 1987) and the references therein. To

obtain the transition function

, the enablement

conditions for all the system events at each state

must satisfy all the specifications K, representing the

desired behavior:

))q(en.E(hh,)q(en

)q,(q,Qq,q,

iiji

iSjSji

ααα

⊕==

⇒=∈∀∈∀

(3)

Each local model G

has a local constrained

model S

, which is a part of the global constrained

model S. S

is represented by the specification

language K

= L(S

), which is included in K. S

Moore automaton: S

= (Σ

, Q

, Y

, h

, q

) and Q

⊂ Q

. All these notations have the usual definition

but for the local constrained-system model S

2.3 Codiagnosability Notion

2.3.1 Basic Definitions

Let

define the set of all the event sequences

ending by a fault belonging to the fault partition

Thus

)(

= ∪

denotes the set of all the event

sequences ending by a fault belonging to one of fault

partitions of Σ

. Consequently

⊆ (L - K), i.e., all

the faulty sequences are considered as violation of

the specification language K. The set of faulty states

is defined as S

)S(

j 1=

∪

where S

is the set of

states reached by the occurrence of a fault of F

. Let

denote the set of all state output vectors of the

faulty states belonging to S

. Then the output

partition H

can be defined as:

∀q’ ∈ S

, h’ = h(q’) ⇒ h’ ∈ H

The set of fault labels Λ

= {F

, F

,..., F

}

indicates the occurrence of a fault belonging to one

of the fault partitions Σ

. By adding the normal label

N, we can obtain the set Λ of all the labels used by

the diagnoser. We define the label function l: Q → Δ

to indicate the functional status of the system when

it reaches a state q ∈ Q. Δ is the set of all possible

subsets of the diagnoser labels:

{}{ }{ } { }

{

}{ }

{}{}{ }{ }

F,...,F,N,...,F,F,N,F,N,...,F,N

,F,...,F,F,F,F,F,...,F,F,N

⎭

⎬

⎫

⎩

⎨

⎧

1211

212121

Similarly, we can define Δ

as the set of all the

subsets of fault labels.

2.3.2 Events Timing Delays Modelling

The majority of sensors and actuators in

manufacturing systems produce constrained events

since state’s changes are usually effected by a

predictable flow of materials (Pandalai, 2000).

Therefore, we define a set of expected consequents

for each controllable event,

∈

, in order to

predict uncontrollable but observable consequent

events within pre-defined time periods. This EC

describes the next events that should occur and the

relative time periods in which they are expected.

These pre-defined time periods are determined

by experts according to the system dynamic and to

the desired behavior. If u =

βα

...

is an

observable event sequence starting by a controllable

event

, and ending by the observable event

sequence

...

uok

Σ⊂

ααα

, then the set of expected

consequents

)(uEC

is created when the event

occurs.

)(uEC

has the following form: )(uEC

{

}

C,...,C,...,C,C

is a consequent expected

after the enablement of the controllable event

and

it is defined as follows:

{

}

),],[,(,,

max

min

lttqC ij

ααα

. It means that when

occurs, the event

should happen at the state

and within the interval [

min

max

]. If it is the case

then the expected consequent is satisfied. If the

event

has occurred before

min

or after

max

then

the expected consequent is not satisfied and it

provides the fault label

∈ , as the cause of

this non-satisfaction. This set of expected

consequent

)(uEC

is evaluated by a function

)(uEF

. )(uEF

is equal to 1 if one of its expected

consequents is not satisfied while it is equal to zero

if all its expected consequents are satisfied.

2.3.3 Codiagnosability Notion Formulation

If a system composed of n local diagnosers with a

global closed prefixed language L, a global closed

prefixed specification language K, a global

projection function P, and a predefined set of fault

partitions, Σ

= {

,…,

}, is diagnosable

using a central diagnoser. Then this system is F-

codiagnosable according to the projection functions,

: i = 1 … n, if and only if :

{

}

{}

FlstPEFm,...,,z

Hhqhh,q,uq,Qq

)KL(u

KLstPPu,kt,n,...,,i

,KLst,r,...,,j,f,INk

==⇒∈∃

∈

′

⇒

′

∈∀

∩−∈⇒

⎥

⎦

⎤

−∩∈∀≥∈∃

∩−∈∀∈∈∀∈∃

−

and1))((21

)()(

)()(21

)(21

ΨΠ

(4)

The satisfaction of (4) means that the occurrence

of a fault of the type F

is diagnosable by at least one

local diagnoser D

, using the event-based, state-

based or timed local models. Indeed if the faulty

event sequence s, ending by a fault of the type F

, is

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

126

distinguishable by the central diagnoser D after the

execution of k = |t| transitions, where t is a

continuation of s. If u is any other event sequence

belonging to (L – K) and producing the same

observable event sequence as st, P

(u) = P

(st),

according to the local diagnoser D

. Then the system

is F-codiagnosable if and only if:

• u contains in it a fault of the type F

, (event-

based model),

• u transits D

to a state characterized by an output

vector belonging to the output partition H

(state-based model),

• There is at least one expected consequent,

defining a temporal constraint between the

occurrence of the observable events P

(st) by the

diagnoser D

, not satisfied. This expected

consequent is evaluated by an expected function

which provides a fault label l = {F

} as the cause

of this non-satisfaction, (timed-model).

2.3.4 Codiagnosability Checking

The set of local diagnosers are able to diagnose any

fault belonging to one of the fault partitions of F and

within a finite delay, if:

{}

1)(,,...,2,1,, =⇒∈∃∈∀∈∈∀ qenQqniKL

ρρ

(5)

{} {}

{}

Fl(PEFqenQq

,n,...,,i,,r,...,,j,KL,L

===⇒∈∃

∈∃≠∩∈∀−∈∈∀

and)1))(or0)((

2121

ϕψρρρ

(6)

Nk ∈≤

(7)

(5) means that all the enablement conditions of

all the local diagnosers must be satisfied for any

event of a sequence belonging to the global desired

behavior. Thus this condition ensures that no

conflict can occur between local diagnosers for the

enablement of events at any state of the desired

behavior. The satisfaction of (6) ensures that any

event sequence violating the global desired behavior,

due to the occurrence of a fault of the type F

, must

be diagnosed by at least one local diagnoser D

when

it reaches the state q. This detection and isolation are

based on the non-satisfaction either of the

enablement condition of the latest event in the event

sequence

or of its expected function. In the both

cases, this non-satisfaction should provide the fault

label F

. Finally (7) guarantees that this diagnosis

decision will be realized in a finite delay equal to the

cardinality of the event sequence

3 ILLUSTRATION EXAMPLE

3.1 Example Presentation

We monitor a wagon with an electric actuator with

two senses of movement: right and left, obtained by

two commands, R for the movement right and L for

the movement left. Three sensors a, b and c are used

to indicate the wagon location in, respectively, A, B

or C, as it is illustrated in Figure 1. We have chosen

this simple example for easy understanding. The

same reasoning can be followed for the application

of the approach on more complex examples.

L R

a b

AB A-B

C B-C

Figure 1: Illustration example.

The following hypotheses must hold:

• The wagon inertia is null,

• Actuator does not fail during operation, i.e., if it

does fail, the fault is at the start of operation,

• There are no ambiguity or indecision cases

between the local diagnosers.

The system is modelled with two sub models: G

and G

. Their local observable events are

respectively: Σ

= {↑R, ↓R, ↑L, ↓L, ↑a, ↓a, ↑b, ↓b}

and Σ

= {↑R, ↓R, ↑L, ↓L, ↑b, ↓b, ↑c, ↓c}. We use

five Boolean state variables a, b, c, R and L to

describe the overall wagon behavior G. a, b and c

are true when the wagon is located respectively in A,

B or C.

Each local model consists of two components:

the wagon motor behavior and the change of the

wagon location measured by the sensors a and b for

, and b and c for G

. The set of fault partitions to

be diagnosed is F = {F

, F

}. F

, F

and

indicate, respectively, sensor a, sensor b, sensor c

and wagon motor stuck-on or stuck-off.

3.2 Constrained System Models

The constrained-system model S for the wagon

example is depicted in Figure 2 and is provided by

the user. S

and S

represent the local desired

behaviors for the two sub models G

and G

according to their set of local observable events.

In BDES modelling, this desired behavior can be

described using two tables; the first one explains the

enablement conditions for the occurrence of each

event and the second one is the displacement matrix

for the estimation of the state output vector of each

DECENTRALIZED APPROACH FOR FAULT DIAGNOSIS OF DISCRETE EVENT SYSTEMS

127

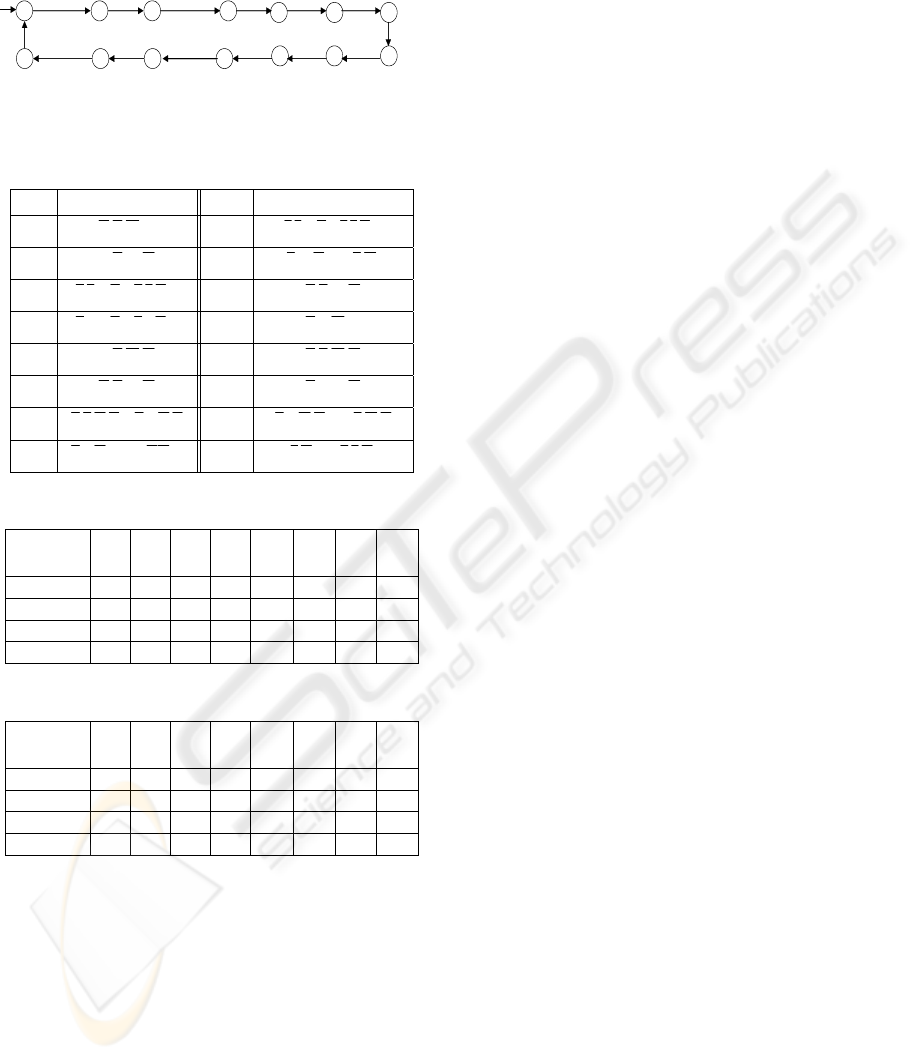
next state. These tables are shown respectively in

Table 1, Table 2 and Table 3 for S

and S

1 2

↑ R

14 13

↑a

3 4

↑b

12 11

↑ L

↓

: a

10000 10010 0001

01010

01000 10001 00001 01001

5 6

9 8

↑b

↑c

↑

↓

0001

00110 00100

001010000101001

Figure 2: Global constrained-system model S .

Table 1: The enablement conditions for S

and S

σ: S

↑a

LRba ...

↑b

LRcbLRcb ...... +

↓a

LRba ...

↓b

LRcbLRcb ...... +

↑b

LRbaLRba ...... +

↑c

LRcb ...

↓b

LRbaLRba ...... +

↓c

LRcb ...

↑R

LRba ...

↑R

LRcb ...

↓R

LRba ...

↓R

LRcb ...

↑L

LRbaLRba ...... +

↑L

LRcbLRcb ...... +

↓L

LRbaLRba ...... +

↓L

LRcbLRcb ...... +

Table 2: The displacement matrix E

for S

State

variable

↑a ↓a ↑b ↓b ↑R ↓R ↑L ↓L

a 1 1 0 0 0 0 0 0

b 0 0 1 1 0 0 0 0

R 0 0 0 0 1 1 0 0

L 0 0 0 0 0 0 1 1

Table 3: The displacement matrix E

for S

State

variable

↑b ↓b ↑c ↓c ↑R ↓R ↑L ↓L

b 1 1 0 0 0 0 0 0

c 0 0 1 1 0 0 0 0

R 0 0 0 0 1 1 0 0

L 0 0 0 0 0 0 1 1

3.3 Expected Consequents Definition

Two expected consequents are defined for G, one for

each command enablement: EC

↑R

, EC

↑L

. The

enablement of R, entails the events

↓a, ↑b, ↓b, and ↑c

to occur respectively at the states q

, q

, and q

↓a is expected to occur within the time period [1,2],

after the enablement of R,

↑b within the time period

[3,5] after the occurrence of

↓a, ↓b inside the

interval [1,2], and

↑c inside [3,5] according to the

system dynamic. If

↓a does not occur at q

then the

wagon motor has not responded. Thus the non-

satisfaction of the corresponding expected

consequent at this state indicates the occurrence of a

fault belonging to

. If ↓a has occurred, then S

will transit to the state q

. If ↑b has not occurred,

then the non-satisfaction of the corresponding

expected consequent provides the label l = {F

} to

indicate that the sensor b is faulty, stuck-off, since

the wagon has responded. Similarly the non

occurrence of

↓b at q

indicates that the sensor b is

stuck-on. Consequently EC

↑R

can be written:

↑

{

}{ }

{}{}

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

↑↓↓↑

)F],,[,q(,c,b,)F],,[,q(,b,b

,)F],,[,q(,b,a,)F],,[,q(,a,R

3524

2342

5321

Similarly the expected consequent for the

enablement of the command L can be written:

↑

{

}{ }

{}{}

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

↑↓↑↓

↓↑↓↑

)]53[(]53[

)]21[()]21[(

29113

41248

F,,,q,b,c,F,,,q(,a,b

,F,,,q,b,L,F,,,q,c,L

3.4 Local Diagnosers Construction

Two local diagnosers D

and D

are constructed for

the sub models S

and S

. Each local diagnoser

contains, besides the states of the local desired

behavior model, all the faulty states that can be

reached by the occurrence of a fault belonging to

one of the fault partitions. Each one of these faulty

states is reached due to the non-satisfaction either of

the enablement condition of an event or of an

expected consequent. This makes the diagnoser

declaring a fault. The diagnosers D

and D

are

depicted respectively in Figure 3 and Figure 4. Each

diagnoser state is determined by testing whether the

enablement condition, or the expected consequent, is

satisfied (the next state is a desire one) or not (the

next state is faulty). The fault labels are calculated

by determining the reason of the non-satisfaction.

The diagnoser can be initiated at any state

distinguished by its output vector, i.e., the states

with the dotted entrant arrows. If the diagnoser is

initiated at any state distinguished by an event, the

diagnoser cannot diagnose a past occurrence of a

fault. As an example, the faulty states reached by an

unsatisfied expected consequent cannot be

distinguished from the ones of the desired behavior

if the diagnoser was initiated at one of these states.

The system is F-codiagnosable if it satisfies the

conditions (5), (6) and (7). The condition (5) is

satisfied since the two diagnosers authorize both the

events observable by them:

,q∀ 0.

≠

↑↑ bb

enen and

≠

↓↓ bb

enen

. The condition (6) is also verified

since the local diagnosers can diagnose with

certainty the occurrence of a fault belonging to one

of the fault partitions of Σ

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

128

diagnoses with certainty the faults belonging

to one of

and

while D

diagnoses with

certainty the faults belonging to one of

and

. Finally (7) holds since the delay required to

diagnose a fault belonging to one of the fault

partitions, in the worst case and for any one of the

two diagnosers, is finite and equal to 6 events. If we

consider the non-satisfaction of an expected

consequent as an event then starting from any

diagnoser state of the desired behavior, the longest

event sequence required to decide the occurrence of

a fault is maximally equal to 6. As an example,

starting from the state 7 of D

, the detection of the

occurrence of a fault belonging to one of

requires, respectively, 6 events (state 21), 5

events (state 20) and 5 events (state 19). Thus, the

system is F-codiagnosable.

1110

↑

↓

↑

↓

↑

0010

1000

N,F

1010

N,F

0010

N,F

0110

N,F

0010

N,F

0000

N,F

1010

abRL

0110

1101

↓

↑

0001

N,F

0101

N,F

0100

N,F

0101

N,F

0001

N,F

1001

N,F

↓

↑

↓

1010

↑

(

↓

↑

)=1

↑

(

↑

↓

b)=1

↑

(

↓

↑

b)=1

↑ R

(

↑

↓

a)=1

↑ R

(

↓

↑

b)=1

Figure 3: Local event-state-based diagnoser, D.

1110

0001

↑ R

↑ b ↓ b ↑ c ↓ R

↑ L ↓ b

↑ L

↑c

1010

0000

N,F

0010

N,F

1010

N,F

0010

N,F

0110

N,F

0100

N,F

0101

N,F

0001

N,F

1110

bcRL

1001

N,F

1000

N,F

1001

N,F

0001

N,F

↑ b ↓ c

0010

↓ L

1001

↑ b

0101

↑

(↑ L↓ b)=1

↑

(↓ c↑ b)=1

↑

(↓ b↑ b)=1

↑

(↓ b↑ c)=1

↑

(↑ L↓ c)=1

Figure 4: Local event-state-based diagnoser, D

4 CONCLUSIONS

In this paper, a decentralized diagnosis approach is

proposed to diagnose manufacturing systems. This

approach is based on several local diagnosers. They

diagnose together faults, which violate the

specification language representing the desired

behavior of the monitored system.

A simulation tool based on Stateflow of Matlab

is constructed in order to test and validate the

proposed approach on application examples. This

tool is based on a library of component models to

design and to test the performances of diagnosis

module for different applications.

We are developing a distributed diagnosis

module to perform the diagnosis of manufacturing

systems. This module uses the timed-event-state-

based diagnoser, proposed in this paper, as a local

diagnoser in a distributed structure.

REFERENCES

Balemi S, Hoffmann G.J., Gyugyi P, Wong-Toi H.,

Franklin G.F. Supervisory control of a rapid thermal

multiprocessor, IEEE Transactions on Automatic

Control, vol. 38, n°7, pp. 1040-105, 1993.

Debouk R., Lafortune S., and Teneketzis D. Coordinated

decentralized protocols for failure diagnosis of DES,

Discrete Event Dynamic Systems: Theory and

Applications, 10(1-2):33–86, 2000.

Lin F., Diagnosability of Discrete Event Systems and its

Applications, In Discrete Event Dynamic Systems4,

Kluwer Academic Publishers, USA. 1994.

Pandalai D., L. E. N. Holloway, Template Languages for

Fault Monitoring of Timed Discrete Event Processes,

In IEEE Transactions On Automatic Control 45( 5),

2000.

Philippot A., Sayed Mouchaweh M., Carré-Ménétrier V.,

Multi-models approach for the diagnosis of Discrete

Events Systems, In IMACS’05, International

conference on Modelling, Analyse and Control of

Dynamic Systems, Paris-France, 2005.

Qiu W., Decentralized/distributed failure diagnosis and

supervisory control of DES, PhD Thesis, the Iowa

State University, USA, 2005.

Ramadge P., Wonham W., Supervisory control of a class

of discrete event processes, In SIAM J. Control Optim.

25(1), 1987.

Sampath M., Segupta R., Lafortune S., Sinnamohideen K.,

Teneketzis D., Diagnosability of discrete event

systems, In 11

Int. Conf. Analysis Optimization of

Systems: DES, France, 1994.

Tripakis S., Fault Diagnosis for Timed Automata, 7th

International Symposium on Formal Techniques in

Real Time and Fault Tolerant Systems (FTRTFT’02),

Oldenburg Germany, 2002.

Wang Y., Supervisory Control of Boolean Discrete-Event

Systems, Thesis of Master of Applied Sciences,

University of Toronto, Canada, 2000.

Zad S. H., Kwong R. H., Wonham W. M., Fault Diagnosis

in DES: Framework and model reduction, IEEE

Transactions On Automatic Control 48(7), 2003.

DECENTRALIZED APPROACH FOR FAULT DIAGNOSIS OF DISCRETE EVENT SYSTEMS

129