NEW RESULTS ON DIAGNOSIS BY FUZZY PATTERN

RECOGNITION

Mohamed Saïd Bouguelid, Moamar Sayed Mouchaweh and Patrice Billaudel

Centre de Recherche en Science et Technologie de l’Information (CReSTIC),Université de Reims-Champagne-Ardennes

Moulin de la Housse, BP 1039, 51687 Reims, France

Keywords: Pattern recognition, Fuzzy pattern matching, Nearest Neighbours techniques, Multi-criteria decision.

Abstract: We use the classification method Fuzzy Pattern Matching (FPM) to realize the industrial and medical

diagnosis. FPM is marginal, i.e., its global decision is based on the selection of one of the intermediate

decisions. Each intermediate decision is based on one attribute. Thus, FPM does not take into account the

correlation between attributes. Additionally, FPM considers the shape of classes as convex one. Finally the

classes are considered as equi-important by FPM. These drawbacks make FPM unusable for many real

world applications. In this paper, we propose improving FPM to solve these drawbacks. Several synthetic

and real data sets are used to show the performances of the Improved FPM (IFPM) with respect to classical

one as well as to the well known classification method K Nearest Neighbours (KNN). KNN is known to be

preferment in the case of data represented by correlated attributes or by classes with different a priori

probabilities and non convex shape.

1 INTRODUCTION

In statistical Pattern Recognition (PR) (Dubuisson,

2001), historical patterns about system functioning

modes are divided into groups of points, called

classes, using unsupervised learning method (Duda,

2001) or human experience. These patterns, or

points, with their class assignments, constitute the

learning set. A supervised learning method uses the

learning set to build a classifier that best separates

the different classes in order to minimize the

misclassification error. This separation, or

classification, is realized by using a membership

function, which determines the likelihood or the

certainty that a point belongs to a class.

The membership function can be generated using

Probability Density Function (PDF) estimation

based methods or heuristics-based ones. In the first

category, the membership function is equal to either

the PDF or to the probability a posterior. The

estimation of PDF can be parametric, as the baysien

classifier (Dubuisson, 1990), or non parametric, as

the Parzen window (Dubuisson, 2001), voting k

nearest neighbour rules (Denoeux, 1998), (Denoeux,

2001) and (Dubuisson, 2001), or by histograms

(Sayed Mouchaweh, 2004), (Medasani, 1998). In

heuristic-based methods (Medasani, 1998), the shape

of the membership function and its parameters are

predefined either by experts to fit the given data set,

or by learning to construct directly the decision

boundaries as the potential functions (Dubuisson,

1990) and neural networks (Ripley, 1996), or the

clustering methods as Fuzzy C-Means (Medasani,

1998).

One of the applications of PR is the diagnosis of

industrial systems for which no mathematical or

analytical information is available to construct a

model about the system functioning. Each

functioning mode, normal or faulty, is represented

by a class. The problem of diagnosis by PR becomes

a problem of classification, i.e., the actual

functioning mode can be determined by knowing the

class of the actual pattern, or observation, of the

system functioning state.

There are many fuzzy classification methods in

the literature. The choice of one of them depends on

the given application and the available data. We use

the method Fuzzy Pattern Matching (FPM)

(Devillez, 2004b), (Grabish, 1992) and (Sayed

Mouchaweh, 2002a) because it is simple, adapted to

incomplete database cases and has a small and

constant classification time. FPM is a marginal

classification method, i.e., its global decision is

167

Saïd Bouguelid M., Sayed Mouchaweh M. and Billaudel P. (2007).

NEW RESULTS ON DIAGNOSIS BY FUZZY PATTERN RECOGNITION.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 167-172

DOI: 10.5220/0001628401670172

 SciTePress

based on the selection of one of the intermediate

decisions. Each intermediate decision is calculated

using a membership function based on a probability

histogram for each class according to each attribute.

Thus, FPM is not adapted to work with data

represented in a space of correlated attributes.

Additionally, it does not respect the shape of classes

if this shape is non convex. Finally, all the classes

are considered as equi-important, i.e., with the same

a priori probabilities.

In this paper we propose a solution to develop

FPM to take into account the correlation between

attributes as well as the class importance and its

shape if this shape is non convex. The paper is

structured as follows. Firstly, the functioning of

FPM is explained briefly. Then the limits of FPM

are discussed using some synthetic examples. Next,

several real examples are used to evaluate the

performances of the Improved FPM (IFPM) with

respect to the classical one as well as to the well

known classification method K Nearest Neighbours

(KNN). This evaluation is based on the

misclassification rate. Finally a conclusion ends this

paper.

2 FUZZY PATTERN MATCHING

FPM, described in (Devillez, 2004b), (Grabish,

1992) and (Sayed Mouchaweh, 2002a), is a

supervised classification method based on the use of

probability histograms. Let C

, C

, …, C

denote the

classes described by a attributes. These attributes

provide different points of view about the

membership of an incoming point in the different

classes. The functioning of FPM involves two

phases: the learning and the classification ones.

2.1 Learning Phase

In the learning phase, the data histograms are

constructed for each class according to each

attribute. The number of bins h for a histogram is

experimentally determined. This number has an

important influence on the performances of FPM

(Sayed Mouchaweh, 2002b). The histogram upper

and lowest bounds can be determined either as the

maximal and minimal learning data coordinates or

by experts. In this paper, we adopted the first

manner and we have added a tolerance Tol to adjust

this histogram in order to maximize FPM

performances. The height of each bin is the number

of learning points located in this bin. The probability

distribution

p of the class C

according to the

attribute j is calculated by dividing the height of

each bin b

by the total number N

of learning points

belonging to the same class. Then these probabilities

{

}

{

}

hkyp

,...,2,1,)( ∈ are assigned to bins

centres

. The PDF

P is obtained by a linear

linking between the bins heights centres. Indeed if

we have a large number of data, the normalized

histogram can be assumed to approximate the PDF.

In order to take into account the uncertainty and

the imprecision contained in the data, the probability

distribution

p is converted into possibility one

This conversion is realized using the transformation

of Dubois and Prade (Dubois, 1993) defined as:

∑

dkk

yp,ypminy ))()(()(

(1)

We have chosen this transformation for the good

results which it gives in PR applications (Sayed

Mouchaweh, 2002b), (Sayed Mouchaweh, 2006). A

linear linking between bins heights centres converts

the distribution of possibilities

{

}

{

}

hky

,...,2,1,)( ∈

into density one

. This

operation is repeated for all the attributes of each

class.

2.2 Classification Phase

The membership function

for each class C

and

according to each attribute j is considered to be

numerically equivalent to the possibility distribution

(Zadeh, 1978). Thus, the classification of a new

point x, whose values of the different attributes are

, …, x

, is made in two steps:

 Determination of the possibility membership

value

of the point x to each class C

according to the attribute j by a projection on

the corresponding possibility density

;

 Merging all the possibility values

, ...,

concerning the class C

, into a single one by an

aggregation operator H:

),...,(

1 a

iii

πππ

(2)

The result

of this fusion corresponds to the

global possibility value that the new point x belongs

to the class C

. The operator H can be a

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

168

multiplication, a minimum, an average, or a fuzzy

integral (Grabish, 1992). Finally, the point x is

assigned to the class for which it has the maximum

membership value.

3 LIMITS OF FPM

3.1 Classes of Non Convex Shape

FPM is similar to the naive Bayesian classifier who

supposes the attributes statistically independent.

This classifier defines the probability a

posterior

()

CxΦ that x belongs to the class C

by:

j=1

() ( )()

iii

Cx pxCPCΦ=

∏

(3)

Where

()

px C is the marginal conditional density

of the attribute j given the class C

and P(C

) denotes

the a priori probability of the class C

. If the a priori

probabilities of classes are the same, then the

equation (3) becomes similar to the equation (2).

Thus FPM, as all the other marginal methods, does

not take into account neither the correlation between

attributes nor the class importance or its shape if it is

non convex. Indeed, FPM produces always

rectangular membership level curves for all the

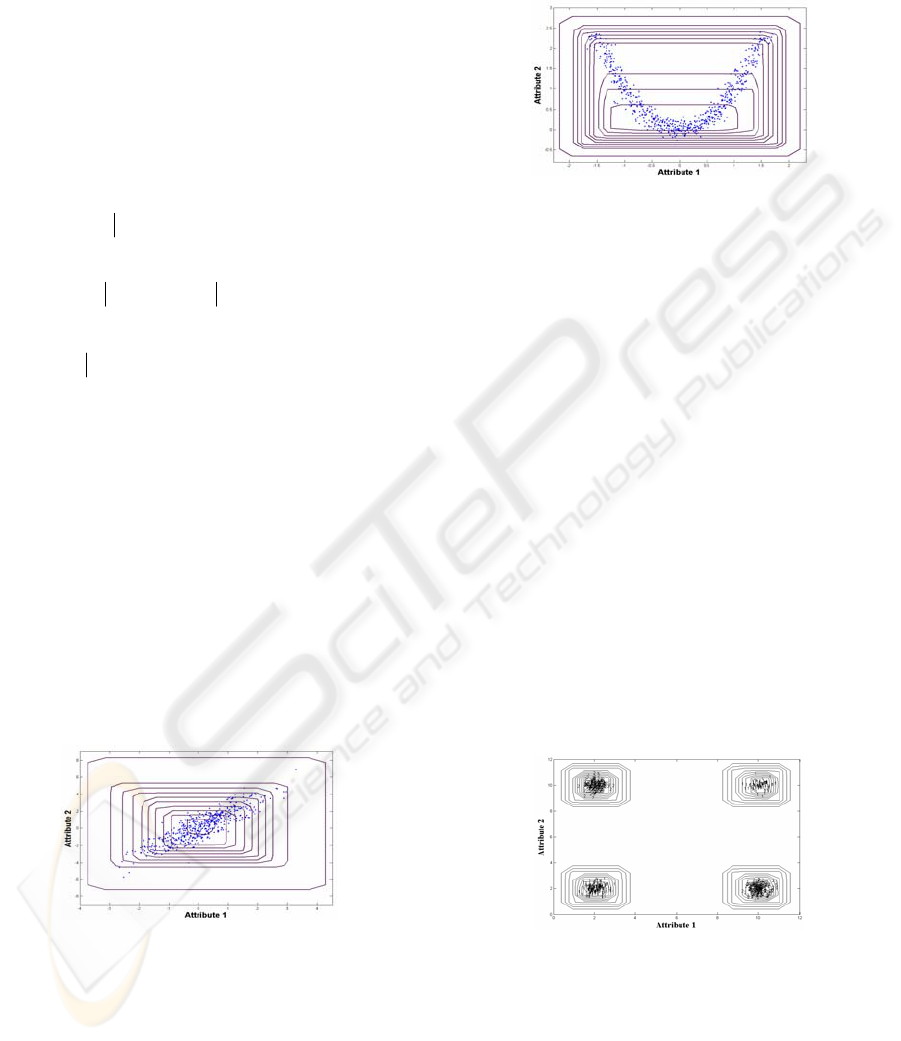
possible class shapes. Figure 1.a and Figure 1.b

present respectively the membership level curves

obtained by FPM for a class defined either by two

linear or non linear correlated attributes. We can

notice that these levels do not respect the class

shape.

Figure 1.a: Membership level curves obtained by FPM for

a class defined by linear correlated attributes.

In (Devillez, 2004a), two improvements were

proposed to integrate the information about class

shape in the learning phase. These two

improvements are based on the division of each

class into several sub ones. However these

improvements have some drawbacks as the critical

determination of the value of some parameters, like

the number of subclasses, the expensive computation

time and the rejection areas inside classes, i.e., areas

in which points are not assigned to any class.

Figure 1.b: Membership level curves obtained by FPM for

a class defined by non linear correlated attributes.

3.2 Classes with Correlated Attributes

The XOR data are a classical example used in the

literature to show the correlation between attributes.

Indeed any classifier needs to use the information

issued from all the attributes to take a correct

decision. Thus FPM is not adapted for this type of

data since its decision is based on the selection of

one attribute. The Figure 2 shows XOR data in a

representation space of two attributes as well as the

membership level curves, obtained by FPM for the

class 1. We can see that the classes have a convex

shape and that FPM does not distinguish between

the points of the class 1 and the ones of the class 2.

Thus the improvements proposed by Devillez

(Devillez, 2004a) cannot solve this problem since

they were developed to be adapted to the class shape

and not to the case of correlated attributes. Same

remark can be noticed for the membership level

curves of the class 2.

Figure 2: The membership level curves, obtained by FPM,

for XOR data for the class 1.

In (Cadenas, 2004) a solution to make FPM

operant in the case of data with correlated attributes

is presented. This solution uses the Parzen Window

method to construct the membership functions of

each class according to one main feature and, if it is

necessary, to one auxiliary feature. The

NEW RESULTS ON DIAGNOSIS BY FUZZY PATTERN RECOGNITION

169

classification phase uses the fuzzy integral as an

aggregation operator. However, this solution is

consuming of time and has an exponential

complexity according to the number of attributes. In

addition, this solution does not work in the case of

XOR described by more than two attributes.

4 IMPROVED FPM (IFPM)

We propose a solution to make FPM operant in the

case of data with correlated attributes and classes of

non convex shape. This solution looks for the

relationship between the attributes of the

representation space using the learning set. This

relationship is represented by a correlation matrix

between the bins of the histogram of the first

attribute and all the other bins of the other

histograms of the other attributes. This solution does

not require any determination of any supplementary

parameter. The functioning of IFPM is divided into

two phases: learning and classification ones.

4.1 Learning Phase

The learning phase of IFPM is similar to the one of

FPM but it integrates in addition the information

about the zones of learning points inside the

representation space. Each zone is resulting by the

intersection of the bins of a learning point according

to all attributes.

Let X denotes the learning set which contains N

points x divided into c classes inside a representation

space of a attributes. Each class C

contains n

points:

{1,2,..., }ic∈ . Each histogram for each

attribute j,

{1,2,..., }ja∈ , contains h bins

b ,

{1, 2 , ..., }

kh∈ . The correlation matrix B for the

learning set X is defined as follows:

],...,,...,,[

21 ci

BBBBB =

(4)

Where

B is the correlation matrix for the class

. This matrix can be calculated as follows:

{

}

[1,0]

=∈

(5)

Where x belongs to the zone resulting by the

intersection of the bins

[, ,..., ]

xkk k

bbb b= .

the correlation factor between the bin

b of the first

attribute and all the other bins of the other attributes

according to the class C

. This correlation factor can

be calculated using the following equation:

,() :

XCx C

∀

∈=

1213 1

If ... 1

Else 0

kkkk kk b

xb b b b b b

⎧

∈

∩∧∩∧∧∩⇒ =

⎪

⎨

⇒=

⎪

⎩

(6)

Where “

∧

” and “

∩

” denote respectively the AND

and intersection operators.

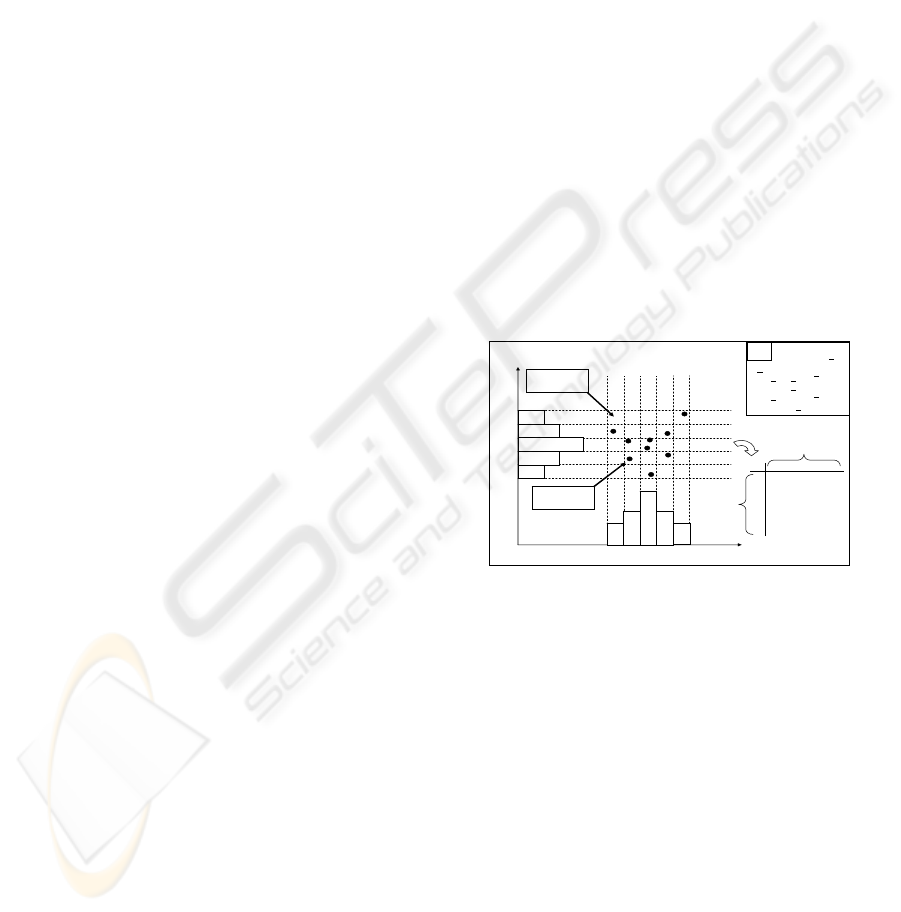
The Figure 3 shows a simple example of the

calculation of the matrix B for the case of a

representation space containing one class defined by

two attributes. We can notice that the bins

b and

b are correlated because a learning point is located

in the zone resulting by the intersection of these two

bins. Thus the correlation factor of this zone

equal to 1 in the matrix B. While there is no learning

point in the zone of the intersection of the bins

and

b . The correlation factor of this zone

equal to zero in B.

⎥

⎦

⎤

⎢

⎣

⎡

10000

01010

00101

00110

01000

Figure 3: Correlation Matrix obtained by IFPM for the

class

C inside

ℜ

4.2 Classification Phase

The classification of a new point x starts by

determining its bins according to each attribute

[ , ,..., ].

xkk k

bbb b= Then the possibility membership

value

for each class C

is calculated exactly as

FPM if and only if

. In order to take onto

account the importance of a class, the possibility of

each class is multiplied by its a priori probability. If

,0=

the point x will be rejected according to the

class

, i.e., 0

. Finally the point x will be

assigned to the class for which it has the highest

possibility membership value. The Figure 4

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

170

represents the steps of the classification phase of

IFPM

Classification by IFPM

[ ,..., ,..., ]

xk k k

bb b b=

Calculating by FPM the

membership value

Rejecting the point

according to the class

→

= 0

Yes

Finding the correlation factor in

the matrix

For each class

i =

,…,

ic= ic=

Determination of the bins

of the

point

according to each attribute

(,, , )

xxx= ……

New point:

Assigning

to the class for which it

has the maximum membership value

Yes

∑

Figure 4: Algorithm of the classification phase of IFPM.

The Figure 5.a and Figure 5.b show the

membership level curves issued from the application

of IFPM on the two examples of the Figure 1.

Figure 5.a: Membership level curves obtained by IFPM

for a class defined by linear correlated attributes.

Figure 5.b: Membership level curves obtained by IFPM

for a class defined by non linear correlated attributes.

We can find that these curves respect the non

spherical and non convex shapes of classes.

Equally, the Figure 6 shows these curves for the

class 1 obtained by IFPM, for XOR data. We can

find that IFPM discriminates well the points of the

class 1 and the class 2. Same result can be obtained

for the class 2.

Figure 6: Membership level curves, obtained by IFPM, for

XOR data for class 1.

5 EXPERIMENTAL RESULTS

We will test the performances of IFPM with FPM

and classical as well as Fuzzy KNN (FKNN) with

crisp initialisation and several values of k between 1

and 15, using the misclassification rate as evaluation

criterion. For that we use four data sets: XOR

problem, Spiral, Pima Indians diabetes (Newman,

1998) and Ljubljana Breast Cancer (LBC) data sets

(Newman, 1998). XOR problem data set is

composed of 2 classes in a representation space of 5

attributes. We have chosen 5 attributes to test IFPM

performances in the case of a representation space

characterized by more than 2 correlated attributes.

Spiral data are represented in terms of evenly spaced

samples from a non linear two-dimensional

transformation of the Cartesian coordinates. We

have chosen this data set because the classes are non

linearly separable. The Pima and LBC data sets are

known to be strongly non Gaussian. The number of

points in each class, the number of classes and the

number of attributes are depicted in Table 1.

We have used the leave-one-out method to

calculate the Misclassification Rate (MR) because it

gives a pessimistic unbiased estimation of MR. We

integrate also the Rejection Rate (RR) to indicate the

number of points which are not assigned to any

class. Indeed, it is better to reject a point than to

misclassify it. The Table 2 shows the obtained

results for the three methods. These results are

obtained using the optimal values of

h and Tol for

FPM and IFPM, and

K for KNN. We can conclude

that IFPM provides better results, according to the

evaluation criterion and for the four data sets, than

FPM and both, KNN and FKNN.

NEW RESULTS ON DIAGNOSIS BY FUZZY PATTERN RECOGNITION

171

Table 1: Data Sets used for the test.

Data set Classes DIM Per Class

XOR 2 5 {400,400}

Spiral

2 2 {970,970}

Pima

2 8 {268,500}

LBC

2 9 {218,68}

Table 2: Comparison between IFPM, FPM, KNN and

FKNN, using leave-one-out technique, according to

Rejection Rate (RR) and to Misclassification Rate (MR).

Method FPM

IFPM

Criterion

MR (%) RR (%)

XOR 44.12 0 0 0

Spiral 18.24 0 0 1.5

Pima 30.73 0.78 19.53 20.7

LBC 25.87 1.05 10.14 30.42

Method KNN FKNN

XOR 0 0 0 0

Spiral 0 0 0 0

Pima 25.26 0 26.43 0

LBC 23.78 0 23.43 0

6 CONCLUSIONS

In this paper, we have proposed a solution to adapt

the classification method Fuzzy Pattern Matching

(FPM) to be operant in the case of classes with

correlated attributes as well as the class importance

and its shape if this shape is not convex. The

integration of this solution in FPM is called

Improved FPM (IFPM). The performances of IFPM

are compared with the ones of FPM, K Nearest

Neighbours (KNN) and Fuzzy KNN (FKNN) using

the misclassification rate as evaluation criterion.

This comparison is realized according to four data

sets. We have also used XOR problem and Spiral

data which are widely used to study the correlation

between attributes. In addition, we have used Pima

Indians diabetes and Ljubljana Breast Cancer data

sets which are known to be strongly non Gaussian

with different a priori probabilities. The

misclassification rate obtained by IFPM is better

than the one of FPM, KNN and FKNN. However,

IFPM rejects more points than the previous methods.

Anyway, it is better to reject a point than to

misclassify it.

REFERENCES

Cadenas, J.M., M.C. Garrido and J.J. Hernandez, 2004.

Improving fuzzy pattern matching techniques to deal

with non discrimination ability features. In: IEEE

International Conference on Systems, Man and

Cybernetics, pp. 5708-5713.

Denoeux, T., M. Masson and B. Dubuisson, 1998.

Advanced pattern recognition techniques for system

monitoring and diagnosis: a survey. In: Journal

Européen des Systèmes Automatisés (RAIRO-APII-

JESA), Vol. 31(9-10), pp. 1509-1539.

Denoeux, T. and L.M. Zouhal, 2001. Handling

possibilistic labels in pattern classification using

evidential reasoning. In: Fuzzy Sets and Systems, Vol.

1(22), pp. 409-424.

Devillez, A., 2004a. Four supervised classification

methods for discriminating classes of non convex

shape. In: Fuzzy sets and systems, Vol. 141, pp. 219-

240.

Devillez, A., M.Sayed Mouchaweh and P. Billaudel,

2004b. A process monitoring module based on fuzzy

logic and Pattern Recognition. In: International

Journal of Approximate Reasoning, Vol. 37, Issue 1,

pp.43-70.

Dubois, D. and H. Prade, 1993. On possibility/probability

transformations, In: Fuzzy Logic, pp. 103-112.

Duda, R.O., P.E. Hart and D.E. Stork, 2001. Pattern

Classification second edition. Wiley, New York

Dubuisson, B., 2001. Automatique et statistiques pour le

diagnostic. Traité IC2 Information, commande,

communication. Hermes Sciences, Paris.

Dubuisson, B., 1990. Diagnostic et reconnaissance des

formes, Traité des Nouvelles Technologies, série

Diagnostic et Maintenance, Hermes Sciences, Paris.

Grabish, M. and M. Sugeno, 1992. Multi-attribute

classification using fuzzy integral. In: Proc. of fuzzy

IEEE, pp. 47-54.

Medasani, S., K. Jaeseok and R. Krishnapuram, 1998, An

overview of membership function generation

techniques for pattern recognition. In: International

Journal of Approximate Reasoning,Vol. 19,pp. 391-

417.

Newman D.J., Hettich, S., Blake C.L. and Merz, C.J,

1998. UCI Repository of machine learning databases,

http://www.ics.uci.edu/~mlearn/MLRepository.html,

Dept. of Information and Computer Science,

University of California, Irvine.

Ripley, B.D.,1996. Pattern Recognition and Neural

Networks. Cambridge University Press, Cambridge.

Sayed Mouchaweh, M., A. Devillez, G.V. Lecolier and P.

Billaudel, 2002a. Incremental learning in real time

using fuzzy pattern matching. In: Fuzzy Sets and

Systems, Vol. 132/1, pp. 49-62.

Sayed Mouchaweh, M. and P. Billaudel ,2002b. Influence

of the choice of histogram parameters at Fuzzy Pattern

Matching performance. In: WSEAS Transactions on

Systems, Vol. 1, Issue 2, pp. 260-266

Sayed Mouchaweh, M., 2004. Diagnosis in real time for

evolutionary processes in using Pattern Recognition

and Possibility theory. In: International Journal of

Computational Cognition 2, Vol. 1, pp. 79-112.

Zadeh, L. A., 1978. Fuzzy sets as a basis for a theory of

possibility. In: Fuzzy sets and systems, Vol. 1, pp. 3-2.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

172