BAYESIAN ADAPTIVE SAMPLING FOR BIOMASS

ESTIMATION WITH QUANTIFIABLE UNCERTAINTY

Pinky Thakkar

Department of Computer Engineering, San Jose State University, San Jose, CA 95192, USA

Steven M. Crunk, Marian Hofer, Gabriel Cadden, Shikha Naik

Department of Mathematics, San Jose State University, San Jose, CA 95192, USA

Kim T. Ninh

Department of Computer Engineering, San Jose State University, San Jose, CA 95192, USA

Keywords: Adaptive Sampling, Bayesian Inference, BRDF, Maximum Entropy, Optimal Location Selection.

Abstract: Traditional methods of data collection are often expensive and time consuming. We propose a novel data

collection technique, called Bayesian Adaptive Sampling (BAS), which enables us to capture maximum

information from minimal sample size. In this technique, the information available at any given point is

used to direct future data collection from locations that are likely to provide the most useful observations in

terms of gaining the most accuracy in the estimation of quantities of interest. We apply this approach to the

problem of estimating the amount of carbon sequestered by trees. Data may be collected by an autonomous

helicopter with onboard instrumentation and computing capability, which after taking measurements, would

then analyze the currently available data and determine the next best informative location at which a

measurement should be taken. We quantify the errors in estimation, and work towards achieving maximal

information from minimal sample sizes. We conclude by presenting experimental results that suggest our

approach towards biomass estimation is more accurate and efficient as compared to random sampling.

1 INTRODUCTION

Bayesian Adaptive Sampling (BAS) is a

methodology which allows a system to examine

currently available data in order to determine new

locations at which to take new readings. This

procedure leads to the identification of locations

where new observations are likely to yield the most

information about a process, thus minimizing the

required data that must be collected. As an example

of the application of this methodology, we examine

the question of standing woods in the United States.

In order to estimate the amount of carbon

sequestered by trees in the United States, the amount

of standing woods must be estimated with

quantifiable uncertainty (Wheeler, 2006). Such

estimates come from either satellite images or near

ground measurements. The amounts of error in the

estimates from these two approaches are currently

unknown. To this end, an autonomous helicopter

with differential GPS (Global Positioning System),

LIDAR (Light Detection and Ranging), stereo

imagers, and spectrometers has been developed as a

testing platform for conducting further studies

(Wheeler, 2006). These instruments are capable of

measuring the reflectance data and the location of

the Sun and helicopter in terms of the zenith and the

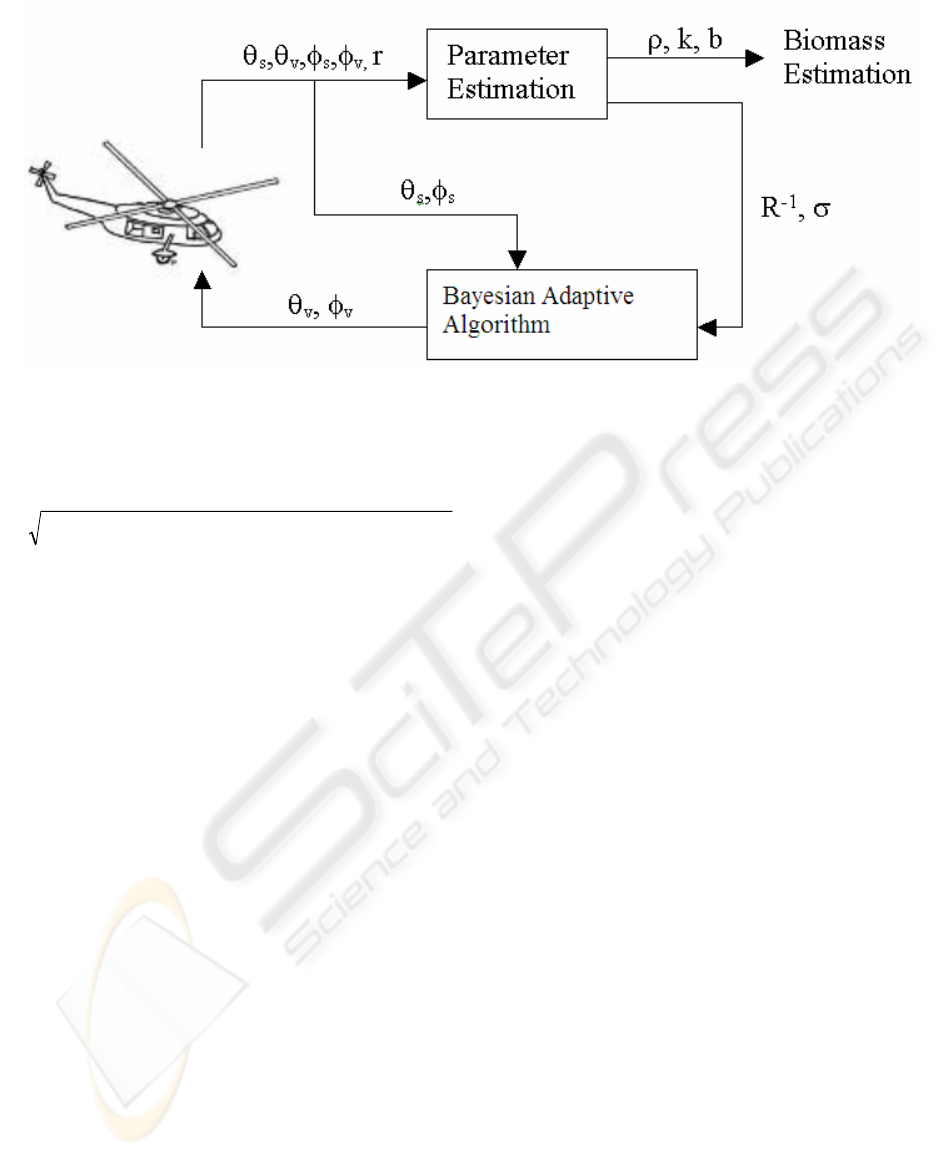
azimuth angles (Figure 1). The objective is to

develop a controlling software system for this

robotic helicopter, which optimizes the required

ground sampling.

The first simplistic data collection method is to

conduct an exhaustive ground sampling i.e. to send

the helicopter to every possible location. The second

approach is to perform random sampling until the

estimates have acceptable standard errors. Although

random sampling presents a possibility that the

229

Thakkar P., M. Crunk S., Hofer M., Cadden G., Naik S. and T. Ninh K. (2007).

BAYESIAN ADAPTIVE SAMPLING FOR BIOMASS ESTIMATION WITH QUANTIFIABLE UNCERTAINTY.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 229-236

DOI: 10.5220/0001628702290236

 SciTePress

helicopter will take samples from the locations that

offer the greatest amount of information and

therefore reduce the needed sample size, there is no

guarantee that such a sample set will be chosen

every time. The third and more efficient method is to

take only a few samples from “key” locations that

are expected to offer the greatest amount of

information. The focus of this paper is to develop a

methodology that will identify such key locations

from which the helicopter should gather data.

Figure 1: θ

, φ

are the zenith and the azimuth angles of

the Sun, and θ

, φ

are the zenith and the azimuth angles

of the view, respectively (Wheeler, 2006).

In the work described here, the key locations are

identified using current and previously collected

data. The software works in tandem with the

sampling hardware to control the helicopter’s

position. Once a sample has been taken, the data are

fed into the system, which then calculates the next

best location to gather further data. Initially, the

system assumes an empirical model for the ground

being examined. With each addition of data from the

instruments, the parameter estimates of the model

are updated, and the BAS methodology is used to

calculate the helicopter’s next position. This process

is repeated until the estimated uncertainties of the

parameters are within a satisfactory range. This

method allows the system to be adaptive during the

sampling process and ensures adequate ground

coverage.

The methodology employs a bi-directional

reflectance distribution function (BRDF), in which

the calculation of the amount of reflection is based

on the observed reflectance values of the object, and

the positions of the Sun and the viewer (Nicodemus,

1970). The advantage of using this function is that it

enables the system to compensate for different

positions of the Sun during sampling. Once the

reflectance parameters are estimated, BAS uses the

principle of maximum entropy to identify the next

location where new observations are likely to yield

the most information.

In summary, the BAS methodology allows the

system to examine currently available data with

regards to previously collected data in order to

determine new locations at which to take new

reflectance readings. This procedure leads to the

identification of locations where new observations

are likely to yield the most information.

2 RELATED WORK

Computing view points based on maximum entropy

using prior information has been demonstrated by

Arbel et al., 1970. They used this technique to create

entropy maps for object recognition. Vazquez et al.,

2001 also demonstrated a technique for computing

good viewpoints; however their research was based

on Information Theory. Whaite et al., 1994

developed an autonomous explorer that seeks out

those locations that give maximum information

without using a priori knowledge of the

environment. Makay, 1992 used Shannon’s entropy

to obtain optimal sample points that would yield

maximum information. The sample points are taken

from the locations that have largest error bars on the

interpolation function. In our work, the optimal

locations that offer maximum amount of information

are identified using the principle of maximum

entropy, where the maximization is performed using

techniques suggested by Sebastiani et al., 2000.

3 MODEL

The model for the data used in our framework is

based on the semi-empirical MISR (multi-angle

imaging spectrometer) BRDF Rahman model

(Rahman et al., 1993):

[]

()

(,,,)

cos( ) cos( ){cos( ) cos( )}

exp ( ) ( , , , )

svsv

sv s v

svsv

bp h

θφφ

ρθ θ θ θ

θθφφ

−

+⋅

−⋅ Ω ⋅

(1)

where

(,,,)1

1(,,,)

svsv

vsv

θθφφ

θφφ

−

(2)

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

230

)cos()tan()tan(2)(tan)(tan

),,,(

vsvsvs

vsvs

φφθθθθ

−−+

(3)

)cos()sin()sin()cos()cos()(

vsvsvs

−

+=Ω

(4)

where

),,,(

vsvs

is the measured reflectance,

is the surface reflectance at zenith, k is the

surface slope of reflectance,

b is a constant

associated with the hotspot, or "antisolar point" (the

point of maximum reflectivity, which is the position

where the sensor is in direct alignment between the

Sun and the ground target),

, are the zenith and

the azimuth angles of the Sun, respectively (Figure

1), and

, are the zenith and the azimuth angles

of the view, respectively (Figure 1).

4 METHODOLOGY

Our framework consists of the following two steps:

1. Parameter Estimation: In this step, we

estimate the values of the parameters (

k and b ), and their covariance matrix and

standard errors, given the data collected to

date of the amount of observed reflected

light, and the zenith and azimuth angles of

the Sun and the observer.

2. Bayesian Adaptive Sampling (Optimal

Location Identification): In this step, we

use the principle of maximum entropy to

identify the key locations from which to

collect the data.

Once the key location is identified, the helicopter

goes to that location and the instruments on the

helicopter measure the reflectance information. This

information is then fed into the Parameter

Estimation stage and the new values of the

parameters (

, k and b ) are calculated. This

process is repeated until the standard errors of the

parameters achieve some predefined small value,

ensuring adequacy of the estimated parameters

(Figure 2).

5 IMPLEMENTATION

5.1 Parameter Estimation

The input to this module is the observed reflectance

value (r), zenith and azimuth angles of the Sun

),(

, and zenith and azimuth angles of the

observer

),(

. The parameters (

, k and b )

are estimated using the following iterated linear

regression algorithm:

First, a near linear version of this model is

accomplished by taking the natural logarithm of

),,,(

vsvs

, which results in the following

Figure 2: Overview of Bayesian Adaptive Sampling.

BAYESIAN ADAPTIVE SAMPLING FOR BIOMASS ESTIMATION WITH QUANTIFIABLE UNCERTAINTY

231

equation:

[]

),,,(ln)(.

)}cos()){cos(cos()cos(ln

)1(ln),,,(ln

vsvs

hpb

φφθθ

θθθθ

+Ω−

⋅−+=

(5)

Note that aside from the term

),,,(ln

vsvs

, which contains a nonlinear

, the function ln(r) is linear in all three

parameters,

)ln(

, k , and b . “Linearization” of

)ln(h is accomplished by using the value of

from the previous iteration, where at iteration n in

the linear least-squares fit

),,,(

vsvs

is taken

to be the constant

),,,(1

1),,,(

)1(

)(

vsvs

φφθθ

−

(6)

where

)0(

is set equal to zero.

Second, regression is performed on our linearized

model to calculate the estimates of the following

quantities:

•

, k and b , the parameters

•

1−

, covariance matrix of the estimated

parameters (

, k and b )

•

, the standard deviation of the errors,

(which are assumed to be independent

identically distributed random variables from

a normal distribution with zero mean)

Third, the current estimated value of

is then

used in

),,,(

vsvs

, and regression is again

performed.

This procedure is repeated until the estimate

converges.

5.2 Bayesian Adaptive Sampling

This module identifies the best informative location

),(

to which to send the helicopter. We employ

the principle of maximum entropy, in which the

available information is analyzed in order to

determine a unique epistemic probability

distribution. The maximization is performed as per

techniques suggested by Sebastiani et al., 2000,

where in order to maximize the amount of

information about the posterior parameters, we

should maximize the entropy of the distribution

function. Mathematically, maximizing the entropy is

achieved by maximizing

log[ ( ) ]XXR

−

′

Σ+

(7)

where ∑ is covariance matrix of the error terms,

1−

is covariance matrix of the estimates of the

parameter

, k and b , and X is matrix of input

variables where each row in X is associated with one

observation

[

]

1 xxX

(8)

where

[]

)}cos()){cos(cos()cos(ln

vsvs

θθθθ

)cos()sin()sin(

)cos()cos()(

vsvs

φφθθ

−+

−

Under the assumption that the errors are

independent normally distributed random variables

with mean zero and variance

, (7) reduces to

maximizing

(

)

−

′

XRXI

. (9)

Note that

and

1−

are estimated in module 1

and are thus at this stage assumed to be known

quantities. The matrix X contains both past

observations, in which case all elements of each

such row of X are known, and one or more new

observations where the zenith and the azimuth

angles of the Sun

),(

are known, so the only

remaining unknown quantities in (9) are the values

and

(the zenith and azimuth angles of the

helicopter viewpoint) in rows associated with new

observations. Thus, the new location(s) to which the

helicopter will be sent are the values of

and

in rows of X associated with new observations that

maximize (9).

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

232

6 EXPERIMENT

We conduct two simulated experiments in which the

estimates of the model parameters are calculated. In

the first experiment, “Estimation Using Random

Observations”, the data is collected by sending the

helicopter to random locations. In the second

experiment, “Estimation using BAS”, the data is

collected using BAS.

The experiments are conducted under the

following assumptions:

• The view zenith angle (

) is between 0 and

, and the view azimuth angle (

) is

between 0 and 2

( ≈ 6.283185).

• The Sun moves 2

radians in a 24-hour

period, i.e., at the rate of slightly less then

0.005 radians per minute.

• It takes about 2 minutes for the helicopter to

move to a new location. Thus, the position of

the Sun changes approximately 0.01 radians

between measurements.

In our simulation, the true values of the

parameters

and

are 0.1, 0.9, and -0.1,

respectively. For the purpose of this paper, the

observed values were simulated with added noise

from the process with known parameters. This

allows us to measure the efficacy of the algorithm in

minimizing the standard errors of the parameter

estimates, and also the estimates of the parameters.

In actual practice, the parameters would be

unknown, and we would have no way of knowing

how close our estimates are to the truth, that is, if the

estimates are as accurate as implied by the error

bars.

6.1 Estimation using Random

Observations

In this experiment, we send the helicopter to 20

random locations to collect data. Starting with the

fifth observation, we use the regression-fitting

algorithm on the collected input data set (the

observed reflectance information, and the positions

of the Sun and the helicopter), to estimate the values

of the parameters

as well as their standard

errors. Table 1 shows the results of this experiment

6.2 Estimation using BAS

In this experiment, the first five locations of the

helicopter are chosen simultaneously using an

uninformative prior distribution (i.e., as no estimate

1−

has yet been formed; it is taken to be

)

and an X matrix with five rows in which the position

of the Sun

),(

is known and (9) is maximized

over five pairs of helicopter viewpoints

and

Subsequently, we use BAS to calculate the next

best informative location for the helicopter to move

to in order to take a new reflectance observation., in

which case the X matrix contains rows associated

with previous observations, and (9) is maximized

over a single new row of the X matrix in which the

position of the Sun

),(

is known and the only

unknowns are a single pair of helicopter viewpoint

values,

and

, in the last row of the X matrix.

Table 2 shows the results from this experiment.

In both experiments, estimates of the parameters,

along with their standard errors, cannot be formed

until at least five observations have been taken.

7 RESULTS

In this section, we compare and analyze the results

of our two experiments. The comparison results

(Figure 3, Figure 4 and Figure 5) show that the

estimates using the data from the "well chosen"

locations using BAS are closer to the true values,

9.0

and

1.0

−

, than the estimates based

on data from the randomly chosen locations. Also,

the error bars using BAS are much shorter indicating

higher confidence in the estimates of the parameters

based on the "well chosen locations", i.e., the length

of the error bar for the estimate calculated using

data/observations from five well chosen locations is

as short as the error bar based on data collected from

20 random locations.

Within each figure (Figure 3, Figure 4 and Figure

5), the horizontal axis indicates the number of

observations between five and twenty that were used

in forming the estimates. The vertical axis is on the

scale of the parameter being estimated. Above each

observation number, an "o" represents the estimate

(using the data from the first observation through the

observation number under consideration) of the

parameter using the randomly chosen locations and

the observations from those locations. The "x"

represents the estimate of the parameter using

observations taken at locations chosen through BAS.

BAYESIAN ADAPTIVE SAMPLING FOR BIOMASS ESTIMATION WITH QUANTIFIABLE UNCERTAINTY

233

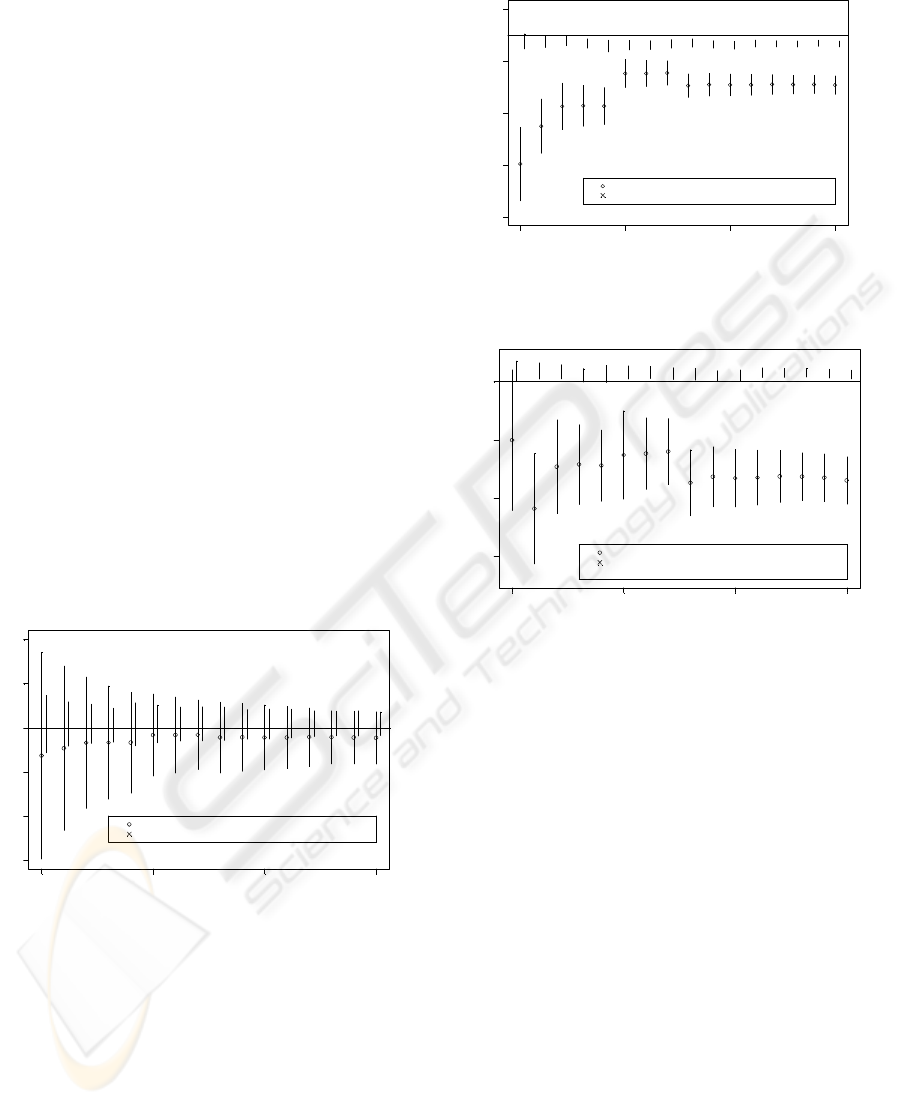
The error bars are the standard errors of the

estimated parameter based on these observations

taken at "well chosen locations". The "bar" is the

error bar, which extends one standard error above

and below the parameter estimate. The horizontal

line represents the true value of the parameter in our

simulation.

Note that in Figure 4 and Figure 5, the error bars

rarely overlap the true value of the parameter. This

can be attributed to two factors. In large part, this is

due to the fact that they are "error bars" with a

length of one standard error beyond the point

estimate. Traditional 95% statistical confidence

intervals based on two standard errors would in

virtually every case overlap the true values.

Additionally, these are cumulative plots, in which

the same data is used, adding observations to form

the parameter estimates as one moves to the right in

each figure. Thus the point estimates and error bars

are dependent upon one another within a figure.

Finally, we see that the estimates using BAS (to

select the points from which to take observation) are

generally closer to the truth than when we use

random points to take observations, and more

importantly the standard errors associated with any

given number of observations are much smaller.

Number of included observations

5 101520

-0.05 0.0 0.05 0.10 0.15 0.20

Using random locations to take observations

Using locations identified by BAS to take observations

Figure 3: Estimates and error bars for

Number of included observations

5 101520

-0.8 -0.6 -0.4 -0.2 0.0

Using random locations to take observations

Using locations identified by BAS to take observations

Figure 4: Estimates and error bars for

Number of included observations

5101520

0.75 0.80 0.85 0.90

Using random locations to take observations

Using locations identified by BAS to take observations

Figure 5: Estimates and error bars for

8 CONCLUSION

Our initial results have shown that BAS is highly

efficient compared to random sampling. The rate at

which the standard errors, or the error bars, are

reduced is much quicker, and hence the significant

amount of information is found more quickly

compared to other traditional methods. We have also

shown that this methodology performs well even in

the absence of any preliminary data points. Further

simulation has shown evidence that BAS can be

three times as efficient as random sampling. This

efficiency amounts to savings of time and money

during actual data collection and analysis.

In addition to the application discussed in this

paper, the theoretical framework presented here is

generic and can be applied directly to other

applications, such as, military, medical, computer

vision, and robotics.

Our proposed framework is based on the

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

234

multivariate normal distribution. The immediate

extensions of this framework will be:

a) To accommodate non-normal parameter

estimate distributions. As part of our future study,

we intend to employ sampling methodologies using

Bayesian Estimation Methods for non-normal

parameter estimate distributions. and

b) To use cost effectiveness as an additional

variable. In this initial work, the focus was to

identify the viewpoints that would give us the most

information. However, it is not always feasible or

efficient to send the helicopter to this next “best”

location. As part of our future work, we intend to

identify the next “best efficient” location for the

helicopter from which it should collect data.

ACKNOWLEDGEMENTS

This work was done as part of the CAMCOS (Center

for Applied Mathematics, Computation, and

Statistics) student industrial research program in the

Department of Mathematics at San Jose State

University.

This work was supported in part by the NASA

Ames Research Center under Grant NNA05CV42A.

We are appreciative of the help of Kevin Wheeler,

Kevin Knuth and Pat Castle, who while at Ames

suggested these research ideas and provided

background materials.

REFERENCES

Arbel, T., Ferrie, F., “Viewpoint selection by navigation

through entropy maps,” in Proc. 7th IEEE Int. Conf.

on Computer Vision, Greece, 1999, pp. 248–254

MacKay, D., “A clustering technique for digital

communications channel equalization using radial

basis function networks,” Neural Computation, vol.4,

no.4, pp. 590–604, 1992.

Nicodemus, F. E., “Reflectance Nomenclature and

Directional Reflectance and Emissivity,” in Applied

Optics, vol. 9, no. 6, June 1970, pp. 1474-1475.

Rahman, H. B., Pinty, B., Verstaete, M. M., “A coupled

surface-atmosphere reflectance (CSAR) model. Part 1:

Model description and inversion on synthetic data,”

Journal of Geophysical Research, vol.98, no.4, pp.

20779–20789, 1993.

Sebastiani P., Wynn, H. P., “Maximum entropy sampling

and optimal Bayesian experimental design,” Journal of

Geophysical Research, 62, Part1, pp. 145-157, 2000.

Sebastiani, P., and Wynn, H. P.

“Experimental Design to Maximize Information,”

Bayesian Inference and Maximum Entropy Methods

in Science and Engineering: 20th Int. Workshop. AIP

Conf. Proc., Gif sur Yvette, France, vol. 568, pp 192-

203, 2000.

Vazquez, P. Feixas, P., Sbert, M., M., Heidrich, W.,

“Viewpoint selection using viewpoint entropy,” in

Proc. of Vision, Modeling, and Visualization,

Germany, 2001, pp. 273–280.

Whaite, P., Ferrie, F. P., “Autonomous exploration:

Driven by uncertainty,” in Proc. of the Conf. On on

Computer Vision and Pattern Recognition, California,

1994, pp. 339–346.

Wheeler, K. R., "Parameterization of the Bidirectional

Surface Reflectance," NASA Ames Research Center,

MS 259-1, unpublished.

BAYESIAN ADAPTIVE SAMPLING FOR BIOMASS ESTIMATION WITH QUANTIFIABLE UNCERTAINTY

235

Table 1: Observation and Estimates Using Random Sampling.

Table 2: Observations and Estimates using BAS.

Observation

Number

Estimate (se)

Estimate (se) of

1 0.460 0.795 0.172364

2 0.470 0.805 0.177412

3 1.561 3.957 0.161359

4 1.561 0.825 0.183571

5 1.265 3.977 0.129712 0.1041 (0.0325) 0.90904 (0.00879) -0.1249 (0.0290)

6 0.514 0.845 0.173072 0.1042 (0.0252) 0.90927 (0.00700) -0.1255 (0.0233)

7 1.561 3.400 0.160130 0.1045 (0.0223) 0.90857 (0.00615) -0.1220 (0.0199)

8 1.172 4.007 0.130101 0.1029 (0.0192) 0.90547 (0.00577) -0.1329 (0.0180)

9 0.723 0.875 0.189697 0.1039 (0.0244) 0.90663 (0.00748) -0.1428 (0.0228)

10 1.561 0.885 0.192543 0.1042 (0.0213) 0.90801 (0.00569) -0.1394 (0.0185)

11 0.527 0.895 0.172811 0.1042 (0.0193) 0.90796 (0.00523) -0.1392 (0.0172)

12 1.561 4.047 0.164530 0.1044 (0.0193) 0.90696 (0.00519) -0.1343 (0.0167)

13 1.561 4.057 0.164822 0.1046 (0.0190) 0.90636 (0.00505) -0.1314 (0.0161)

14 1.137 4.067 0.131443 0.1038 (0.0169) 0.90483 (0.00471) -0.1365 (0.0148)

15 0.713 0.935 0.183894 0.1042 (0.0169) 0.90538 (0.00480) -0.1397 (0.0149)

16 1.561 0.945 0.192280 0.1048 (0.0163) 0.90777 (0.00427) -0.1333 (0.0136)

17 1.187 4.097 0.134701 0.1047 (0.0146) 0.90757 (0.00399) -0.1340 (0.0125)

18 0.655 0.965 0.176841 0.1048 (0.0140) 0.90779 (0.00385) -0.1349 (0.0120)

19 1.561 4.117 0.168819 0.1049 (0.0142) 0.90694 (0.00388) -0.1321 (0.0120)

20 1.148 4.127 0.132199 0.1045 (0.0132) 0.90617 (0.00373) -0.1349 (0.0114)

Observation

Number

Estimate (se)

Estimate (se) of

1 0.114 1.673 0.157552

2 0.882 6.013 0.156616

3 0.761 0.917 0.192889

4 0.678 1.308 0.180404

5 0.260 0.114 0.152558 0.0683 (0.1172) 0.8497 (0.0607) -0.5958 (0.1413)

6 1.195 2.367 0.146659 0.0767 (0.0932) 0.7906 (0.0476) -0.4506 (0.1040)

7 0.237 2.805 0.149475 0.0830 (0.0746) 0.8268 (0.0404) -0.3745 (0.0893)

8 0.166 1.700 0.155497 0.0832 (0.0641) 0.8286 (0.0345) -0.3722 (0.0788)

9 0.320 2.012 0.154191 0.0831 (0.0572) 0.8277 (0.0307) -0.3735 (0.0713)

10 1.224 4.085 0.129133 0.0917 (0.0465) 0.8369 (0.0381) -0.2483 (0.0539)

11 1.409 3.442 0.135005 0.0917 (0.0431) 0.8380 (0.0309) -0.2481 (0.0503)

12 0.092 1.559 0.154096 0.0920 (0.0394) 0.8398 (0.0285) -0.2462 (0.0471)

13 0.806 0.891 0.200401 0.0888 (0.0402) 0.8129 (0.0284) -0.2952 (0.0453)

14 1.256 5.467 0.147654 0.0891 (0.0385) 0.8181 (0.0259) -0.2914 (0.0433)

15 0.227 1.284 0.155373 0.0889 (0.0368) 0.8169 (0.0248) -0.2919 (0.0418)

16 1.129 5.522 0.148721 0.0889 (0.0354) 0.8174 (0.0236) -0.2918 (0.0402)

17 0.507 5.696 0.150381 0.0891 (0.0333) 0.8183 (0.0225) -0.2904 (0.0380)

18 0.119 4.363 0.142232 0.0890 (0.0302) 0.8181 (0.0207) -0.2908 (0.0357)

19 0.245 0.524 0.151915 0.0889 (0.0299) 0.8172 (0.0205) -0.2901 (0.0355)

20 0.446 2.408 0.144471 0.0884 (0.0297) 0.8149 (0.0204) -0.2930 (0.0354)

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

236