
RPQ: ROBOTIC PROXIMITY QUERIES
Development and Applications
Albert Hernansanz, Xavier Giralt
Research Group On Intelligent Robotics and Systems, Technical University of Catalonia, 08028 Barcelona, Spain
Alberto Rodriguez
Robotics Institute, Carnegie Mellon University, Pittsburgh, PA 15213, USA
Josep Amat
Institute of Robotics and Industrial Informatics, Technical University of Catalonia, 08028 Barcelona, Spain
Keywords:
Collision detection, Proximity queries, Surgical application.
Abstract:
This paper presents a robotic proximity query package (RPQ) as an optimization of the general collision
library PQP (Proximity Query Package) for the detection of collisions and distance computation between
open kinematic chains such as robotic arms. The performance of the o ptimizations to non specific collision
query packages are explained and evaluated. Finally, a robotic assisted surgical application is presented which
has been used as a test bed for the proximity package.
1 INTRODUCTION
One of the most important problems to solve in
robotics is the collision avoidance between a robot
and its environment. A robot should perceive the risk
and have a reactive behavior before an imminent col-
lision occurs. Path planning is a hard computational
problem, so having a fast tool to calculate collisions is
a key factor to decrease the necessary time to gener-
ate safety trajectories. In applications where no path
planning exists, for instance in manual guidance or
teleoperation, a real time collision detector is needed
so as to avoid collisions and to be able to interact with
the environment, for example sliding over a surface.
The knowledge of minimum distances between
robots or objects that share a workspace enables
robots to behave in a predictive way. In the human-
robot interaction field, virtual fixtures can be used
both to prevent collisions and help the human oper-
ator by increasing his performance (Stanisic et al.,
1996). In this kind of applications minimum distance
and collision detection must be known in real time.
A new library: Robotic Proximity Queries (RPQ)
package (Giralt and Hernansanz, 2006) has been
developed to deal with these requirements, using
PQP (UNC, 1999) as the a proximity query engine.
The original package has been used to optimize the
queries when working with open kinematic chains,
like robots. These optimizations have been done with
the aim of improving the time performance of the
generic package and simplifying its use in robotic en-
vironments. A system composed of two robots has
been used as a test bed to show the performance of
the RPQ library.
Finally a robotic assited surgical application that
benefits from RPQ performance is presented. The
application consists of the execution of an assisted
cut of a rigid tissue. The surgeon guides freely the
driller held by a slave robotic arm that avoids unde-
sired drillings by means of virtual protections. With
this application not only proximity queries are shown,
but also the graphical interface and the use of a virtual
robot based on RPQ. More information and videos are
available at http://grins.upc.edu
2 RELATED WORK
During the last years, great efforts have been devoted
to the development of efficient collision detection al-
gorithms due to their wide range of applications, such
as CAD/CAM, manufacturing, robotics, simulation
59
Hernansanz A., Giralt X., Rodriguez A. and Amat J. (2007).
RPQ: ROBOTIC PROXIMITY QUERIES - Development and Applications.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 59-66
DOI: 10.5220/0001629100590066
Copyright
c
SciTePress

and computer animation. A wide study of the perfor-
mance and applicability of such methods can be found
in (B.Geiger, 2000). Proximity query algorithms vary
in terms of their range of applicability and the type
of queries they can solve, mainly collision detection,
minimum distance computation and interpenetrations
modelling. Although most algorithms allow as input
triangulated meshes of 3D points, they differ in the
way those points are pre-processed and represented
internally in order to speed up specific queries.
There is a wide set of methods that rely on Lin-
Canny or Gilbert-Johnson-Keiethi like algorithms for
computing minimum distances between pairs of ob-
jects as I-Collide, Swift, Swift++, SOLID, DEEP. . .,
but they are only applicable to convex polytopes
(S.Ehmann and Lin, 2000; S.Ehmann and Lin, 2001;
Kim et al., 2002; Bergen, 2002). This restriction
makes them inappropriate for RPQ purposes, due to
the need to deal with more general geometric models.
More general collision detection methods usu-
ally base their efficiency on pre-computed represen-
tations by means of hierarchies of bounding volumes.
Their differences rely on the specific type of bound-
ing volumes used, ranging from binary space decom-
positions, spheres trees to oriented bounding boxes
(OBB).
Among this set of algorithms, RAPID and PQP
turn to be those that have both, fewer restrictions
in the range of allowable geometric models and an
easier application programming interface (API). Both
of them use oriented bounding boxes for performing
collision tests, and have similar time performances.
However, the fact that PQP offers a wider range
of queries, including minimum distance computation
and tolerance tests makes PQP the best option for the
proximity queries engine of RPQ, the Robotics Query
Package presented in this paper.
3 LIBRARY DESCRIPTION
The goal of the Robotic Proximity Queries (RPQ) li-
brary is to offer an easy, modular and fast proxim-
ity query package oriented to robotics. As explained
above, the aim of the project was not the development
of a new collision detector, but specialize an existing
one into the robotics field.
As described in section 2, there is a wide set of
general purpose proximity query packages. The crite-
rions used to choose PQP as the best candidate for the
development of RPQ are:
1. Types of proximity queries available.
2. High time performance on proximity queries.
3. Ability to use geometrical models based on trian-
gulated meshes of points.
4. Lack off restrictions on possible geometrical mod-
els.
The PQP library has been developed by UNC Re-
search Group on Modelling, Physically-Based Simu-
lation and Applications and offers three different kind
of queries:
- Collision detection: detecting whether two mod-
els overlap, and optionally, give the complete list
of overlapping triangle pairs.
- Distance computation: computing the minimum
distance between a pair of models.
- Tolerance verification: determining whether two
models are closer or farther than a given tolerance
distance.
RPQ has been implemented in C++ language
and its graphical interface has been developed using
OpenGL. The RPQ library can be easily integrated
into any software application.
The library interface allows non expert program-
mers to use it in an easy manner. The graphical inter-
face is a separate module, allowing the programmer
to decide whether using it or not. Fig. 1 shows the in-
tegration of the library and its graphical interface into
a generic application.
3.1 Class Description
The RPQ library is based on the Object Oriented
paradigm. Focused on this paradigm, and based on
robotic environments, three main classes have been
developed: Scenario, Object and Robot.
3.1.1 Scenario
Scenario is the workspace where the objects cohabit.
Concerning its implementation, Scenario is a class
that contains all the objects (Robots and generic ob-
jects), a global reference frame, and all the methods
necessary to generate the proximity query.
3.1.2 Object
An Object is the minimum entity that exists in a Sce-
nario. There are two types of Objects: simple and
complex. A simple Object is represented by a geo-
metrical model composed of a set of triangles referred
to a frame tied to the Object. The Object has also a
transformation matrix to refer itself to the world refer-
ence frame. A complex Object is an Object composed
of a set of geometrical models with joints (rotational
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
60

or prismatic) between them. Thus, a complex Ob-
ject is an open kinematic chain composed of sub ob-
jects. The transformation matrix M
i
refers subobject
i
to subobject
i−1
. The transformation matrix M
0
refers
the object base (subobject
0
) to the world. The object
stores its own geometrical model. Concerning its im-
plementation, an Object is a class containing the geo-
metrical model, the transformation matrix and a set of
methods to position and to orient itself in space. This
class also contains methods to calculate the different
detail representations of its geometrical model.
3.1.3 Robot
A Robot is a particularization of a complex Object
where each of its links is represented by a simple Ob-
ject. A Robot has a set of functions to make a com-
plex Object as similar as possible to a real robot. For
instance, the spatial relationship between links is de-
scribed using the Denavit-Hartenberg notation. Direct
and inverse kinematics can be calculated considering
the robots own restrictions (joint limitations, config-
urations, etc). Concerning implementation, the class
Robot is derived from the class Object. Robot adds all
the functions that are necessary to control a robot. For
instance joint positioning of the robot (direct kinemat-
ics), position and orientation of its tool center point
(inverse kinematics), change of the robot configura-
tion, joints overshoot . . . These added functions with
respect an Object are very helpful when a new robot is
created or used in robotic applications like simulators,
path planners, etc.
Figure 1: Schema of integration of RPQ into a generic ap-
plication.
3.2 Optimizations
PQP is a generic package that does not use the knowl-
edge of the object’s kinematics. In contrast, RPQ is
oriented to robotics, and the knowledge of robot’s
kinematics is the base of the optimizations that spe-
cialize it. RPQ is designed to answer proximity
queries between two robots or between a robot and
any kind of rigid object.
Three optimizations have been developed and
tested to improve the performance offered by PQP:
• Different resolution levels of object’s representa-
tion
• Collision queries sorted using a Weight Matrix
• Collision Matrix
3.2.1 Different Resolution Levels of Object’s
Representation
Objects can be represented in very different resolu-
tion levels. The idea of this optimization is to use the
simplest representation models (minimum number of
triangles) to discard collisions. The lower the number
of triangles of the geometric model are, the faster the
collision queries are executed.
Three resolution levels are used to represent
robots and two for the rest of objects. The highest res-
olution level is the complete geometrical model. The
second level is the oriented bounding box (OBB) of
each sub object in which a complex object is divided.
The lowest resolution level is the bounding box of the
whole complex object. This level is only defined for
complex objects with more than a sub object, as in
robots with several links. There are other possible in-
termediate resolution levels that can be used, for in-
stance the convex hull. It offers a good ratio between
resolution and the quantity of triangles, although it
does not reduce it as drastically as the low resolution
levels chosen.
This optimization is useful in two different situa-
tions. First, in applications where no high precision is
required, for instance when the precision of the OBB
or the convex hull of each link is enough. The second
situation occurs when the different resolution levels
are used in a complementary manner.
Figure 2: Robot with three resolution level representation:
The geometrical model of each link (L3), the OBB of each
link (L2) and the whole bounding box(L1).
When a collision query is performed, a low to high
resolution level list of collision queries is generated.
RPQ: ROBOTIC PROXIMITY QUERIES - Development and Applications
61

Starting with the lowest resolution level, queries are
generated until any collision can be completely dis-
carded. For instance, if a possible collision between
two 6-DOF robots is studied, the first query is done
between the bounding boxes of each robot. If the col-
lision can not be discarded, then the bounding box of
each link is used. If at this level collisions still can not
be discarded, the geometrical models of each link are
checked. As shown in Fig. 2 a Robot with its three
resolution levels of representation.
A test has been developed for the evaluation of
the performance of the optimizations. It consists on
a couple of virtual robotic arms (Staubli RX60B) that
are placed one close to the other in a scenario. The
geometrical models used for the test are high resolu-
tion (composed of 23012 triangles each). The robots
are placed at a variable distance between them and
the scenario is checked for collisions for an equidis-
tributed set of joint positions in their 6 dof.
This test allows us to study the dependency on the
performance of the proposed improvements in terms
of the probability of collision. This is because, as
shown in Table 1, in the designed test, the closer the
robots are, the greater the number of joint configura-
tions that result in collision.
Table 1: Dependence of the amount of colliding configura-
tions on the distance between robots.
Dist. Joint config. Collis. Not Collis.
robots(m) checked
0,4 9216 4864 4352
0,5 9216 3530 5686
0,6 9216 2500 6716
0,7 9216 1121 8095
0,8 9216 140 9076
Fig. 3 shows the consequences of using differ-
ent resolution levels. When the distance between the
robots increases, the queries solved with the bounding
box of the robot increases, and consequently the time
to solve a collision query between the robot decreases.
If the distance decreases, the best combination is us-
ing levels two and three or only level three.
3.2.2 Collision Queries Sorted using a Weight
Matrix
This optimization is based on two assumptions. The
first one is that the goal of the query is just to know
whether there is a collision or not, but not the number
of them. The second assumption is that the kinematics
and the morphology of the robots are well known.
Given these assumptions, the objective is to find
quickly whether there is collision or not, by means
of minimizing the number of partial collision queries.
Figure 3: Time to solve a collision query between two
Staubli RX60B robots using different resolution levels. L3:
Geometrical model of each link. L2: The OBB of each link.
L1: Bounding box of the robot.
The knowledge of the kinematics and the morphol-
ogy of the robots gives us the possibility of assign-
ing an a priori collision probability to each link of
the robot with respect to the rest of robots and ob-
jects present in the same workspace. During exe-
cution time, these probabilities are automatically up-
dated depending on the result of the collision queries
(Probability increases in case of detecting a collision
and decreases otherwise). Therefore, a weight matrix
C is generated combining the probability of collision
between each pair of objects in the workspace. Each
component c
ij
∈ C verifies c
ij
= P
i
+ P
j
where
P
i
and P
j
are the assigned probability of collision of
Object
i
and Object
j
respectively. These weights de-
termine the order of the collision queries, that is if
c
ij
> c
kt
the collision query between Object
i
and
Object
j
will be generated before Object
k
and Object
t
.
A simple way to assign a collision probability to
the links of a robot is to assign higher probability to
those links that are farther in the kinematic chain, with
respect to the base of the robot.
3.2.3 Collision Matrix
The Collision Matrix is a binary matrix that reflects
the possibility of collision between two objects. If
the collision matrix indicates that a collision between
two objects is impossible, its correspondent collision
query is not performed. Of course, a matrix query is
much less expensive than a collision query in compu-
tational terms.
This optimization improves the performance of
the system when a high number of collision queries
are discarded by the Collision Matrix. Computation-
ally, this condition can be expressed as in equation
(1):
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
62
n · QC > m · QM + k · (QC + QM ) (1)
with n = m + k
where:
n Total number of queries.
m Queries resolved with the Collision Matrix.
k Queries resolved with the Query Collision.
QC Average time to solve a Query Collision.
QM Time to solve a query with the Col. Matrix.
The performance of the Collision Matrix has been
studied using the same test designed for testing the
use of different levels of representation. The results
are shown in Fig. 4. The farther the robots are,
the lower is the number of links that can collide, as
seen in Table 2. Therefore, the higher the number of
queries that are solved with the Collision Matrix. As
it is shown in the figure, using the Collision Matrix
the number of collision queries decreases, so does the
time to solve the query.
Table 2: Dependence of the percentage of collision queries
solved by the collision matrix on the distance between
robots.
Dist. between robots (m) Pairs solved with CM
0,4 4,94
0,6 9,88
0,9 24,69
1,2 64,20
Figure 4: Time necessary to solve a collision query between
two Staubli RX60B robots using the Collision Matrix (CM)
or not (NoCM).
Each one of the optimizations proposed improves
the performance of the original library, PQP. How-
ever, the combined use of all of them improves even
more the global performance of the application.
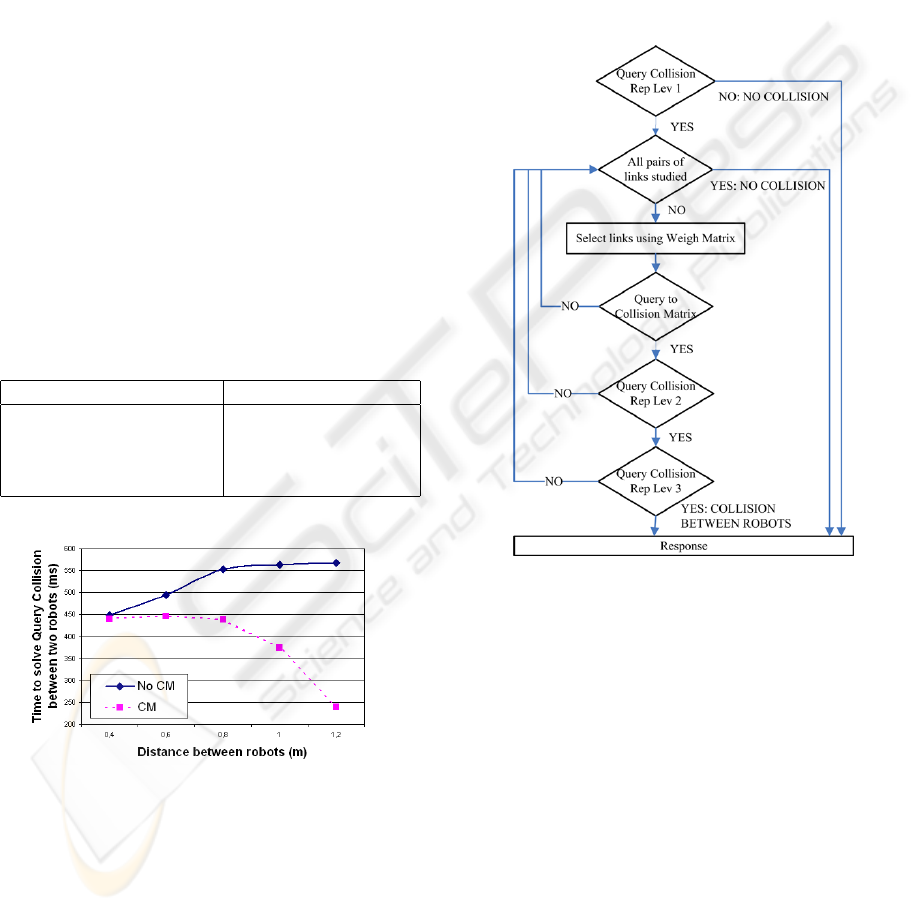
The complete algorithm with all three optimiza-
tions is shown in Fig. 5. First of all, a query colli-
sion between the whole bounding box of both robots
is performed. If at this level the collision cannot be
solved then it is necessary to study collisions among
the whole set of links of both robots. The order in
which these queries must be performed is given by the
Weight Matrix. The query finishes as soon as a colli-
sion appears between a pair of links either in the sec-
ond or third level, or when all pairs have not reported
any collision. For each pair of links, the second and
third representation levels are studied consecutively,
so if a collision is detected in the second level, the
third level has to be studied as well.
Figure 5: Algorithm for collision detection between two
robots using all the optimizations.
4 APPLICATION
One of the advantages of making RPQ generic (al-
though it is optimized for robots) is that this library
can be applied in a wide set of applications. In this
paper a robotic assisted surgical application is pre-
sented. This application has the aim of helping the
surgeon to make a cut on a rigid tissue, for example
in the cranium, avoiding undesired collisions between
the patient and the driller. The surgeon guides freely
the driller that is held by the robot acting in a pas-
sive mode as seen in Fig. 6, allowing all movements
except those which produce undesired collisions.
The system is composed by a Staubli RX60B
robotic arm and a driller. Between the robot and the
RPQ: ROBOTIC PROXIMITY QUERIES - Development and Applications
63

Figure 6: Robotic assisted surgical application.
driller there’s a ATI Multi-Axis Force/Torque Sensor.
The system transforms forces and torques generated
in the driller by the surgeon in new destination points
were the robot must go.
The geometric model of the patient’s cranium is
obtained transforming Computer Tomography data
into a geometrical model composed of triangles.
The surgeon can define the cutting area in the pre-
operative phase and, as will be explained latter, virtual
fixtures are automatically generated to protect the pa-
tient in the operative phase. The possibility of intro-
ducing virtual objects in the scene and the interaction
between them is one of the key factors of RPQ.
The surgeon has a friendly and easy-use graphical
interface that allows the navigation over the virtual
system. This graphical interface helps the surgeon
not only in the pre-operative phase but also during the
surgical operation, providing an augmented reality vi-
sual feedback (collisions, minimal distance between
the cranium and the tool, different points of view of
the scene, virtual fixtures ).
4.1 Surface Navigation
The library developed is useful not only to avoid colli-
sions but also to navigate over an object’s surface. For
instance, the robot tool slides over the surface of the
virtual shield described in section 4.2. This surface
navigation allows the surgeon to feel smooth move-
ments of the robot when the tool is in contact with the
virtual fixtures. The navigation algorithm helps the
surgeon not only avoiding the forbidden regions de-
fined in the pre-operative phase but also guiding him
to the desired cutting path.
The navigation algorithm modifies the position of
the robot tool, but not its orientation. The algorithm is
based on three steps: Knowing the new desired des-
tination of the robot tool, the first step consists of
detecting all collisions between the tool and the ob-
ject’s surface. When all collisions are detected, the
second step consists of projecting the desired point
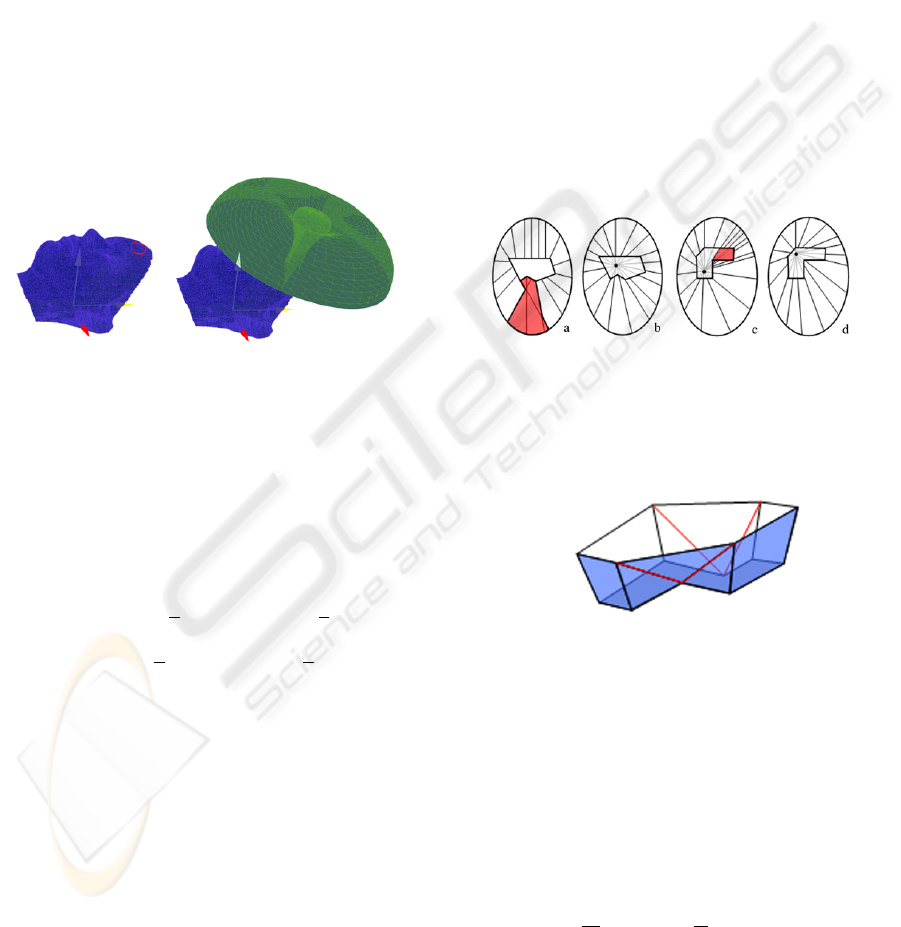
to the plane of the collision triangle, Fig. 7.a. Fi-
nally the projected point that is closer to the desired
one is selected. A problem can occur when the pro-
jected point falls outside the triangle region. In this
situation it is not possible to ensure that this new pro-
jected point is always be outside the object Fig. 7.c.
In this case the new point is projected to the perime-
ter of the triangle. To accomplish this, the outside
region of the triangle is divided into six new regions
(R1, R12, R2, R23, R3, R31), which are defined by
the normals of the edges of the triangle applied to the
vertices of the triangle. The point is then projected
to the closest point of the triangle border of its region
Fig. 7.b. Now, the new destination point is collision
free Fig. 7.d.
Figure 7: Different contact situations between the tool and
a triangle or set of triangles.
4.2 Virtual Protections
Virtual Protections are constraints that rule the be-
haviour of the robot that are specifically designed
to prevent motion into a forbidden region of the
workspace. In this work, the surgeon guides freely
a driller held by the slave robot. The main idea is to
develop a system helpful for the surgeon that prevents
undesired drillings.
4.2.1 Strategy Description
The main goal of the system is to give the robot a re-
active behaviour by means of the definition of virtual
objects in the PQP Scenario with two objectives:
• Protect the patient from the robot and the driller.
• Help the surgeon to locate the desired cutting area.
PQPs ability to check collisions in real time allows
us not only to achieve these objectives but to operate
in an efficient manner.
Throughout a simple interface, in the pre-
operative phase, the surgeon specifies the exact loca-
tion and shape of the cut that must be done. With that
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
64
information, the system generates a shield that covers
the patient while it adapts perfectly to the target area
defined by the surgeon, as shown in Fig. 8.
The proposed behaviour is achieved by the navi-
gation algorithm exposed in chapter 4.1. The system
gives the surgeon the confidence of knowing that the
robot will never let him approach the patient in a non-
desired area. However, while the surgeon does not
attempt to cross the shield, the reobot can be moved
freely.
4.2.2 Shield Generation
The problem here is to generate a surface that con-
nects the inner polygonal curve defined by the sur-
geon with an outer curve. The connection between
them is done in a smooth way, as Fig. 8 illustrates.
Figure 8: Lateral view of a face and the virtual shield.
The surface, s(u, v), is parametrized as the upper
part of a regular torus, but adapting its equators to the
inner and outer curves, as in (4).
Inn. curve i (t) = (i
x
(t) , i
y
(t)) t ∈ 0..2π(2)
Out. curve o (t) = (o
x
(t) , o
y
(t)) t ∈ 0..2π(3)
s(u, v) =
sin
2
v
2
i
x
(u) + cos
2
v
2
o
x
(u) ,
sin
2
v
2
i
y
(u) + cos
2
v
2
o
y
(u) ,
H sin (v)
u ∈ 0..2π v ∈ 0..π (4)
There are peculiarities of the shield to consider:
• The shield should be smooth, in order to make
navigation over it as comfortable as possible.
Once the surface is generated it is transformed
into a triangle model. By augmenting or decreas-
ing the number of triangles, one can vary the
smoothness of the surface.
• Reaching the inner curve from the surface it has
to be easy and intuitive. This implies certain re-
strictions on the shield design. This property de-
pends on the way inner points are connected to
outer points. First of all inner and outer curves
have to be parametrized, (2) and (3). There are
some restrictions regarding them in order to make
the surface easy and intuitive.
- i (t) and o (t), must be parametrized radially,
from an inner point, with constant radial veloc-
ity, in order to avoid self intersections of the
surface, as in Fig. 9 a) and b).
- The polygon defined by i (t), must be star-
shaped from the parametrization origin, in or-
der to avoid self intersections of the surface, as
in Fig. 9 c) and d).
- If i (t) defines a non star-shaped polygon a pre-
vious step must be done. An adaptation disc be-
tween the polygon and its convex hull is needed
before constructing the shield, so that the latter
can be parametrized radially from a suitable in-
ner point, as in Fig. 10.
Figure 9: a) Non valid parametrization of curves (self inter-
section of the surface). b) Valid parametrization of curves.
c) Non valid point for radial parametrization of curves.
Polygon is not star-shaped from that point. d) Valid point
for radial parametrization of curves.
Figure 10: Adaptation disc between an non star-shaped
polygon and its correspondent 2D Convex Hull.
• H, the height of the shield, must be chosen in or-
der to protect the patient.
Once the required smoothness for the surface is de-
fined, the parametrization for i (t) and o (t), solved
the problem with non star-shaped polygons and cho-
sen a desired height, the surface is generated by eq.
(4).
Finally, the intersections of the discrete set of
geodesics u =
2π
N
n and v =
π
N
n for n ∈ 1 . . . N is
triangulated in order to obtain the geometrical model.
The parameter N allows us to choose the number of
points and triangles of the surface, and ultimately its
smoothness.
RPQ: ROBOTIC PROXIMITY QUERIES - Development and Applications
65

4.2.3 Cutting Aid
Besides the shield generated, another virtual object is
proposed in order to aid the surgeon to carry out the
cut with great accuracy. It consists of an inner cover
that prevents the driller from escaping the perimeter
of the shape defined.
Since (2) has the shape of the cut to be done, we
define
b
i (t) as an under scaled version of i (t).
b
i (t)
has the same shape as i (t) but its sides are placed at
a distance ∆x from i (t) sides, being ∆x the desired
width for the cut.
Therefore, a new shield is generated, bs(u, v), hav-
ing a semisphere shape, with
b
i (t) as its equator,
parametrized by (5).
s(u, v) =
= H cos
2
(v) cos (u) + sin
2
(v)i
x
(u) sin (v),
H cos
2
(v) sin (u) + sin
2
(v)i
y
(u) sin (v),
H cos (v) u ∈ 0..2π v ∈ 0..
π
2
(5)
5 CONCLUSION
This paper presents the development of RPQ, a prox-
imity queries library optimized for applications where
robots share a common workspace and interact with
objects. Due to the amount of collision detection
packages, RPQ is built above a generic collision pack-
age, PQP. It is the generic collision package that better
fits RPQ purposes.
The goal of developing RPQ was to fill an exist-
ing gap in computer tools for robotic applications,
where robots interact with objects in their environ-
ment. Three optimizations have been performed to a
generic collision library: working with different reso-
lution levels of representation, the use of a weighted
matrix for choosing the best order for collision check-
ing and the definition of a binary matrix that deter-
mines the possibility of collision between objects.
RQP has been validated in different applications such
as multirobot collision avoidance, virtual robot con-
troller and surface navigation.
As expected, optimizations improve the time per-
formance of the system, although this improvement is
highly application dependent.
The introduction of different levels of resolution
in the geometric models of the objects and robots gen-
erally decreases the computational time for collision
checking. The use of bounding boxes decreases dras-
tically the number of high resolution queries needed.
This is a really important point taking into account
that they are much more time consuming. There are
cases where low resolution queries do not solve the
whole collision query. This increases the computation
time. However, choosing a suitable order for check-
ing collisions helps to find them in a quicker manner.
The precomputation of impossibilities of collision be-
tween different objects (Collision Matrix) increases
the performance of the system in case of having ob-
jects with restricted mobility in the workspace.
The combined use of optimizations generate good
results in workspaces shared by at least two robots
and objects.
RPQ has a wide range of applicability. RQP li-
brary is not only useful for proximity queries but has
also proved to be a good tool for surface navigation
and virtual representations, due to its ability to intro-
duce virtual objects in the shared workspace. The vir-
tual fixtures developed in the paper are examples of
how RPQ can be used to modify robot’s behaviour.
As proved in the application presented, RPQ is not
only useful for developers of robotic applications, but
also for users of robotic applications, i.e. surgeons
that require new robotic tools for improving surgical
procedures.
REFERENCES
Bergen, G. V. D. (2002). Solid collision detection library
users guide.
B.Geiger (2000). Real-time collision detection and re-
sponse for complex environments. In International
Conference on Computer Graphics. IEEE Computer
Society.
Giralt, X. and Hernansanz, A. (2006). Optimization of
proximity queries in robotic environments. In AVR
- 2es Jornades UPC de Recerca en Automtica, Visio i
Robotica (in catalan).
Kim, Y., Lin, M., and Manocha, D. (2002). Deep: Dual-
space expansion for estimating penetration depth be-
tween convex polytopes. In International Conference
on Robotics and Automation. IEEE.
S.Ehmann and Lin, M. (2000). Accelerated proxim-
ity queries between convex polyhedra by multilevel
voronoi marching. Technical report, Department of
Computer Science, University of North Carolina.
S.Ehmann and Lin, M. (2001). Accurate and fast proximity
queries between polyhedra using convex surface de-
composition. In Eurographics, volume 3.
Stanisic, Z., Jackson, E., and Payandeh, S. (1996). Virtual
fixtures as an aid for teleoperation. In 9th Canadian
Aeronautics and Space Institute Conference.
UNC (1999). Pqp - a proximity query package by research
group on modeling, physically-based simulation and
applications.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
66
