GPC BASED ON OPERATING POINT DEPENDENT
PARAMETERS LINEAR MODEL FOR THERMAL PROCESS
Riad Riadi, Rousseau Tawegoum, Gérard Chasseriaux
*
Unité de Sciences Agronomiques appliquées à l’Horticulture SAGAH A_462, INH-INRA-UA
Institut National d’Horticulture, 2, rue Le Nôtre 49045 Angers, France
Ahmed Rachid
Université de Picardie Jules Verne. IUP GEII. 33 rue Saint LEU 80000 Amiens, France
Keywords: HVAC system, non linear system, generalized predictive control, operating point dependent parameters
model, temperature control.
Abstract: This paper presents the application of generalized predictive control strategy (GPC) based on an OPDPLM
(Operating Point Dependent Parameters Linear Model) structure to a heating and ventilation nonlinear-
subsystem of a complex passive air-conditioning unit. For this purpose, several discrete-time models were
identified with respect to measurable exogenous events. The parameters of the identified models change
according operating conditions (sliding opening window). The objective of the studied subsystem was to
guarantee a microclimate with controlled temperature set-points. The on line adaptive strategy was
implemented to compute the controller parameters in order to adapt to the operating conditions variations.
Efficiency of the resulting algorithm is illustrated by a real experiment.
1 INTRODUCTION
The consumption of energy by Heating, Ventilating,
and Air Conditioning (HVAC) equipments in
industrial and commercial buildings constitutes 50%
of the world energy consumption (Arguello-Serrano
and Vélez-Reyes 1999). Growing crop in
greenhouse is one of important branch of agriculture
industry and, it is labour intensive and technically
challenging business. Optimized control helps to
increase production despite saving precious sources
(Young and Lees 1994). Standard air-conditioning
units which are used in environment control for the
growth chambers are usually composed of heating
elements, a cooling system with compressor and
evaporator techniques (Albright 2001), (Jones et al.,
1984), (Hanan 1997). The air-conditioning unit
studied is passive and does not use the more typical
compression system or absorption-refrigeration
cycle (Tawegoum et al., 2006a, Riadi et al., 2006).
The specificity of the system is to produce a variable
microclimate with variable temperatures and
variable relative humidity set-point values.
A complete physical model of this plant
developed in (Riadi et al., 2006), showed that the
global system is complex and composed of three
HVAC nonlinear subsystems. Therefore the
implementation of centralized control strategy is
cumbersome and decreases reliability. For these
reasons, a typical local-loop control configuration
for each subsystem of this air conditioning unit will
be more efficient. For such control loops, self tuning
controller parameters is usually considered, and the
present study is focused only on one single-input-
output (SISO) non linear subsystem, with multiple
operating modes. Many adaptive strategies using
recursive estimator are generally applied on thermal
process (Arguello-Serrano and Vélez-Reyes 1999),
(Landau and Dugard 1986), (Ljung 1999),
especially, efficient, when parameters values are
slowly varying. In our case, an idea about the model
structure is possible and the parametric disturbance
factor is measurable.
A generalized predictive control strategy, based on
online controller parameters adaptation, was used to
ensure stability and desired performances. Sub-
systems operating points were modeled by a linear
structures. These models should be fairly close in
their structure but with different parameters values.
The different models were identified for the main
302
Riadi R., Tawegoum R., Chasseriaux G. and Rachid A. (2007).
GPC BASED ON OPERATING POINT DEPENDENT PARAMETERS LINEAR MODEL FOR THERMAL PROCESS.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 302-307
DOI: 10.5220/0001629403020307
Copyright
c
 SciTePress

operating points and the outdoor disturbance
variations were taken into account and were
parameterized using polynomial function
interpolation in order to provide a single structure,
called Operating Point Dependent Parameters Linear
Model (OPDPLM) (Lakhdari et al., 1994), (Landau
et al. 1987).
This paper proceeds as follows. The problem
statement is presented in section II. In section III, the
process control problem in presence of multiple
operating modes is formulated and the proposed
GPC (Generalized Predictive Control) based on
OPDPLM is presented.The last section shows the
real-time implementation and the experimental
results are discussed.
2 SYSTEM DESCRIPTION AND
PROBLEM STATEMENT
Figure 1 outlines the overall design of the proposed
air-conditioning unit. The main features of the unit
are: a humid climate, operation without a freezing
unit, equilibrium of head losses and minimum
energy consumption. Moisture removal is not
required.
The unit is composed of two flows: a non-
saturated flow (or non-saturated duct) and a
saturated flow (saturated duct). As shown in Figure
1, in the saturated air flow, fresh air is saturated on
with water after being heated by a coil resistor.
Saturation operates at constant enthalpy (Chraibi et
al., 1997). The saturated duct subsystem consists of
a closed system, including a suction pump, a water
tank and cross-corrugated cellulosic pads of the type
using in cooling. The suction pump carries water
from the tank to the top of the pads. Once the
saturation steady state is reached, the pads contain a
constant mass of water with a given water output
and a given temperature.
In the unsaturated duct subsystem, fresh air is
only heated by another resistor coil to a desired
temperature
The proportional mixing of the two air flows is
carried out by a sliding window driven by a DC
motor.
Figure 1: Complete air-conditioning system.
In this paper, we are interested in the unsaturated
duct subsystem. The purpose control strategy is to
regulate the temperature
()
tT
ODD
(°C) of the
outgoing air at constant temperature reference
r
T
(°C), in spite of air flows variations through the
unsaturated duct and in spite of air intake
temperature behaviour
akeair
T
int_
(°C). The air flow
varied by changing the sliding window
percentage,
x
(%). This latter is close to air flow by
Eq(1).
(
)
Vair
Qxq .
1
α
=
(1)
The heat balance in the unsaturated duct is given
by the following equation:
[]
DD
DDairair
RDD
ODDakeair
DD
air
V
ODD
U
VC
k
TT
V
Qx
dt
dT
ρ
α
+
−=
int_
)(
(2)
with
DD
U the applied voltage (V), proportional
to the resistor heating in the dry duct,
RDD
k the
proportional coefficient between the voltage and the
heating-power (J/sV),
DD
V the volume of the dry
duct (m
3
).
GPC BASED ON OPERATING POINT DEPENDENT PARAMETERS LINEAR MODEL FOR THERMAL PROCESS
303

3 GENERALIZED PREDICTIVE
CONTROL OF NONLINEAR
CLASS SYSTEM
3.1 The Operating Point Dependent
Parameters-linear Model
The existence of a system with parameters
depending on the operating point (the particular case
of affine systems) means that one or more
parameters of a linear differential equation vary
according to an auxiliary variable
ζ
, which
represents the operating point (Landau et al., 1987).
An application to the temperature identification of a
helium bath cryostat is presented in (Lakhdari et al.,
1994), and it is also used in (Tawegoum et al.,
2006b) for climate identification nearly steady
weather conditions. This variable can be calculated
via the input or output process, or via another
measurable variable related to the operating point.
The Operating Dependent Parameter Linear Model
(OPDPLM) has the following properties:
- It allows the description of the non-linear
phenomena with regard to the operating point
ζ
.
- It makes it possible to extend the linear
formalism to systems that are not linear.
The system input-output form given by “(3), (4),
and (5)” is as follows:
)().,),((.)().,),((
11
tUqdtBqtYqdtA
d
Δ=Δ
−−−
ζζ
(3)
),),((
1−
qdtA ζ
is polynomial in
1−
q
, depending on
the delay d, nonlinear with respect to
)(t
ζ
, and
defined by:
i
na
i
i
qidtaqdtA
−
=
−
∑
−−+= .))((1),),((
1
1
ζζ (4)
The polynomial
)),((
1−
qtB ζ is non-linear in )(t
ζ
,
polynomial in
1−
q , and is defined by
i
nb
i
qit
i
bqtB
−
=
−
∑
−= .))(()),((
0
1
ζζ (5)
na, nb are respectively the polynomial degrees of
),),((
1−
qdtA ζ and of )),((
1−
qtB ζ , issued from
the identification process.
The parameters
))(( t
i
a
ζ
and ))(( t
i
b
ζ
can be
modeled by polynomial functions of order
1
η
and
2
η
as follows:
∑
=
=
1
0
)())((
η
ζζ
j
iji
t
j
ata (6)
∑
=
=
1
0
)())((
η
ζζ
j
iji
t
j
btb (7)
In our case, the percentage of the window
opening represents the operating point (
x=
ζ
).
3.2 GPC Design based on OPDPLM
The basic idea of the GPC (Clarke et al., 1987 a),
(Clarke et al., 1987 b), (Camacho and Bordons
1998) is to calculate a sequence of future control
signals is such way that it minimizes a multistage
cost function defined over a control horizon. The
index to be optimized is normally the expectation of
a function measuring the distance between the
predicted system output and some predicted
references sequence over the control horizon plus a
function measuring the control effort on the same
horizon.
Consider the plant described by CARIMA
(Controlled Auto-Regressive Integrated Moving
Average) model in OPDPLM case:
(
)
()
(
)
()
()
(
)
()
1
111
,1,,,
−
−−−
Δ
+−=
q
t
qCtuqdBtyqA
ε
ζζζ
(8)
The optimal j-step predictor defined between
1
N and
2
N is given by:
()
(
)
()
()
()
() ()
1,
1,,
1
11
−+Δ
+−Δ+=+
−
−−
∧
jtuqG
tuqHtyqFjty
j
jj
ζ
ζζ
(9)
Where polynomials
jjj
HGF ,,
are solutions of
the following Diophantine equations:
(
)
(
)
(
)
(
)
1,,,
1111
=+Δ
−−−−−
qFqqJqAq
j
j
j
ζζζ
(10)
(
)
(
)
(
)
(
)
1111
,,,,
−−−−−
=+ qJqBqHqqG
jj
j
ζζζζ
(11)
The cost function is given by
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
304

()()()() []
() []
⎪
⎭
⎪
⎬
⎫
−+Δ
⎪
⎩
⎪
⎨
⎧
++−+=
∑
∑
=
=
u
N
Nj
N
Nj
u
jtu
jtwjtyENNNJ
1
2
1
2
2
21
1
,,,
λ
λ
(12)
with
1
N the minimum prediction horizon;
2
N
the maximum prediction horizon,
u
N the control
costing horizon and
λ
a control-weighting.
Minimizing the cost function yields the control
law
()() () ()( )
1
1
,,, YWdGIdGdGU
TT
opt
−⋅+⋅=Δ
−
ζλζζ
(13)
The previous equation can be written as:
()( )
1
, YWdMU
opt
−⋅=Δ ζ
(14)
Where
()() () ()
dGIdGdGM
TT
,,,
1
ζλζζ
−
+⋅= (15)
With
G a
()
u
NNN ×+− 1
12
matrix.
Its elements are the coefficients of step response
depending on the operating point.
()( )() []
T
NtwNtwNtwW
211
,,1, ++++= " is the
reference signal within the prediction horizon;
()( ) () []
T
NtyNtyNtyY
2111111
,,1, ++++= " is the
prediction based on the past measurements.
Notice that
UΔ is not a scalar but a vector which
can be written as:
() ( ) ( ) []
T
uopt
optopt
opt
NtututuU +Δ+ΔΔ=Δ "1
(17)
In real time control, only the first value of Eq (14) is
finally applied to the system, according to the
receding horizon strategy.
()( )
11
, YWdmu
opt
−
⋅=Δ
ζ
(16)
With
()
dm ,
1
ζ
is the first line of the matrix M
The RST polynomial controller structure given
by (Dumur et al., 1997) can be extended for
OPDPLM formalism (figure. 2) as:
(
)
(
)
(
)
(
)
() ( )
(
) twqTtyqRtuqqS ,,,
111
ζζζ +−=Δ
−−−
. (18)
With,
(
)
(
)
(
)
11
1
1
,1,
−−−
+= qqHmqS ζζζ (19)
(
)
(
)
(
)
1
1
1
,,
−−
= qFmqR ζζζ
(20)
(
)
(
)
[
]
21
1
....,
NN
qqmqT ζζ = (21)
Where
(
)
(
)
[
]
T
NN
qFqFF
1
2
1
1
,,
−−
= ζζ "
(22)
(
)
(
)
[
]
T
NN
qHqHH
1
2
1
1
,,
−−
= ζζ " (23)
The adapting phase of regulator parameters can be
performed according stability and robustness, by
considering the updating the controller parameters
as:
1
1
=
N , and
(
)()()
(
)
ζζζλ GGtrace
T
opt
⋅= .
The closed loop stability using the equivalent RST
controller structure was studied in (Dumur et al,
1997), (M’saad and Chebassier.)
4 EXPERIMENTAL RESULTS
A set of electronic units was used to apply heating
voltage on the resistors or to control the DC motor
and thus, the window opening rate. Measurements
were carried out using Pt100 sensors for
temperature, and encoder sensors for position
window. A sampling interval of Te=30 sec was
chosen to satisfy the predominant time constant, and
data acquisition time varied from two to four hours,
depending on the operating point values
]
[
%100%,0
∈
=
x
ζ
for a large interval variation .
4.1 Discrete Model Identification for
Different Operating Modes
The air-flow measurements for the main window
positions indicate a nonlinear relationship between
the air-flow percentage and the window opening
percentage (Tawegoum et al., 2006c). Therefore, in
the identification process, the parameters of the
model describing the output temperature behavior of
the conditioning unit were assessed using the ARX
model for each window position (i.e. for each
operating point). A linear difference equation of the
type of structure case is given in (Landau et al.,
1987):
GPC BASED ON OPERATING POINT DEPENDENT PARAMETERS LINEAR MODEL FOR THERMAL PROCESS
305

∑∑∑
===
−−=−+
nj
i
jssjsi
m
s
nj
i
MjjiMj
rikUxbikYxakY
111
)()()()()(
(24)
The choice of ARX structures was based on their
advantageous application in digital models, i.e. use
of simpler and effective estimation algorithms and
because of their easy and flexible usage in computer
software (Borne et al., 1990).
The ARX model obtained for the temperature
model, in the non-saturated flow, is given in (Riadi
et al., 2006):
)()(2
.)(1)().
2
)(2
1
)(11(
int_
1
1
teTqxb
UqxbtTqxaqxa
akeair
DDODD
++
=
−
+
−
+
−
−
(25)
where
)(xa
i
and )(xb
i
are four-degree polynomials,
depending on
x
, the window opening percentage:
x 11.0663- x30.6083 x34.3282- x13.6201 a1(x)
234
+=
x3.0954 x8.2317- x8.8203 x3.4418- a2(x)
234
++=
x 0.7962 x2.7780- x3.6847 x1.6383- b1(x)
234
++=
x 0.3385 x0.8865- x1.0765 x0.4537- b2(x)
234
++=
(26)
4.2 Results of Strategy Control
The control parameters were chosen as follows: the
minimum prediction horizon
1
1
=N , the maximum
prediction horizon
14
2
=N , the control costing
horizon
7=
u
N , and the control
weighting
() () ()
(
)
ζζζλ GGtrace
T
⋅= 93.0
.
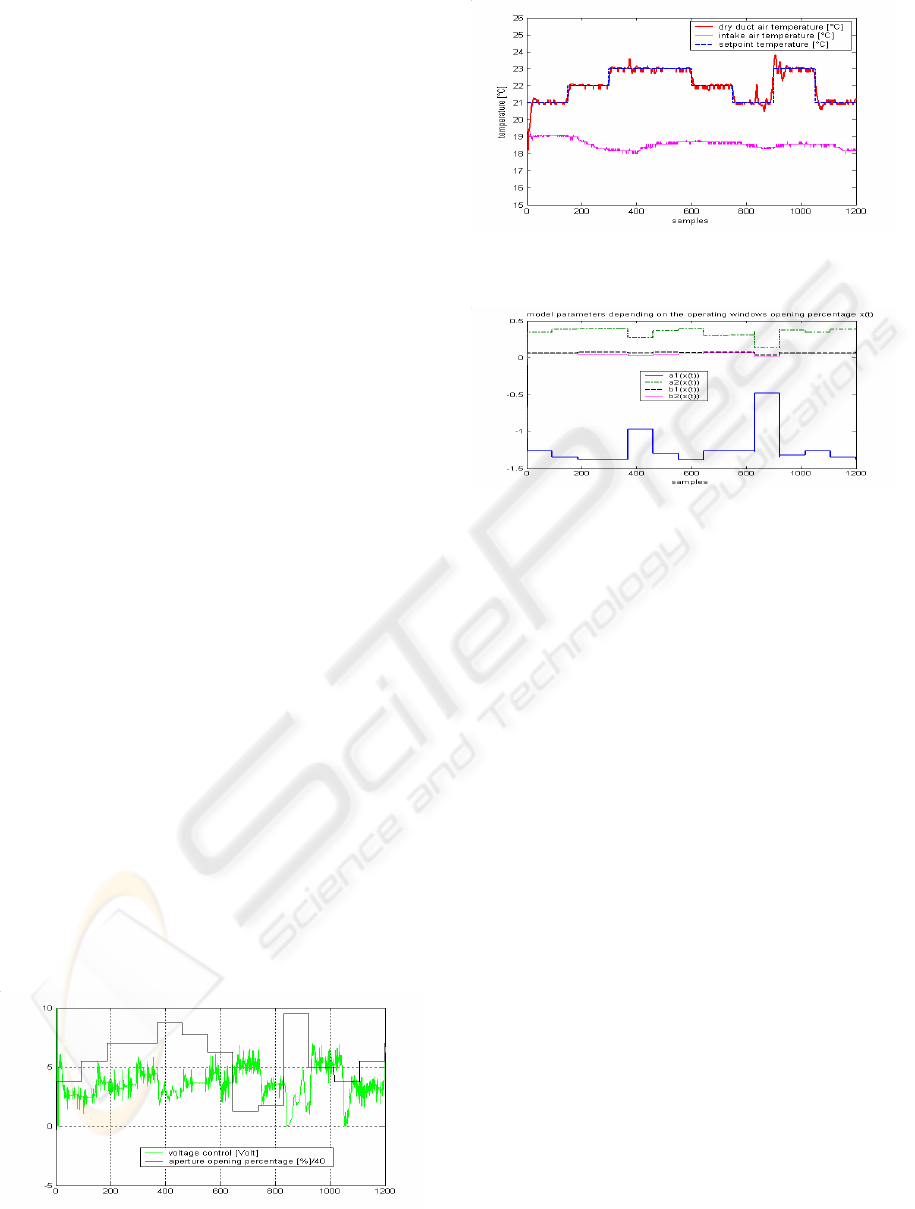
Figure 3 illustrates the temperature response over a
ten hours period, when applying the GPC strategy
based on the OPDPLM elaborated in (13), subject to
external temperature disturbances and to parameters
disturbances by varying the window opening.
Figure 2: The window opening rate and voltage control.
Figure 3: Regulation of temperature of non saturated using
GPC based on OPDPLM.
Figure 4: Parameter evolution of the model system.
The objectives of stability and energy minimization
are reached (disturbances rejection and robustness
stability).
As it can be seen the temperatures reach their set-
points in a very short time, exhibiting a small
overshoot. It can also be observed that an interaction
exists between the variation of the aperture position
and the output temperature.
Figure.3 shows that, consecutive to the switching
parameters (window moving), oscillatory behavior
appears on the output temperature response, due to
the control input discontinuties. The GPC algorithm
shows robustness in spite of these disturbances.
5 CONCLUSION
This paper has presented an application of the
generalized predictive control using the OPDPLM
structure of nonlinear thermal process. Stability is
maintained with an adequate choosing of controller
parameters values. The performances are maintained
in spite of parameters system variation and
controller disturbance rejection is capable to reduce
the effect of thermal loads, with a simple updating of
the regulator parameters depending on operating
points.
The control strategies will be performed with an
introduction of an overshoot constraint on the output
temperature and with robust techniques of the GPC
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
306

algorithm.
Further investigations on the decentralized
architecture make it possible to extend this local
control strategy to other part of the complex air
conditioning unit.
REFERENCES
Albright, L.D, Gates, R.S, Aravantis, K.G, and Drysdale,
A.E. “Environment Control for Plants on Earth and
Space,” IEEE Control Systems Magazine, pp. 28-47,
October 2001.
Arguello-Serrano, B, Vélez-Reyes, M. “Non linear control
of heting, ventilating, and air conditioning system with
termal load estimation,” IEEE Tranactions on Control
Systems technology, vol. 7, No. 1, January. 1999, pp.
56–63.
Borne, P., Dauphin Tanguy, G., Richard., J.P., Rotella, F.,
Zambrettakis, I. “Modélisation et identification des
processus”. Techniques de l’ingénieur, Technip 1990.
Camacho, E.F and Bordons, C “Model predictive
Control’’ Springer edition, 1998.
Chassériaux, G., Tawegoum , R., and Lelièvre, M.
“Thermal simulation of an air conditioning unit based
on a heating system and humid corrugated pad.” 20
th
International Congress of Refrigeration” – Sidney
(Australia)– sept. Paper code 720, 1990.
Chraibi, A., Makhlouf, S. and Jaffrin, A. “Refroidissement
évaporatif de l'air des serres ”, Journal de Physique,
n°III. Juillet 1995. Dumur,D., Boucher,P., Murphy,
K.M., Déqué, F. ‘‘ On Predictive Controller Design
for Confort Control in Single Residential Housing’’.
ECC’97, juillet 1997.
Clarke, D.W., Mohtadi, C., and Tuffs, P.S., ‘‘Generalized
Predictive Control. Part I. The Basic Algorithm.’’
Automatica, 23(2):137-148, 1987.
Clarke, D.W., Mohtadi, C., and Tuffs, P.S., ‘‘Generalized
Predictive Control. Part II. Extensions and
interpretations’’ Automatica, 23(2):149-160, 1987.
Dan Van Mien, H., and Normad-Cyrot, D. “Non linear
state affine identification methods, application to
electrical power plant”, Automatica, Vol 20, pp. 175-
188, 1984.
Dumur.D,P. Boucher, K.M. Murphy, F. Déqué “On
predictive controller design for comfort control in
single residential housing”, ECC’97-juillet 1997.
Hanan, J.J. “Greenhouse: advanced technology for
protected horticulture.”, Chapter 4, pp. 236-260, 1997.
Hansen, J.M., and , Hogh Schmidt, K., “A computer
controlled chamber system design for greenhouse
microclimatic modelling and control. ” Proc. Int.
Sym.on Plant Production in closed Ecosystems. Acta
Horticulturae, n°440, ISHS, pp. 105-110., 1996.
Jones, P., Jones., J.W., Allen, L.H. and Mishve J.W.
“Dynamic computer control of closed environmental
plant growth chambers, ” Design and Verification.
Transaction of ASAE. (American Society of
Agricultural Engineers), pp. 879-888, 1984.
Lakhdari, Z., Lécluse, Y. and Provost, J., “Dynamic
control of a system with operating point dependent
parameters, application to cryogenic.” In Proc of the
international AMSE conference, Sytems Analysis,
Control & Design, SYS'94, Lyon (France), July, vol.
2, pp. 243 -253. ISBN : 2-909214 -57-5, 1994.
Landau, I.D., Dugard, L. “Commande adaptative aspect
pratiques et théoriques,” , J. Masson, Ed. Paris , 1986,
pp. 1–81.
Landau, I. D., Normand-Cyrot, B., and Montano, A.
“Adaptive control of a class of nonlinear discrete time
systems: application to a heat exchanger,” in Proc.
28
th
Conference on Decision and Control, Los
Angeles, Ca December 1987, pp. 1990-1995.
Ljung, L. “System identification”, Theory for the user,
Prentice Hall, 1999.
M’ssad, M., Chebassier, J. “Commande adaptative des
systèmes,” Techniques de l’ingénieur, vol. 7426, pp.
1–25.
Nybrant, T.G. “Modelling and adaptive control of
concurrent flow driers, ” Computers and Electronics
in Agriculture, 1989, 3, 243-253.
Ramond,G., Dumur, D., Libaux, A., Boucher, P.,‘‘ Direct
adaptive predictive control of an hydro-electric
plant’’, Proceedings 10
th
, Conference on Control
Apllications, pp. 606-611,Mexico,Septembre 2001.
Riadi, R., Tawegoum., R., Rachid, A, Chassériaux, G.
‘‘Modeling and Identification of a Passive Air-
Conditioning Unit using the Operating Dependent
Parameters-Structure’’. Presented CESA-2006:
Computational Engineering in Systems Application,
Beijing, Chine, 4-6 Octobre 2006.
Tawegoum, R., Teixeira, R. and Chassériax., G.
“Simulation of humidity control and temperature
tracking in a growth chamber using a passive air
conditioning unit,” Contol Engineering Practice
Journal, 2006a, 14/8, 853-861.
Tawegoum R., Lecointre B., “A linear parametric model
of an air conditioning unit with operating point
dependent parameters under nearly steady weather
conditions,” 5 th Vienna Symposium on Mathematical
Modelling, Vienna-Austria, February 2006b, Mech,
3.1-3.8.
Tawegoum,, R., Bournet, P.E, Arnould, J., Riadi R., and
Chassériax., G. “Numerical investigation of an air
conditioning unit to manage inside greenhouse air
temperature and relative humidity,” International
Symposium on Greenhouse Cooling, Almeria-Spain,
April 2006c.
Young, P.C. and Lees, M.J. “Simplicity out of complexity
in glasshouse climate modeling, ” in Proc. 2
nd
IFAC/ISHS Workshop on Mathematical an Control
Application in agriculture and Horticulture, 12-15
september 1994, Silsoe, United kingdom, Acta
Horticuturae N°406, pp.15-28.
GPC BASED ON OPERATING POINT DEPENDENT PARAMETERS LINEAR MODEL FOR THERMAL PROCESS
307