A JOINT HIERARCHICAL FUZZY-MULTIAGENT MODEL

DEALING WITH ROUTE CHOICE PROBLEM

RoSFuzMAS

Habib M. Kammoun, Ilhem Kallel and Adel M. Alimi

Research Group on Intelligent Machines REGIM, University of Sfax, Tunisia

Keywords: Transportation Route Choice problem, Intelligent Transportation System, MultiAgent System, Fuzzy

Controller.

Abstract: Nowadays, multiagent architectures and traffic simulation agent-based are the most promising strategies for

intelligent transportation systems. This paper presents a road supervision model based on fuzzy-multiagent

system and simulation, called RoSFuzMAS. Thanks to agentification of all components of the transportation

system, dynamic agents interact to provide real time information and a preliminary choice of advised routes.

To ensure the model rationality, and to improve the route choice make decision, we propose to use a

hierarchical Fuzzy inference including some pertinent criteria handling the environment as well as the driver

behavior. A multiagent simulator with graphic interface has been achieved to visualize, test and discuss our

road supervision system. Experimental results demonstrate the capability of RoSFuzMAS to perform a

dynamic path choice minimizing traffic jam occurrences by combining multiagent technology and real time

fuzzy behaviors.

1 INTRODUCTION

In view of the enormous increase of vehicle number,

accidents and traffic jam situations become

widespread in all road networks in the world. A

solution for these problems is to develop and invest

in Intelligent Transportation System (ITS) which is

capable of managing in a better way the existing

capacity and encouraging more efficient vehicle

routing over time and space, in order to improve

safety, traffic efficiency, etc. Varied applications of

ITS currently under development represent a real

opportunity to advance toward a best future.

Furthermore, a number of ITS based on

multiagent approach came recently into being to

improve performances dynamic routing and traffic

management by employing collaborative driving

system (Hallé and Chaib-Draa, 2005) or by route

guidance system (Adler et al. 2005).

Since the nineties, the use of fuzzy logic in ITS is

marked. Research in soft computing field has been

exploring the application of fuzzy set theory as a

framework solving many transportation problems

(Teodorovic, 1999), as route choice problem, traffic

assignment problem, traffic control at the

intersection, accident analysis and prevention, and

traffic light controller. The majority of authors are

based on a comparison of fuzzy values representing

the routes’ costs. The corresponding rules are of the

type: “If times on route 1 and 2 are very high, I will

probably take route 3”.

In this sense, this paper presents a joint

hierarchical fuzzy-multiagent model dealing with

transportation route choice problem. Our model

called RoSFuzMAS, acronym for “Road Supervision

based on Fuzzy MultiAgent System” is poised

between two different philosophies: the distributed

and parallel ITS and the uncertain reasoning. To

ensure the model rationality, and to improve the

route choice make decision, we propose to use a

hierarchical Fuzzy inference including some

pertinent criteria handling the environment as well

as the driver behavior.

The paper is organized as follows: Next section

presents our road supervision system. The third

section describes the improvement of decision

making for route choice problem by adding other

decision criteria structured in a hierarchical fuzzy

controller. The simulation part detailed in the forth

section gives an idea about the environment and

discusses some results.

394

M. Kammoun H., Kallel I. and M. Alimi A. (2007).

A JOINT HIERARCHICAL FUZZY-MULTIAGENT MODEL DEALING WITH ROUTE CHOICE PROBLEM - RoSFuzMAS.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 394-397

DOI: 10.5220/0001629503940397

 SciTePress

2 A ROAD SUPERVISION

DISTRIBUTED UNDER

MULTIAGENT APPROACH

Since some years ago, multiagent systems (MAS)

took hold data processing (Wooldridge, 2002).

Indeed, a cooperative interaction always leads to an

increase of quantitative and qualitative system

performances (Kallel et al., 2002), (Kammoun et al.,

2005), (Kallel and Alimi, 2006).

In this sense, our system has as objectives to

ensure an efficient network capacity allocation and

decrease the number of congestion situations.

Accordingly, the system proposes a best road choice

to help drivers’ vehicle to attempt their destinations.

We propose a model involving three kinds of

agents: City Agent (CA), Road Supervisor Agent

(RSA) and Intelligent Vehicle Agent (IVA). Figure 1

presents three levels of the proposed system as well

as the acquaintance links between CA, RSA and IVA.

Each agent use the organizational model AGRE

(Agent-Group-Role-Environment) (Ferber et al.,

2005) and lives according to a cycle bound to an

iterative process of reception / deliberation / action

detailed in (Kallel et al., 2006).

….

Hierarchical

level of groups

RSA

IVA

Interaction link

….

Figure 1: Hierarchical organizational architecture.

The RSA computes the traffic index for road i

(RFI

) according to equation (1).

max max

with Average ( )

vtvt

RFI

NTNT

∑

(1)

with N

is the number of vehicles in road i, N

vmax

is the maximum number of vehicles in this road, T

represents the time in jam state for vehicle j

calculating in T

period.

Equation 2 presents the Path Flux Index (PFI) as

a sum of RFI

average with the route length

pondered by a coefficient α.

PFI RFI l

∑

(2)

with nb is the number of road in the path, l

is the

length of road i and α is the length importance

coefficient.

3 HIERARCHICAL FUZZY

ROUTE CHOICE CONTROL

Modelling route choice behaviour is a complex

activity if we add other inputs. We try to improve

our route choice model by using fuzzy logic (Zadeh,

1965). Furthermore, the use of hierarchical fuzzy

controller in several applications’ areas showed a

real improvement in precision and interpretability

(Alimi, 1997), (Kallel et al., 2005) especially in

multi-choice problem.

As shown in figure 2, we select only the k first paths

as k alternatives for fuzzy choice, while fuzzifying

their PFI values. The hierarchical controller uses

other inputs fuzzy representations of route

characteristic depending on n criteria. It provides the

recommended route R to follow by the vehicle

driver.

Figure 2: Hierarchical fuzzy route choice model.

with FiPj is the fuzzy representation of path j corresponding

for criteria i and R is the

recommended route.

3.1 Fuzzy Criteria Controller FCC

Let suppose that k=3 and n=5, we will compare 3

alternative routes depending on 5 factors in urban

environment. These factors are the most important

FCC

FPFI

Arithmetic selection

FRCC

A JOINT HIERARCHICAL FUZZY-MULTIAGENT MODEL DEALING WITH ROUTE CHOICE PROBLEM -

RoSFuzMAS

395

criteria, more used, and accessible from the vehicle

information system.

The FCC allows a better road evaluation

according to criteria concerning the vehicle state, the

driver behavior and the environment.

 Inputs parameters: these criteria are presented

in descending order of their importance for

route choice makes decision.

o RWInformation (road work information, the

highest important criteria): NoRoadWork,

RoadWork

o TimeOfDay: Morning, Midday, Evening, Night

o Familiarity: Unfamiliar (with a route), Medium,

Familiar. This parameter takes in account the

driver’s experiences and will be updated in

each trip

o WeatherConditions: Bad, Medium, Good

o Speed: Slow, Medium, High

 Output parameters:

o Preference: Weak, Strong

The figure 3 draws the membership function

used in this case.

Figure 3: Fuzzification of inputs and output used in FCC.

 Rule base of FCC model: The rule base of

FCC model is built by combination of input and

output variables. This base is generated by experts in

the transportation area and formed initially by 216

rules. As an example of rule, we can cite: “if

RWInformation is NoRoadWork and TimeOfDay is

Night and Familiarity is Familiar and

WeatherConditions is Good and Speed is Medium

then Preference is Strong”.

 Fuzzy Inference and defuzzification of the

FCC model: For the inference process, Mamdani

(max–min) inference method is used in FCC model.

The Center of Gravity (COG) method is used for

defuzzification of the FCC model.

In view of the fact that the number of rules is high,

we propose to model this controller by a hierarchical

fuzzy architecture in order to gain in interpretability

without decreasing efficiency. We regroup by pairs

the criteria having some correlation.

3.2 Fuzzy Route Choice Controller FRCC

The FRCC uses as inputs, the outputs of FCC and a

Fuzzy representation the PFI, called FPFI.

 Input parameters:

o Preference: Weak, Strong

o FPFI: Low, Middle, High

 Output parameters:

o FP: VeryUnrecommended, Unrecommended,

Undecided, Recommended, VeryRecommended

 Rule base of FRCC model: The rule-base is

formed initially by 216 rules. As an example of rule,

we can cite: “if Preference is Strong and FPFI is

Low then FP is VeryRecommended”.

4 SIMULATION EXPERIMENTS

Figure 4 presents some virtual maps, created by

agent observer of TurtleKit tool (Michel et al.,

2005), in order to apply several tests varying

vehicles’ positions, environment conditions and

drivers’ behaviour factors.

Figure 4: Examples of simulation environments.

The simulator recognizes three kinds of vehicles

named classic vehicle, bad vehicle, and intelligent

vehicle. The first one is a vehicle without intelligent

module; the second one is a vehicle stopped in jam

situation; the third one is intelligent, that means it is

a part of RoSFuzMAS. With several tests, we try to

compare intelligent vehicle route choice behaviour

with a classic vehicle leaving from the same position

in the same time and having the same destination.

The first road network presented is a virtual map

holding eleven roads numbered from 1 to 11 in only

one city, and a variable number of cars circulating

with random and autonomous way. The network

state in defined time intervals is known as well as

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

396

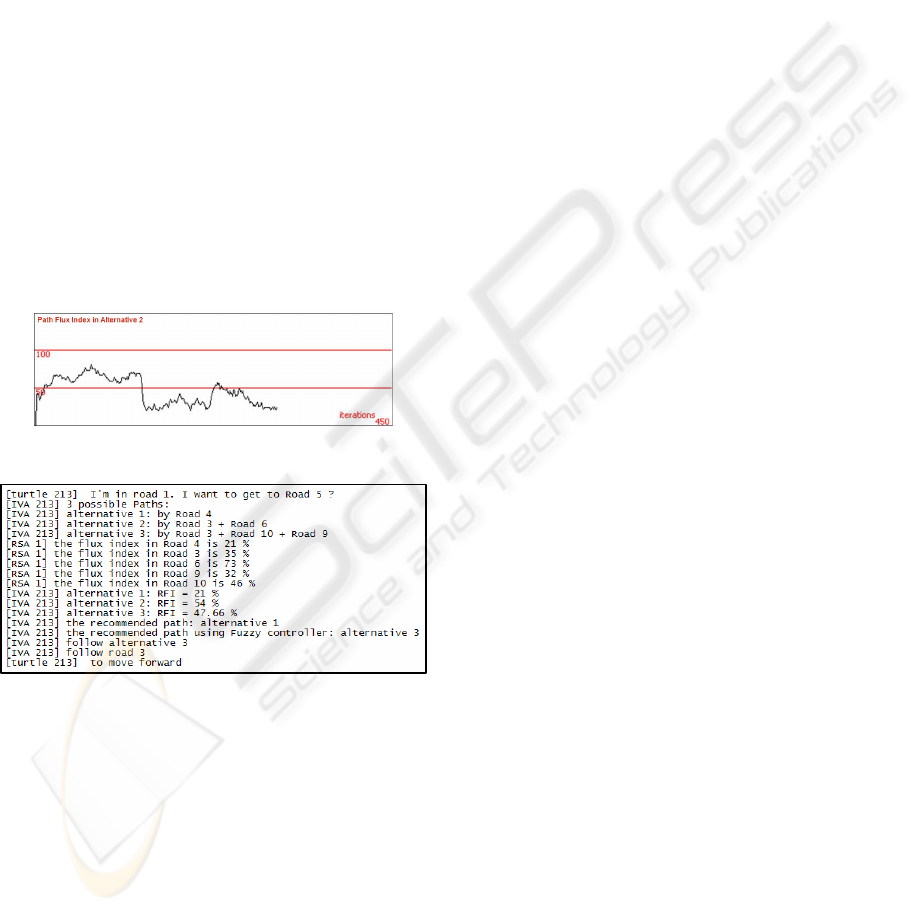
the traffic load intensity to be forwarded from road 1

to road 5. Figure 5 shows the road flux index in the

different alternatives from road number 1 to road

number 5. The IVA chooses the first alternative (by

road 4) because it has the smallest flux index

compared with second and third alternatives. The

flux index in the second alternative is high because

of jam situation in road 6. The flux index in the third

alternative is high because of the route length. The

RFI was from 0 to 100 %. The simulation has been

done every 450 seconds when updating the road flux

index table after every 60 seconds.

Second series of simulations was performed

using the fuzzy rule base with the same parameters

of the first simulation. Figure 6 confirms that after

the work information, bad weather condition, and

driver’s unfamiliarity of the road 4, the controller

proposes the third alternative to follow.

Various other simulations are applied with other

maps, other positions of clutters, and different

criteria. The results show that the fuzzy logic

application for route choosing gives a better

management of road network in all cases.

Figure 5: Viewer of Path Traffic Index.

Figure 6: Example of communication messages between

IVA and RSA.

5 CONCLUSION

In this paper, we presented a hierarchical

architecture as well as a model and a simulation of

road supervision system based on joint fuzzy logic

and multiagent approach. The route choice algorithm

developed shows acceptable results, but it become

very complex if we add other criteria for route

choice make decision.

The originality of this model resides on:

 A hierarchical fuzzy controller in the

multi-route choice problem.

 Generic architecture, without limit for the

number of factors to use.

 A hierarchical multiagent architecture handling

fuzzy inference for the route choice problem.

As perspectives, we intend in the near future to

add other options such as the factor of variant speed

for IAV, an advancement treatment of crossroads, an

environment with double way, and the change lane

problem. Applying learning methods such as (Kallel

et al., 2006) become a necessity in order to reduce

rule numbers and adjust membership functions.

Furthermore, paths learning and multiobjective

optimization of vehicle path planning can be added.

REFERENCES

Adler, J. L., Satapathy, G., Manikonda, V., Bowles, B., &

Blue, V. J., 2005. A multi-agent approach to

cooperative traffic management and route guidance.

Transportation Research Part B, 39(4), 297-318.

Alimi, A. M., 1997. A neuro-fuzzy approach to recognize

Arabic handwritten characters. In Proc. of the I. C. on

Neural Networks, vol. 3, 1397-1400.

Ferber, J., Michel, F. & Baez, J., 2005. AGRE: Integrating

environments with organizations. In Proc. of E4MAS,

Lecture Notes in Artificial Intelligence, 3374, 48-56.

Hallé, S., Chaib-Draa, B., 2005. A collaborative driving

system based on multiagent modelling and simulations.

Transportation Research Part C, 13, 320-345.

Kallel, I., Jmaiel, M., & Alimi, A. M., 2002. A Multi-

Agent Approach for Genetic Algorithm

Implementation. In Proc. of IEEE SMC, Tunisia.

Kallel, I., Jelleli, T. & Alimi, A. M., 2005. Hierarchical

FLS Design Using Multi-Agent Genetic Approach. In

Proc. of GFS’2005, Granada, Spain, 142-147.

Kallel, I., Alimi, A. M., 2006. MAGAD-BFS: A Learning

Method for Beta Fuzzy Systems based on a Multi-Agent

Genetic Algorithm. I. J. of Soft Computing, 10(9), 757-772.

Kammoun, H. M., Kallel, I., Alimi, A. M., 2005.

RoSMAS²: Road Supervision based Multi-Agent

System Simulation. In Proc. of the I. C. on Machine

Intelligence ACIDCA-ICMI’2005, Tunisia, 203-210.

Michel, F., Beurier, G., & Ferber, J., 2005. The TurtleKit

Simulation Platform: Application to Complex

Systems. In Proc. of SITIS’05, 122-127.

Teodorovic, D., 1999. Fuzzy logic systems for

transportation engineering: the state of the art.

Transportation Research Part A, 33(5), 337-364.

Wooldridge, M., 2002. An introduction to multiagent

systems, John Wiley and Sons. February 2002.

Zadeh, L., 1965. Fuzzy sets, Information and Control 8,

338-353.

A JOINT HIERARCHICAL FUZZY-MULTIAGENT MODEL DEALING WITH ROUTE CHOICE PROBLEM -

RoSFuzMAS

397