A STATE ESTIMATOR FOR NONLINEAR STOCHASTIC SYSTEMS

BASED ON DIRAC MIXTURE APPROXIMATIONS

Oliver C. Schrempf and Uwe D. Hanebeck

Intelligent Sensor-Actuator-Systems Laboratory, Universit

at Karlsruhe (TH), Germany

Keywords:

Nonlinear Dynamic Systems, Stochastic Filter, Dirac Mixture.

Abstract:

This paper presents a ﬁlter approach for estimating the state o f nonlinear dynamic systems based on recursive

approximation of posterior densities by means of Dirac mixture functions. The ﬁlter consists of a prediction

step and a ﬁlter step. The approximation approach is based on a systematic minimization of a distance measure

and is hence optimal and deterministic. In contrast to non-deterministic methods we are able to determine

the optimal number of components in the Dirac mixture. A further beneﬁt of the proposed approach is the

consideration of measurements during the approximation process in order to avoid parameter degradation.

NOTATION

k time index

state variable

measurement variable

ˆy

actual measurement at time k

ˆx

point estimate at time k

(x) probability density function of x

(x) approximation of

(x)

k+1

) predicted density function

) ﬁltered density function

, ˆy

) Likelihood functon

δ(x) Dirac Delta function

H(x) Heaviside step function

G distance measure

η parameter vector

γ progression parameter

N (., m, σ) Gaussian density with mean m

and standard deviation σ

1 INTRODUCTION

In this paper, we present a novel stochastic ﬁlter for

nonlinear dynamic systems suffering from system as

well as measurement noise. The uncertainty in the

ﬁlter’s estimate caused by the noise is described by

means of probability density functions. The problem

that arises with the application of stochastic ﬁlters to

nonlinear systems is that the complexity of the den-

sity representation increases and the exact densities

cannot be calculated directly in general. Common

solutions to this problem in order to build practical

estimators can be devided into two classes. The ap-

proaches of the ﬁrst class approximate or modify the

system and measurement functions and apply a ﬁl-

ter. The idea of the second class is to approximate

the resulting density functions themselves in order to

calculate the ﬁlter steps in closed-form .

A common representative of the ﬁrst class is the

extended Kalman ﬁlter (EKF). It is based on lineariza-

tion of the system and measurement functions and ap-

plying a standard Kalman ﬁlter to this modiﬁed sys-

tem. This approach is applicable to systems with only

negligible nonlinearities and additive noise, but fails

in more general cases.

Another approach is to approximate the system to-

gether with its noise as a probabilistic model (Huber

and Hanebeck, 2007). The application of adequate

representations of the model like Gaussian mixtures

with axis-aligned components (Huber et al., 2006),

allows for efﬁcient implementation of the ﬁlter steps.

Filters approximating the density functions in-

stead of the system function can be divided into two

C. Schrempf O. and D. Hanebeck U. (2007).

A STATE ESTIMATOR FOR NONLINEAR STOCHASTIC SYSTEMS BASED ON DIRAC MIXTURE APPROXIMATIONS.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 54-61

DOI: 10.5220/0001629600540061

 SciTePress

main approaches found in the literature: i) sample-

based representations and ii) analytic density repre-

sentations.

Sample-based ﬁlters like the popular particle ﬁl-

ter (Doucet et al., 2000)(Doucet et al., 2001) apply

Monte Carlo methods for obtaining a sample repre-

sentation. Since these sample are usually produced by

a random number generator, the resulting estimate is

not deterministic. Furthermore, Markov Chain Monte

Carlo Methods (MCMC) are iterative algorithms that

are unsuited for recursive estimation, hence, impor-

tance sampling like in (Geweke, 1989) is often ap-

plied. The problem of sample degradation is usually

tackled by bootstrap methods (Gordon, 1993).

Other methods describe the probability density

functions by means of their moments. A popular

approach is the so called Unscented Kalman ﬁlter

(UKF) (Julier and Uhlmann, 1997) that uses the ﬁrst

moment and the second central moment for represent-

ing the densities. This allows for an efﬁcient calcula-

tion of the update but fails in representing highly com-

plex densities arising from nonlinear systems. Fur-

thermore, the assumption of jointly Gaussian dis-

tributed states and measurements is made, which is

not valid in general.

An approach that represents the densities by

means of Gaussian mixture densities is the so called

Gaussian sum ﬁlter (Alspach and Sorenson, 1972).

The Gaussian mixture representation allows for ap-

proximating arbitrary density functions, but ﬁnding

the appropriate parameters is a tough problem. A

more recent approach is the Progressive Bayes ﬁlter

(Hanebeck et al., 2003) which uses a distance mea-

sure for approximating the true densities. The key

idea in this approach is to transform the approxima-

tion problem into an optimization problem. This is a

major motivation for the approximation applied in the

approach presented here.

The ﬁlter method we propose here follows the idea

of approximating the density functions instead of the

system itself, but the approximation is performed in

a systematic manner. The general idea is to approx-

imate the continuous density function by means of a

Dirac mixture function that minimizes a certain dis-

tance measure to the true density. The approxima-

tion process itself is described in (Schrempf et al.,

2006a)(Schrempf et al., 2006b) and will therefore

only be discussed brieﬂy in this paper. We will focus

here on the complete ﬁlter consisting of approxima-

tion, prediction (Schrempf and Hanebeck, 2007) and

ﬁlter step.

Since we make use of a distance measure, we

are able to quantify the quality of our approximation.

Furthermore, it is possible to ﬁnd an optimal num-

ber of components required for sufﬁcient estimates.

Following this idea we will extend our optimization

method to a full estimation cycle by considering the

measurement as well.

The paper is organized as follows: We will give

a problem formulation in Section 2 followed by an

overview of the complete ﬁlter in Section 3. The

building blocks of the ﬁlter are described in Section 4

whereas Section 5 presents further optimization meth-

ods. Experimental results comparing the proposed

ﬁlter to state-of-the-art ﬁlters are given in Section 6

followed by conclusions in Section 7.

2 PROBLEM FORMULATION

We consider discrete-time nonlinear dynamic systems

according to

k+1

= a

, u

, w

)

producing measurements according to the nonlinear

function

= h

, v

) .

The state of the system that is not directly observable

in general is represented by x

. u

is a known input,

and y

is an observable output of the system. a

(·) is

a time-varying nonlinear mapping describing the sys-

tem’s dynamic behavior. w

represents both endoge-

nous and exogenous noise sources acting upon the

system and is described by means of a density func-

tion f

). h

(·) maps the system state to an output

value which suffers from noise v

which is modeled

by means of a density function f

Starting with an initial state x

, our goal is to

keep track of the system’s state over time while main-

taining a full continuous stochastic representation of

the uncertainty involved caused by the system and

measurement noise.

This corresponds to sequentially calculating the

state densities f

), k = 1, .. . , N, by means of a

prediction and a ﬁlter step where the system and

measurement functions are applied.

Exact computation of these densities, however, is

not feasible, as the complexity of the density increases

in every step. In addition, the resulting densities

cannot be calculated in an analytic form in general.

The aim of this work is to provide a density rep-

resentation that approximates the true density, in or-

der to allow for closed-form calculation of the pre-

diction step while maintaining a predeﬁned quality

of the approximation with respect to a given distance

measure.

A STATE ESTIMATOR FOR NONLINEAR STOCHASTIC SYSTEMS BASED ON DIRAC MIXTURE

APPROXIMATIONS

For reasons of brevity, we omit the input u

. We

further focus on additive noise, which results in the

system equation

k+1

= g

) + w

and a measurement equation

= h

) + v

In addition, the time index k is omitted in some cases

without notice.

3 FILTER OUTLINE

In this section, we will give a brief overview of the

recursive ﬁltering scheme depicted as a block dia-

gram in Figure 1. The left part of the ﬁgure shows

the nonlinear system suffering from additive noise as

described in Sec. 2. The right part shows the estima-

tor. The input of the estimator is a measurement ˆy

coming from the system. The output of the estimator

is a probability density function f

) from which a

point estimate ˆx

can be derived. The estimator itself

works recursively as can be seen from the loop in the

diagram. Each recursion consists of a prediction step,

an approximation step, and a ﬁlter step.

The prediction step receives a density f

) from

the previous ﬁlter step. This density is an approxima-

tion represented by means of a Dirac mixture allow-

ing for an analytically exact solution of the Bayesian

prediction integral with respect to this approximation.

The prediction yields a continuous mixture density

representation (e.g. a Gaussian mixture)

k+1

Details are given in Sec. 4.2.

The continuous mixture density

k+1

) re-

sulting from the prediction step serves as input

to the approximation step. The density is sys-

tematically approximated by means of a Dirac

mixture f

k+1

) minimizing a distance measure



k+1

), f

k+1

)



as described in Sec. 4.1.

The approximated density f

k+1

) is then fed to

the ﬁlter step, where it gets fused with the likelihood

function f

(x, ˆy). This step is described in detail in

Sec. 4.3.

4 FILTER COMPONENTS

4.1 Density Approximation

We will now introduce Dirac mixture functions and

explain how they can be interpreted as parametric

density functions. Subsequently, we brieﬂy describe

the systematic approximation scheme.

4.1.1 Dirac Mixture Density Representation

Dirac mixtures are a sum of weighted Dirac delta

functions according to

f (x, η) =

∑

i=1

δ(x − x

) , (1)

where

η = [x

, x

, . . . , x

, w

, . . . , w

]

is a parameter vector consisting of locations x

, i =

1, . . . , L and weighting coefﬁcients w

, i = 1, . . . , L.

The Dirac delta function is an impulse representation

with the properties

δ(x) =



0, x 6= 0

not deﬁned, x = 0

and

δ(x) dx = 1 .

This results in the fundamental property

∞

−∞

f (x)δ(x − x

) dx = f (x

) .

A mixture of Dirac delta functions as given in (1) can

be used for representing arbitrary density functions

if the following requirements are considered. Since

the properties of a density function f (x) demand that

f (x) ≥ 0 and

f (x) dx = 1, we have

≥ 0, i = 1, . . . , L

and

∑

i=1

= 1 .

Hence, we require 2L parameters with 2L − 1 degrees

of freedom.

A simpliﬁed density representation is given by

equally weighted Dirac mixtures, as

f (x, η) =

∑

i=1

δ(x − x

) ,

where only L parameters and L degrees of freedom

are used. This results in a simpler, less memory

consuming representation with less approximation

capabilities.

Dirac mixtures are a generic density representa-

tion useful for approximating complicated densities

arising in estimators for nonlinear dynamic systems.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

Figure 1: A block diagram of the recursive estimator. The estimator consists of a ﬁlter step, a prediction step and an

approximation step.

4.1.2 Approximation Approach

A systematic approximation of continuous density by

means of another density requires a distance measure

between the two densities



k+1

), f

k+1

, η)



where

(·) is an arbitrary continuous density func-

tion and f

(·, η) is a Dirac mixture density. The ap-

proximation problem can then be reformulated as an

optimization problem by ﬁnding a parameter vector η

that minimizes this distance measure.

Popular distance measures for comparing contin-

uous densities, measures are the Kullback–Leibler di-

vergence (Kullback and Leibler, 1951) or the integral

quadratic measure. For comparing a continuous den-

sity to a Dirac mixture, however, they are not very

useful, since the Dirac mixture is zero between the

Dirac pulses. Hence, instead of comparing the den-

sities directly, the corresponding (cumulative) distri-

bution functions are employed for that purpose. For

the rest of this subsection we will omit the time in-

dex k and the p index in order to keep the formulae

comprehensible.

The distribution function corresponding to the true

density

f (x) is given by

F(x) =

−∞

f (t) dt .

The distribution function corresponding to the Dirac

mixture approximation can be written as

F(x, η) =

−∞

f (t, η) dt =

∑

i=1

H(x − x

) , (2)

where H(.) denotes the Heaviside function deﬁned as

H(x) =







0, x < 0

, x = 0

1, x > 0

A suitable distance measure is given by the

weighted Cram

er–von Mises distance (Boos, 1981)

G(η) =

∞

−∞

r(x)



F(x) − F(x, η)



dx , (3)

where r(x) is a nonnegative weighting function. r(x)

will later in the ﬁlter step be selected in such a way

that only those portions of the predicted probability

density function having support by the likelihood, are

approximated with high accuracy. This avoids to put

much approximation effort into irrelevant regions of

the state space.

The goal is now to ﬁnd a parameter vector η that

minimizes (3) according to η = arg min

G(η). Un-

fortunately, it is not possible to solve this optimiza-

tion problem directly. Hence, we apply a progressive

method introduced in (Schrempf et al., 2006b). For

this approach, we introduce a so called progression

parameter γ into

F(x) that goes from 0 . . . 1. The pur-

pose of this parameter is to ﬁnd a very simple and

exact approximation of

F(x, γ) for γ = 0. Further we

must guarantee that

F(x, γ = 1) =

F(x). By varying

γ from 0 to 1 we track the parameter vector η that

minimizes the distance measure.

In order to ﬁnd the minimum of the distance mea-

sure, we have to ﬁnd the root of the partial derivative

with respect to η according to

∂G(η, γ)

∂η





∂G(η,γ)

∂x

∂G(η,γ)

∂w





= 0 . (4)

Together with (2) and (3) this results in the system of

equations

F(x

, γ) =

∑

j=1

H(x

− x

) ,

∞

r(x)

F(x, γ) dx =

∑

j=1

∞

r(x)H(x − x

) dx ,

where i = 1, . . . , L.

In order to track the minimum of the distance mea-

sure we have to take the derivative of (4) with respect

to γ.

This results in a system of ordinary ﬁrst order dif-

ferential equations that can be written in a vector–

matrix–form as

b = P

η , (5)

A STATE ESTIMATOR FOR NONLINEAR STOCHASTIC SYSTEMS BASED ON DIRAC MIXTURE

APPROXIMATIONS

where

b =







∂

F(x

,γ)

∂γ

∂

F(x

,γ)

∂γ

∞

∂

F(x,γ)

∂γ

∞

∂

F(x,γ)

∂γ

∞

∂

F(x,γ)

∂γ







and

η =

∂η

∂γ



˙x

, . . . , ˙x

, ˙w

, . . . , ˙w



η denotes the derivative of η with respect to γ.

The P matrix as well as the derivations are given in

(Schrempf et al., 2006b). The approximation of

f (x)

now boils down to solving (5).

4.2 Prediction Step

We now explain the Bayesian prediction step and

show how the approximation introduced in the last

subsection can be used for closed-form calculations.

Calculating the state densities f

k+1

k = 1, . . . , N, is performed by evaluation the Bayesian

forward step, which is given by

k+1

) =

∞

−∞

f (x

k+1

) f

)dx

, (6)

where the transition density f (x

k+1

) of the con-

sidered nonlinear system with additive noise is given

f (x

k+1

) = f

k+1

− g(x

)) ,

where f

(·) is the density of the system noise (e.g.

Gaussian).

In general, the integral involved in (6) cannot be

solved analytically for arbitrary prior densities f

)

For a given input point ¯x

, however, represented by

the Dirac delta function f

) = δ(x

− ¯x

), (6) can

be solved in closed form according to

k+1

) = f

k+1

− g( ¯x

)) .

In the case of zero mean Gaussian system noise

with

(w) = N (w, 0, σ

) ,

this yields

k+1

) = N (x

k+1

, g( ¯x

), σ

) ,

which is a Gaussian Density with a standard deviation

For a given Dirac mixture prior f

) according

to (1) given by

) =

∑

i=1

(i)

δ(x

− x

(i)

) , (7)

the posterior according to (6) is a Gaussian mixture

given by

k+1

) =

∑

i=1

(i)



k+1

, g(x

(i)

), σ



which is a closed-form solution.

Please note, that similar result can be derived for

non-additive and non-Gaussian noise.

4.3 Filter Step

The ﬁlter step consists of fusing the predicted den-

sity f

) and the likelihood function f

, ˆy

)

governed by the measurement ˆy

according to

) = c · f

)· f

, ˆy

) , (8)

where c is a normalizing constant. The likelihood

function is given by

, ˆy

) = f ( ˆy

) .

For a nonlinear system with additive noise, the condi-

tional density for the measurement f (y

) is given

f (y

) = f

− h(x

)) ,

where f

(·) is the density of the measurement noise

and h(x

) is the nonlinear measurement function. In

the case of zero-mean Gaussian measurement noise

the likelihood function can be written as

, ˆy

) = N ( ˆy

, h(x

), σ

) .

We would like to emphasize, that in the general

nonlinear case this likelihood function is no proper

density function. Furthermore, a parametric represen-

tation of this function is not available in general. This

is the reason, why the update equation (8) cannot be

solved analytically, even if the prediction is given in a

parametric representation.

Our solution to this problem is driven by the same

observation made for solving the prediction step in

Sec. 4.2. The likelihood can be evaluated at certain

points ¯x

, which yields constant values.

In order to calculate the product of a likelihood

and a prediction, where the latter is already given as a

Dirac mixture, it comes quite naturally to use the x

(i)

points of the Diracs to evaluate the likelihood. The

obtained values of f

(·) can then be used to reweight

the predicted density according to

) =

∑

i=1

¯w

(i)

δ(x

− x

(i)

)

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

with

¯w

(i)

= c ·w

(i)

· f

( ˆy

− h(x

(i)

)) ,

where w

(i)

is the i’th weight and x

(i)

is the i’th po-

sition of the approximated prediction f

). The

normalization constant can be calculated as

c =

∑

i=1

(i)

· f

( ˆy

− h(x

(i)

))

−1

Naive approximation of the predicted density in a

ﬁxed interval may lead to many small weights, since

not all regions of the state space supported by the pre-

diction are as well supported by the likelihood. This

phenomenon can be described as parameter degrada-

tion. To circumvent this problem, we make use of

the weighting function r(x) in (3). Details on this

approach are presented in the next section.

5 OPTIMAL NUMBER OF

PARAMETERS

In this section, we describe how to tackle the prob-

lem of parameter degradation that is inherent to all

ﬁlter approaches considering only discrete points of

the density. We further describe a method for ﬁnding

an optimal number of components for the approxima-

tion taking into account the prediction and ﬁlter steps

as well.

To ﬁght the problem of parameter degradation de-

scribed in the previous section we make use of the

fact, that although the likelihood function is not a den-

sity it decreases to zero for x → ±∞ in many cases.

An example for this are polynomial systems suffer-

ing from additive noise. Therefore, we can deﬁne

an area of support for which the likelihood is higher

than a certain value. This area of support is an in-

terval and can be represented by the weighting func-

tion r(x) in (3). It guarantees, that all components of

the approximation are located in this interval and are

therefor not reweighed to zero in the ﬁlter step. In

other words, the complete mass of the approximation

function accounts for the main area of interest.

In (Schrempf and Hanebeck, 2007), we intro-

duced an algorithm for ﬁnding the optimal number

of components required for the approximation with

respect to the following prediction step. We will

now extend this algorithm in order to account for the

preceding ﬁlter step as well.

At the beginning of Algorithm 1 in line 6, an ini-

tial approximation with a very large number of com-

ponents is generated and passed through the predic-

tion step, resulting in a continuous density representa-

tion with parameter vector κ

. Due to the high number

Algorithm 1 Optimal number of components w.r.t.

the ﬁlter step and posterior density.

1: Select max. Error Threshold G

max

2: Select initial number of Components L = L

3: Select search step ∆L

4: f

(x) = likelihood( ˆy)

5: r(x) = support( f

(x))

6: κ

= predict(ﬁlter(approx(L

large

,r(x)), ˆy))

7: while G > Gmax do

8: κ = predict(ﬁlter(approx(L,r(x)), ˆy))

9: G = G(κ

, κ)

10: L = L + ∆L

11: end while

12: L

= L − 2∆L

13: L

= L − ∆L

14: while L

− L

> 1 do

15: L

= L

+ b

−L

16: κ = predict(ﬁlter(approx(L

,r(x)), ˆy))

17: G = G(κ

, κ)

18: if G > G

max

then

19: L

= L

20: else

21: L

= L

22: end if

23: end while

of components we can assume this density to be very

close to the true density. An efﬁcient procedure for

approximating arbitrary mixture densities with Dirac

mixtures comprising a large number of components is

given in (Schrempf and Hanebeck, 2007).

In each search step of the algorithm, the distance

measure of the approximated density at hand to the

density deﬁned by κ

is calculated. In this way the

smallest number of components for a prespeciﬁed

error can be found.

6 EXPERIMENTAL RESULTS

In order to compare the performance of our ﬁlter to

other state-of-the-art ﬁlters, we have simulated a non-

linear dynamic system according to the left part of

Figure 1. We apply the ﬁlter to a strongly nonlinear

cubic system and measurement function motivated by

the cubic sensor problem introduced in (Bucy, 1969).

The simulated system function is

g(x

) = 2x

− 0.5x

+ w

and the additive noise is Gaussian with σ

= 0.2

standard deviation. The measurement function is

h(x

) = x

− 0.5x

+ v

A STATE ESTIMATOR FOR NONLINEAR STOCHASTIC SYSTEMS BASED ON DIRAC MIXTURE

APPROXIMATIONS

−2 0 2

0.2

0.4

0.6

0.8

(x)

k=1 L=17

−2 0 2

0.2

0.4

0.6

0.8

(x)

k=2 L=12

−2 0 2

0.2

0.4

0.6

0.8

(x)

k=3 L=29

−2 0 2

0.5

(x)

k=1 L=17

−2 0 2

0.5

(x)

k=2 L=12

−2 0 2

0.5

(x)

k=3 L=29

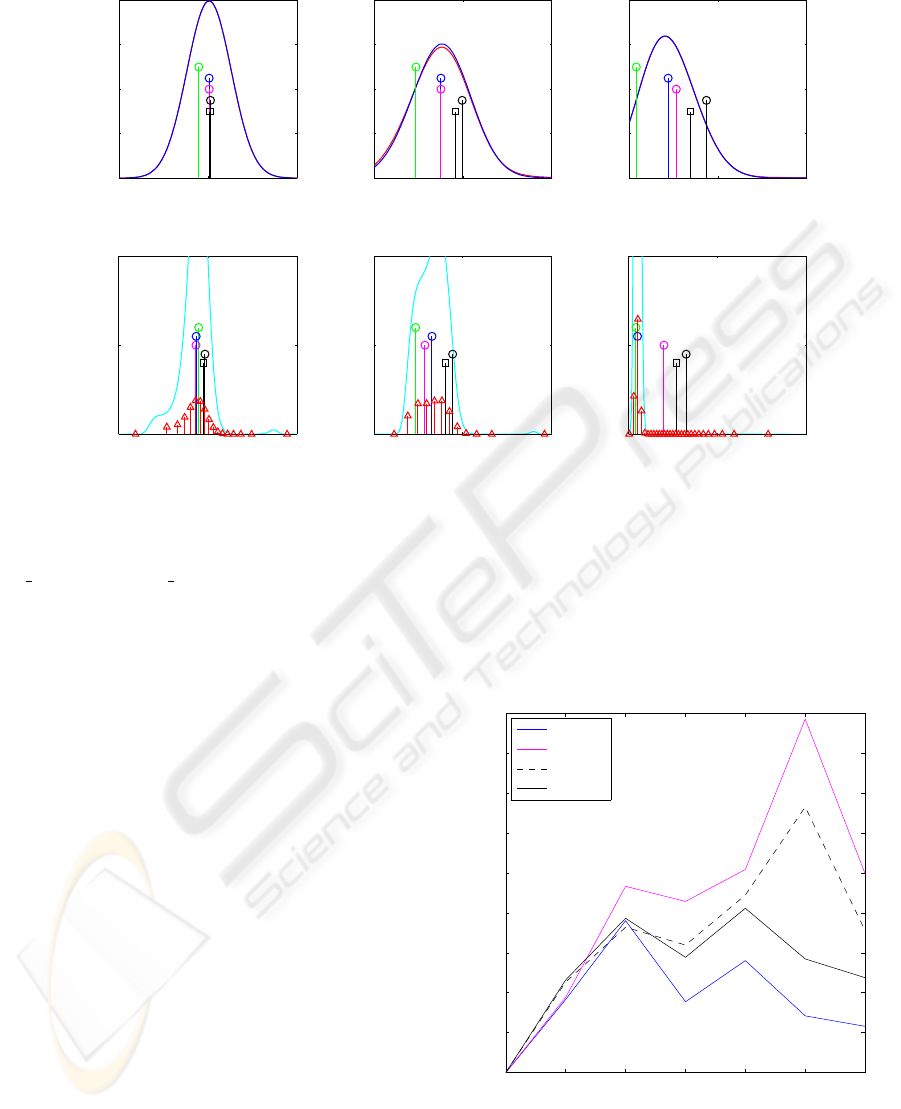
Figure 2: The recursive ﬁlter for T = 3 steps. k indicates the step number and L the number of components for the Dirac

mixture. The upper row shows the prediction steps, the lower row shows the ﬁlter steps. Upper row: The blue is the

continuous density predicted by the DM ﬁlter, the red line underneath is the true density. The green marker depicts the true

(simulated) system state, the other markers depict the predicted point estimates of the following ﬁlters: blue=DM, pink=UKF,

black circle=PF20, black square=PF1000. Lower row: The cyan line shows the likelihood. The colors of the point estimates

are similar to the upper line.

with additive Gaussian noise and σ

= 0.5.

The generated measurements are used as input to

our ﬁlter as well as to an unscented Kalman ﬁlter and

a particle ﬁlter. The particle ﬁlter is applied in a vari-

ant with 20 particles and a variant with 1000 particles

in order to compare the performance.

In a ﬁrst run of the experiment we show T = 3

steps in Figure 2. The upper row shows the predic-

tion steps, the lower row shows the corresponding ﬁl-

ter steps. The continuous prediction f

k+1

) of the

Dirac mixture (DM) ﬁlter is depicted by the dark blue

line. The red line underneath shows the true predic-

tion computed numerically as a reference. The cyan

plot in the lower line shows the likelihood given by

the current measurement and the red arrows depict the

Dirac mixture after the ﬁlter step.

Both rows also show the point estimates of the

various applied ﬁlters in the current step. The green

marker indicates the true (simulated) state, whereas

blue stands for the Dirac mixture point estimate. Pink

is the UKF estimate an black are the particle ﬁlter es-

timates. The particle ﬁlter indicated by the circle uses

20 particles, the one indicated by the square uses 1000

particles.

We simulated the system a further 10 times for

T = 7s in order to calculate the root means square

error e

rms

of the 4 ﬁlters. The results are shown in

Figure 3. The plot shows that the point estimates of

1 2 3 4 5 6 7

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

rms

UKF

PF20

PF1000

Figure 3: Root mean square error f or 10 runs and T = 7

steps.

the Dirac mixture ﬁlter are much closer to the true

state than the point estimates of the other ﬁlters.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

7 CONCLUSION

In this paper, we presented a complete Dirac mixture

ﬁlter that is based on the approximation of the poste-

rior density. The ﬁlter makes use of the properties of

the Dirac mixture approximation wherever they are

required, but does not deny the continuous charac-

ter of the true density. This can especially be seen

after each prediction step, where the full continuous

density representation is used.

The new approach is natural, mathematically rig-

orous, and based on an efﬁcient algorithms (Schrempf

et al., 2006a)(Schrempf et al., 2006b) for the op-

timal approximation of arbitrary densities by Dirac

mixtures with respect to a given distance.

Compared to a particle ﬁlter, the proposed method

has several advantages. First, the Dirac components

are systematically placed in order to minimize a given

distance measure, which is selected in such a way that

the future evolution of approximate densities is al-

ways close to the true density while also considering

the actual measurements. As a result, very few sam-

ples are sufﬁcient for achieving an excellent estima-

tion quality. Second, the optimization does not only

include the parameters of the Dirac mixture approxi-

mation, i.e., weights and locations, but also the num-

ber of components. As a result, the number of compo-

nents is automatically adjusted according to the com-

plexity of the underlying true distribution and the sup-

port area of a given likelihood. Third, as the approxi-

mation is fully deterministic, it guarantees repeatable

results.

Compared to the Unscented Kalman Filter, the

Dirac mixture ﬁlter has the advantage, that it is not

restricted to ﬁrst and second order moments. Hence,

multi-modal densities, which cannot be described suf-

ﬁciently by using only the ﬁrst two moments, can

be treated very efﬁciently. Such densties occur quite

often in strongly nonlinear systems. Furthermore,

no assumptions on the joint distribution of state and

measurement have to be made.

REFERENCES

Alspach, D. L. and Sorenson, H. W. (1972). Nonlinear

Bayesian Estimation Using Gaussian Sum Approxi-

mation. IEEE Transactions on Automatic Control,

AC–17(4):439–448.

Boos, D. D. (1981). Minimum Distance Estimators for Lo-

cation and Goodness of Fit. Journal of the American

Statistical association, 76(375):663–670.

Bucy, R. S. (1969). Bayes Theorem and Digital Realiza-

tions for Non-Linear Filters. Journal of Astronautical

Sciences, 17:80–94.

Doucet, A., Freitas, N. D., and Gordon, N. (2001). Se-

quential Monte Carlo Methods in Practice. Springer-

Verlag, New York.

Doucet, A., Godsill, S., and Andrieu, C. (2000). On Se-

quential Monte Carlo Sampling Methods for Bayesian

Filtering. Statistics and Computing, 10(3):197–208.

Geweke, J. (1989). Bayesian Inference in Econometric

Models using Monte Carlo Integration. Econometrica,

24:1317–1399.

Gordon, N. (1993). Bayesian Methods for Tracking. PhD

thesis, University of London.

Hanebeck, U. D., Briechle, K., and Rauh, A. (2003). Pro-

gressive Bayes: A New Framework for Nonlinear

State Estimation. In Proceedings of SPIE, volume

5099, pages 256–267, Orlando, Florida. AeroSense

Symposium.

Huber, M., Brunn, D., and Hanebeck, U. D. (2006). Closed-

Form Prediction of Nonlinear Dynamic Systems by

Means of Gaussian Mixture Approximation of the

Transition Density. In International Conference on

Multisensor Fusion and Integration for Intelligent

Systems (MFI 2006), Heidelberg, Deutschland, pages

98–103.

Huber, M. F. and Hanebeck, U. D. (2007). Hybrid Tran-

sition Density Approximation for Efﬁcient Recursive

Prediction of Nonlinear Dynamic Systems. In In-

ternational Conference on Information Processing in

Sensor Networks (IPSN 2007), Cambridge, USA.

Julier, S. and Uhlmann, J. (1997). A New Extension of

the Kalman Filter to Nonlinear Systems. In Proceed-

ings of SPIE AeroSense, 11th International Sympo-

sium on Aerospace/Defense Sensing, Simulation, and

Controls, Orlando, FL.

Kullback, S. and Leibler, R. A. (1951). On Information

and Sufﬁciency. Annals of Mathematical Statistics,

22(2):79–86.

Schrempf, O. C., Brunn, D., and Hanebeck, U. D. (2006a).

Density Approximation Based on Dirac Mixtures with

Regard to Nonlinear Estimation and Filtering. In Pro-

ceedings of the 45th IEEE Conference on Decision

and Control (CDC’06), San Diego, California, USA.

Schrempf, O. C., Brunn, D., and Hanebeck, U. D. (2006b).

Dirac Mixture Density Approximation Based on Min-

imization of the Weighted Cram

er–von Mises Dis-

tance. In Proceedings of the International Confer-

ence on Multisensor Fusion and Integration for In-

telligent Systems (MFI 2006), Heidelberg, Germany,

pages 512–517.

Schrempf, O. C. and Hanebeck, U. D. (2007). Recursive

Prediction of Stochastic Nonlinear Systems Based on

Dirac Mixture Approximations. In Proceedings of the

American Control Conference (ACC ’07), New York

City, USA.

A STATE ESTIMATOR FOR NONLINEAR STOCHASTIC SYSTEMS BASED ON DIRAC MIXTURE

APPROXIMATIONS