ARTIFICIAL IMMUNE FILTER FOR VISUAL TRACKING
Alejandro Carrasco E. and Peter Goldsmith
Mechanical Enginering, University of Calgary, 2500 University Drive NW, Calgary, Canada
Keywords: Filtering, visual tracking, immune system, artificial intelligence.
Abstract: Visual tracking is an important part of artificial Vision for robotics. I
t allows robots to move towards a
desired position using real world information. In this paper we present a novel particle filtering method for
visual tracking, based on a clonal selection and a somatic mutation processes used by the natural immune
system, which is excellent at identifying intrusion cells; antigens. This capability is used in this work to
track motion of the object in a sequence of images.
1 INTRODUCTION
Artificial intelligence has found a source of ideas
borrowed from biological systems such as swarms,
ant colonies, neural networks, genetic algorithms
and immune systems. They have been successfully
used in many different areas: control (Macnab,
2000), optimization (Charbonneau, 2002), pattern
recognition (Tashima, 2001), robotics (Ramirez-
Serrano, 2004) and prediction (Connor, 1994). The
immune system is composed of a complex
constellation of cells, organs and tissues, arranged in
an elaborate and dynamic communications network
and equipped to optimize the response against
invasion by pathogenic organisms. The immune
system is, in it simplest form, a cascade of detection
and adaptation culminating in a system that is
remarkably effective, most of the time. It has many
facets, a number of which can change to optimize
the response to these unwanted intrusions (Dasgupta,
2002). The immune system has a series of dual
natures, the most important of which is self - non-
self recognition. The others are: general - specific,
natural - adaptive, innate - acquired, cell_mediated -
humoral, active – passive and primary - secondary.
Parts of the immune system are antigen-specific
(they recognize and act against particular antigens),
systemic (not confined to the initial infection site,
but work throughout the body), and have memory
(recognize and mount an even stronger attack to the
same antigen the next time) (Gilbert, C. , 1994). It
can recognize and remember millions of different
enemies, and it can produce secretions and cells to
match up with and wipe out each one of them. The
secret to its success is an elaborate and dynamic
communications network (de Castro, 2002). Millions
and millions of cells, organized into sets and subsets,
gather like clouds of bees swarming around a hive
and pass information back and forth. The key to a
healthy immune system is its remarkable ability to
distinguish between the body’s own cells and
foreign cells (Bergstrom, 2004). The body’s immune
defences normally coexist peacefully with cells that
carry distinctive “self” marker molecules. But when
immune defenders encounter cells or organisms
carrying markers that say “foreign,” they quickly
launch an attack. In this work, we use the intruder
detection capability of artificial immune systems in
order to track the object in a sequence of images.
2 VISUAL TRACKING
Visual tracking is the action of consistently locating
a desired feature in each image of an input sequence.
The problem is typically complicated by sensor
noise, motion in the scene, motion on the part of the
observer and real-time constraints. The problem can
be further complicated when more than one identical
feature must be tracked, in which case it is up to the
observer to decide the optimal set of
correspondences which are consistent with a priori
assumptions about, and recent observations of, the
behavioural characteristics of the features (Prassler,
1990)(Carlsson, 1990). Given an image
, the problem is to track a sub-image
(object). In a sequence of images the object will be
+
ℵ∈jijiI ,),(
280
Carrasco E. A. and Goldsmith P. (2007).
ARTIFICIAL IMMUNE FILTER FOR VISUAL TRACKING.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 280-285
DOI: 10.5220/0001630102800285
Copyright
c
 SciTePress

in different positions, moving in a determined
pattern. Therefore the prediction part of the filter is
needed to predict where the object I(u,v) will be in
the image I(i,j), giving a region of interest to
accelerate the processing of recognizing the object.
Recognizing the object by filtering the clutter and
noise due to change of illumination, shadows, etc. is
the second part of the filter. The use of filters such
as the Kalman filter (Gutman, 1990)(Welch, 2001),
which is based in optimal prediction for linear
system and noise with Gaussian distribution, are
excellent tools to overcome the problems in visual
tracking. Extensions of the Kalman filter for non-
linear systems have been developed such as
Extended Kalman filter (Ribeiro, 2004) and
Unscented Kalman filter (Jeffrey, 1997). Another
algorithm of interest is the condensation
(Conditional Density Propagation) (Isard, 1998),
which is based on computing the Bayes’ rule to a set
of particles (particle filtering). In general the filters
mentioned above can be seen as Bayesian filters,
where the following density distributions are needed
(Isard, 1996) (Grewal, 1993):
)|(
kk
Zxp
: A posteriori density given the measurement.
)|(
1−kk
Zxp
: A priori density.
)|(
1−kx
xxp
: Process density describing the dynamics.
)|(
kk
xzp
: Observation density
Bayes’ Rule is
∫
∫
−
−−−
=
kkkkk
kkkkkkk
kk
dxZxpxzp
dxZxpxxpxzp
Zxp
)|()|(
)|()|()|(
)|(
1
111
(1)
One of the drawbacks in these algorithms is the
assumption of priori density distribution, Gaussian
distribution such in the case of Kalman filter.
Particle filters use Bayes (equation 1) and Monte
Carlo method to approximate the sequence of
probability distribution; these required a large
number of particles to converge towards the
probability distribution. Therefore, the random
sampling is the main drawback, due to in case that
the population is not drawn to represent some of its
statistical features makes a wrong estimation.
Besides, due to the degeneration of the particles
through time, re-sampling mechanisms are used. In
the next section we introduce an artificial immune
system to filter noisy signals and predict the state of
a system.
3 ARTIFICIAL IMMUNE FILTER
(AIF): CLONAL SELECTION
AND SOMATIC MUTATION
The clonal selection theory, by immunologist Frank
Macfarlane Burnet (Burnet, 1978), models the
principles of an immune system. When an antigen is
present in our body, the B-Lymphocyte cells
produce antibodies Ab receptors. Each B cell has a
specific antibody as a cell surface receptor. The
arrangement and generation of antibody genes
occurs prior to any exposure to antigen. When a
soluble antigen is present, it binds to the antibody on
the surface of B cells that have the correct
specificity. These B cell clones develop into
antibody-producing plasma cells or memory cells.
Only B cells, which are antigen-specific, are capable
of secreting antibodies. Memory cells remain in
greater numbers than the initial B cells, allowing the
body to quickly respond to a second exposure of that
antigen, as show in Figure 1 (de Castro, 2002).
Figure 1: Clonal Selection Principle.
The higher affinity comes from a mechanism
that alters the variable regions of the memory cells
by specific somatic mutation. This is a random
process that by chance can improve antigen binding.
This same principle is the inspiration in this work to
produce an artificial immune filter. Initial set of n B-
cells (particles) , representing the
features of our object to track (positions, velocity,
etc), weights , representing its
affinity between the antigens and the antibodies, and
memory cells , are created. In the
beginning our best affine cell to our antigen is our
),...,,(
11 n
xxxX =
),...,,(
21 n
wwwW =
),...,,(
21 m
sssS =
ARTIFICIAL IMMUNE FILTER FOR VISUAL TRACKING
281

initial condition. Therefore we clone and slightly
mutate the cell, using equation (2)
i
k
best
k
i
k
rxx α +=
(2)
where r is a random variable normally distributed
and
)1,0(~ Nr ℜ∈
α
is a small constant. The
affinity is integrated by two distance
measurements from our best B cell, before and after
prediction. Equation (3) is the first part of affinity
i
w
(
)
i
k
best
k
i
xxaf −−= exp
1
(3)
The next step k+1 is the prediction part, given by
for nonlinear dynamics and by
for linear dynamics, where A is known
as the transition matrix. After all the cells have been
through the dynamic system, it is time to obtain a
new measurement , which contains a certain level
of noise. Then we apply equation (4) to obtain the
second part of our affinity measurement, where H is
the observation model in the case of a linear system
and
)(
1
i
k
i
k
xfx =
+
i
k
i
k
Axx =
+1
k
z
β
is a constant.
(
)
i
kk
i
Hxzaf
12
exp
+
−−= β
(4)
ii
i
afafw
21
+=
(5)
Equation (5) calculates the affinity of each B-cell to
the antigen. The m best cells with high affinity will
conform to our memory cells, and the highest
affinity will be the estimation
1+k
x

and our next best
B-cell .
best
k
x
1+
3.1 Application of Artificial Immune
Filter to Noise Rejection
Before applying the artificial immune system to
visual tracking, the filter was tested on a noisy signal
and compared to a Kalman filter. The signal
represents the antigen to be recognized. The best B-
cell that binds the antigen is the estimation of the
state of the signal. The next stage is choosing the
parameter for mutation,
α
. Since the level of
somatic mutation for the cells is a slight change on
our best B-cell, a value equal or less than dt value,
the step time of the system, is a good option,
because it indicates that B-cells could vary
(0.01 for this example) from their real values.
Given a linear stochastic difference equation in the
next form
dt±
kkkk
wbuAxx +
+
=
+1
(6)
kkk
vHxz
+
=
(7)
where
⎥
⎦
⎤
⎢
⎣
⎡
−
=
1
1
dt
dt
A
⎥
⎦
⎤
⎢
⎣
⎡
=
0
0
b
[] 01=H 0
=
k
u
Noise is modelled by
⎥
⎦
⎤
⎢
⎣
⎡
⋅⋅
⋅⋅
=
k
k
k
rdt
rdt
w
15.0
15.0
2
(8)
[
] )sinh(05.01.0
kk
rv
+
=
(9)
Equation (9) introduce a heavily spike noise with
non zero mean, while equation (8) is a normal
distribution, and r is random noise. Figure 2 shows
the measured position with noise up to 50% of its
maximum value.
Figure 2: Measured position.
Using the proposed algorithm of Figure 3, we
obtained the filtered signal in Figure 4.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
282

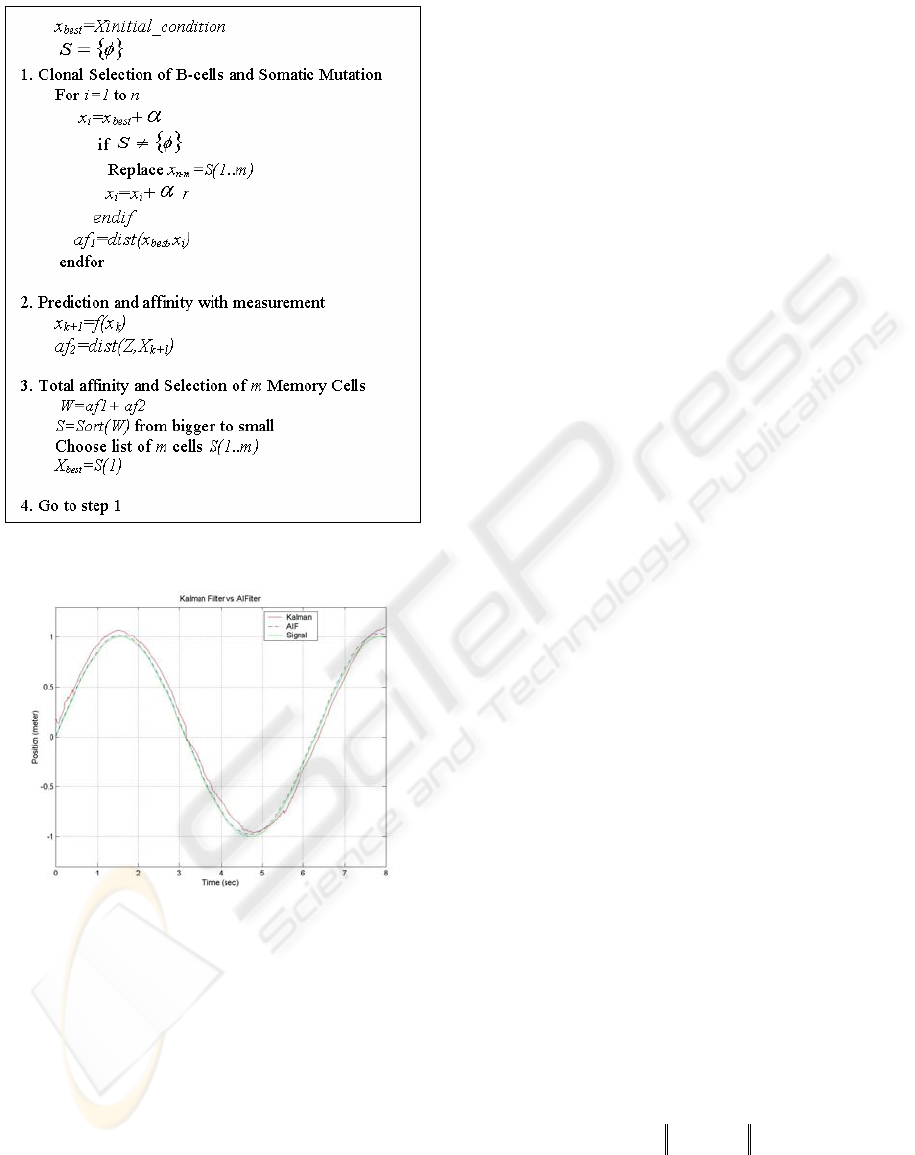
Figure 3: Pseudo-code for Artificial Immune Filter.
Figure 4: Performance of Filters.
It is well known that the uncertainty of the
covariance parameters of the process noise, Q, and
the observation errors, R, has a significant impact on
Kalman filtering performance. Q and R influence the
weight that the filter applies between the existing
process information and the latest measurements.
Errors in any of them may result in the filter being
suboptimal or even cause it to diverge. The
conventional way of determining Q and R requires
good a priori knowledge of the process noises and
measurement errors, which normally comes from
intensive empirical analysis. Besides of the errors
due to covariance parameters, the Kalman filter is
based on the assumption of normal distribution noise
with zero mean. Figure 4 shows the real signal with
no noise and the filtered signal. It can be seen that
the filter affectively attenuated the noise. In this
example we use the following parameter settings for
the Kalman filter,
⎥
⎦
⎤
⎢
⎣
⎡
=
00015.0015.0
015.000015.0
Q
0025.0=R QP
=
The parameter settings for the AIF were, n=20,
m=5,
[
]
01.001.0001.0
=
α
,
1.0=
β
.
3.2 Visual Tracking using AIF
Tracking an object in a sequence of images is a
challenging problem. An elementary tracking
approach could be to fit a curve, (contour of an
object) to each image in a sequence, and an
estimated curve is therefore required for each image.
Then a fitted curve from one image is the estimation
for the next image. This kind of algorithm will be
affected by fast motion and become sensitive to
distractions. Clutter in the background, either static
or dynamic, noise of the sensor and change of
illumination, are some factors to consider as noise in
an image (Healey, 1994). The tracking performance
can be greatly improved by a filter able to predict
and correct the fitted curve, removing the noise from
the image. Our artificial immune filter is used in this
section to track an object in a sequence of images.
The extension of the artificial immune filter from
single variable to multivariable is straightforward.
The contour of the object is a parametric curve
(
)
(
)
(
) tIytIxtc ,)(
=
[] Lt ,0∈
(10)
where t is an independent parameter over the
interval [0,L], and Ix(t) and Iy(t) are known as spline
functions (Foley, 1990). An important aspect to
achieve real time tracking performance has been the
restriction of measurements of the set of
observations Z to a sparse set of lines normal to the
contour of the object, as shown in Figure 5. In this
case the affinity is given by
()
(
)
∑
=
−−=
P
j
i
k
j
k
i
tCzaf
1
2
exp
(11)
where P is the number of searching lines and is
the edge closest to the hypothetical contour
j
k
z
(
) tC
i
k
.
ARTIFICIAL IMMUNE FILTER FOR VISUAL TRACKING
283

Figure 5: Normal lines of object contour to search the
observation z
i
.
Figure 6 shows a sequence for fast tracking motion
of a ball with clutter added to background. This
experiment used 100 cells and 10 memory cells, in
real time (30 frames per second). In spite of the fast
motion of the ball, the tracker never loses contact
with the ball in a sequence of image, when we
bounced the ball several times against the wall. The
tracker shows the center of the ball with white dots.
Figure 6: Tracking a fast motion ball.
Figure 7 is a group of snapshots from a tracking
sequence of the ball under heavy clutter, dynamic
background and partial occlusion.
Figure 7: Tracking using Artificial Immune Filter.
4 CONCLUSIONS
In this work we introduced a novel filter using a
clonal selection and somatic mutation model of
immune system. The filter does not require
probability distributions or re-sampling, unlike other
particle filters. The artificial immune filter was
tested for signal processing and visual tracking,
showing good performance in both applications. In
the application of visual tracking of the ball, the
filter was able to track fast ball motion in a non-
smooth trajectory (bouncing) and clutter in the
background. Future work will include the adaptation
of parameters and tracking of several objects.
ACKNOWLEDGEMENTS
We would like to thanks to CONACyT for its
support in this research.
REFERENCES
Macnab, C.J.B., D'Eleuterio, G.M.T., May 2000, Discrete-
time Lyapunov design for neuro-adaptive control of
elastic-joint robots, International Journal of Robotics
Research vol. 19, no. 5, pp. 511-525.
Paul Charbonneau, 2002, An Introduction to Genetic
Algorithms for Numerical Optimization, National
Center for Atmospheric Research, Boulder, Colorado.
Koichi Tashima, Zheng Tang, Okihiko Ishizuka, Koichi
Tanno, 2001, An immune network with interactions
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
284

between B cells for pattern recognition. Scripta
Technica, Syst Comp Jpn, 32(10): 31-41.
Ramirez-Serrano, A., and Pettinaro G.C., 2004, "Origami
robotics: swarm robots that can fold into diverse
configurations", Mechatronics2004, pp. 171-182,
Ankara, Turkey, August 30 - September 1.
Jerome T. Connor, R. Douglas Martin, 1994, Recurrent
Neural Networks and Robust Time Series Prediction.
IEEE Transactions on Neural Networks, Vol. 5 , No.
2.
Dasgupta, D., Gonzalez, F., 2002, An immunity-based
technique to characterize intrusions in computer
networks, IEEE Trans. Evol. Comput. 6:1081–1088.
Gibert, C. J. & Routen, T. W. 1994, Associative memory
in an immune-based system. In: Proceedings of the
Twelfth National Conference on Artificial Intelligence
pp. 852–857, Cambridge, MA. AAAI Press/The MIT
Press.
de Castro, L. N. and Von Zuben, F. J., 2002, Learning and
optimization using the clonal selection principle, IEEE
Trans. Evol. Comput. Special issue on artificial
immune systems, 6:239–251.
Carl T. Bergstrom, Rustom Antia, 2004, How do adaptive
immune systems control pathogens while avoiding
autoimmunity? Department of Biology, University of
Washington.
E. Prassler, J. Scholz, M. Schuster, and D. Schwammkrug,
June 1998, Tracking a large number of moving object
in a crowded environment, Proceedings of the IEEE
Workshop on Perception for Mobile Agents (Santa
Barbara) (G. Dudek, M. Jenkin, and E. Milios, eds.),
pp. 28-36.
S.Carlsson and J.O. Eklundh, 1990, Object detection using
model based prediction and motion parallax,
Proceedings of the European Conference on Computer
Vision (Antibes), Springer-Verlag, pp. 297-206.
Gutman, P., Velger, M., 1990, Tracking Targets Using
Adaptive Kalman Filtering, IEEE Transactions on
Aerospace and Electronic Systems Vol. 26, No. 5: pp.
691-699.
Welch, G, Bishop, G., 2001, An Introduction to the
Kalman Filter, ACM, IGGRAPH 2001, Course8,
www.cs.unc.edu/welch/kalman.
Maria Isabel Ribeiro, 2004, Kalman and Extended Kalman
Filters: Concept, Derivation and Properties. Institute
for Systems and Robotics. Lisboa PORTUGAL.
Simon J. Julier Jeffrey K. Uhlmann, 1997, A New
Extension of the Kalman Filter to Nonlinear Systems.
The Robotics Research Group, Department of
Engineering Science, The University of Oxford.
M. Isard and A. Blake, 1998, CONDENSATION:
Conditional Density Propagation for visual tracking,
International Journal of Computer Vision, Vol. 29, No.
1, pp. 5-28.
M. Isard and A. Blake, 1996, Contour tracking by
stochastic propagation of conditional density. In
European Conference on Computer Vision, volume 1,
pages 343–356.
M. S. Grewal and A. P. Andrews, 1993, Kalman Filtering.
Prentice Hall.
Burnet, F. M., 1978, “Clonal Selection and After”, In
Theoretical Immunology, (Eds.) G. I. Bell, A. S.
Perelson & G. H. Pimbley Jr., Marcel Dekker Inc., 63-
85.
Leandro Nunes de Castro, Fernando J. Von Zuben, 2002,
The Clonal Selection Algorithm with Engineering
Applications. School of Electrical and Computer
Engineering, State University of Campinas, Brazil.
G. Healey, R. Kondepudy, 1994,"Radiometric CCD
camera calibration and noise estimation", IEEE
Transactions on Pattern Analysis and Machine
Intelligence, Vol. 16, No. 3, pp. 267-276.
Foley, J., van Dan, A., Feiner, S., and Hughes, J.,
1990,Computer Graphics: Principles and Practice,
chapter 13, 563-604, Addison-Wesley.
ARTIFICIAL IMMUNE FILTER FOR VISUAL TRACKING
285