AUTOMATIC ESTIMATION OF PARAMETERS FOR THE

HIERARCHICAL REDUCTION OF RULES OF COMPLEX

FUZZY CONTROLLERS

Yulia Ledeneva

Instituto Politecnico Nacional, Center of Investigation in Computing, Unidad Adolfo López Mateos,D.F., México

Carlos A. Reyes-García, Alejandro Díaz-Méndez

Instituto Nacional de Astrofísica, Óptica y Electrónica, Luis Enrique Erro, Puebla, México

Keywords: Fuzzy control, rule base reduction, hierarchical method, genetic algorithm.

Abstract: The application of fuzzy control to large-scale complex systems is not a trivial task. For such systems the

number of the fuzzy IF-THEN rules exponentially explodes. If we have m linguistic properties for each of n

variables, we will have m

rules combinations of input values. Large-scale systems require special

approaches for modelling and control. In our work the system’s hierarchical structure is studied in an

attempt to reduce the size of the inference engine for large-scale systems. This method reduces the number

of rules considerably. But, in order to do so, the adequate parameters should be estimated, which, in the

traditional way, depends on the experience and knowledge of a skilled operator. In this work, we are

proposing a method to automatically estimate the corresponding parameters for the hierarchical rule base

reduction method to be applied to fuzzy control complex systems. In our approach, the parameters of the

hierarchical structure are found through the use of genetic algorithms. The implementation process, the

simulation experiments and some results are presented.

1 INTRODUCTION

Since the first fuzzy controller was presented by

Mamdani in 1974, the different studies devoted to

the theory of fuzzy control have shown that the area

of development of fuzzy control algorithms has been

the most active area of research in the field of fuzzy

logic in the last years. From the decade of the 80´s,

fuzzy logic has performed a vital function in the

advance of practical and simple solutions for a great

diversity of applications in engineering and science.

Some fuzzy control applications to industrial

ocesses have produced results superior to its

equivalent obtained by classical control systems.

The domain of these applications has experienced a

serious limitation when expanding it to more

complex systems, because a complete theory to

determine the performance of the systems when

there is a change in its parameters or variables does

not yet exist.

When some of these applications are designed

r more complex systems, the number of fuzzy

rules controlling the process is exponentially

increased with the number of variables related to the

system. For example, if there are n variables and m

possible linguistic values for each variable, m

fuzzy

rules would be needed to construct a complete fuzzy

controller. As n grows, the rule base quickly

overloads the memory of any computing device,

causing difficulties in the implementation and

application of the fuzzy controller.

A hierarchical structure is studied in an attempt

to reduce the size of the infe

rence engine for large-

scale systems. This structure reduces considerably

the number of rules. However, the adequate

parameters should be estimated. In traditional

techniques much reliance has to be put on the

experience of the system designer in order to find a

good set of parameters (Jamshidi M., 1997).

Genetic algorithms (GA) are an appropriate

technique to

find parameters in a large search space.

They have shown efficient and reliable results in

solving optimization problems. For these reasons, in

this work we estimate the parameters needed for the

rule base reduction method by means of GAs.

The paper is organized as follows. Section 2

summ

arizes the principles of rule base reduction

methods. In Section 3, the hierarchical structure is

398

Ledeneva Y., A. Reyes-García C. and Díaz-Méndez A. (2007).

AUTOMATIC ESTIMATION OF PARAMETERS FOR THE HIERARCHICAL REDUCTION OF RULES OF COMPLEX FUZZY CONTROLLERS.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 398-401

DOI: 10.5220/0001630603980401

 SciTePress

described. Section 4 proposes the GA which allows

us to automatically find the parameters for the

hierarchical structure in order to improve the

complex fuzzy control system performance. The

results are presented in Section 5.

2 RULE BASE REDUCTION

METHODS

The size of the rule base of complex fuzzy control

systems grows exponentially with the number of

input variables. Due to that fact, the reduction of the

rule base is a very important issue for the design of

this kind of controllers. Several rule base reduction

methods have been developed to reduce the rule

base size. For instance, fuzzy clustering is

considered to be one of the important techniques for

automatic generation of fuzzy rules from numerical

examples (Bezdek, 1974). However, for control

applications, often there is not enough data for a

designer to extract a complete rule base for the

controller.

Anwer (Anwer, 2005) proposed a technique for

generation and minimization of the number of such

rules in case of limited data sets availability. Initial

rules for each data pairs are generated and

conflicting rules are merged on the basis of their

degree of soundness. This technique can be used as

an alternative to develop a model when available

data may not be sufficient to train the model.

A neuro-fuzzy system (Ajith, 2001; Kasabov,

1998; Chia-Feng, 1998; Jang, 1993; Kim, 1999)

is a

fuzzy system that uses a learning algorithm derived

from, or inspired by, neural network theory to

determine its parameters (fuzzy sets and fuzzy rules)

by processing data samples.

Modern neuro-fuzzy

systems are usually represented as special multilayer

feedforward neural networks (for example, models

like ANFIS (Jang, 1993), HyFis (Kim, 1999), etc.).

A disadvantage of these approaches is that the

determination of the number of processing nodes,

the number of layers, and the interconnections

among these nodes and layers are still an art and

lack systematic procedures.

Jamshidi (Jamshidi M., 1997) proposed to use

sensory fusion to reduce a rule base size. Sensor

fusion combines several inputs into one single input.

The rule base size is reduced since the number of

inputs is reduced. Also, Jamshidi proposed to use the

combination of hierarchical and sensory fusion

methods. The disadvantage of the design of

hierarchical and sensory fused fuzzy controllers is

that much reliance has to be put on the experience of

the system designer to establish the needed

parameters. To solve this problem, we automatically

estimate the parameters for the hierarchical method

using GAs.

3 HIERARCHICAL METHOD

When a fuzzy controller is designed for a complex

system, often several measurable output and

actuating input variables are involved. In addition,

each variable is represented by a finite number m of

linguistic labels. This indicates that the total number

of rules is equal to m

, where n is the number of

system variables. As an example, consider n = 4 and

m = 5 than the total number of fuzzy rules will be k

= m

= 5

= 625. If there were five variables, then

we would have k = 3125. From the above simple

example, it is clear that the application of fuzzy

control to any system of significant size would result

in a dimensionality explosion.

In the proposed hierarchical fuzzy control

structure by Jamshidi (Jamshidi M., 1997), the first-

level rules are those related to the most important

variables and are gathered to form the first-level

hierarchy. The second most important variables,

along with the outputs of the first-level, are chosen

as inputs to the second-level hierarchy, and so on.

Figure 1 shows this hierarchical rule structure. The

first and the i-th rule of the hierarchically

categorized sets are given by

IF y

and … and y

THEN u

is BB

where i,j = 1, …,n; y

are the system’s output

variables, u

are the system’s control variables, A

and B

are linguistic labels; and

∑

−

≤=

nnN

is the number of j-th level system variables used

as inputs.

Figure 1: Schematic representation of hierarchical fuzzy

controller.

IF y

Ni+1

is A

Ni1

and … and y

Ni+nj

is A

Ninj

THEN u

Level

Set of rules 1

Set of rules 2

Set of rules L+1

Level

L+1

}

AUTOMATIC ESTIMATION OF PARAMETERS FOR THE HIERARCHICAL REDUCTION OF RULES OF

COMPLEX FUZZY CONTROLLERS

399

The goal of this hierarchical structure is

minimize the number of fuzzy rules from

exponential to linear function. Such rule base

reduction implies that each system variable provides

one parameter to the hierarchical scheme. Currently,

the selection of such parameters is manually done

and becomes a fastidious and time-consuming

routine. In this work, we propose to find these

parameters using genetic algorithms.

4 GENETIC ESTIMATION

Nature has an ability to adapt and learn without

being told what to do. In other words, genetically

nature finds good chromosomes blindly. GAs do the

same. Two mechanisms link a GA to the problem it

is solving: encoding and evaluation. The GA uses a

measure of fitness of individual chromosomes to

carry out reproduction. As reproduction takes place,

the crossover operator exchanges parts of two single

chromosomes, and the mutation operator changes

the gene value in some randomly chosen location of

the chromosome.

The procedure of estimating the hierarchical

variables by GA is summarized as follows:

1. Determine the hierarchical structure and how

many parameters we must find.

2. Construct an initial population randomly.

3. Decode each string in the population

4. Evaluate the fitness value for each string.

5. Reproduce strings according to the fitness value

calculated in Step 4.

6. Go to 3 until the maximum number of iterations

is met.

To start with our algorithm we propose to encode

all parameters in one chromosome. For every

parameter we will dedicate 8 bits, so we can have

the parameters in the range of 2

possibilities. All

the parameters are positive and have one decimal

after the comma, then our range is in [0; 25.6]. The

search space can be changed depending on the

application. Using this simple encoding procedure

we can easily change the number of bits.

Then we evaluate the results using the fitness

function which is based on step response

specifications such as overshoot, rise time and

settling time. We define the fitness function so that it

measures how close each individual in the

population at time t (i.e., each hierarchical

parameter) is to meeting these specification.

Then, after knowing the design specification of

the objective function, and once we can obtain the

step response characteristics for each chromosome

in the population, the fitness function is calculated in

2 steps:

1. We ask if the result coming from the GA is in the

range of design specification of the objective

function. If it is, we go to the step 2. If it is not,

the fitness value of this chromosome is set to 0.

2. The fitness function is defined as

where os is overshoot, ts is settling time and tr is

rising time. The index coef is the specification of the

control problem for which we are looking the

hierarchical parameters. The index dis is the design

specification parameter. In order to minimize the

fitness function we divide 1/FF.

When the evaluation is done, we continue with

the reproduction stage. The new population is

obtained by applying the crossover operator in one

point with probability equal to 0.8 and the mutation

operator with probability equal to 0.1.

5 SIMULATION RESULTS

We applied the proposed method in order to find the

searching parameters. The proposed method was

tested in the inverted pendulum control problem

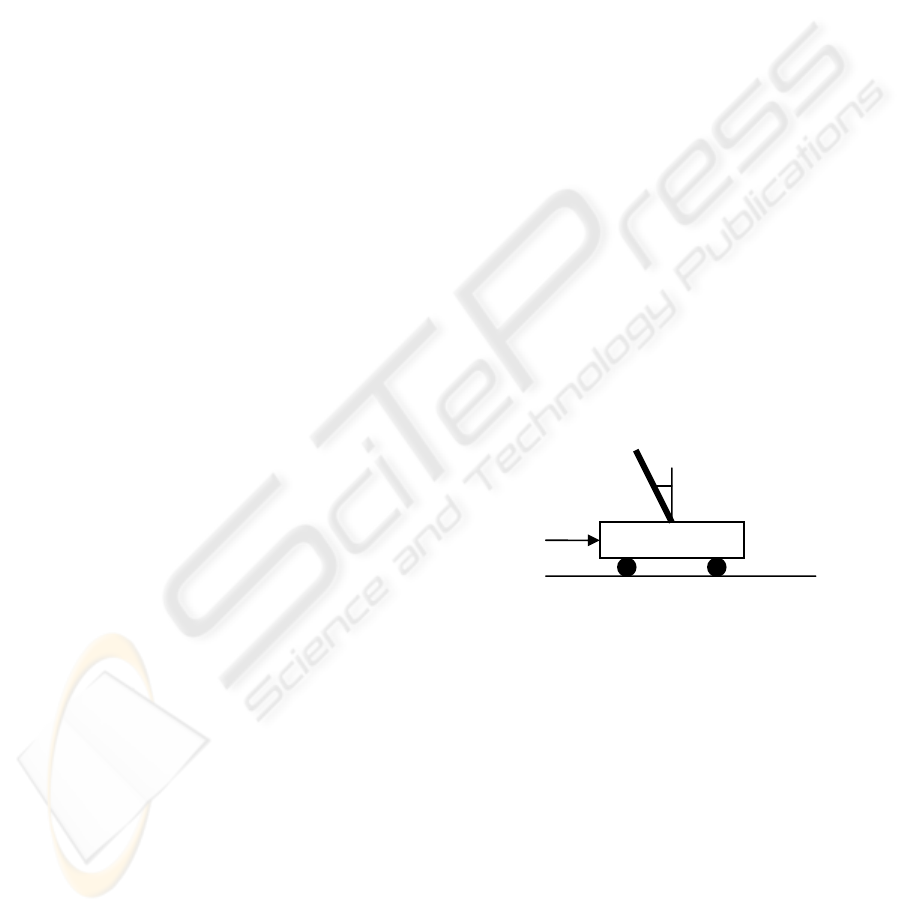
(Nguyen, 2003). This problem consists in the

application of a such power to a cart for not allowing

a pendulum stem to fall down and to carry the cart to

an objective position. The scheme in Figure 2 shows

the main components of the system.

Figure 2: Inverted pendulum.

The basic variables are: angular position of the

stem

, angular velocity of the stem ∆

, horizontal

position of the cart x, and the velocity of the cart ∆x.

The design specifications of the inverted pendulum

system are: objective position of the cart is 30 cm,

overshoot no more than 5%, and settling time no

more than 5 sec.

The simulation of the inverted pendulum is

performed in Simulink of Matlab starting from the

nonlinear equations (Nguyen, 2003). The fuzzy

controllers are implemented in the Matlab’s FIS

Editor. The input fuzzy sets are represented by

triangular membership functions (N, Z and P)

uniformly distributed in the universe of discourse [-

1, 1]. The output fuzzy sets are singletons uniformly

distributed in [-1, 1].

F = (os_coef – os_dis)

+ (ts_coef – ts_dis)

(tr

coe

–tr

dis)

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

400

The fuzzy controller based on hierarchical

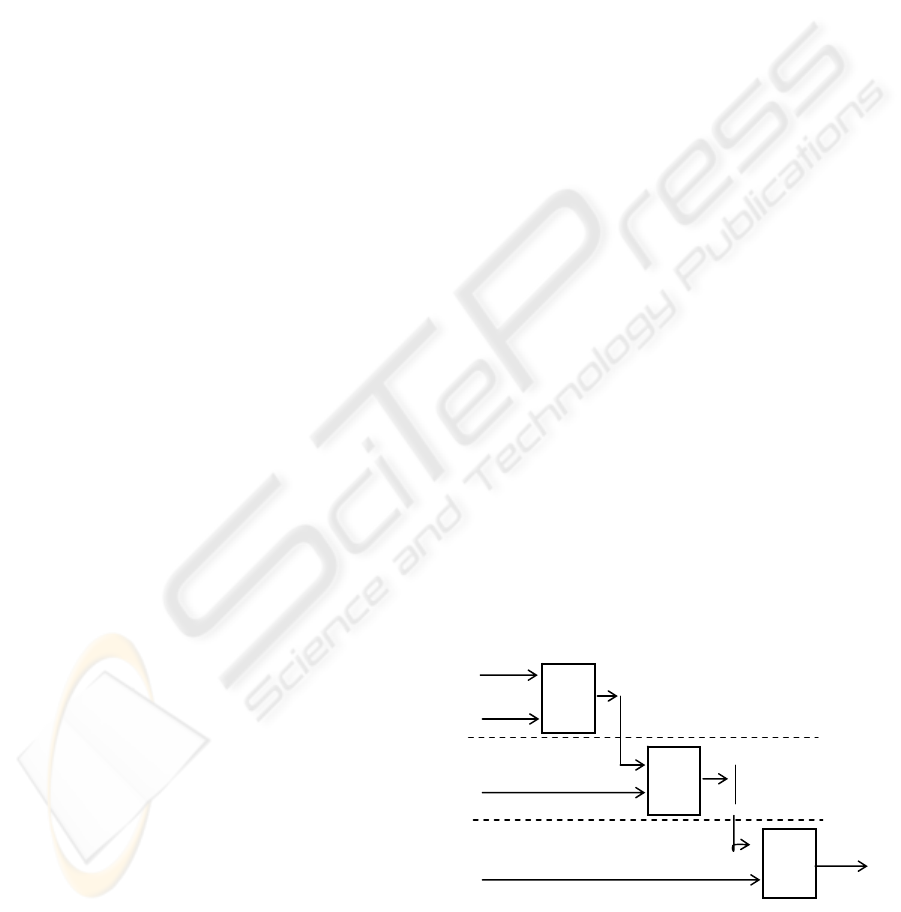
structure is composed of three fuzzy controllers (see

Figure 3). The total number of rules is of 9 for FC1

+ 5 for FC2 + 9 for FC3 = 23 rules.

For applying the reduction with the hierarchical

fuzzy controller method we obtained the following

parameters: a = 19.2, b = 6.4, c = 1.1, and d= 2.3.

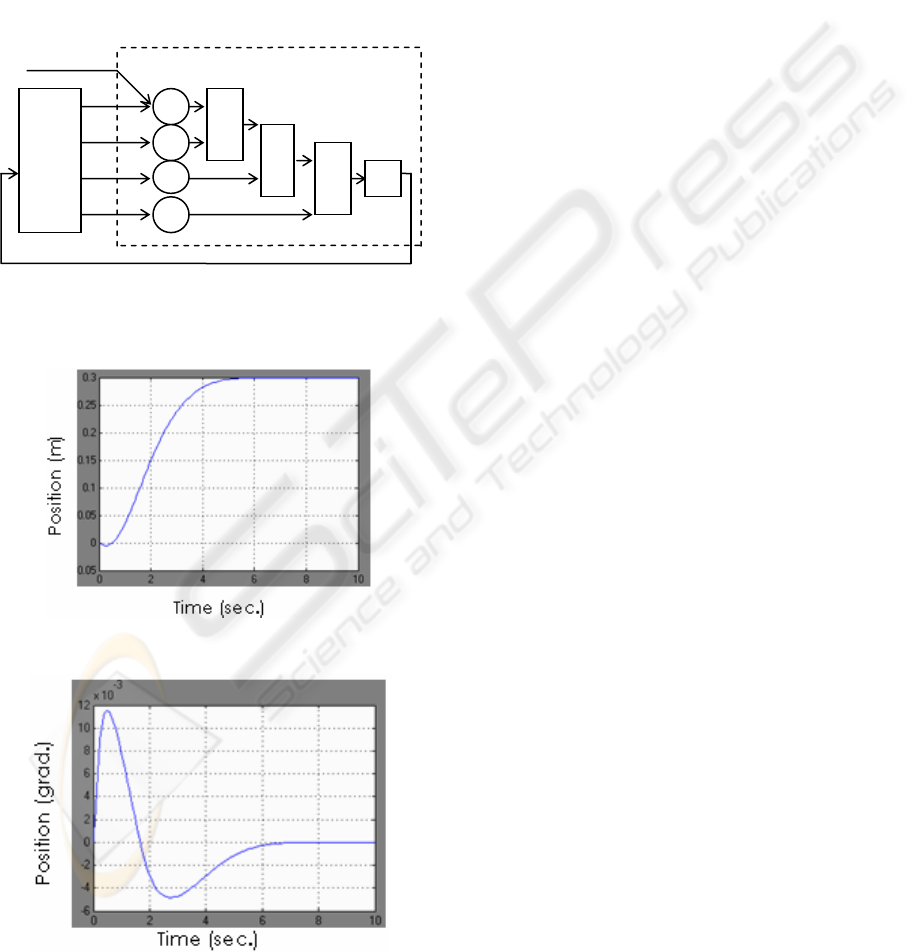
With these parameters, the horizontal position of the

cart is stabilized in 4.69 seconds with overshoot

equal to 0 (see Figure 4), and the behaviour of the

angle position of the stem of pendulum is shown in

Figure 5.

Figure 3: Fuzzy controller based on the hierarchical

structure for inverted pendulum.

Figure 4: Horizontal position of the cart.

Figure 5: Angle position of the stem of pendulum.

6 CONCLUSIONS

The hierarchical structure makes it possible to

significantly reduce the dimensionality of the control

problem. In our approach, the problem of manually

search for the required parameters was solved with

an optimization algorithm (genetic algorithm). The

proposed algorithm was tested by simulation of the

inverted pendulum control problems. The

parameters of the hierarchical method for the design

specifications of this problem were adequately

found.

Due to the fact that the fitness function is based

on the design specification of the system, we have

the advantage to apply it to any combination of

hierarchical variables. Another very important

advantage is that when the user changes the design

specifications, we can obtain the necessary

hierarchical parameters very quickly by using the

proposed GA. GA helped us not only to

automatically estimate the hierarchical parameters,

but also to improve the results obtained by the

hierarchical method.

REFERENCES

Ajith A., 2001. Neuro-Fyzzy Systems: State-of-the-art.

Modeling Techniques. Connectionist Models of

Neurons, Learning Processes, and Artificial

Intelligence. Springer-Verlag, LNCS, Jose Mira and

Alberto Prieto (Eds.), Spain, vol. 2084, pp. 269-276.

Anwer M.J, 2005. A Simple Technique for Generation and

Minimization of Fuzzy Rules. IEEE Conference on

Fuzzy Systems, Nevada.

Bezdek J.C., 1974. Cluster validity with fuzzy sets. J.

Cybern., vol. 3, no.3, pp. 58-71.

Chia-Feng Juang, Chin-Teng Lin, 1998. An On-Line Self-

Constructing Neural Fuzzy Inference Network and Its

Applications. IEEE Transaction on Fuzzy Systems,

vol. 6, No.1, pp. 12-32.

Jamshidi M., 1997. Fuzzy Control Systems. Springer-

Verlag, chapter on Soft Computing, pp. 42-56.

Jang Roger, 1993. ANFIS: Adaptive-Network-Based Fuzzy

Inference Systems. IEEE Trans. System Man &

Cybernetics, vol. 23, pp. 665-685.

Kasabov N., Kozma R., and Duch W., 1998. Rule

Extraction from Linguistic Rule Networks and from

Fuzzy Neural Networks: Propositional versus Fuzzy

Rules. Proc. of NEURAP'98, France, pp. 403-406.

Kim J., Kasabov N, 1999. HyFIS: adaptive Neuro-Fuzzy

Inference Systems and their application to nonlinear

dynamical systems. Neural Networks, 12, pp. 1301-

1319.

Nguyen H.T., Prasad N.R., et al, 2003. A First Course in

Fuzzy and Neural Control. Chapman & Hall/CRC.

∆x

∆Ө

Syste

AUTOMATIC ESTIMATION OF PARAMETERS FOR THE HIERARCHICAL REDUCTION OF RULES OF

COMPLEX FUZZY CONTROLLERS

401