A DUAL MODE ADAPTIVE ROBUST CONTROLLER FOR

DIFFERENTIAL DRIVE TWO ACTUATED WHEELED MOBILE

ROBOT

Samaherni M. Dias, Aldayr D. Araujo

Department of Electrical Engineering, Federal University of Rio Grande do Norte, Brazil

Pablo J. Alsina

Department of Computer Engineering, Federal University of Rio Grande do Norte, Brazil

Keywords:

Variable Structure Systems, Adaptive Control, Decoupling, Nonholonomic Mobile Robot.

Abstract:

This paper is addressed to dynamic control problem of nonholonomic differential wheeled mobile robot. It

presents a dynamic controller to mobile robot, which requires only information of the robot conﬁguration, that

are collected by an absolute positioning system. The control strategy developed uses a linear representation of

mobile robot dynamic model. This linear model is decoupled into two single-input single-output systems, one

to linear displacement and one to angle of robot. For each resulting system is designed a dual-mode adaptive

robust controller, which uses as inputs the reference signals calculated by a kinematic controller. Finally,

simulation results are included to illustrate the performance of the closed loop system.

1 INTRODUCTION

The control of mobile robot is a well known prob-

lem with nonholonomic constraints. There are many

works about it, and several of these works use kine-

matic model. Dynamic model, which is composed by

kinematic model plus the dynamic of robot, is used in

a few works.

An adaptive controller that compensates for cam-

era and mechanical uncertain parameters and ensures

global asymptotic position/orientation tracking was

presented by Dixon (Dixon et al., 2001). Chang

(Chang et al., 2004) proposes a novel way to de-

sign and analysis nonlinear controllers to deal with

the tracking problem of a wheeled mobile robots with

nonholonomic constraints.

The exact mobile robot model is complex and the

model has a lot of parameters to be considered, so

we will use a simpliﬁed model that consider some of

them. But this isn’t the only problem, because some

parameters can suffer variations, as the mass and the

frictional coefﬁcients. For example, when robot is do-

ing a task as to carry an object, the object mass isn’t

considered by the model. So, we are using an associ-

ation between a dual mode adaptive robust controller

(DMARC) and a kinematic controller to the robot lin-

ear model.

The DMARC controller was presented in (Cunha

and Araujo, 2004) and it proposes a connection be-

tween a variable structure model reference adap-

tive controller (VS-MRAC, proposed by Hsu and

Costa(Hsu and Costa, 1989)) and a conventional

model reference adaptive controller (MRAC). The

goal is to have a robust system with fast response and

small oscillations (characteristics of VS-MRAC), and

a smooth steady-state control signal (characteristics

of the MRAC).

2 NONHOLONOMIC MOBILE

ROBOT

The robot considered in this paper is a nonholonomic

direct differential-drive two-actuated-wheeled mobile

robot, which is showed in Fig. 1. The robot is of

symmetric shape and the center of mass is at the geo-

metric center C of the body. It has two driving wheels

ﬁxed to the axis that passes through C. Each wheel is

controlled by one independent motor.

Based on Fig 1, we have that d is distance between

wheels, r

d,e

are right and left wheels radius, ω

d,e

are

right and left wheels angle velocity, ω

is the angle

robot velocity, v

d,e

are right and left wheels linear ve-

M. Dias S., D. Araujo A. and J. Alsina P. (2007).

A DUAL MODE ADAPTIVE ROBUST CONTROLLER FOR DIFFERENTIAL DRIVE TWO ACTUATED WHEELED MOBILE ROBOT.

In Proceedings of the Fourth Inter national Conference on Informatics in Control, Automation and Robotics, pages 39-44

DOI: 10.5220/0001630900390044

 SciTePress

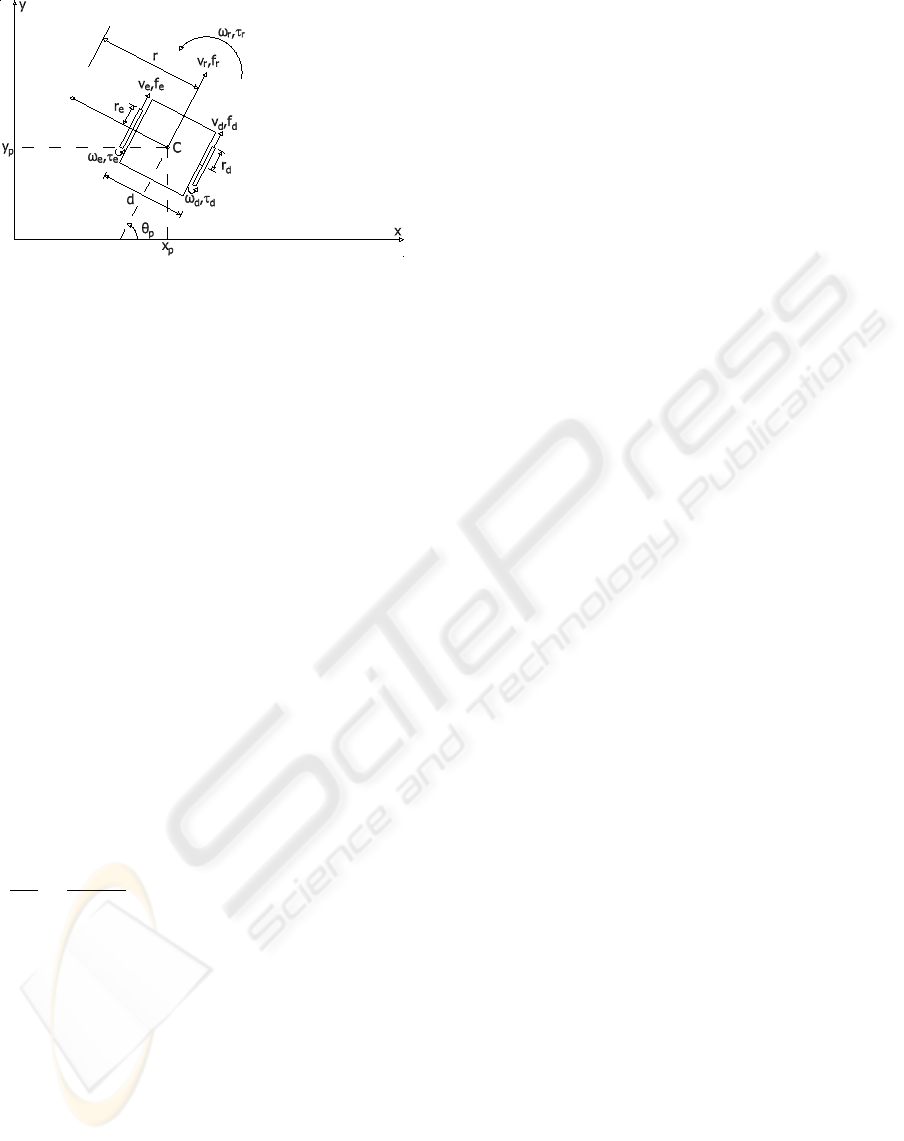
Figure 1: Differential-drive two-actuated-wheeled mobile

robot.

locity, v

is the linear robot velocity, τ

d,e

are right and

left wheels torque, τ

is the robot torque, f

d,e

are right

and left wheels force, f

is the robot force, θ

is the

angle of robot, x

is the x coordinate of C and y

the y coordinate of C.

2.1 Kinematic Model

The robot kinematic is described by equation (1),

˙q =

v (1)

q =













cos(θ

) 0

sin(θ

) 0

0 1





v =





The relation between velocity vectors (ω

and v)

is given by the equation ω

v, with



1/r

d/2r

1/r

−d/2r







This mobile robot has a nonholonomic constraint,

because the driving wheels purely roll and don’t slip.

This constraint is described by

∂y

∂x

sin(θ

)

cos(θ

→ ˙y

cos(θ

) − ˙x

sin(θ

) = 0 (2)

2.2 Dynamic Model

The robot dynamic is represented by the following

equation

f = M

˙v + B

v (3)

which is composed by matrix M

and B

f =







m 0

0 J





lin

0 β

ang



where β

lin

is the frictional coefﬁcient to linear move-

ments, β

ang

is the frictional coefﬁcient to angle move-

ments, m is the robot mass and J is the inertia mo-

ment.

It’s very important to consider the following rela-

tion

f =

τ (4)

with τ is the vector





The DC motors dynamic is obtained of electrical

(5) and mechanical (6) equations,

i = R

e − R

(5)

τ = K

i − J

− B

(6)

where the vectors are

i =







1/R

0 1/R



e =







0 K





0 J





0 β



and e

d,e

are armature motor voltages, R

d,e

are wind-

ings resistances, K

d,e

are constants of induced volt-

age, J

d,e

are inertia moments of rotors, β

d,e

are mo-

tors frictional coefﬁcients and i

d,e

are armature mo-

tors currents.

Using equation (5) in (6) and the result in (4), and

the force f , from (4), in equation (3), gives

= M

˙v + B

v (7)

where

= M

· J

= B

+ B

)

2.3 Linear Representation to Mobile

Robot Dynamic Model

A state-space model, with output vector Y = [S θ

]

is obtained from equation (7) and described by



˙x = Ax + Be

Y = Cx

(8)

where S is the linear displacement and

x =













A =





−M

−1

. 0

2×2

. 0

2×2





B =



−1

2×2



3 INVERSE SYSTEM

The right inverse system is used as an output con-

troller to force the original system output Y (t) to track

a given signal





. The inverse system, in

this paper, is applied to decouple the original MIMO

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

Figure 2: Decoupling based on an inverse system.

(Multiple-Input Multiple-Output) system (8) into two

SISO (Single-input Single-Output) systems (Fig. 2).

To get a stable inverse system, it’s necessary as-

sume that the system discussed is minimum phase.

The inversion algorithm of Hirschorn (Hirschorn,

1979) is applied to decouple the system (8). Deriving

the output vector Y =



S θ



two times the result-

ing system is



˙x = Ax + Be

Y = C

x + D

(9)

where D

is an invertibility matrix, so the inverse sys-

tem is



x =

x +

e =

Y =

x +

A = A − BD

−1

C = −D

−1

B = BD

−1

D = D

−1

u =



0 0 U



= [0

2×2

]

The block diagram in Fig. 2 shows two indepen-

dent systems, which have the same transfer function

(s) = W

(s) = 1/s

obtained by

S,θ

(s) = [C(sI − A)

−1

B] · [

C(sI −

−1

B +

where W

S,θ

(S) =



(s) W

(s)



It’s important to remember that linear displace-

ment (S) is not measurable, so an estimated signal

is used. The linear model and the inverse system

need the exact robot parameters, and we are using

a simpliﬁed model with uncertain parameters. So a

robust adaptive controller will be used to guarantee

a good transient under unknown parameters and dis-

turbances. Two controllers are designed, one to each

transfer function.

4 CONTROLLER STRUCTURE

The controller structure is divided in ﬁve blocks (Fig.

3). First block, which is called kinematic controller,

it will calculate reference values (S

re f

and θ

re f

) based

on desired values (x

,θ

) and absolute position-

ing system (x

,θ

). Second block is composed by

two DMRAC controllers, which are projected to do

the robot to reach reference values. These controllers

based on references values will supply two control

signals (U

and U

) to the inverse system. Third block

is the inverse system, fourth block is the robot and the

ﬁfth block is the estimator.

Figure 3: Controller strategy block diagram.

4.1 Estimator

The linear displacement estimator is given by

S =

∑

sgn(X) ·

i+1

− x

)

+ (y

i+1

− y

)

(10)

where X is

X = x

i+1

cos(θ

) +y

i+1

sin(θ

) −x

cos(θ

) −y

sin(θ

)

So, if X > 0, we have the linear displacement

(

4l > 0) and if X < 0, we have

4l < 0.

4.2 Kinematic Controller

The Fig 4 shows the new variables used in kinematic

controller as ∆l

pos

, that is the distance between robot

and any reference point (x

re f

), ∆λ

pos

is the dis-

tance of robot to point R

pos

that is nearest reference

point in robot orientation axis. φ

pos

is the angle of

robot orientation axis, (∆φ

pos

= φ

pos

− θ

). θ

is de-

sired orientation angle and γ is the difference between

φ and θ

angles (γ = φ − θ

To get that a robot leaves a point and reaches an-

other point it’s necessary ∆l

pos

→ 0 when t → ∞.

Based on decoupled linear model of robot a new

auxiliar point R

pos

(Fig 4) was proposed, to design

a positioning controller, because only in this point

∆λ

pos

= S

re f

− S. So, if ∆λ

pos

→ 0 and ∆φ

pos

→ 0,

the ∆l

pos

→ 0. The reference of DMARC

controller

is calculated by

re f

= ∆l

pos

· cos(∆φ

pos

) + S (11)

and the reference signal to DMARC

controller is

given by

re f

= φ

pos

= tan

−1



re f

− y

re f

− x



(12)

where the equations (11) and (12) represent the po-

sitioning controller and are using only informations

from absolute positioning system.

This work uses a mobile reference system to gen-

erate new points to the positioning controller for each

step of the algorithm. It’s based just in the robot kine-

matic model. The kinematic controller objective is to

A DUAL MODE ADAPTIVE ROBUST CONTROLLER FOR DIFFERENTIAL DRIVE TWO ACTUATED WHEELED

MOBILE ROBOT

Figure 4: Mobile robot coordinates.

do θ

= θ

and ∆l → 0, when t → ∞. For this, we

have to do θ

→ φ

pos

, φ

pos

→ φ and φ → θ

, at the

same time that ∆l → 0 when t → ∞.

Based on the functioning of the positioning con-

troller, it was proposed that each new reference point

has the same distance between robot and desired

point. So

∆l = ∆l

pos

re f

− x

)

+ (y

re f

− y

)

(13)

and that the angle of this point is

tan

−1



re f

− y

re f

− x



= φ + γ (14)

To the equations (13) and (13), we obtain the fol-

lowing equations to positioning controller



re f

= x

+ ∆l · cos(φ +γ)

re f

= y

+ ∆l · sin(φ +γ)

4.3 Dual-Mode Adaptive Robust

Controller

The DMARC uses the compact VS-MRAC structure,

that was proposed by Araujo and Hsu (Araujo and

Hsu, 1990), changing just the last control signal u

(Fig 5) to choose between a VS-MRAC and conven-

tional MRAC controllers.

Consider a linear single-input/single-output time

invariant plant with uncertain parameters and transfer

function,

W (s) = k

(s)

+ α

s + α

with input u and output y. The reference model is

M(s) = k

(s)

+ α

s + α

Figure 5: Block diagram of DMRAC controller with n

∗

= 2.

with input re f and output y

The aim is to ﬁnd u such that the output error

= y − y

tends to zero asymptotically for arbitrary initial con-

ditions and arbitrary piece-wise continuous uniformly

bounded reference signals re f (t).

Following conventional assumptions are made:

1. the plant is observable, controllable, minimum

phase (n

(s) is Hurwitz) and with unknown or un-

certain bounded parameters. d

(s) and n

(s) are

monics polynomials with degree [d

(s)] = 2, de-

gree [n

(s)] = 0 and relative degree n

∗

= 2;

2. the reference model is stable and minimum phase

(s), d

(s) are Hurwitz). d

(s) and n

(s) are

monics polynomials with relative degree known

∗

) ([M(s)] has the same relative degree than

W (s) and signals sgn(k

) = sgn(k

) > 0 (positive,

for simplicity).

3. only input/output measurements are used to ﬁnd

control law u(t).

The following input and output ﬁlters are used



= −λQ

+ gu

= −λQ

+ gy

where Q

∈ ℜ and λ is chosen such that N

(s) is

a factor of det(sI − L). The regressor vector is de-

ﬁned as ω



y Q

re f



, and the control u

is given by

u = Θ

where Θ





is the adaptive

parameter vector.

Considering the above assumptions exists a uni-

que constant vector Θ

∗

, such that the transfer func-

tion of the closed-loop plant W (S), with u = Θ

∗T

ω,

is M(s) (Matching condition). But θ

∗

is obtained of

exact plant parameters. Usually this is not possible

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

in practice, then the Θ is adapted until e

→ 0 when

t → ∞, and eventually (under some signal richness

condition) Θ → Θ

∗

The vector Θ

∗

is obtained as following

∗







(α

− α

)/g

(λ(α

− α

) + (α

− α

) − α

gΘ

∗

)/g

(λ(α

− α

) − α

gΘ

∗

− k

λΘ

∗

)/(k

· g)







The θ

nom

is a nominal value of adaptive parame-

ter vector (ideally, Θ

nom

= Θ

∗

) and it is calculated as

∗

and based on the decoupled plants (W

(s),W

(s))

where α

= α

= 0.

Suppose that exists a polynomial L(s) = (s + δ)

of degree N = 1 where δ > 0 and δ ∈ ℜ such that

M(s)L(s) is SPR (Strictly Positive Real). Consider

the following auxiliary signal (a prediction of the out-

put error e

)

= MLΘ

2n+1

−1

u − Θ

−1

ω]

where Θ

2n+1

and Θ are estimates for 1/Θ

∗

and Θ

∗

(Matching parameters), respectively. The following

augmented error is deﬁned

= (y − y

) − y

= e

− y

Narendra proposes the following modiﬁcation to

guarantee the global stability of the adaptive system

= ML[Θ

2n+1

−1

− Θ

−1

)ω

+αe

−1

ω)

−1

ω)], α > 0

To update Θ and Θ

2n+1

are used the following

adaptive integral laws to MRAC controller

Θ = −e

(L−1ω)

2n+1

= e

(L−1Θ

− Θ

−1

)ω

To VS-MRAC controller, we have to introduce the

following ﬁltered signals ξ

= L

−1

ω, ξ

= ω, χ

−1

u, χ

= u.

The upper bounds are deﬁned by

> |Θ

∗

− Θ

nom,Q1

| Θ

> |Θ

∗

− Θ

nom,n

> |Θ

∗

− Θ

nom,Q2

| Θ

> |Θ

∗

− Θ

nom,2n





0 j

> ρ · Θ

1 j

, j = 1, 2,3,4

κ >



∗

− κ

nom



where ρ = κ

∗

/κ

nom

(ideally ρ = 1) and κ

nom

is a nom-

inal value for k

∗

= 1/Θ

∗

(it is assumed k

nom

6= 0).

Further, it is deﬁned

nom

= Θ

nom

ω (15)

We have plants with n

∗

= 2 and in this case, a VS-

MRAC structure, needs a chain of auxiliary errors to

get the matching condition. The switching laws are

chosen so that the auxiliary errors e

(i = 0,1) become

sliding modes after some ﬁnite time. The equivalent

controls ((u

)

) are, in practice, obtained of (u

) by

means of a low pass ﬁlter (F) with high enough cut-

off frequency.

To adjust the DMARC controller an expression

for the µ parameter, based on the idea of the Takagi-

Sugeno model, was used. This expression is given by

(16), where ` is a parameter to be adjusted.

µ = e

−(e

)

(16)

Notice that when e

→ 0, µ → 1 and the algo-

rithm is the MRAC. When e

becomes reasonably

high, µ assumes a value sufﬁciently small, tending to

the VSMRAC algorithm. The ` parameter has a great

importance in the transition between MRAC and VS-

MRAC. If ` is small the VS-MRAC action will be big.

The DMARC algorithm applied to plants with rel-

ative degree n

∗

= 2 is summarized in the Table 1.

Table 1: Algorithm of DMARC controller.

u = −u

+ u

nom

= κ

nom

ML · [u

− L

−1

]

= e

− y

)

= F

−1

)

= (u

)

− L

−1

)

= κ|χ

− Θ

nom

| + Θ

· |ξ

= Θ

· |ξ

= f

· sgn(e

)

= −Θ

= −αΘ

− αΘ

· sgn(e

ω), α > 0

5 RESULTS

The result showed in this paper is based on simulation

of a micro robot soccer structure. The simulated result

considers the main nonlinearities (see (Laura et al.,

2006)) as dead zone between ±150mV and saturation

to values out of ±10V . It also has noise in input and

output signals. The noise was calculated by a ran-

dom variable with a normal distribution of probabil-

ity. To inputs noises (e

) we have values between

±100mV . To output noises (x

, y

and θ

) we have

values between ±1cm to cartesian points and ±8, 5

to angle.

The unknown parameters are in the dynamic mo-

del, and they are obtained of the exact mobile robot

A DUAL MODE ADAPTIVE ROBUST CONTROLLER FOR DIFFERENTIAL DRIVE TWO ACTUATED WHEELED

MOBILE ROBOT

model with a normal distribution random variable of

probability between 1% and 10%. The parameters

used in the simulation are of a realistic robot, that is

not symmetrical.

A controller DMRAC is applied to each plant

(s) and W

(s) with relative degree → n

∗

= 2).

Choosing a reference model to each plant, we have

(s) =

2.25

+ 3s + 2.25

(s) =

100

+ 20s + 100

and as ﬁlters



= −1.5Q

+ 1.5U

= −1.5Q

+ 1.5S



θ1

= −10Q

θ1

+ 10U

θ2

= −10Q

θ2

+ 10θ

We choose the polynomial L

(s) = s + 1.5 to

DMARC

with F = 22s + 1, `

= 0.7551, α

= 0.05

and

S,nom

= [ −2.0 −6.75 4.5 2.25 ]

S,1

= [ 2.420 13.282 2.657 0.024 ]

We choose the polynomial L

(s) = s + 10 to

DMARC

with F = 56s + 1, `

= 0.0051, α

= 0.05

and

θ,nom

= [ −2.0 −300.0 200.0 9.7 ]

θ,1

= [ 0.073 101.161 175.750 0.1 ]

The Fig. 6 shows a simulation result of the closed

loop system. The robot going from the initial point



0 0 0



to desired point



1 1 0



. When the

robot reaches a circle of 1cm radius with center in de-

sired point, it’s considered that the task was accom-

plished. The controller shows a good transient behav-

ior that means in 3.49s the robot reaches the desired

position without vibrations.

The simulation result is closed to real physical

systems, so it includes the main nonlinearities, a plant

with unknown parameters, bounded disturbances in

the absolute positioning system and in motors driver

system. It uses a sampling interval of 10ms. These

facts did not affect the closed loop system behavior.

In the Fig. 6 is possible identify the functioning

of the DMARC controller. When the error is big a

DMARC operates as VS-MRAC and when the error

is small the DMRAC operates as MRAC.

6 CONCLUSIONS

In this paper a controller that decouples multivariable

system into two monovariable systems was proposed.

For each monovariable system an adaptive robust con-

troller is applied to get desired responses.

The closed loop system with the proposed con-

troller presented a good transient response and robust-

ness to disturbances and errors in the absolute posi-

tioning system and in driver system.

−0.00 0.55 1.10

0.0

0.5

1.0

1.5

Robot Trajectory

Trajectory

Reference Point

0.00 1.75 3.49

−0.82

4.59

10.00

Motors Signals

Right Motor

Left Motor

0.00 1.75 3.49

−0.02

0.77

1.56

X,Y,Angle Evolution

Angle

Figure 6: Robot signals (control signal and output plant).

REFERENCES

Araujo, A. D. and Hsu, L. (1990). Further developments in

variable structure adaptive control based only on in-

put/output measurements. volume 4, pages 293–298.

11th IFAC World Congress.

Chang, C., Huang, C., and Fu, L. (2004). Adaptive track-

ing control of a wheeled mobile robot via uncalibrated

camera system. volume 6, pages 5404–5410. IEEE

International Conference on Systems, Man and Cy-

bernetics.

Cunha, C. D. and Araujo, A. D. (2004). A dual-mode adap-

tive robust controller for plants with arbitrary relative

degree. Proceedings of the 8th International Work-

shop on Variable Structure Systems, Spain.

Dixon, W. E., Dawson, D. M., Zergeroglu, E., and Behal,

A. (2001). Adaptive tracking control of a wheeled

mobile robot via uncalibrated camera system. IEEE

Transactiond on on Systems, Man and Cybernetics,

31(3):341–352.

Hirschorn, R. M. (1979). Invertibility of multivariable non-

linear control systems. IEEE Transactions on Auto-

matic Control, AC-24:855–865.

Hsu, L. and Costa, R. R. (1989). Variable structure model

reference adaptive control using only input and out-

put measurements - part 1. International Journal of

Control, 49(02):399–416.

Laura, T. L., Cerqueira, J. J. F., Paim, C. C., Pomlio, J. A.,

and Madrid, M. K. (2006). Modelo dinmico da es-

trutura de base de robs mveis com incluso de no lin-

earidades - o desenvolvimento do modelo. volume 1,

pages 2879–2884. Anais do XVI Congresso Brasileiro

de Automtica, 2006.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics