REAL-TIME INTER- AND INTRA- CAMERA COLOR MODELING

AND CALIBRATION FOR RESOURCE CONSTRAINED ROBOTIC

PLATFORMS

Walter Nistic

o and Matthias Hebbel

Robotics Research Institute (IRF), Universit

at Dortmund, Otto-Hahn-Str. 8, Dortmund, Germany

Keywords:

Camera modeling, color correction, evolutionary algorithms, real time.

Abstract:

This paper presents an approach to correct chromatic distortion within an image (vignetting) and to compensate

for color response differences among similar cameras which equip a team of robots, based on Evolutionary

Algorithms. Our black-box approach does not make assumptions concerning the physical/geometrical roots

of the distortion, and the efﬁcient implementation is suitable for real time applications on resource constrained

platforms.

1 INTRODUCTION

Robots which base their perception exclusively on vi-

sion, without the help of active sensors such as laser

scanners or sonars, have to deal with severe additional

constraints compared to generic computer vision ap-

plications. The robots have to interact with a dynamic

(and sometimes even competitive or hostile) environ-

ment and must be able to take decisions and react to

unforeseen situations in a fraction of a second, thus

the perception process has to run in real-time with

precise time boundaries. In particular, autonomous

robots are typically constrained even in terms of com-

putational resources, due to limitations in power sup-

ply, size, and cost. A very popular approach espe-

cially for indoor environments is color-based image

segmentation, and even though dynamic approaches

have been demonstrated (for example, (Iocchi, 2007)

(Schulz and Fox, 2004)), static color classiﬁcation

(Bruce et al., 2000) is still the most widely used solu-

tion, due to its efﬁciency and simplicity. In a group of

homogeneous robots, which make use of color infor-

mation in their vision system, it is important that all

cameras produce similar images when observing the

same scene, to avoid to have to individually calibrate

the vision system of each robot, a procedure which is

both time consuming and error prone. Unfortunately,

even when the cameras are from the same model and

produced from the same manufacturer, such assump-

tion does not always hold (R

ofer, 2004).

1.1 The Platform

This work has been developed on the popular Sony

Aibo ERS-7 robot (Sony Corporation, 2004), which is

the only complete standard platform widely adopted

for robotic applications to date. The robot is equipped

with a 576MHz 64bit RISC CPU, 64MB of main

memory, and a low-power CMOS camera sensor with

a maximum resolution of 416 × 320 pixel. Images

are affected by a ring-shaped dark blue cast on the

corners, and different specimen of the same model

tend to produce slightly different color responses to

the same objects and scene. Our experiments have

been conducted using the YUV color space which is

natively provided by most common cameras, but the

approach can be applied unaltered to the RGB color

space. The Aibo production has been recently discon-

tinued by Sony, but several new commercially avail-

able robotic kits are being introduced on the market,

with similar characteristics in terms of size and power,

often equipped with embedded RISC CPUs or PDAs

and low quality compact ﬂash cameras.

1.2 Related Work

Whenever object recognition is mostly based on color

classiﬁcation, the dark / colored cast on the corners of

378

Nisticò W. and Hebbel M. (2007).

REAL-TIME INTER- AND INTRA- CAMERA COLOR MODELING AND CALIBRATION FOR RESOURCE CONSTRAINED ROBOTIC PLATFORMS.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 378-383

DOI: 10.5220/0001631403780383

 SciTePress

the images captured by the on board camera is a se-

rious hindrance. Vignetting is a radial drop of image

brightness caused by partial obstruction of light from

the object space to image space, and is usually de-

pendent on the lens aperture size (Nanda and Cutler,

2001) (Kang and Weiss, 2000). These approaches, as

well as (Manders et al., 2004), treat the problem in

terms of its physical origins due to geometrical de-

fects in the optics, and are mostly focused on radio-

metric calibration, i.e. ensuring that the camera re-

sponse to illumination after the calibration conforms

to the principles of homogeneity and superposition.

However, none of the proposed methods deals with

chromatic distortion, as is the case of our reference

platform, and other inexpensive low power CMOS

sensors. Recently, a few papers have attempted to

tackle such problem. These solutions share a simi-

lar approach to minimize the computational costs by

using lookup tables to perform the correction in real

time, while the expensive calibration of the correc-

tion tables is performed off-line. In (Xu, 2004) the

author uses a model based on a parabolic lens geom-

etry, solved through the use of an electric ﬁeld ap-

proach. No quantitative analysis of the results is pro-

vided, but this technique has been successfully used

in practice by one team of autonomous robots in the

RoboCup Four-Legged League.

Another success-

ful technique used in RoboCup has been presented in

(Nistic

o and R

ofer, 2006), based on a purely black-

box approach where a polynomial correction function

is estimated from sample images using least square

optimization techniques. Since this approach does not

rely on assumptions concerning the physics of the op-

tical system, we feel that it can be more effective in

dealing with digital distortions such as saturation ef-

fects. Again no quantitative analysis has been pre-

sented, and both papers do not address the problem of

inter-robot camera calibration, which has been treated

in (Lam, 2004) with a simple linear transformation of

the color components considered independently.

2 COLOR MODEL

The ﬁrst step to understand the characteristics of this

chromatic distortion, was to capture images of special

cards that we printed with uniform colors, illuminat-

ing them with a light as uniform as possible, trying

to avoid shadows and highlights.

Then we calcu-

RoboCup is an international joint project to promote

AI, robotics, and related ﬁelds. http://www.robocup.org/

However, this is not so critical, and the use of a profes-

sional diffuse illuminator is not necessary, as our approach

can deal well with noise and disturbances (see Section 2.1).

lated the histograms of the three image spectra, with

a number of bins equal to the number of possible val-

ues that each spectrum can assume, i.e. 256. Under

these conditions, the histograms of such uniform im-

ages should be uni-modal and exhibit a very narrow

distribution around the mode (in the ideal case, such

distribution should have zero variance, i.e. all the pix-

els have exactly the same color) due only to random

noise. Instead, it could be observed that the variance

of the distribution is a function of the color itself; in

case of the U channel, it appears very narrow for cold

/ bluish color cards, and very wide for warm / yel-

lowish cards (Figure 1(a)). Consequently, we model

the chromatic distortion d

for a given spectrum i of a

given color I as a function of I

itself, which here we

will call brightness component λ

(a) (b)

Figure 1: a) Histograms of the U color band for uniformly

colored images: yellow, green and skyblue. Notice how the

dispersion (due to the vignetting) increases inverse propor-

tionally to the position of the mode. b) Brightness distri-

bution of the U color band for a uniformly yellow colored

image.

The distribution itself is not centered around the

mode, but tends to concentrate mostly on one side

of it. The reason for this becomes apparent by ob-

serving the spatial distribution of the error (cf. Fig-

ure 1(b)); the phenomenon itself is nothing but a ring

shaped blue/dark cast, whose intensity increases pro-

portionally to the distance from the center of the dis-

tortion (u

, v

), which lies approximately around the

optical center of the image, the principal point. So,

let r =

(x − u

)

+ (y − v

)

, then we deﬁne

the radial component as ρ

(r(x, y)). Putting together

brightness and radial components, we obtain our dis-

tortion model:

(I(x, y)) ∝ ρ

(r(x, y)) · λ

(x, y)) (1)

Now, due to the difﬁculty to analytically derive

, λ

, ∀i ∈ {Y, U, V } about which little is known,

we decided to use a black-box optimization ap-

proach. Both sets of functions are non-linear, and we

chose to approximate them with polynomial functions

REAL-TIME INTER- AND INTRA- CAMERA COLOR MODELING AND CALIBRATION FOR RESOURCE

CONSTRAINED ROBOTIC PLATFORMS

379

(McLaurin series expansion).

(r) =

j=0

i,j

· r

) =

j=0

i,j

· I

(2)

The unknown polynomial coefﬁcients %

i,j

and l

i,j

can

be estimated, from a set of samples, using naturally

inspired machine learning techniques. So, the ﬁnal

vignetting correction function is as follows:

(x, y) = I

(x, y) − ρ

(r(x, y)) · λ

(x, y)) (3)

where I

(x, y) is the corrected value of the spectrum

i of the given pixel.

2.1 Reference Color Estimation

To be able to model our error functions, we must

ﬁrst estimate how the pictures should look like, if

they were not affected by any chromatic distortion.

Since most of the image area exhibits little to no dis-

tortion, we deﬁne as reference color of a single im-

age the most frequent color appearing in its spec-

tra. So we calculate the histograms of the 3 color

spectra (number of bins = number of color levels =

256) and we ﬁnd the modes ¯r

, ¯r

, which repre-

sent the reference color for image i. However, a sin-

gle image can be affected by other sources of noise,

such as a temporary change of light intensity, strob-

ing (aliasing between the camera shutter speed and

the light source power frequency, which affects ﬂu-

orescent lights) or shadows: consequently, the his-

tograms’ modes might have temporary ﬂuctuations,

or exhibit multiple nearby modes. To make our sys-

tem more robust toward this kind of noise, we col-

lect multiple pictures of each colored cards in a log

ﬁle, and we partition the images therein contained

into image classes

, where a class represents a cer-

tain color card (e.g. yellow, orange, green, blue) at

a certain light intensity and camera settings. For each

image class j we want to have a single reference color

: of course this could be obtained by av-

eraging the references from all the images which be-

long to the class, but this would still be affected by

outliers. Instead, we track the current reference of a

given class using a simple ﬁrst order linear Kalman

ﬁlter (Welch and Bishop, 2003):

• For each image i in the log, a reference value is es-

timated for the 3 spectra ¯r

, ¯r

, as the modal

value of the corresponding histogram

With image class or color class here we will refer to

a color card captured under certain lighting settings, i.e.

the same color card can be represented by different color

classes, like blue-dark and blue-light.

• Constant value process model: the predicted ref-

erence color

for class j at the fol-

lowing step (image i) remains the same as the one

after the measurement update of image i − 1

• We use the output of the Kalman ﬁlter to perform

the partitioning into color classes on the ﬂy; a new

class is generated when:

∃c ∈ {Y, U, V } :



− ¯r



> ϑ (4)

where ϑ is a conﬁdence threshold; so if at least

one of the spectra in the reference of the current

image differs too much from the expected refer-

ence for the current class, then we need to create

a new color class. A new class reference is initial-

ized to the value extracted from the current image.

• Measurement model: we update the running class

reference

using the reference ex-

tracted from the current image

2.2 Inter-camera Model

In the general case, it is possible that to completely

correct the difference in color response between two

cameras it is necessary to rotate the color space of one

camera to align with the other. This however, is not

feasible for a real time implementation for robotic ap-

plications. To capture the dependencies between the

3 color components and the distance from the image

center, we would need a 256

· ρ

max

look-up table,

which would have a size of over 2GB even for our

low resolution camera. Otherwise, we could perform

the rotation with the multiplication of a 3 × 3 ma-

trix by our color vector; since such costly operation

would have to be performed for every pixel, it would

slow down the image processing too much.

In (Lam, 2004) the author suggests a simple linear

transformation of the 3 color components of the cam-

era to be calibrated, treating them independently from

each other; such an approach is used in image pro-

cessing programs to perform adjustments in the color

temperature of a picture. Since we are going to use

an evolutionary approach to the optimization process,

we have decided to give more freedom to the inter-

camera transformation, by using higher order polyno-

mials instead:

(x, y) = A

(x, y)) =

j=0

i,j

· (I

(x, y))

(5)

(x, y) is the i-th color component of pixel x, y of

the camera that we want to calibrate, a

i,j

are the

transformation coefﬁcients which have to be learned,

and I

(x, y) is the resulting value, for a certain color

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

380

spectrum i ∈ {Y, U, V }, which should match the

color as it would appear if taken by the camera of the

reference (“alpha”) robot. Further, we must obtain I

from I

by applying the vignetting correction as de-

scribed. All robots in the team have to be calibrated

to match the color representation of the “alpha” robot,

hence each robot will have its own set of coefﬁcients

i,j

When different cameras exhibit similar vignetting

characteristics, the vignetting correction polynomials

can be calculated only once for all cameras, then the

inter-camera calibration can be performed indepen-

dently and using much less sample images. In fact,

in our experiments we have seen that learning both

polynomial sets at the same time can easily lead to

over-ﬁtting problems, with the inter-camera calibra-

tion polynomials which also end up contributing to

compensate the vignetting distortion (for example by

clipping the high and low components of the color

spectra), but this results in a poor generalization to

the colors which are out of the training set.

2.3 Realtime Execution

After optimizing off-line the parameters %

i,j

, l

i,j

, a

i,j

with the techniques presented in Section 3, we are

able to calculate the corrected pixel color values

, U

, V

), given the uncorrected ones (Y, U, V )

and the pixels’ position in the image (x, y). Perform-

ing the polynomial calculations for all the pixels in

an image is an extremely time-consuming operation,

but it can be efﬁciently implemented with Look-Up

Tables:

• radialLU T[x, y] =

(x − u

)

+ (y − v

)

stores the pre-computed values of the distance of

all the pixels in an image from the center of dis-

tortion (u

, v

);

• colorLU T [r, l, i] = A

(l − ρ

(r) · λ

(l)) where

r = radialLUT [x, y], l = I

(x, y) ∈ [0 . . . 255]

and i ∈ {Y, U, V } is the color spectrum. We ﬁll

the table for all the possible values of r, l, c, the

size of the table is 256 · r

max

· 3 elements, so it

occupies only ≈ 200KBytes in our case

The look-up tables are ﬁlled when the robot is booted;

afterward it is possible to correct the color of a pixel

in real-time by performing just 2 look-up operations.

3 PARAMETER OPTIMIZATION

The goal is to ﬁnd an “optimal” parameter set for the

described color model given a set of calibration im-

ages as previously described. Thus, we consider as

optimal the parameter set which minimizes the “func-

tion value” (from now on referred to as ﬁtness), de-

ﬁned as the sum of squared differences of the pixels

in an image from the reference value calculated for

the color class in which the image belongs. To calcu-

late the ﬁtness of a certain parameter set, given a log

ﬁle of images of colored cards, we proceed as follows:

• For each image I

i,k

in the log ﬁle (i is the color

band, k the frame number), given its reference

value previously estimated R

i,k

, the current ﬁt-

ness F

is calculated as:

(x,y )



i,k

(x, y) − R

i,k



(6)

• The total ﬁtness F

is calculated as the sum of the

where each k is an image which belong to a

different color class; this to ensure that the ﬁnal

parameters will perform well across a wide spec-

trum of colors and lighting situations, which oth-

erwise might only ﬁt a very speciﬁc situation.

The optimization process is performed independently

for each color band i ∈ {Y, U, V }. To optimize the

vignetting correction, we use for A() (from Equation

5) the identity function, and the references R

i,k

which

are extracted from the same log (and same robot) that

we are using for the optimization process. In case

of inter-robot calibration instead, only A

() will be

optimized, ρ

(), λ

() will be ﬁxed to the best func-

tions found to correct the vignetting effect, and the

references R

i,k

are extracted from a log ﬁle gener-

ated from another (“alpha”) robot, which is used as

reference for the calibration. If we want to opti-

mize the center of distortion (u

, v

), we need a set

of ρ

(), λ

() calculated in a previous evolution run

as ﬁtness for this process we use the sum of the ﬁt-

nesses of all 3 color channels, under the assumption

that there is only one center of distortion for all color

bands.

3.1 Simulated Annealing (SA)

In Simulated Annealing (Kirkpatrick et al., 1983) in

each step the current solution is replaced by a random

“nearby” solution, chosen with a probability that de-

pends on the corresponding function value (“Energy”)

and on the annealing temperature T . The current so-

lution can easily move “uphill” when T is high (thus

jumping out of local minima), but goes almost ex-

clusively “downhill” as T approaches zero. In our

work we have implemented SA as follows (Nistic

and R

ofer, 2006).

Otherwise, changing u

, v

would have no effect on

the ﬁtness

REAL-TIME INTER- AND INTRA- CAMERA COLOR MODELING AND CALIBRATION FOR RESOURCE

CONSTRAINED ROBOTIC PLATFORMS

381

In each step, the coefﬁcients %

i,j

, l

i,j

(vignetting

reduction) or a

i,j

(inter-robot calibration) or (u

, v

)

(center of distortion) are “mutated” by the addition of

zero mean gaussian noise, the variance of which is

dependent on the order of the coefﬁcients, such that

high order coefﬁcients have increasingly smaller vari-

ances (decreasing order of magnitude) than low order

ones, following the idea that small changes in the high

order coefﬁcients produce big changes in the overall

function. The mutated coefﬁcients are used to correct

the image, as in Equation 5.

For each image I

i,k

in the log ﬁle (i is the color

spectrum, k the frame number), given its reference

value previously estimated R

i,k

, the current “energy”

E for the annealing process is calculated as in Equa-

tion 6. The “temperature” T of the annealing is low-

ered using a linear law, in a number of steps which

is given as a parameter to the algorithm to control

the amount of time spent in the optimization process.

The starting temperature is normalized relative to the

initial energy, so that repeating the annealing process

on already optimized parameters has still the possi-

bility to perform “uphill moves” and ﬁnd other opti-

mum regions. The process ends when the tempera-

ture reaches zero; the best parameters found (lowest

energy) are retained as result of the optimization pro-

cess.

This approach has proved to work well with our

application, however it has 2 shortcomings:

• The search space is very irregular and has mul-

tiple local and even global optima. One reason

for the latter is that the function to be optimized

is the product of different terms (ρ

() · λ

()), so

that exactly the same result can be achieved by

multiplying one term by a factor and the other by

its reciprocal, or inverting the sign for both terms,

etc.

• The variances used to mutate the coefﬁcients give

a strong bias to the ﬁnal results, as it is not possi-

ble to fully explore such a wide search space in a

reasonable time; the depicted approach lacks the

ability to ﬁnd “good” mutation parameters, apart

from the simple heuristic of decreasing the vari-

ance order at the increase of the coefﬁcient order

Both issues can be dealt with efﬁciently by Evolution

Strategies.

3.2 Evolution Strategies (ES)

Evolution Strategies (Schwefel, 1995) use a parent

population of µ ≥ 1 individuals which generate

λ ≥ 1 offsprings by recombination and mutation.

ES with self-adaption additionally improve the con-

trol of the mutation strength: each parameter which

has to be optimized (object parameter) is associated

with its own mutation strength (strategy parameter).

These strategy parameters are also included in the en-

coding of each individual and are selected and inher-

ited together with the individual’s assignments for the

object parameters.

An offspring is created by recombination of the

parents. We use two parents to generate an offspring,

then such offsprings are subject to mutation.

The selection operator selects the parents for the

next generation based on their ﬁtness. In case of the

(µ, λ)-strategy only the best µ individuals out of the

offsprings are chosen to be the parents of the next gen-

eration. Our implementation works similarly as the

annealing process, with the following exceptions:

• (µ, λ) strategy with self-adaption, the strategy pa-

rameters are initialized with the same sigmas used

in the annealing process;

• We terminate the evolution process when n gen-

erations have passed without any ﬁtness improve-

ment

Having µ > 1 means that several different “optimal”

areas of the search space can be searched in parallel,

while the self-adaptation should make the result less

dependent from the initial mutation variances.

4 EXPERIMENTS AND RESULTS

At ﬁrst we compared the two optimization techniques

to see what is most suitable for our application. We

ran the optimization on a log ﬁle containing 9 image

classes, the evolution strategy used 8 parents and 60

offsprings, stopping the evolution after 10 generations

without improvements. For simulated annealing, we

set the number of steps to match the number of ﬁtness

evaluations after which ES aborted, ≈ 5000; the total

optimization time, for both algorithms, is around 5

minutes, on a 1.7GHz Pentium-M CPU. As it can be

seen in Figure 2, both algorithms signiﬁcantly reduce

the image error, but ES found better optima than SA;

the results of these techniques are affected by random

factors, however except for extremely low evolution

times (< 1min), ES outperforms SA consistently.

To test the performance of our approach for inter-

robot calibration, we created 2 log ﬁles containing im-

ages representing 6 different color cards taken from

2 robots (one of which we use as reference and call

“alpha robot”) which show a very different color re-

sponse, especially for the yellow and pink cards. Ta-

ble 1 shows that the optimization succeeded in reduc-

ing the error standard deviation often by a factor of

3 or more, as well as shifting the modes of the im-

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

382

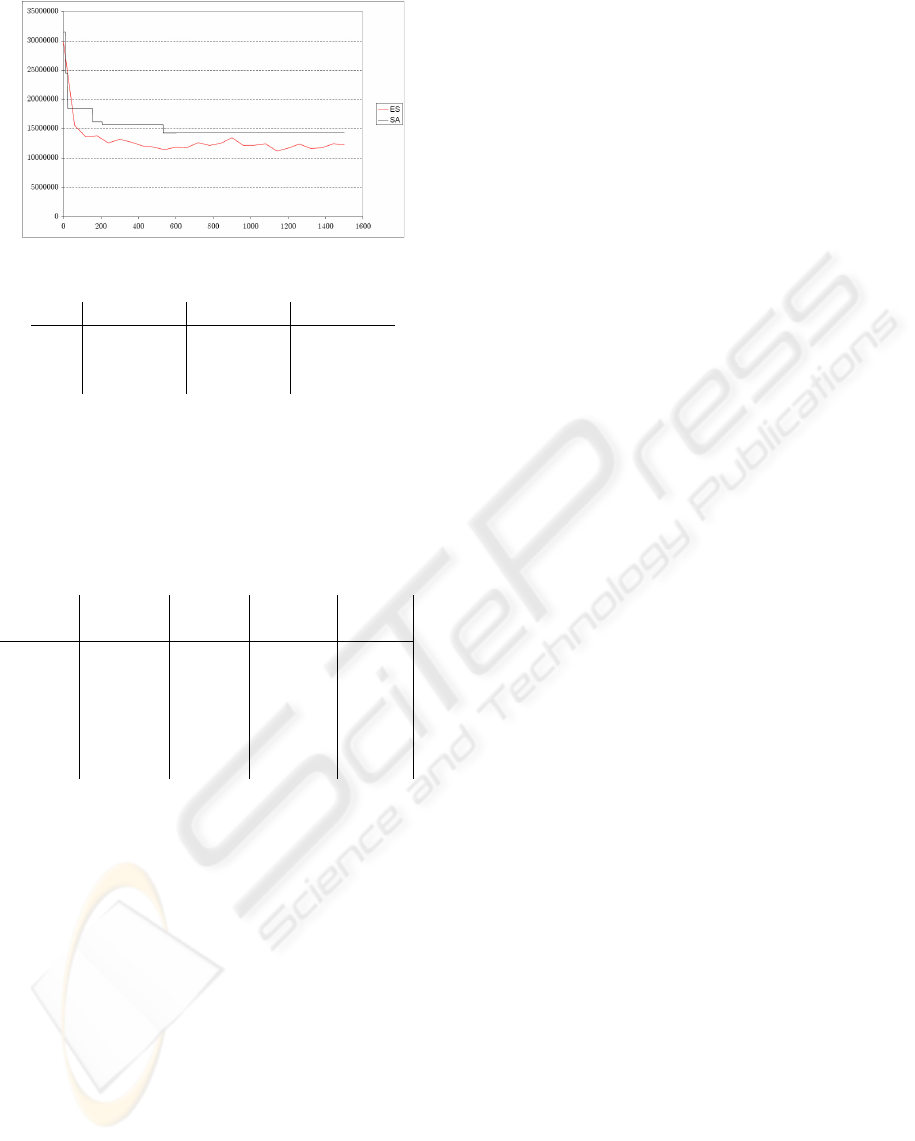
(a) The ﬁtness curves for the correction of the U-

channel.

Y U V

init 49677830 31517024 53538715

SA 23608403 14298870 16127666

ES 20240155 10819027 15581825

(b) The initial and achieved best ﬁtnesses.

Figure 2: Results of the vignetting reduction.

Table 1: Inter-robot calibration. ∆µ

start

, ∆µ

end

represent

the difference of the mode of the robot from the reference

(“alpha”) before and after the calibration. σ

start

, σ

end

are

the standard deviation from the reference mode.

Color ∆µ

start

∆µ

end

start

end

Card Y/U/V Y/U/V Y/U/V Y/U/V

green 1/0/3 1/0/4 6.2/3.8/7.4 3.2/3.0/3.9

orange 18/12/5 7/2/3 13.3/17.8/9.3 4.6/4.8/4.2

cyan 13/2/8 5/2/4 11.3/3.9/4.8 4.4/3.8/4.0

red 4/9/5 2/1/1 7.6/15.2/7.5 3.1/5.2/3.6

yellow 6/7/30 5/4/5 21.5/8.3/24.8 6.0/3.9/5.5

pink 17/6/5 3/1/2 24.6/12.6/8.9 5.3/4.3/5.6

ages much closer to the reference values provided by

the alpha robot. The total optimization time, split in

2 runs (one for the vignetting, the other for the inter-

robot calibration) was approximately 6 minutes.

5 CONCLUSIONS

We have presented a technique to correct chromatic

distortion within an image and to compensate for

color response differences among similar cameras

which equip a team of robots. Since our black-box ap-

proach does not use assumptions concerning the phys-

ical/geometrical roots of the distortion, this approach

can be easily applied to a wide range of camera sen-

sors and can partially deal with some digital sources

of distortion such as clipping / saturation. Its efﬁcient

implementation has a negligible run-time cost, requir-

ing just two look-up operations per pixel, so it is suit-

able for real time applications on resource constrained

platforms.

REFERENCES

Bruce, J., Balch, T., and Veloso, M. (2000). Fast and

inexpensive color image segmentation for interactive

robots. In Proceedings of the 2000 IEEE/RSJ Interna-

tional Conference on Intelligent Robots and Systems

(IROS ’00), volume 3, pages 2061–2066.

Iocchi, L. (2007). Robust color segmentation through adap-

tive color distribution transformation. In RoboCup

2006: Robot Soccer World Cup X, Lecture Notes in

Artiﬁcial Intelligence. Springer.

Kang, S. B. and Weiss, R. S. (2000). Can we calibrate a

camera using an image of a ﬂat, textureless lambertian

surface? In ECCV ’00: Proceedings of the 6th Euro-

pean Conference on Computer Vision-Part II, pages

640–653. Springer-Verlag.

Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983). Op-

timization by simulated annealing. Science, Number

4598, 13 May 1983, 220, 4598:671–680.

Lam, D. C. K. (2004). Visual object recognition using sony

four-legged robots. Master’s thesis, The University

of New South Wales, School of Computer Science &

Engineering.

Manders, C., Aimone, C., and Mann, S. (2004). Camera

response function recovery from different illumina-

tions of identical subject matter. In IEEE International

Conference on Image Processing 2004.

Nanda, H. and Cutler, R. (2001). Practical calibrations for

a real-time digital omnidirectional camera. Technical

report, CVPR 2001 Technical Sketch.

Nistic

o, W. and R

ofer, T. (2006). Improving percept reli-

ability in the sony four-legged league. In RoboCup

2005: Robot Soccer World Cup IX, Lecture Notes in

Artiﬁcial Intelligence, pages 545–552. Springer.

ofer, T. (2004). Quality of ers-7 camera images.

http://www.informatik.uni-bremen.de/˜roefer/ers7/.

Schulz, D. and Fox, D. (2004). Bayesian color estimation

for adaptive vision-based robot localization. In Pro-

ceedings of IROS.

Schwefel, H.-P. (1995). Evolution and Optimum Seeking.

Sixth-Generation Computer Technology. Wiley Inter-

science, New York.

Sony Corporation (2004). OPEN-R SDK Model Informa-

tion for ERS-7. Sony Corporation.

Welch, G. and Bishop, G. (2003). An introduction to the

kalman ﬁlter.

Xu, J. (2004). Low level vision. Master’s thesis, The Uni-

versity of New South Wales, School of Computer Sci-

ence & Engineering.

REAL-TIME INTER- AND INTRA- CAMERA COLOR MODELING AND CALIBRATION FOR RESOURCE

CONSTRAINED ROBOTIC PLATFORMS

383