
ON THE FORCE/POSTURE CONTROL OF A CONSTRAINED
SUBMARINE ROBOT
Ernesto Olgu
´
ın-D
´
ıaz and Vicente Parra-Vega
Robotics and Advanced Manufacturing, CINVESTAV-IPN, Saltillo, M
´
exico
Keywords:
Underwater vehicles, Force/position control, Sliding Modes Control.
Abstract:
An advanced, yet simple, controller for submarine robots is proposed to achieve simultaneously tracking of
time-varying contact force and posture, without any knowledge of its dynamic parameters. Structural proper-
ties of the submarine robot dynamic are used to design passivity-based controllers. A representative simulation
study provides additional insight into the closed-loop dynamic properties for regulation and tracking cases. A
succinct discussion about inherent properties of the open-loop and closed-loop systems finishes this work.
1 INTRODUCTION
In the last decade, we have witness a surprising leap
on scientific knowledge and technological achieve-
ments for submarine robots, from a simple torpedo
to modern UAV. Those vehicles are at the same time
tantamount scientific and technological challenges to
robotics, control and mechatronic researchers. First
efforts for free motion submarine robots were focused
for motion control, with sensing capabilities, similar
to the case of fix-base robots in our labs. Of course,
stable contact for submarine robots is a more com-
plex problem in comparison to the typical force con-
trol problem of robot manipulators fixed to ground be-
cause not only due complementary complex dynam-
ics such as buoyancy and added masses, but to de fact
that the vehicle reference frame is not longer inertial.
However, some tasks requires more challeng-
ing goal of establishing stable contact, which leads
us to study the problem of simultaneous force and
pose (position and orientation) control of submarine
robots. When the submarine robot achieves contact,
like pushing itself against a wall or polishing a sunken
surface vessel or manipulating tools on submarine
pipe lines, forces are presented, and little is known
about these contact forces, let alone exploit them ei-
ther for design or control. The main general reason
that this problem remains rather open is that we really
know so little about, on one hand, in how to model and
control properly a fully immersed vehicle constrained
by rigid object; and on the other hand, the submarine
force control technology lies behind system require-
ments, such as very fast sampling rates, even when
the bandwidth of the submarine robot is very low.
Despite brilliant control schemes for free motion
submarine robots in the past few years, in particular
those of (Yoerger, 1985; Smallwood, 2001; Small-
wood, 2004) those schemes does not guarantee for-
mally convergence of tracking errors, let alone si-
multaneous convergence of posture and contact force
tracking errors, there are several results that suggest
empirically that a simple PD control structure be-
haves as stiffness control for submarine robots. So far
the simultaneous convergence of time-varying contact
forces and posture remains an open problem for the
PD-like controller (notice that for submarine robots
the role of model-free controllers are very important
because it is very hard to known exactly the dynamic
model and its dynamic parameters).
Recently, some efforts have focused on how to
obtain simple control structures to control the time-
varying pose of the UAV under the assumption that
the relative velocities are low. For force control, vir-
tually none complete control system has been pub-
lished. However, to move forward more complex
force controllers, we believe that more understanding
of the structural properties of submarine robots in sta-
ble contact to rigid objects are required.
19
Olguín-Díaz E. and Parra-Vega V. (2007).
ON THE FORCE/POSTURE CONTROL OF A CONSTRAINED SUBMARINE ROBOT.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 19-28
DOI: 10.5220/0001631800190028
Copyright
c
SciTePress

To understand more about this problem, we show
that the open-loop rigid dynamics of submarine robots
subject to holonomic constraints (rigid contact) ex-
hibits similar properties of fixed-base robots. Then
almost any force/position control scheme with the
proper adequation can be used. In this paper we
have chosen the orthogonalization principle (Parra-
Vega and Arimoto, 1996) to propose a simple con-
troller with advanced tracking stability properties.
1.1 Contribution
Despite the complexity of the problem, in this pa-
per, the performance of a robot submarine carry-
ing out a very simple contact tasks under a novel
orthogonalization-based model-free controller is an-
alyzed and discussed, with emphasize on structural
properties. The closed-loop shows robust tracking of
time-varying contact force and posture, without any
knowledge of submarine dynamics. The proposed
controller stands itself as a new controller which guar-
antees simultaneous tracking of submarine robot with
a model-free decentralized control structure.
1.2 Organization
Section 2 introduces the nonlinear differential alge-
braic equations of the robot submarine dynamics in
error coordinates. Section 3 presents the control de-
sign. Simulation data is presented for a Testbed robot
of IFREMER in 4, and finally section 5 discusses
some structural properties useful for further under-
stand robot submarine in contact tasks. Conclusions
are stated in Section 6.
2 THE MODEL
2.1 A Free Floating Submarine
The model of a submarine can be obtained via Kirch-
hoff formulation (Fossen, 1994), the inclusion of hy-
drodynamic effects such as added mass, friction and
buoyancy and the account of external forces/torques
like contact effects (Olgu
´
ın-D
´
ıaz, 1999). The model
is then expressed by the next set of equations:
M
v
˙
ν+C
v
(ν)ν+ D
v
(·)ν+ g
v
(q) = u+ F
(v)
c
(1)
ν = J
ν
(q)˙q (2)
From this set, (1) is called the dynamic equation while
(2) is called the kinematic equation. Both had been
used long widely to express the dynamical behavior
of free moving object in the 3D space.
The generalized coordinates vector q ∈ IR
6
is
given on one hand by the 3 Cartesian positions x, y,z
of the origin of the submarine frame (Σ
v
) with respect
to a inertial frame (Σ
0
) fixed in some place on the sur-
face of the Earth; and on the other hand by any set of
attitude parameters that represent the rotation of the
vehicle’s frame with respect to the inertial one. Most
common sets of attitude representation such a Euler
angles, in particular roll-pitch-yaw (φ, θ,ψ), use only
3 variables (which is the minimal number of orien-
tation variables). Then, for a submarine vehicle, the
generalized coordinates q = (x
v
,y
v
,z
v
,φ
v
,θ
v
,ψ
v
) rep-
resents its 6 degrees of freedom.
The vehicle’s velocity ν ∈ IR
6
is the vector repre-
senting both linear and angular velocity of the subma-
rine expressed in its own vehicle’s frame. This vector
is then defined as ν = (v
(v)
v
T
,ω
(v)
v
T
)
T
. The relation-
ship between this vector and the generalized coordi-
nates is given by the kinematic equation. The linear
operator J
ν
(q) ∈ IR
6×6
in (2) is built by the concate-
nation of two transformations. The first is defined as:
J
q
(q) =
I 0
0 J
θ
(φ
v
,θ
v
,ψ
v
)
∈ IR
6×6
Where J
θ
∈ IR
3×3
is an operator that converts
time derivatives of attitude (orientation) parameters
in angular velocity: ω
(0)
v
= J
θ
(θ
v
)
˙
θ
v
, with θ
v
=
(φ
v
,θ
v
,ψ
v
)
T
defined as the orientation parameter vec-
tor. The operator J
q
(q) maps the first time derivative
of the generalized coordinates to linear and angular
velocities of the submarine vehicle, both expressed in
the inertial frame Σ
0
.
The second operator transforms a 6 dimension
tensor from the inertial frame to vehicle’s frame by
J
R
(q) = diag{R
v
0
,R
v
0
} ∈ IR
6×6
. Thus the Jacobian of
the vehicle used in the kinematic equation is a linear
operator defined as:
J
ν
(q) = J
T
R
(q)J
q
(q)
In the dynamic equation (1), matrices
M
v
,C
v
(ν),D
v
(·) ∈ IR
6×6
are respectively Inertia
matrix, Coriolis matrix and Damping matrix. M
v
includes the terms of classical inertia plus the hydro-
dynamic coefficients of the added mass effect (due
to the amount of extra energy needed to displace the
surrounding water when the submarine is moving).
This Inertia matrix is constant, definite positive and
symmetric only when the submarine is complete
immersed and the relative water incidence velocity is
small (Fossen, 1994). This condition is met for most
common activities of a ROV, for example during
sampling recollection in not shallow waters. The
Coriolis vector C
v
(ν)ν represents the Coriolis forces,
gyroscopic terms of the classical inertia effects plus
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
20

the quadratic velocity terms induced by the added
mass. The Coriolis matrix in this representation
does not depend on the position but only on the
velocity, in contrast to the same expression for a
Robot Manipulator (Spong M.W., 1989). However
it fulfills the classic relationship for Lagrangian
systems:
˙
M
v
− 2C
v
(ν) = Q; Q + Q
T
= 0, and is
indeed skew symmetric. The Damping matrix
represents all the hydrodynamic effects of energy
dissipation. For that reason it is a strictly positive
definite matrix, D
v
(q,ν,t) > 0 (Fossen, 1994). Its
arguments are commonly the vehicle’s orientation
φ
v
,θ
v
,ψ
v
, the generalized velocity ν, and the velocity
of the surrounding water. The diagonal components
represents the drag forces while the off-diagonal
components represent the lift forces.
Finally, vectors g
v
(q),u,F
(v)
c
∈ IR
6
are all force
wrenches (force-torque vector) in the vehicle’s frame.
They represent respectively: gravity, input control
and the contact force. Gravity vector includes buoy-
ancy effects and it does not depend on velocity but
on the orientation (attitude) of the submarine with re-
spect to the inertial frame. The contact force wrench
is the one applied by the environment to the subma-
rine. The input control are the forces/torques induced
by the submarine thrusters in the vehicle frame.
The dynamic model (1)-(2) can be rearranged by
replacing (2) and its time derivative into (1). The re-
sult is one single equation model:
M
q
(q)¨q+C
q
(q, ˙q)˙q+ D
q
(·)˙q+ g
q
(q) = u
q
+ τ
c
(3)
which has the form of any Lagrangian system. Its
components fulfills all properties of such systems i.e.
definite positiveness of inertia and damping matrices,
skew symmetry of Coriolis matrix and appropriate
bound of all components (Sagatun, 1991).
The control input in this equation is obtained by a
linear transformation of the real input using the linear
operator given by the kinematic equation:
u
q
= J
T
ν
(q)u. (4)
This last equation becomes important because it re-
lates the nominal control signal u
q
to be designed in
the general coordinates space with the real physical
input u that shall be implemented in the real vessel.
The contact effect is also obtained by the same trans-
formation. However it can be expressed directly from
the contact wrench in the inertial frame (Σ
0
) by the
next relationship
τ
c
= J
T
ν
(q)F
(v)
c
= J
T
q
(q)F
(0)
c
(5)
where the contact force F
(0)
c
is the one expressed in
the inertial frame. By simplicity it will be noted
as F
c
from this point further. The relationship with
the one expressed in the vehicle’s frame is given by
F
c
= J
T
R
(q)F
(v)
c
. This wrench represents the contact
forces/torques exerted by the environment to the sub-
marine as if measured in a non moving (inrtial) frame.
These forces/torques are given by the normal force of
an holonomic constraint when in contact and the fric-
tion due to the same contact. For simplicity in this
work, tangential friction is not considered.
2.2 Contact Force Due to a Holonomic
Constraint
A holonomic constraint can be expressed as a function
of the generalized coordinates of the submarine as
ϕ(q) = 0 (6)
with ϕ(q) ∈ IR
r
. The number r stand for the num-
ber of contact points between the submarine and the
motionless rigid object. Stable contact appears only
when the robot submarine does not deattach from the
object modeled by ϕ(q) = 0. In this case, the time
derivatives of this constraint are zero
d
n
ϕ(q)
dt
n
= 0; ∀ n ≥ 1 (7)
For n = 1 the last constraint becomes:
˙
ϕ(q) = J
ϕ
(q)˙q = 0 (8)
where J
ϕ
(q) =
∂ϕ(q)
∂q
∈ IR
r×n
is the constraint jaco-
bian. Last equation means that velocities of the sub-
marine in the directions of constraint jacobian are re-
stricted to be zero. This directions are then normal to
the constraint surface ϕ(q) at the contact point. As
a consequence, the normal component of the contact
force has exactly the same direction as those defined
by J
ϕ
(q). Then the contact force wrench can be ex-
pressed as
F
c
= J
T
ϕ+
(q)λ (9)
where J
ϕ+
(q)
△
=
J
ϕ
kJ
ϕ
k
is a normalized version of the
constraint jacobian; and λ is the magnitude of the
normal contact force at the origin of vehicle frame:
λ = kF
c
k.
The free moving model expressed by (1)-(2),
when in contact with the holonomic constraint can be
rewritten as:
M
v
˙
ν+ h
v
(q,ν,t) = u+ J
T
R
(q)J
T
ϕ+
(q)λ (10)
ν = J
ν
(q)˙q (11)
ϕ(q) = 0 (12)
where h
v
(q,ν,t) = C
v
(ν)ν+ D
v
(q,ν,t)ν + g
v
(q).
ON THE FORCE/POSTURE CONTROL OF A CONSTRAINED SUBMARINE ROBOT
21

Equivalently, the model (3) is also expressed as
M
q
(q)¨q+ h
q
(q, ˙q,t) = u
q
+ J
T
¯
ϕ
(q)λ (13)
ϕ(q) = 0 (14)
with h
q
(q, ˙q,t) = C
q
(q, ˙q)˙q+ D
q
(q, ˙q,t)˙q+ g
q
(q) and
J
¯
ϕ
(q) = J
ϕ+
(q)J
q
(q). Equations (13)-(14) are a set
of Differential Algebraic Equations index 2 (DAE-2).
To solve them numerically, a DAE solver is required.
This last representation has the same structure and
properties as those reported in (Parra-Vega, 2001).
2.3 Numerical Considerations
To compute the value of λ, the constrained La-
grangian that fulfils the constrained movement, can be
calculated using the second derivative of (7):
¨
ϕ(q) =
0. Then using the dynamic equation (either of them)
and after some algebra its expression becomes either:
λ =
h
J
ϕ
J
−1
ν
M
−1
v
J
T
R
J
T
ϕ+
i
−1
J
ϕ
J
−1
ν
M
−1
v
h
v
− u
−
d
dt
J
ϕ
J
−1
ν
ν
(15)
=
h
J
ϕ
M
−1
q
J
T
¯
ϕ
i
−1
J
ϕ
M
−1
q
(h
q
− u
q
) −
˙
J
ϕ
˙q
(16)
The set of equations (10)-(11)-(15) or the set (13)-
(16) describes the constrained motion of the subma-
rine when in contact to infinitely rigid surface de-
scribed by (6). Numerical solutions of these sets can
be obtained by simulation, however the numerical so-
lution, using a DAE solver, can take too much effort
to converge due to the fact that these sets of equa-
tion represent a highly stiff system. In order to min-
imize this numerical drawback, the holonomic con-
straint has been treated as a numerically compliant
surface which dynamic is represented by
¨
ϕ(q) + D
˙
ϕ(q) + Pϕ(q) = 0 (17)
This is known in the force control literature of robot
manipulators as constrained stabilization method,
which bounds the nonlinear numerical error of in-
tegration of the backward integration differentiation
formula. With a appropriate choice of parameters
P ≫ 1 and D ≫ 1, the solution of ϕ(q,t) → 0 is
bounded. This dynamic is chosen to be fast enough to
allow the numerical method to work properly. In this
way, it is allowed very small deviation on the com-
putation of λ, typically in the order of −10
6
or less,
which may produce, according to some experimental
comparison, less than 0.001% numerical error. Then,
the value of the normal contact force magnitude be-
comes:
λ =
h
J
ϕ
J
−1
ν
M
−1
v
J
T
R
J
T
ϕ+
i
−1
J
ϕ
J
−1
ν
M
−1
v
h
v
− u
−
d
dt
J
ϕ
J
−1
ν
ν− DJ
ϕ
J
−1
ν
ν− Pϕ(q)
(18)
=
h
J
ϕ
M
−1
q
J
T
¯
ϕ
i
−1
J
ϕ
M
−1
q
(h
q
− u
q
) −
˙
J
ϕ
˙q
−DJ
ϕ
˙q− Pϕ(q)
(19)
It can be pointed out that equation (19) compute the
contact force magnitude using the generalized coor-
dinates variables only. From this equation, desired
force can be easily obtained. Also note that the pre-
liminary inverse operator is only expressed by the in-
ertia matrix inverse and the two constraint jacobians.
The first is the gradient of the contact surface, while
the second is the normalized gradient with a simple
kinematic variation given by the operator J
q
.
3 CONTROL DESIGN
The introduction of a so called Orthogonalization
Principle has been a key in solving, in a wide sense,
the force control problem of a robot manipulators.
This physical-based principle states that the projec-
tion (dot product) of contact forces and joint gener-
alized velocities is zero. Then passivity arises from
torque input to generalized velocities. To preserve
passivity, then, the closed-loop system must satisfy
the passivity inequality for controlled generalized er-
ror velocities. This is true for robot manipulators with
fixed frame, and here we prove that this also hap-
pens with robot whose reference frame is not inertial
(fixed).
3.1 Orthogonalization Principle and
Linear Parametrization
Similar to (Liu et al., 1997), an orthogonal projection
of J
ϕ
(q) arises onto the tangent space at the contact
point. This tangent space can be calculated by the
definition of the following operator
Q(q)
△
= I
n
− J
T
ϕ
(q)J
ϕ
(q) ∈ IR
n×n
(20)
where I
n
is an identity matrix of proper size. No-
tice that rank{Q(q)} = n− r since rank{J
ϕ
(q)} = r.
Also notice that Q˙q = ˙q due to the definition of Q and
(8). Therefore, and according to the Orthogonaliza-
tion Principle the integral of (τ, ˙q) is upper bounded
by −
H (t
0
), for H (t) = K + P, and passivity arise
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
22

for fully immersed submarines without inertial frame.
Therefore, passivity-based control is a powerful op-
tion to control such systems.
On the other hand it is known that equation (13)
can be linearly parameterized as follows
M
q
(q)¨q+C
q
(q, ˙q)˙q+ D
q
(·)˙q+ g
q
(q) = Y(q, ˙q, ¨q)Θ
(21)
where the regressor Y(q, ˙q, ¨q) ∈ IR
n×p
is composed
of known nonlinear functions and Θ ∈ IR
p
by p un-
known but constant parameters.
3.2 Change of Coordinates
A variation Y
r
of regressor Y can be designed such
that
Y
r
(q, ˙q, ˙q
r
, ¨q
r
)Θ = (22)
M
q
(q)¨q
r
+ [C
q
(q, ˙q) + D
q
(·)] ˙q
r
+ g
q
(q)
where ( ˙q
r
, ¨q
r
) are some time functions yet to be de-
fined. Then the open loop equation (13) can be written
by adding and subtracting (22) as
M
q
(q)˙s = −[C
q
(q, ˙q) + D
q
(·)]s (23)
−Y
r
(q, ˙q, ˙q
r
, ¨q
r
)Θ+ J
T
¯
ϕ
(q)λ+ u
q
where s
△
= ˙q − ˙q
r
is called the extended error. The
problem of control design for the open loop equation
(23) is to find u
q
such that exponential convergence
arises when Y
r
Θ is not available.
3.3 Orthogonal Nominal Reference
Consider that q
d
(t) and λ
d
(t) are the desired trajecto-
ries functions for position and contact force. Consider
as well, the tracking errors defined as ˜q
△
= q(t) − q
d
(t)
for position error while
˜
λ
△
= λ(t) − λ
d
(t) stand for the
force contact error. Consider also the next set of defi-
nitions:
S
p
△
=
˙
˜q+ σ˜q (24)
S
dp
△
= S
p
(t
0
)e
−α(t−t
0
)
(25)
S
qp
△
= S
p
− S
dp
(26)
S
F
△
=
t
t
0
˜
λdt (27)
S
dF
△
= S
F
(t
0
)e
−η(t−t0)
(28)
S
qF
△
= S
F
− S
dF
(29)
with α > 0, η > 0. Finally, consider the following
reference ˙q
r
function:
˙q
r
= Q
˙q
d
− σ˜q+ S
dp
− γ
1
t
t
0
sgn{S
qp
(t)}dt
(30)
+βJ
T
ϕ
S
F
− S
dF
+ γ
2
t
t
0
sgn{S
qF
(t)}dt
where the parameters β, σ, γ
1
and γ
2
are constant ma-
trices of appropriate dimensions; and sgn(y) stands
for the entrywise signum function of vector y,
Using (30) into s, it arises
s = Q(q)S
vp
− βJ
T
ϕ
(q)S
vF
(31)
where the orthogonal extended position and force
manifolds S
vp
and S
vF
, respectively, are given by
S
vp
= S
qp
+ γ
1
sgn(S
qp
(ς))dς (32)
S
vF
= S
qF
+ γ
2
sgn(S
qF
(ς))dς (33)
Notice that although the time derivative of ˙q
r
is
discontinuous, it will not be used in the controller.
In the next subsection we show that if
˙
S
vp
,
˙
S
vF
are
bounded, and for large enough γ
1
,γ
2
, then simultane-
ous tracking of contact force and posture is achieve.
3.4 Model-Free Second Order Sliding
Mode Control
Consider the following nominal continuous control
law:
u
q
= −K
d
Q(q)s
vq
− βJ
T
ϕ
(q)s
vF
(34)
+J
T
¯
ϕ
(q)
−λ
d
+ S
F
+γ
2
J
T
¯
ϕ
(q)
tanh(µS
qF
) + η
sgn(S
qF
)
with µ > 0 and K
d
= K
T
d
> 0,∈ IR
n×n
. This nominal
control, designed in the q-space can be mapped to the
original coordinates model, expressed by the set (1)-
(2), using the next relationship
u = J
−T
ν
(q)u
q
(35)
thus, the physical controller u is implemented in terms
of a key inverse mapping J
−T
ν
.
3.4.1 Closed-loop System
The open loop system (23) under the continuous
model-free second order sliding mode control (34)
yields to
M
q
˙s = −[C
q
+ D
q
+ K
d
]s−Y
r
Θ (36)
+J
T
¯
ϕ
˜
λ+ ηS
F
+ γ
2
J
T
¯
ϕ
Z + τ
∗
+γ
2
J
T
¯
ϕ
sgn(S
qF
) + η
sgn(S
qF
)
ON THE FORCE/POSTURE CONTROL OF A CONSTRAINED SUBMARINE ROBOT
23

where Z = tanh(µS
qF
) − sgn(S
qF
) and τ
∗
≡ 0 is the
virtual control input for the passivity analysis.
3.4.2 Stability Analysis
Theorem 1 Consider a constrained submarine (13)-
(16) under the continuous model-free second order
sliding mode control (34). The Underwater system
yields a second order sliding mode regime with local
exponential convergence for the position, and force
tracking errors.
Proof. A passivity analysis hS, τ
∗
i indicates that
the following candidate Lyapunov function V quali-
fies as a Lyapunov function
V =
1
2
(s
T
M
q
s+ βS
T
vF
S
vF
) (37)
for a scalar β > 0. The time derivative of the Lya-
punov candidate equation immediately leads to
˙
V = −s
T
(K
d
+ D
q
)s− βηS
T
vF
S
vF
− s
T
Y
r
Θ
+s
T
γ
2
J
T
¯
ϕ
Z (38)
≤ −s
T
K
d
s− βηS
T
vF
S
vF
+ kskkY
r
Θk
+kskkγ
2
kkJ
¯
ϕ
kkZk
≤ −s
T
K
d
s− βηS
T
vF
S
vF
+ kskkεk
where it has been used the skew symmetric property
of
˙
M − 2C(q, ˙q), the boundedness of both the feed-
back gains and submarine dynamic equation (there
exists upper bounds for M,C(q, ˙q),g(q), ˙q
r
, ¨q
r
), the
smoothness of ϕ(q) (so there exists upper bounds for
J
ϕ
and Q(q)), and finally the boundedness of Z. All
these arguments establish the existence of the func-
tional ε. Then, if K
d
, β and η are large enough such
that s converges into a neighborhood defined by ε cen-
tered in the equilibrium s = 0, namely
s → ε as t → ∞ (39)
This result stands for local stability of s provided that
the state is near the desired trajectories for any initial
condition. This boundedness in the
L
∞
sense, leads to
the existence of the constants ε
3
> 0 and ε
4
> 0 such
that
|
˙
S
vp
| < ε
3
, (40)
|
˙
S
vF
| < ε
4
(41)
An sketch of the local convergence of S
vp
is as fol-
lows
1
. Locally, in the n − r dimensional image of Q,
we have that S
∗
qp
= QS
qp
∈ IR
n
. Consider now that un-
der an abuse of notation that S
qp
= S
∗
qp
, such that for
1
The strict analysis follows Liu, et. al.
small initial conditions, if we multiply the derivative
of S
qp
in (32) by S
T
qp
, we obtain
S
T
qp
˙
S
qp
= −γ
1
|S
qp
| + S
T
qp
˙
S
vp
(42)
≤ −γ
1
|S
qp
| + |S
qp
||
˙
S
vp
|
Substituting (40) into (42) yields
S
T
qp
˙
S
qp
≤ −(γ
1
− ε
3
)|S
qp
| (43)
where γ
1
must be chosen such that γ
1
> ε
3
. The equa-
tion (43) is precisely the condition for the existence of
a sliding mode at S
qp
(t) = 0. The sliding mode is es-
tablished in a time t ≤ |S
qp
(t
0
)|/(γ
1
−ε
3
), and accord-
ing to the definition of S
qp
(below (32)), S
qp
(t
0
) = 0,
which simply means that S
qp
(t) = 0 for all time. We
see that if we multiply the derivative of (33) by S
T
vf
,
we obtain
S
T
qF
˙
S
qF
= −γ
2
|S
qF
| + S
T
qF
˙
S
vF
(44)
≤ −γ
2
|S
qF
| + |S
qF
||
˙
S
vF
|
substituting (41) into (44) yields
S
T
qf
˙
S
qf
≤ −(γ
2
− ε
4
)|S
qf
| (45)
where γ
2
must be chosen such that γ
2
> ε
4
. The equa-
tion (45) is precisely the condition for the existence
of a sliding mode at S
qF
(t) = 0. The sliding mode
is established in a time t ≤ |S
qF
(t
0
)|/(γ
2
− ε
4
) and,
according to (33), S
qF
(t
0
) = 0, which simply means
that S
qf
(t) = 0 for all time, which simply implies that
λ → λ
d
exponentially fast.
4 SIMULATION RESULTS
Force control of submarine robots is in its infancy,
therefore simulations study must be kept rather simple
to enter into the intricacies of the numerical solutions.
Later on, the complexity of the simulation study will
be be increased such that underwater disturbances can
include unmodelled submarine dynamics, such as lat-
eral marine current with high Reynolds number, to
mention one. Then, the simulation study has been
made on a simplified platform of a real submarine.
Data has been obtained from the Vortex system of
IFREMER (IFREMER, 1992). Simulator presents
only vertical planar results (only in the x-z plane), so
the generalized coordinates for this case of study are:
q =
x
v
z
v
θ
v
(46)
The vehicle velocities are
v =
u
v
w
v
q
v
(47)
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
24
where u
v
and w
v
are linear velocities (surge and
heave) and q
v
is the angular velocity in the x-z plane.
The holonomic constraint is given by a vertical sur-
face located at 2 meters from the origin. This is ex-
pressed as:
ϕ(q) ≡ x− 2 (48)
Initial conditions were calculated to be at the con-
tact surface with no force. Simulations with simple
PD were also performed as a comparison tool. The
model-free control parameters are as follows:
α β γ
1
γ
2
4 0.025 0.0025 10
−3
K
d
σ η µ
200
ˆ
M
v
5 1000 1
where
ˆ
M
v
is made by the diagonal values of the con-
stant Inertia matrix when expressed in the vehicle’s
frame. For de PD the gains were defined as K
p
=
100
ˆ
M
v
and K
d
= 20
ˆ
M
v
. The numerical dynamic in-
duced in the constraint surface were performed with
P = 9x10
6
and D = 36x10
3
.
4.1 Set-Point Control Case
The task is very simple. It consist on a change of deep,
from 1m to 1.5m, and orientation from 5 degrees to 0,
while the submarine remains in contact with a con-
stant contact force of 170N.
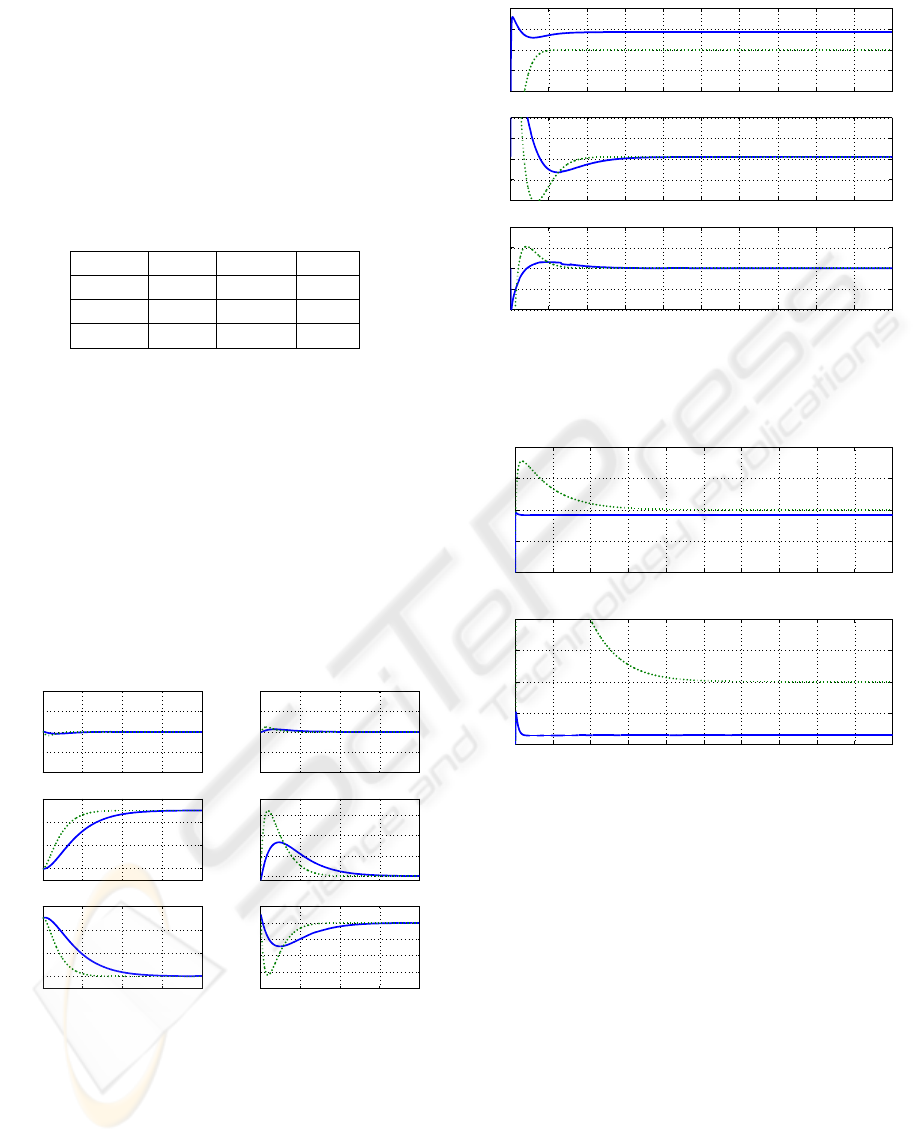
0 0.5 1 1.5 2
1.99
1.995
2
2.005
2.01
x position [m]
0 0.5 1 1.5 2
−1
−0.5
0
0.5
1
Surge (u
v
) [m/s]
0 0.5 1 1.5 2
1
1.2
1.4
1.6
Deep [m]
0 0.5 1 1.5 2
0
0.5
1
1.5
Heave (w
v
) [m/s]
0 0.5 1 1.5 2
0
2
4
6
time [sec]
Orientation [deg]
0 0.5 1 1.5 2
−0.4
−0.3
−0.2
−0.1
0
0.1
time [sec]
Angular velocity [rad/s]
Figure 1: Generalized coordinates q and vehicle velocities
ν, in vehicle’s frame (continuous line for model-free second
order sliding mode control, dotted line for PD control).
Figures 1 and 2 shows respectively position, ve-
locity and force inputs. The difference in settling time
has been explicitly computed in order to visualize the
qualitative differences. In any case, this time inter-
val can be modified with appropriate tuning of gain
parameters. Notice that there is some transient and
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
−400
−200
0
200
400
Input force on x [N]
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
−400
−200
0
200
400
Input force on z [N]
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
−40
−20
0
20
40
time [sec]
Input torque [Nm]
Figure 2: Inputs controlled forces u, in vehicle’s frame (con-
tinuous line for model-free second order sliding mode con-
trol, dotted line for PD control).
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
−2000
−1000
0
1000
2000
Contact force [N]
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
−200
−100
0
100
200
time [sec]
Contact force (detail) [N]
Figure 3: Contact force magnitude λ (continuous line for
model-free second order sliding mode control, dotted line
for PD control).
variability in the position of the contact point in the
the direction normal to that force (the x coordinate).
This is more visible in the velocity curve where veloc-
ity in the x direction should not occur if the constraint
is infinitely rigid. The same transients are present in
the force graphic where a noticeable difference be-
tween simple PD and model-free second order sliding
mode control is present. The big difference is that al-
though PD can regulate with some practical relative
accuracy it is not capable to control force references,
either constant nor variable. Figure 3 shows the tran-
sient of the contact force magnitude λ (only the 1st
second is shown). The second window shows with
more detail the transient in this contact force due to
the numerical modification. In this graphic is is clear
that no force is induced with the PD scheme. In the
ON THE FORCE/POSTURE CONTROL OF A CONSTRAINED SUBMARINE ROBOT
25
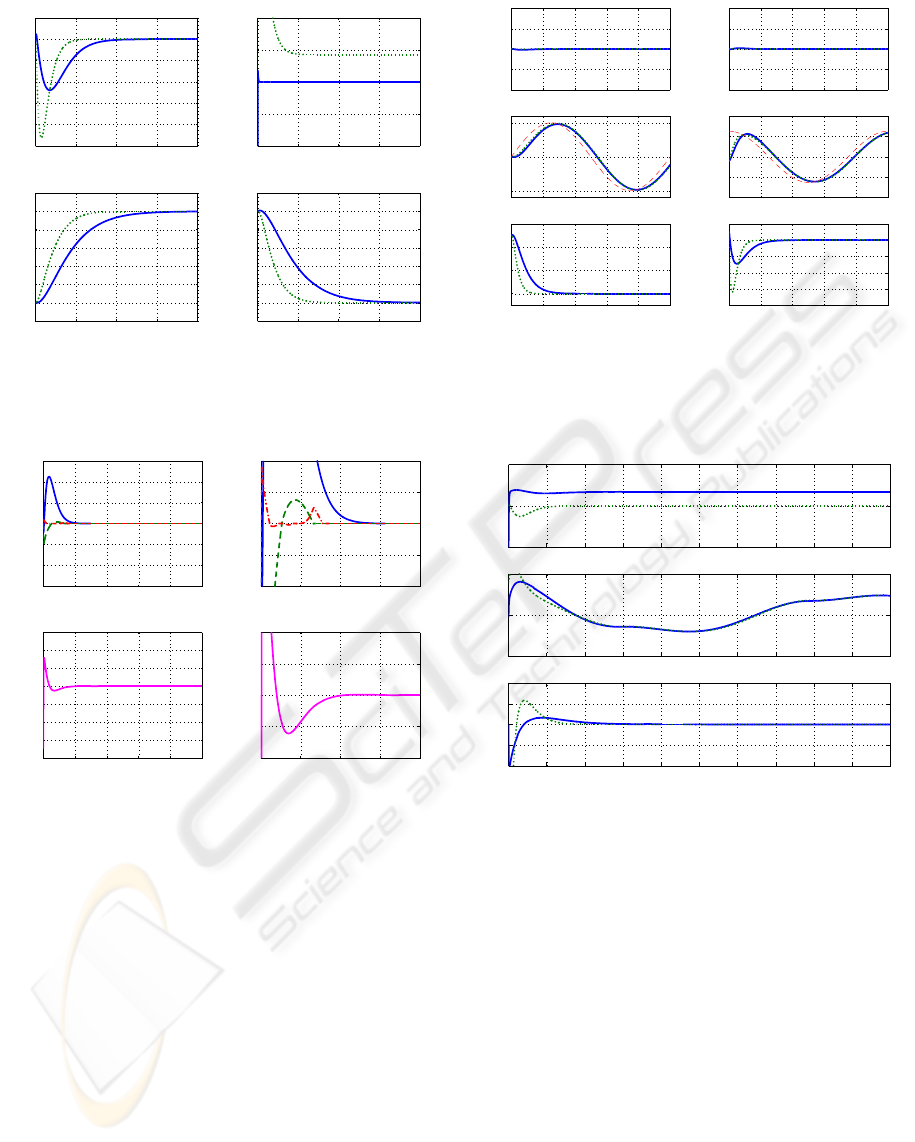
0 0.5 1 1.5 2
−10
−8
−6
−4
−2
0
2
x 10
−4
x error [m]
0 0.5 1 1.5 2
−400
−200
0
200
400
Force contac error [N]
0 0.5 1 1.5 2
−0.5
−0.4
−0.3
−0.2
−0.1
0
0.1
time [sec]
Deep error [m]
0 0.5 1 1.5 2
−1
0
1
2
3
4
5
time [sec]
Orientation error [deg]
Figure 4: Set-point control errors: ˜q = q(t) − q
d
and
˜
λ =
λ(t)− λ
d
(continuous line for model-free second order slid-
ing mode control, dotted line for PD control).
0 1 2 3 4 5
−0.1
−0.05
0
0.05
0.1
0.15
S
qp
0 0.5 1 1.5 2
−0.01
−0.005
0
0.005
0.01
0 1 2 3 4 5
−0.4
−0.3
−0.2
−0.1
0
0.1
0.2
0.3
time [sec]
S
qF
0 0.5 1 1.5 2
−0.04
−0.02
0
0.02
0.04
time [sec]
Figure 5: Control variables S
qp
and S
qF
for the model-free
second order sliding mode control.
case of the model-free 2nd order sliding mode, force
set-point control is achieved very fast indeed. Fig-
ure 4 shows the set-point control error for position (3
curves) and force. Is again evident the substantial dif-
ference in schemes for force control. Figure 5 shows
the convergence of the extended position and force
manifolds. They do converge to zero and induce there
after the sliding mode dynamics.
4.2 Tracking Control Case
This task differs from the set-point control case in that
the deep is a periodic desired trajectory center at 1
meter deep with 1 meter amplitude (pick to pick) and
a 5 sec period. Contact desired force remains constant
at 170N.
0 1 2 3 4 5
1.99
1.995
2
2.005
2.01
x position [m]
0 1 2 3 4 5
−1
−0.5
0
0.5
1
Surge [m/s]
0 1 2 3 4 5
0.5
1
1.5
Deep [m]
0 1 2 3 4 5
−1
−0.5
0
0.5
1
Heave [m/s]
0 1 2 3 4 5
0
2
4
6
time [sec]
Orientation [deg]
0 1 2 3 4 5
−0.4
−0.3
−0.2
−0.1
0
0.1
time [sec]
Angular velocity [rad/s]
Figure 6: Generalized coordinates q and vehicle velocities
ν, in vehicle’s frame for the tracking case (continuous line
for model-free second order sliding mode control, dotted
line for PD control, dashed line for the tracking reference).
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
−500
0
500
Input force on x [N]
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
−500
0
500
Input force on z [N]
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
−40
−20
0
20
40
time [sec]
Input torque [Nm]
Figure 7: Inputs controlled forces u, in vehicle’s frame (con-
tinuous line for model-free second order sliding mode con-
trol, dotted line for PD control).
As for the set-point control case, the position error
and velocities in the constrained direction remain very
small as can be see in figure 6. Also in this figure, the
deep response has a lag from the tracking reference.
As for the input control forces u the steady state re-
semble to those of the set-point control. For the deep
coordinate, the control input tends to to be the same
after some relative small time. Again, the PD does
not provide any force in the constraint direction. The
last can be verified in figure 8 where, for the PD case,
there is no contact force although the position of the
contact point is indeed in contact. For the model-free
2nd order sliding mode control, the contact force has
the same shape as for the set-point control case. The
same transient, due to the numerical consideration for
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
26
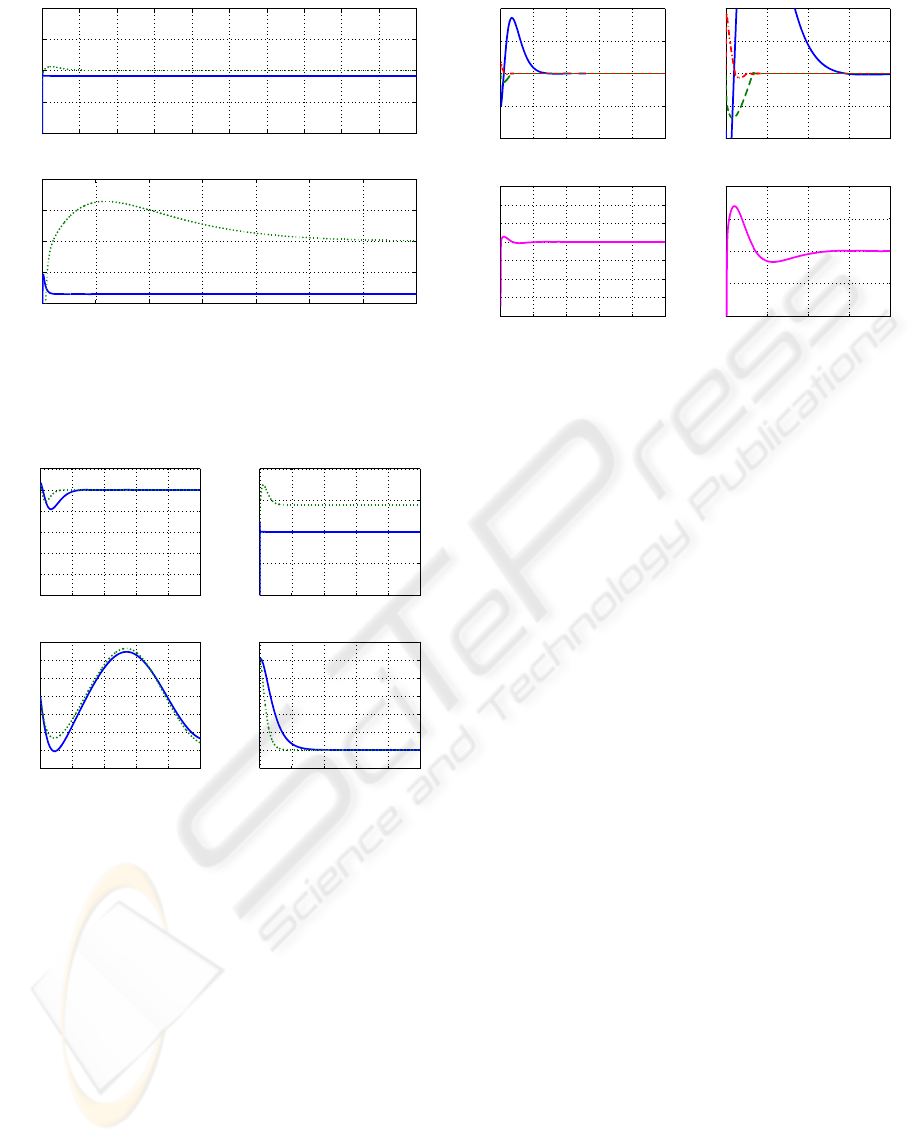
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
−2000
−1000
0
1000
2000
time [sec]
Contac force [N]
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7
−200
−100
0
100
200
time [sec]
Contac force (detail) [N]
Figure 8: Contact force magnitude λ (continuous line for
model-free second order sliding mode control, dotted line
for PD control).
0 1 2 3 4 5
−10
−8
−6
−4
−2
0
2
x 10
−4
x error [m]
0 1 2 3 4 5
−400
−200
0
200
400
Force contact error [N]
0 1 2 3 4 5
−0.2
−0.15
−0.1
−0.05
0
0.05
0.1
0.15
time [sec]
Deep error [m]
0 1 2 3 4 5
−1
0
1
2
3
4
5
6
time [sec]
Orientation error [deg]
Figure 9: Set-point control errors: ˜q = q(t) − q
d
and
˜
λ =
λ(t)− λ
d
(continuous line for model-free second order slid-
ing mode control, dotted line for PD control).
the almost rigid constraint surface, is present. The
tracking errors for the x position and force has been
reduced for the PD case certainly due to numerical
initial conditions. In the tracking of deep, the model-
free 2nd order sliding mode has apparently the same
performance as the simpler PD controller. As it has
been pointed out by other authors, for this kind of sys-
tem, the PD controller remains as the best and simpler
controller for position tracking. However, it does not
track any force reference, which is the essence of the
model-free 2nd order sliding mode control. The last
figure 10 shows the convergence of the extended posi-
tion and force manifolds to zero and induce there after
the sliding mode dynamics.
0 1 2 3 4 5
−0.05
−0.025
0
0.025
0.05
0 0.5 1 1.5 2
−0.01
−0.005
0
0.005
0.01
0 1 2 3 4 5
−0.4
−0.3
−0.2
−0.1
0
0.1
0.2
0.3
0 0.5 1 1.5 2
−0.04
−0.02
0
0.02
0.04
Figure 10: Control variables S
qp
and S
qF
for the model-free
second order sliding mode control.
5 SOME DISCUSSIONS ON
STRUCTURAL PROPERTIES
In the beginning of this study, we were expecting an
involved control structure for submarine robots, in
comparison to fixed-base robots, with additional con-
trol terms to compensate for hydrodynamic and buoy-
ancy forces. However, surprisingly, no additional
terms were required! Due to judicious treatment of
the mathematical model, and careful mapping of ve-
locities through jacobians in vehicle frame and gen-
eralized frame, it suffices only proper mapping of the
gradient of contact forces. This results open the door
to study similar force control structures developed for
fixed-base robots, and so far, the constrained subma-
rine robot control problem seems now at reach.
5.1 Properties of the Dynamics
As it as pointed out in Section 2, the model of a sub-
marine robot can be expressed in either a self space
(where the inertia matrix is constant for some con-
ditions that in practice are not difficult to met) or
in a generalized coordinate space (in which the in-
ertial matrix is no longer constant but the model is
expressed by only one equation, likewise the kine-
matic lagrangian chains). Both representations has
all known properties of lagrangian systems such skew
symmetry for the Coriolis/Inertia matrix, bound-
less of all the components, including buoyancy, and
passivity preserved properties for the hydrodynamic
added effects. The equivalences of these representa-
tion of the same model can be found by means of the
kinematic equation. The last one is a linear opera-
tor that maps generalized coordinates time derivative
ON THE FORCE/POSTURE CONTROL OF A CONSTRAINED SUBMARINE ROBOT
27

with a generalized physical velocity. This relationship
is specially important for the angular velocity of a free
moving object due to the fact that time derivative of
angular representations (such a roll-pitch-yaw) do not
stand for the angular velocity. However, there is al-
ways a correspondence between these vectors. For
external forces this mapping is indeed important. It
relates a physical force/torque wrench to the general-
ized coordinates q = (x
v
,y
v
,z
v
,φ
v
,θ
v
,ψ
v
) whose last
3 components does not represent a unique physical
space. In this work, such mapping is given by J
q
and
appears in the contact force mapping by the normal-
ized operator J
¯
ϕ
. The operator J
q
can be seen as the
difference of a Analytical Jacobian and the Geometric
Jacobian of a robot manipulator.
5.2 The Controller
Notice that the controller exhibits a PD structure
plus a nonlinear I-tame control action, with nonlin-
ear time-varying feedback gains for each orthogonal
subspace. It is in fact a decentralized PID-like, coined
as ”Sliding PD” controller. It is indeed surprising that
similar control structures can be implemented seem-
ingly for a robot in the surface or below water, with
similar stability properties, simultaneous tracking of
contact force and posture. Of course, this is possible
under a proper mapping of jacobians, key to imple-
ment this controller.
5.3 Friction at the Contact Point
When friction at the contact point arises, which is ex-
pected for submarine tasks wherein the contact object
is expected to exhibits a rough surface, with high fric-
tion coefficients, a tangential friction model should
be added in the right hand side. Particular care must
be employed to map the velocities. Complex friction
compensators can be designed, similar to the case of
force control for robot manipulators, therefore details
are omitted.
6 CONCLUSIONS
Although a PD controller, recently validated by
(Smallwood, 2004) has a much simpler structure and
very good performance for underwater vehicles in po-
sition control schemes, it does not deal with the task
of contact force control.
The desired contact force can be calculated via
equation (19) directly in the generalized frame in
which it occurs.
Structural properties of the open-loop dynamics of
submarine robots are key to design passivity-based
controllers. In this paper, an advanced, yet sim-
ple, controller is proposed to achieve simultaneously
tracking of time-varying contact force and posture,
without any knowledge of his dynamic parameters.
This is a significant feature of this controller, since in
particular for submarine robots the dynamics are very
difficult to compute, let alone its parameters.
A simulation study provides additional insight
into the closed-loop dynamic properties for set-point
control and tracking case.
REFERENCES
Fossen, T. I. (1994). Guidance and Control of Ocean Vehi-
cles. Chichester.
IFREMER (1992). Project vortex: Mod
´
elisation et simula-
tion du comportement hidrodynamique d’un v
´
ehicule
sous-marin asservi en position et vitesse. Technical
report, IFREMER.
Liu, Y., Arimoto, S., Parra-Vega, V., and Kitagaki, K.
(1997). Decentralized adaptive control of multiple
manipulators in cooperations. International Journal
of Control, 67(5):649–673.
Olgu
´
ın-D
´
ıaz, E. (1999). Mod
´
elisation et Commande d’un
Syst
`
eme V
´
ehicule/Manipulateur Sous-Marin. PhD
thesis, Laboratoire d’Automatique de Grenoble.
Parra-Vega, V. (2001). Second order sliding mode control
for robot arms with time base generators for finite-
time tracking. Dynamics and Control.
Parra-Vega, V. and Arimoto, S. (1996). A passivity-based
adaptive sliding mode position-force control for robot
manipulators. International Journal of Adaptive Con-
trol and Signal Processing, 10:365–377.
Sagatun, S.I.; Fossen, T. (1991). Lagrangian formulation of
underwater vehicles’ dynamics. Decision Aiding for
Complex Systems, IEEE.
Smallwood, D.A.; Whitcomb, L. (2001). Toward model
based dynamic positioning of underwater robotic ve-
hicles. volume 2. OCEANS,IEEE Conference and Ex-
hibition.
Smallwood, D.A.; Whitcomb, L. (2004). Model-based dy-
namic positioning of underwater robotic vehicles: the-
ory and experiment. IEEE Journal of Oceanic Engi-
neering, 29(1).
Spong M.W., V. M. (1989). Robot Dynamics and Control.
Yoerger, D.; Slotine, J. (1985). Robust trajectory control
of underwater vehicles. Oceanic Engineering, IEEE
Journal, 10(4).
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
28
