AN INCREMENTAL MAPPING METHOD BASED ON A

DEMPSTER-SHAFER FUSION ARCHITECTURE

Melanie Delafosse, Laurent Delahoche, Arnaud Clerentin

RTeAM IUT Dpt Informatique, Amiens, France

Anne-Marie Jolly-Desodt

GEMTEX, Roubaix, France

Keywords: Mobile robot localization, 2D-mapping, uncertainty and imprecision modeling.

Abstract: Firstly this article presents a

multi-level architecture permitting the localization of a mobile platform and

secondly an incremental construction of the environment’s map. The environment will be modeled by an

occupancy grid built with information provided by the stereovision system situated on the platform. The

reliability of these data is introduced to the grid by the propagation of uncertainties managed thanks to the

theory of the Transferable Belief Model.

1 INTRODUCTION

Localization and mapping are fundamental problems

for mobile robot autonomous navigation. Indeed, in

order to achieve its tasks, the robot has to determine

its configuration in its environment. But, if this

result is necessary, it is not sufficient. An estimation

of the uncertainty and the imprecision of this

position should be determined and taken into

account by the robot in order to enable it to act in a

robust way and to adapt its behaviour according to

these two values.

The two notions of uncertainty and imprecision

are distinct ones and they m

ust be clearly defined.

The imprecision results from unavoidable

imperfections of the sensors, (ie) the imprecision

representing the error associated to the measurement

of a value. For example, “the weight of the object is

between 1 and 1.5 kg” is an imprecise proposition.

On the other hand, the uncertainty represents the

belief or the doubt we have on the existence or the

validity of a data. This uncertainty comes from the

reliability of the observation made by the system:

this observation can be uncertain or erroneous. In

other words, the uncertainty denotes the truth of a

proposition. For example, “John is perhaps in the

kitchen” is an uncertain proposition.

In a mobile robotics context, these two notions

are pa

ramount. Using several tools and several

localization algorithms, the mobile robot determines

its configuration. Knowing an estimation of the

uncertainty and the imprecision of this computed

localization, it can adopt an adequate behaviour. For

example, if one of these two values is too high, it

would try to improve the localization estimation by

performing a new localization process.

The key tool used in this purpose is the

Transferab

le Belief Model (TBM) (Smets , 1998), a

non-probabilistic variant of the Dempster-Shafer

theory (Shafer, 1976). Indeed, this theory enables to

easily treat uncertainty since it permits to attribute

mass not only on single hypothesis, but also on the

union of hypotheses. We can thus express ignorance.

So it has enabled us to manage and propagate an

uncertainty from low-level data (sensor data) in

order to get a global uncertainty about the robot

localization. We treat the imprecision independently

from the uncertainty because their non-correlation

have been proved in (Clerentin and all., 2003)

Our dual approach is particularly adapted to the

oblem of data integration in an occupancy grid,

used as part of SLAM paradigm.

We can principally find two types of mapping

para

digm to take into account the notion of distance.

The first paradigm consists of computing a cartesian

representation of the environment which generally

used the Extended Kalman filtering (Leonard and

Durrant-Whyte. , 1992). The second approach based

on occupancy grid maps allows to manage the

438

Delafosse M., Delahoche L., Clerentin A. and Jolly-Desodt A. (2007).

AN INCREMENTAL MAPPING METHOD BASED ON A DEMPSTER-SHAFER FUSION ARCHITECTURE.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 438-445

DOI: 10.5220/0001632504380445

 SciTePress

metric maps, which were originally proposed in

(Elfes,1987.) and which have been successfully

employed in numerous mobile robot systems

(Boreinstein and Koren , 1991). In (Fox and

all,1999)

Dieter Fox introduced a general

probabilistic approach simultaneously to provide

mapping and localization. A major drawback of

occupancy grids is caused by their pure sub-

symbolic nature: they provide no framework for

representing symbolic entities of interest such as

doors, desks, etc (Fox and all,1999).

This paper is divided as follows. In a first part,

we will detail how our grid occupancy is presented

and our uncertain and imprecise sensorial model.

Next we will discuss our localization and mapping

method based on beacon recognizing . Finally we

will present the experimental results.

2 PREAMBLE

2.1 Our Grid Occupancy, Its

Initialisation

We choose to model the environment of our mobile

platform with the occupancy grid tool in 2D. Thus,

the error of sensors measure will be implicitly

managed since we will not manipulate a point (x,y)

but a cell of the grid containing an interval of values

([x],[y]). We choose to center the grid with the

initial position of the platform. Then a cell is defined

by its position in the grid . A cell also contains

information concerning its occupancy degree by

some object of the environment. This latter is

defined by a mass function relative to the

discernment frame

Θ1

= {yes, no}. These two

hypotheses respectively correspond to propositions "

yes, this cell is occupied by an object of the

environment " and " no, this cell is not occupied ".

So the mass function of the cell concerning its

occupation is composed of the three values in [0 ,

1], the mass m

cell

(yes) on the hypothesis {yes},

cell

(no) on the hypothesis {no} and m

cell

(

Θ1

) on the

hypothesis

{yes

∪

no} representing the ignorance on

its occupancy problem. Initially, we have no a-priori

knowledge of the situation. So to model our total

ignorance, all the cells are initialized with the neutral

mass function , that is to say: m

cell

{yes

∪

no} = 1

and m

cell

{yes} = m

cell

{no} = 0.

2.2 Uncertain and Imprecise Sensorial

Model

The platform gets a stereovision system composed

of two omnidirectionnal sensors (see

Figure 1.)

distant of about 50 cm. Every acquisition provides

two pictures of the environment .

The two

omnidirectional

vision sensors

Figure 1: The perception system.

Left sensor Right sensor

Figure 2 : An example of an acquisition.

On Figure 2 all vertical landmarks of the

environment like doors or walls project themselves

to the center and form some sectors of different gray

levels. The positions of these landmarks will permit

to fill the occupancy grid and so to build a map . To

get this information, we should associate each sector

in the first picture with the one that corresponds to it

on the second picture. This stage needs some

treatments on the primary data.

First of all, on each omnidirectional picture, we

define a signal which represents the mean RGB

color from a ring localized around the horizon in the

field of view. In fact, what we want to detect are the

natural vertical beacons of the environment.

Omnidirectional vision system project those vertical

parts of the environment according to radial straight

lines onto the image. During this computation, it is

very important that the rings are centered onto the

projection of the revolution axis of the mirror.

Otherwise, we will not compute the mean RGB

color according to the projection of the vertical

elements of the environment. This centering task is

automatically done with a circular Hough transform

(Ballard,1981). In fact, we look for a circle

corresponding to the projection of the black needle

situated onto the top of the hyperbolic mirror (see

Figure 3) which is situated onto the center of the

mirror.

Then, the two 1D mean RGB signals are

computed from the ring(

Figure 4) and matched

together according to a rule of visibility. In fact, if

an object is detected from one omnidirectional

sensor, it will be visible in a certain area of the other

AN INCREMENTAL MAPPING METHOD BASED ON A DEMPSTER-SHAFER FUSION ARCHITECTURE

439

one, according to the distance between the object

and the mobile robot.

Left sensor

The

black

needle

Right sensor

The

black

needle

Figure 3: Center location computed with a circular Hough

transform.

Left sensor Right sensor

Figure 4: Centered rings to compute the mean RGB

signals.

100°

200°

300°

0°

40°

80°

120°

160°

200°

240°

280°

320°

360°

Left

sensor

Right

sensor

0°

35 cm

60 cm

100 cm

150 cm

300 cm

3000 cm

Figure 5: Correspondences between angles from the left

sensor to the right sensor for ob

jects situated at different

distances from the mobile robot.

mobile

rob

could be close to another one. So, we only keep the

Figure 5 shows the correspondences between the

angle of the left sensor and the angle of the right

sensor according to different distances. We actually

notice that the more the object is close to the

ot, the more the two angles are different.

The detection algorithm is based upon the

derivative of the signal in order to detect sudden

changes of color. When we find such value on the

left sensor, we look for a similar change in the right

sensor signal with a maximum of correlation criteria.

In fact, as you can note on the

Figure 6, a matching

most significant matching according to the

correlation value.

Figure 6 : The two extracted mean color signals from

omnidirectional pictures (to 0 from 140°) of

Figure 4 and

the matching between the left sensor (upper) and the right

sensor (bottom).

We choose to use this indicator (in [0-1]) which

qualify a very good correlation when is near than 1,

to build a degree of uncertainty about the matching

by the way of three masses (see

Figure 7 ).

00,71

absolute correlation coefficent

mass

m(yes)

m(no)

m(yes U no)

Figure 7: Uncertainty about the matching computed with

the correlation coefficient.

When two sectors are matched, we have two

pairs of associated angles on the one hand (angles of

segments that define borders) and on the other hand

a measure of uncertainty on this association. It is

directly linked with a landmark which represents it .

Therefore the pairs define the position of the

landmark and the uncertainty measure its uncertainty

on its existence. So this last value is equal to the set

of three masses coming from the previous fusion in

the discernment frame Θ2= {yes the sectors are

associated; no they do not correspond}

• the mass on the hypothesis “ yes” m

ass

(yes)

• the mass on the hypothesis “ no” m

ass

(no)

the mass on the hypothesis “ I can’t decide about

this matching” m

ass

(yes

∪

no) = m

ass

(

Θ2

) , in other

words this mass represents ignorance.

Then the landmark uncertainty is given by the

following masses in the discernement frame Θ8=

{yes the landmark exist; no it don't exist}:

• the mass on the hypothesis “ yes”

land

(yes) = m

ass

(yes)

• the mass on the hypothesis “ no”

land

(no) = m

ass

(no)

• the mass on the ignorance hypothesis ie “ I can’t

decide about the existence ”

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

440

land

(

Θ8

) =m

ass

(

Θ2

)

Only sectors that have been associated will be

used in the continuation of our survey. The measure

of uncertainty m

land

qualifies the landmark but also

the segment pairs forming borders. Indeed, the

existence of a landmark is linked with the existence

of the borders .

Our data are uncertain but they are also

imprecise because of sensor measurement errors.

This imprecision of measure is managed by the way

of intervals. The second result of this fusion, that is

to say the matching of two angles (

), provides

information about extremities (x

, y

) of the vertical

landmarks in question(

Figure 8) thanks to equations

of triangulation (1) and (2). So we transform our

data in intervals in order to include this imprecision.

We create a error domain empirically around our

measures of angle (

α , β

). Then the operations (1)

and (2) are computed not between reals but on

intervals . We obtain the following equations (3) and

(4):

αβ

tantan

tan

−

(1)

αβ

tantan

−

××

(2)

[]

[] []

αβ

tantan

tan

−

(3)

[]

[] []

αβ

tantan

−

××

(4)

Figure 8 : Sectors matching.

At this level of data exploitation, we have a set

of subpaving characterizing the physical extremities

of each landmark detected, that is to say the object

of which sectors representing it have been matched.

These subpavings form the primitive of our sensorial

model that we will try to link with the beacons

during the time. They are localized by their

coordinates ([xi],[yi]) in the frame relative to the

platform and they have the same measure of

reliability that the landmark ie m

prim

= m

land

. .

3 LOCALISATION AND

MAPPING METHOD

The algorithm consists in matching during the

platform displacement the primitives of the sensorial

model with information known from the

environment that we will call beacons. These

matching once achieved will permit both to correct

the position of beacons and the estimated position of

the platform thanks to the odometry and also to

confirm the existence of beacons. In short we will

exploit data of these beacons to build our occupancy

grid of the surrounding space.

3.1 Definition and Initialisation of

Beacon

A beacon is defined by a set of coordinates in the

reference frame (Xe, Ye) (thus forming a subpaving

of localization ) and by a degree of uncertainty about

its existence composed of three masses as previously

shown. This set of masses is established in the

discernment frame

Θ3

={yes , no}. These two

hypotheses respectively correspond to propositions "

yes, this beacon exists " and " no, this beacon does

not exist". So the function mass concerning its

existence is composed of the three values, the mass

bea

(yes) on the hypothesis {yes}, m

bea

(no) on the

hypothesis {no} and in short m

bea

(

Θ3

) on the

hypothesis

{yes

∪

no} representing the ignorance

about its existence.

A beacon is born from a primitive observed at

instant t that cannot be matched with the existing

beacons at this instant. This new observation is a

landmark not discovered until now or a false alarm.

The only information on the existence of a new

beacon comes from the existence of the primitive

that gave its birth. Then we choose to give the same

measure of uncertainty on the beacon, that is to say

bea t

prim

. Concerning its relative positioning it is

equal to the relative localization subpaving of the

primitive associated. As thereafter we must associate

this beacon to an observation coming from other

acquisitions and should use this one in the updating

of the occupancy grid. So it is more interesting to

manipulate the absolute position . This one is

obtained by the change of a frame in relation to the

configuration of the platform.

Therefore at each instant, new beacons can

appear, and in this case they join the set of the

existing beacons to the following acquisition.

AN INCREMENTAL MAPPING METHOD BASED ON A DEMPSTER-SHAFER FUSION ARCHITECTURE

441

3.2 The Association Method between

Beacons and Primitives

In looking for these matchings, the aim is on the one

hand to get the redundant information permitting to

increase the degree of certainty on the existence of

the beacons and on the other hand to correct their

positioning.

So, at any step, we have several beacons that are

characterized by the center of their subpaving

([x],[y]). Let us call this point the “beacon center”.

The uncertainty of each beacon is represented by the

mass function m

bea t

In this part, we try to propagate the matchings

initialised in the previous paragraph with the

observations made during the robot’s displacement.

In other words, we try to associate beacons with

sensed landmarks.

Suppose we manage q beacons at time n. Each

beacon is characterized by its “beacon center”

(expressed in the reference frame). Let us call this

beacon point (x

, y

). Suppose the robot gets p

observations at time n+1. As we have explained in

the previous paragraph, we are able to compute each

observation localization subpaving ([x

], [y

]) in the

reference frame. So, for each observation, we have

to search among the q beacons the one that

corresponds to it. In other words, we have to match a

beacon center (x

, y

) with an observation subpaving

([x

], [y

]) . The matching criterion we choose is

based on the distance between the beacon center and

the center of observation subpaving ([x

], [y

]).

So at this level, the problem is to match the p

observations obtained at acquisition n+1 with the q

beacons that exist at acquisition n. To reach this aim,

we use the Transferable Belief Model (Smets, 1998)

in the framework of extended open word (Shafer,

1976) because of the introduction of an element

noted * which represents all the hypotheses which

are not modeled, in the frame of discernment.

First we treat the most reliable primitives, that is

to say the “strong” primitives by order of increasing

uncertainty.

For each sensed primitive Pj (j ∈ [1..p]), we

apply the following algorithm:

– The frame of discernment Θ

is composed of:

– the q beacons represented by the hypothesis

Qi (i ∈ [1..q]). Qi means “the primitive Pj is

matched with the beacon Qi”)

– and the element * which means “the primitive

Pj cannot be matched with one of the q

beacons”.

– So: Θ

={Q

, Q

, …, *}

– The matching criterion is the distance between

the center of the subpaving of observation Pj and

one of the beacon centers of Qi

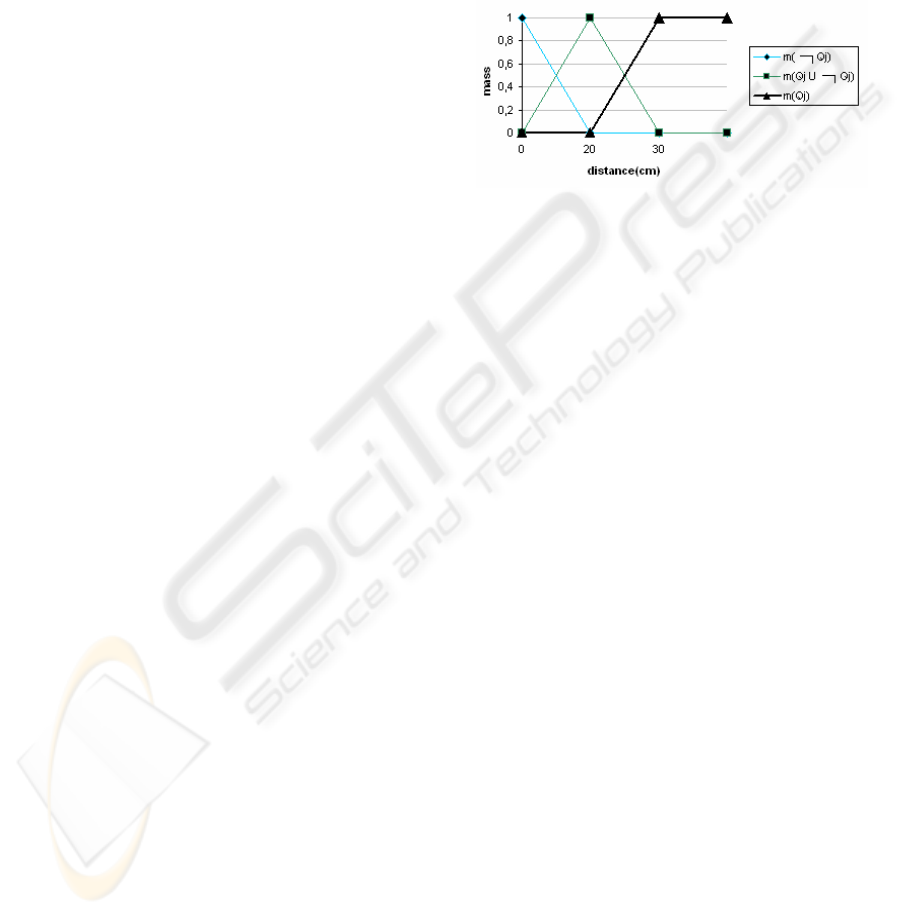
– Considering the basic probability assignment

(BPA) shown

Figure 9, for each beacon Qi we

compute:

– m

(Qi) the mass associated with the

proposition “Pj is matched with Qi”.

– m

(¬Qi) the mass associated with the

proposition “Pj is not matched with Qi”.

– m

(Θ

) the mass representing the ignorance

concerning the observation Pi.

– The BPA is shown on Figure 9.

Figure 9: BPA of the matching criterion.

– After the treatment of all the q beacons, we have

q triplets :

– m

) m

(¬Q

) m

(Θ

)

– m

) m

(¬Q

) m

(Θ

)

– …

– m

) m

(¬Q

) m

(Θ

)

– We fuse these triplets using the disjunctive

conjunctive operator built by Dubois And Prade

(Dubois and Prade, 1998). Indeed, this operator

allows a natural conflict management, ideally

adapted for our problem. In our case, the conflict

comes from the existence of several potential

candidates for the matching, that is to say some near

beacons can correspond to a sensed landmark. With

this operator, the conflict is distributed on the union

of the hypotheses which generate this conflict.

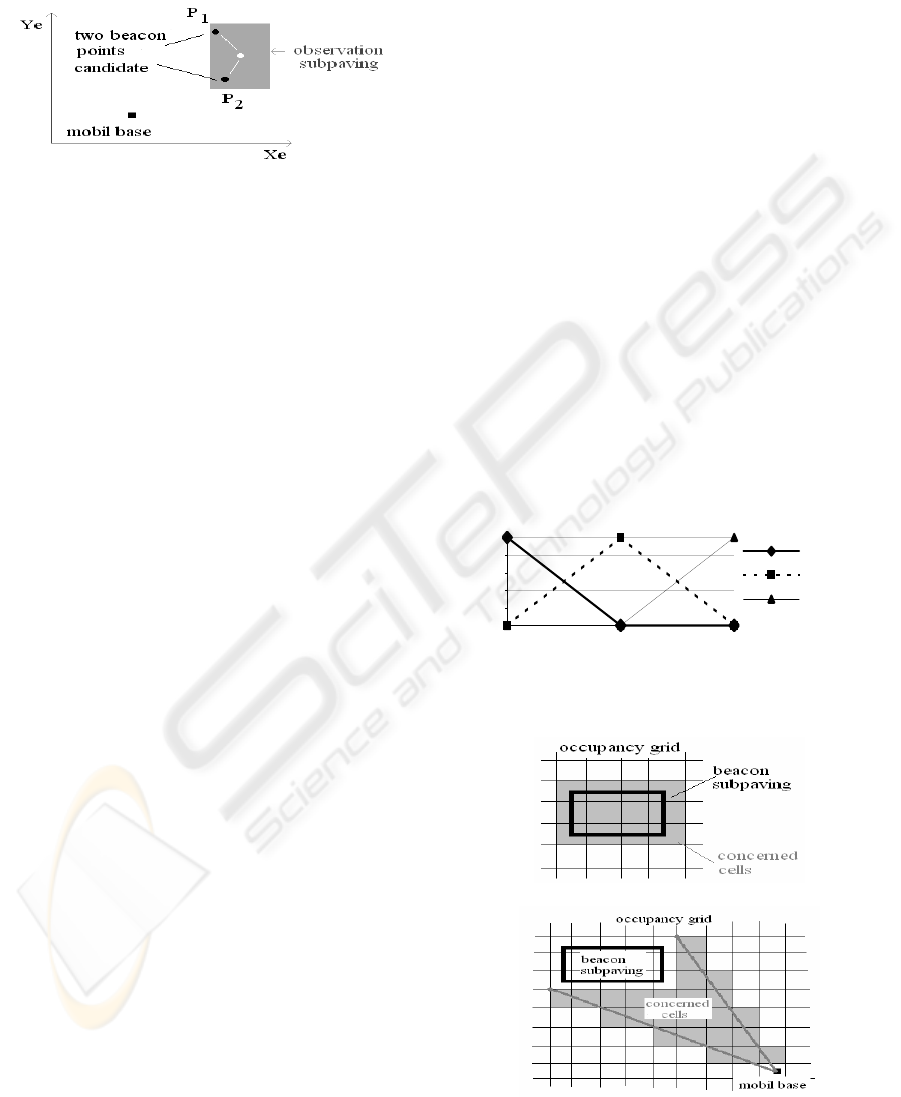
For example, on

Figure 10 , the beacon center P

and P

are candidates for a matching with the

primitive subpaving ([x], [y]). So m

) is high (the

expert concerning P

says that P

can be matched

with ([x], [y])) and m

) is high too. If the fusion is

performed with the classical Smets operator, these

two high values produce some high conflict. But,

with the Dubois and Prade operator, the conflict

generated by the fusion of m

) and m

) is

rejected on m

∪ P

). This means that both P

and P

are candidates for the matching.

– So, after the fusion of the q triplets with this

operator, we get a mass on each single hypothesis

match

(Qi), i ∈ [1..q], on all the unions of hypotheses

match

(Qi ∪ Qj…∪ Qq), on the star hypothesis

match

(*) and on the ignorance m

match

(Θ

– The final decision is the hypothesis which has

the maximal pignistic probability (Smets, 1998). If it

is the * hypothesis, no matching is achieved. This

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

442

situation can correspond to two cases: either the

primitive Pj is an outlier, or Pj can be used to initiate

a new beacon since any existing track can be

associated to it.

Figure 10: An example of two beacons that generate some

conflict.

Once a matching is achieved, the uncertainty of

the concerned beacon has to be updated. This

uncertainty is denoted by the mass function m

bea

defined on the frame of discernment Θ

. This

updating has to take the reliability of the matched

primitive (mass function m

prim

) and also the

uncertainty of the matching into account. This

matching uncertainty is deduced from the pignistic

probability of the selected matched primitive by the

mass function m2 shown on

Figure 11. For example,

if the pignistic probability is equal to 0.75, the

matching uncertainty is denoted by the following

mass function m

: m

(yes)=m

({yes, no})=0.5 ;

(no)=0.

Finally, the beacon uncertainty at time t (denoted

by the mass function m

bea t

) is updated by fusing the

beacon uncertainty at the previous time t-1, the

primitive uncertainty (m

prim

) and the matching

uncertainty (m

): m

bea t

= m

bea t-1

∩ m

prim

∩ m

where ∩ is the fusion operator of Smets.

Let us recall that this mass function is composed

of three values: m

bea t

(yes), m

bea t

(no), m

bea t

(Θ

3.3 The Management of non Associated

Beacons

Concerning the beacons that have not been matched

at this instant, our first reflection was the following.

As no observation can be associated, it implies that

our beacon has not been detected to this acquisition.

Therefore the first idea was to put in doubt its

existence in decreasing its degree of existence. But

even if the beacon is no more visible from instant t

for example because the mobile platform is moving ,

the object nevertheless exists. It is necessary not to

lose this information at the level of the map. Then

we decide not to modify the degree of existence of a

beacon which was not matched.

3.4 The Consequences on our Grid

A new beacon or a beacon that have been associated

to an observation provide two kinds of information

both on the occupied space and on the empty space

of our grid. Let us examine the case of one of these

beacons at time t to explain this phenomenon. As we

have already said, this beacon has a measure of

uncertainty on its existence. It is defined by the mass

function m

bea t

3.4.1. The Occupied Space

The existence of a beacon is directly bound to the

occupation of cells containing its localization

subpaving. Therefore the degree of occupation of

these cells must take the degree of existence of the

beacon into account. It is achieved thanks to the

fusion with the operator of Smets of these two mass

functions. So if the mass function of the beacon

indicates rather a certain existence then this fusion

will increase the degree of occupation of concerned

cells. On the contrary, if it indicates an existence

which is somewhat unreliable, the fusion will

reverberate this doubt on these same cells. A cell is

concerned by the fusion if its intersection with the

localization subpaving is not empty, they appear in

gray on

Figure 12a.

0.2

0.4

0.6

0.8

00.51

maximal pignistic probabililty

mass

m( NO)

m({YES,NO})

m(YES)

Figure 11: Mass function m2 of the matching uncertainty.

Figure 12: a) Occupied Space, b) Free Space.

AN INCREMENTAL MAPPING METHOD BASED ON A DEMPSTER-SHAFER FUSION ARCHITECTURE

443

The fusion is the following:

cell t

= m

cell t-1

∩ m

bea t

3.4.2 The Free Space

On the other hand, since this beacon has been

associated to an observation, it implies that the space

between the point of observation in this case the

mobile platform and the beacon does not contain any

obstacle. This space is therefore free. But it is free in

relation with the existence of the beacon.

This operation is achieved in the same way as

previously, that is to say merging with the operator

of Smets. But this time, we fuse its current

occupation degree with a mass function m

built as

being the “contrary” of the mass function m

bea t

Because the more the beacon is denoted by a high

mass on the hypothesis {yes, I exist} , the more the

mass on the hypothesis {no, this cell is not

occupied} for the cell of the free space (

Figure 12 b)

must increase . This function m

is the next one:

{ no} = m

bea t

{yes}, m

{ yes ∪ no} = m

bea t

{

yes ∪ no} and m

{yes} = m

bea t

{ no}.

And this fusion is given by the following

expression : m

cell t

= m

cell t-1

∩ m

To resume we get a set of beacons and a

occupancy grid of obstacles of the surrounding

space.

3.5 The Correction Method

Now we use these data to correct the position of

beacons at first and then the estimated position of

the mobile platform . These stages are under

development. We currently use the correction

modules presented below that will be to improve in

future works. The beacons are characterized by an

error domain of center (x,y). We notice that this

center, disposed on the grid, is surrounded with the

cells of different occupation levels. To take account

of the information we modify the position of the

beacon. In fact, we choose the center of gravity of a

window 5 x 5 cells around the center pondered by

their respective mass m

cell

(yes) , as the point that

now characterizes the position of the beacon.

Let us remember that the configuration of the

mobile platform is estimated with odometric

information. Or we know the classical phenomena of

cumulative error if no correction method is achieved

(Delafosse and all , 2005). Our correction module is

based on the cumulative error minimization. We

limit the real possible positions of the platform to

centers of cells of a window 3 x 3 around the

position estimated by odometry. The kept position

among the nine will be the p position that minimizes

the accumulated sum of distances between beacons

and primitives observed since the p position.

4 EXPERIMENTAL RESULTS

We present experimental results obtained in a

structured indoor environment on

Figure 13 . The

platform is stopped to every stereoscopic acquisition

achieved every 30 cms. The managed trajectory is a

large boucle represented in yellow on the

Figure 14.

The natural landmarks mainly observed are the

framings of doors, corners , walls and pillars .In

Figure 14 we present the obtained map building. The

blue cells correspond to the empty space and the red

one to the occupied space. The intermediate colors

highlight the merging of the occupied and free state.

We can notice that the method is robust since most

observable landmarks are integrated to the map

according to the real map presented in grey on the

graphs. We can easily detect for example the corners

of the “cross” hall and the free space between each

others. We can also notice the certainty of the free

space is clearly represented by the color purple. Our

approach complementary to the probabilistic one,

form an alternative to the SLAM paradigm based on

the occupancy grid. We can observe the correlation

between the uncertainty of a landmark position

estimation and the updating cell values.

5 CONCLUSION

In this article we have presented an architecture of

fusion and integration of data for the SLAM

paradigm. It is based on a representation of

occupancy grid type. The originality of the

proposition is on the one hand the propagation of

uncertainties on several levels of treatments and on

the other hand the management uncoupled of

imprecision and uncertainty. The association of

these two concepts permits an important reliability

in the process of new primitive integrations in the

map. This step is crucial since it conditions the

global consistency of the cartographic representation

on an important number of acquisitions. Moreover

our approach permits to solve the problem of

“primitive number explosion” which generally

implies a divergence of the SLAM process. Besides

the precision obtained on the position estimation of

observable landmarks is relatively important. So the

«symbolic» approach presented constitutes an

interesting alternative to methods classically used in

this domain that are generally probabilistic.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

444

Figure 13: The experimental environment (scale 1m x

1m). We focus on the part of the corridor which represente

a cross.

Figure 14 : The resulting map.

REFERENCES

Ballard D. H., "Generalizing the Hough transform to

detect arbitrary shapes."

Pattern Recognition, v. 13, n.

2, pp. 111-122, 1981.

Boreinstein J. , Koren Y., 1991. “Histogrammic in-motion

mapping for mobile robot obstacle avoidance”, IEEE

Trans. On rob. and auto., Vol. 7, N°4, pp. 1688-1693

Clerentin A., Delahoche L., Brassart E., Drocourt C.,

2003. "Uncertainty and error treatment in a dynamic

localization system", proc. of the 11th Int. Conf. on

Advanced Robotics (ICAR03), pp.1314-1319,

Coimbra, Portugal.

Delafosse M., Clerentin C., Delahoche L., Brassart E.,

2005. “Uncertainty and Imprecision Modeling for the

Mobile Robot Localization Problem” – IEEE

international conference on robotics and automation

ICRA 05 , Barcelona, Spain.

Dubois D., Prade H., Sandri S., 1998. Possibilistic logic

with fuzzy constants and fuzzily restricted quantifiers.

In: Logic Programming and Soft Computing,

(Martin,T.P. et Arcelli-Fontana,F., Eds.), Research

Studies Press, Baldock, England, 69-90.

Elfes A. 1987. “Sonar-based real world mapping and

navigation”, IEEE Journal of robotics and automation,

Vol. RA-3, N°3, pp. 249-265, June 1987

Fox D., Burgard W. , Thrun S. ,1999. "Probabilistic

Methods for Mobile Robot Mapping", Proc. of the

IJCAI-99 Workshop on Adaptive Spatial

Representations of Dynamic Environments.

Leonard J.J., Durrant-Whyte H.F. , 1992. “Dynamic map

building for an autonomous mobile robot”, The

International Journal of Robotics Research, Vol. 11

n°4, August

Royère C, 2002. “Contribution à la résolution du conflit

dans le cadre de la théorie de l’évidence”, thèse de

doctorat de l’Université de Technologie de

Compiègne.

Shafer GA, 1976. A mathematical theory of evidence,

Princeton : university press.

Smets Ph ,1998. “The Transferable Belief Model for

Quantified Belief Representation.”, Handbook of

Defeasible Reasoning and Uncertainty Management

Systems, Kluwer Ed, pp 267-301.

AN INCREMENTAL MAPPING METHOD BASED ON A DEMPSTER-SHAFER FUSION ARCHITECTURE

445