INTEGRATED DESIGN OF A MECHATRONIC SYSTEM

The Pressure Control in Common Rails

Paolo Lino and Bruno Maione

Dipartimento di Elettrotecnica ed Elettronica, Politecnico di Bari, via Re David 200, 70125, Bari, Italy

Keywords:

Mechatronic systems, Virtual prototyping, AMESim

, Modelling, Automotive control.

Abstract:

This paper describes the integrated design of the pressure control in a common-rail injection system. Mechan-

ical elements and the embedded controller are considered as a whole, using a multi-disciplinary approach to

modelling and simulation. The virtual prototype, which provides the detailed geometrical/physical model of

the mechanical parts, plays the role of a surrogate of a reference hardware prototype in reduced-order mod-

elling, validation, and/or in tuning the control parameters. The results obtained by the proposed approach are

compared and validated by experiments.

1 INTRODUCTION

The innovative characters of mechatronic systems

lie with a special design process thinking about the

mechanical parts and the embedded controllers as a

whole. On the contrary, the traditional design of de-

vices combining mechanical and electronic elements

considers components belonging to different physi-

cal domain separately. Moreover controllers are con-

ceived for already existing plants. Hence the physi-

cal properties and the dynamical behaviour of parts,

in which energy conversion plays a central role, are

not determined by the choices of the control engi-

neers and therefore are of little concern to them. Their

primary interests, indeed, are signal processing and

information management, computer power require-

ments, choice of sensors and sensor locations, and so

on. So it can happen that poorly designed mechan-

ical parts do never lead to good performance, even

in presence of advanced controllers. On the other

hand, a poor knowledge of how controllers can di-

rectly inﬂuence and balance for defects or weaknesses

in mechanical components does not help in achieving

quality and good performance of the whole process.

Aiming at an integrated design, in mechatronic sys-

tems the interactions among mechanical, electronic

and information processing elements are considered

in all the design steps, beginning with the early stages

(Stobart et al., 1999),(van Amerongen and Breedveld,

2003).

If the design choices must be made before assem-

bling interacting parts of a physical prototype and if

these parts belong to different physical domains (such

as mechanics, electronics, hydraulics and control) the

virtual prototyping approaches, which are surrogates

for preliminary physical realizations, face many difﬁ-

culties. The ﬁrst one is due to the fact that each phys-

ical domain has speciﬁc modelling and simulation

tools. Unfortunately, indeed, there is a gap between

tools for evaluating the designed components in dif-

ferent domains. For example, mechanical engineers

usually refer to ﬁnite element approaches/packages as

an important tool for dimensioning mechanical parts

and for evaluating their dynamical properties. Only

after a complex order-reduction process (modal anal-

ysis) the so obtained models are reduced in a form

suitable for the control analysis and design. On the

other hand, control modelling tools are based on oper-

ators (transfer functions, frequency response) and/or

on state equations descriptions, which, in many cases,

do not have a straightforward connection with the crit-

ical parameters of physical design. However, it is

clear that an appropriate modelling and simulation ap-

proach can not be ﬁtted into the limitations of one for-

malism at time, particularly in the early stages of the

design process. Hence, it is necessary a combination

Lino P. and Maione B. (2007).

INTEGRATED DESIGN OF A MECHATRONIC SYSTEM - The Pressure Control in Common Rails.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 11-18

DOI: 10.5220/0001632800110018

 SciTePress

of different methodologies in a multi-formalism ap-

proach to modelling supported by an appropriate sim-

ulation environment.

In mechatronic applications, the Bond Graphs in-

troduced by (Paynter, 1960) provide a continuous sys-

tem modelling approach, oriented to a class of inter-

connected and completely different systems and tar-

geted to many user groups. Bond Graphs are very use-

ful in analysing and designing components built from

different energetic media and can represent dynamical

systems at higher level of abstraction than differen-

tial equations (van Amerongen and Breedveld, 2003),

(Ferretti et al., 2004).

In this paper, we referred to AMESim

(Ad-

vanced Modelling Environment for performing Sim-

ulations of engineering systems) (IMAGINE S.A.,

2004) a Bond Graph-based, multi-domain mod-

elling/optimization tool for the virtual prototyping

of the physical/geometrical characteristics of a Com-

pressed Natural Gas (CNG) injection system. In a ﬁrst

step, we used this tool to obtain a virtual prototype, as

similar as possible to the actual ﬁnal hardware. Then,

with reference to this prototype, we also determined

a reduced order model in form of transfer function

and/or state space model, more suitable for analytical

(or empirical) tuning of the pressure controller of the

CNG injection systems. Using the virtual prototype

in these early design stages enabled the evaluation of

the inﬂuence of the geometrical/physical alternatives

on the reduced model used for the controller tuning.

Then, based on this reduced model, the controller set-

tings were designed and adjusted in accordance with

the early stages of the mechanical design process. Fi-

nally, the detailed physical/geometric model of the

mechanical parts, created by the AMESim package,

was exported ad used as a module in a simulation

program, which enabled the evaluation of the con-

troller performance in the closed-loop system. In

other words, the detailed simulation model surrogated

for a real hardware.

2 THE INTEGRATED DESIGN

APPROACH

In this paper, we consider the opportunity of integrat-

ing different models, at different level of details, and

different design tools, to optimize the design of the

mechanical and control systems as a whole. To sum

up, the integrated design can take advantage of pecu-

liarities of different speciﬁc software packages. The

effectiveness of the approach is illustrated by means

of a case study, the pressure control of a CNG injec-

tion system for internal combustion engines, which

represents a benchmark for the evaluation of perfor-

mances of the approach. Experimental results give a

feedback of beneﬁts of the integration of the mechan-

ical and control subsystems design.

The integrated design involves the development

of a virtual prototype of the considered system using

an advanced modelling tool (AMESim in this paper),

which is employed for the analysis of the system per-

formances during the different developing steps. Ac-

tually, the virtual prototype could be assumed as a re-

liable model of the real system. Further, a low order

analytical model of the real system can be developed

to simplify the controller design. Since AMESim can

represent physical phenomena at different level of de-

tails, it is exploited to verify assumptions in build-

ing the analytical model. Then, the control system

is designed using a speciﬁc software package, i.e.

MATLAB/Simulink

, and tested on the virtual pro-

totype. The virtual prototype allows to perform safer,

less expensive, and more reliable tests than using the

real system.

3 APPLICATION EXAMPLE

We consider a system composed of the following el-

ements (Fig. 1): a fuel tank, storing high pressure

gas, a mechanical pressure reducer, a solenoid valve

and the fuel metering system, consisting of a com-

mon rail and four electro-injectors. Two different con-

ﬁgurations were compared for implementation, with

different arrangements of the solenoid valve affecting

system performances (i.e. cascade connection, ﬁgure

1(a), and parallel connection, Fig.1(b), respectively).

Detailed AMESim models were developed for each

of them, providing critical information for the ﬁnal

choice. Few details illustrate the injection operation

for both layouts.

With reference to Fig. 1(a), the pressure reducer

receives fuel from the tank at a pressure in the range

between 200 and 20 bars and reduces it to a value of

about 10 bar. Then the solenoid valve suitably reg-

ulates the gas ﬂow towards the common rail to con-

trol pressure level and to damp oscillations due to in-

jections. Finally, the electronically controlled injec-

tors send the gas to the intake manifold for obtain-

ing the proper fuel air mixture. The injection ﬂow

only depends on rail pressure and injection timings,

which are precisely driven by the Electronic Control

Unit (ECU). The variable inﬂow section of the pres-

sure reducer is varied by the axial displacement of a

spherical shutter coupled with a moving piston. Pis-

ton and shutter dynamics are affected by the applied

forces: gas pressure in a main chamber acts on the

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

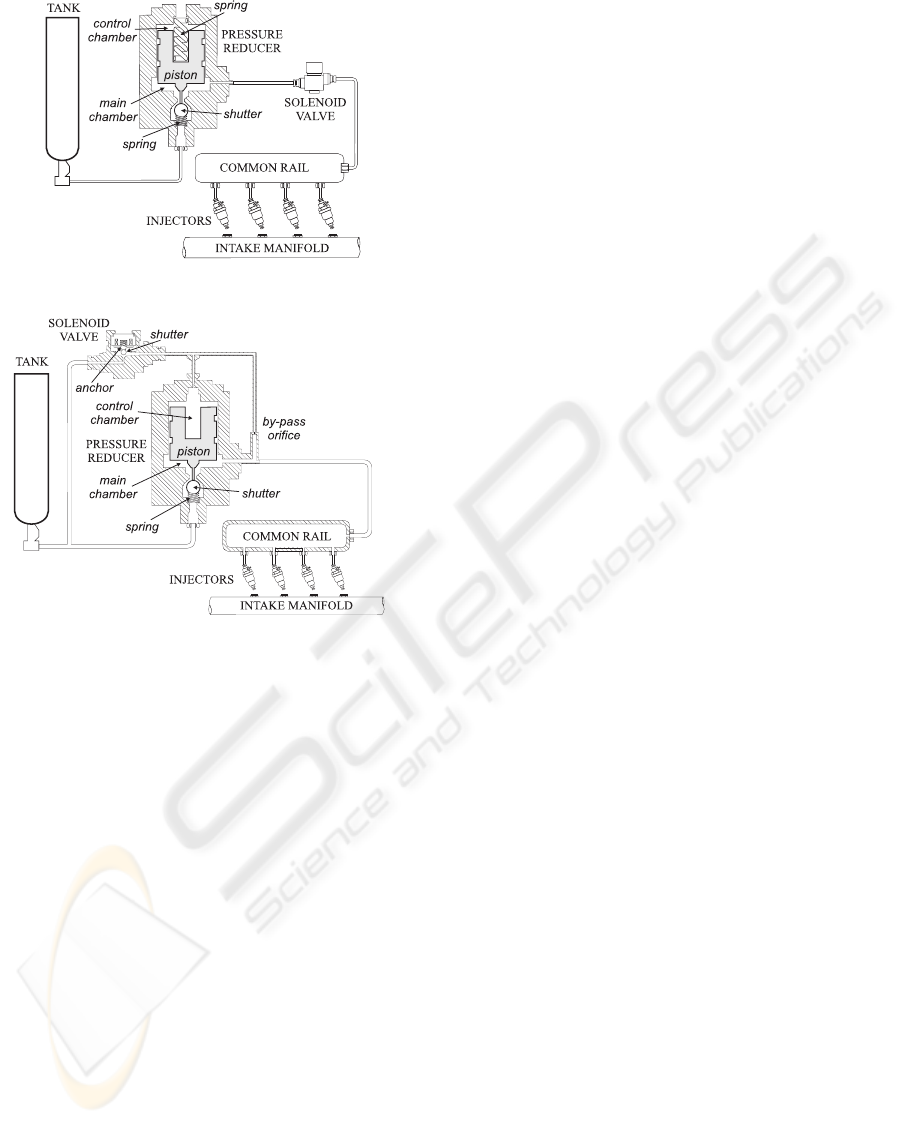
(a)

(b)

Figure 1: Block schemes of the common rail CNG injec-

tion systems; (a) cascade connection of solenoid valve; (b)

parallel connection of solenoid valve.

piston lower surface pushing it at the top, and elastic

force of a preloaded spring holden in a control cham-

ber pushes it down and causes the shutter to open. The

spring preload value sets the desired equilibrium re-

ducer pressure: if the pressure exceeds the reference

value the shutter closes and the gas inﬂow reduces,

preventing a further pressure rise; on the contrary, if

the pressure decreases, the piston moves down and

the shutter opens, letting more fuel to enter and caus-

ing the pressure to go up in the reducer chamber (see

(Maione et al., 2004) for details).

As for the second conﬁguration (Fig. 1(b)), the

fuel from the pressure reducer directly ﬂows towards

the rail, and the solenoid valve regulates the in-

take ﬂow in a secondary circuit including the con-

trol chamber. The role of the force applied by the

preloaded spring of control chamber is now played by

the pressure force in the secondary circuit, which can

be controlled by suitably driving the solenoid valve.

When the solenoid valve is energized, the fuel en-

ters the control chamber, causing the pressure on the

upper surface of the piston to build up. As a con-

sequence, the piston is pushed down with the shut-

ter, letting more fuel to enter in the main chamber,

where the pressure increases. On the contrary, when

the solenoid valve is non-energized, the pressure on

the upper side of the piston decreases, making the pis-

ton to raise and the main chamber shutter to close un-

der the action of a preloaded spring (see (Lino et al.,

2006) for details).

On the basis of a deep analysis performed on

AMESim virtual prototypes the second conﬁguration

was chosen as a ﬁnal solution, because it has advan-

tages in terms of performances and efﬁciency. To

sum up, it guarantees faster transients as the fuel can

reach the common rail at a higher pressure. Moreover,

leakages involving the pressure reducer due to the al-

lowance between cylinder and piston are reduced by

the lesser pressure gradient between the lower and up-

per piston surfaces. Finally, allowing intermediate po-

sitions of the shutter in the pressure reducer permits

a more accurate control of the intake ﬂow from the

tank and a remarkable reduction of the pressure oscil-

lations due to control operations. A detailed descrip-

tion of the AMESim model of the system according

the ﬁnal layout is presented in section 4 (Fig. 2).

4 AMESIM MODEL OF THE CNG

INJECTION SYSTEM

AMESim is a virtual prototyping software produced

by IMAGINE S.A., which is oriented to lumped pa-

rameter modelling of physical elements, intercon-

nected by ports enlightening the energy exchanges be-

tween pairs of elements and between an element and

its environment. AMESim enables the modelling of

components from different physical domains and the

integration of these different elements in an overall

system framework. It also guarantees a ﬂexible archi-

tecture, capable of including new components deﬁned

by the users.

By assumption, the pressures distribution within

the control chamber, the common rail and the injec-

tors is uniform, and the elastic deformations of solid

parts due to pressure changes are negligible. The

pipes are considered as incompressible ducts with

friction and a non uniform pressure distribution. Tem-

perature variations are taken into account, affecting

the pressure dynamics in each subcomponent. Be-

sides, only heat exchanges through pipes are con-

sidered, by properly computing a thermal exchange

coefﬁcient. The tank pressure plays the role of a

maintenance input, and it is modelled by a constant

INTEGRATED DESIGN OF A MECHATRONIC SYSTEM - The Pressure Control in Common Rails

Figure 2: AMESim model of the CNG injection system.

pneumatic pressure source. To simplify the AMESim

model construction some supercomponents have been

suitably created, collecting elements within a single

one.

4.1 Pressure Reducer and Common

Rail

The main components for modelling the pressure re-

ducer are the Mass block with stiction and coulomb

friction and end stops, which computes the piston

and the shutter dynamics through the Newton’s sec-

ond law of motion, a Pneumatic ball poppet with con-

ical seat, two Pneumatic piston, and an Elastic con-

tact modelling the contact between the piston and the

shutter. The Pneumatic piston components compute

the pressure forces acting upon the upper and lower

piston surfaces. The viscous friction and leakage due

to contact between piston and cylinder are taken into

account through the Pneumatic leakage and viscous

friction component, by specifying the length of con-

tact, the piston diameter and the clearance. Finally, a

Variable volume with pneumatic chamber is used to

compute the pressure dynamics as a function of tem-

perature T and intake and outtake ﬂows ˙m

, ˙m

out

, as

well as of volume changes due to mechanical part mo-

tions, according to the following equation:

˙p =



˙m

− ˙m

out

+ ρ



, (1)

where p is the fuel pressure, ρ the fuel density and

V the taken up volume. The same component is used

to model the common rail by neglecting the volume

changes.

Both pressure and viscous stresses contribute to

drag forces acting on a body immersed in a moving

ﬂuid. In particular, the total drag acting on a body

is the sum of two components: the pressure or form

drag, due to pressure gradient, and the skin friction

or viscous drag, i.e. Drag force = Form drag + Skin

friction drag. By introducing a drag coefﬁcient C

depending on Reynolds number, the drag can be ex-

pressed in terms of the relative speed v (Streeter et al.,

1998):

Drag = C

ρAv

/2. (2)

Moving shutters connecting two different control vol-

umes are subject to both form drag and skin fric-

tion drag. The former one is properly computed by

AMESim algorithms for a variety of shutters, con-

sidering different poppet and seat shapes. As for the

latter, it is computed as a linear function of the ﬂuid

speed by the factor of proportionality. It can be ob-

tained by noting that for a spherical body it holds

Form Drag = 2πDµv (Streeter et al., 1998), being µ

the absolute viscosity and D the shutter diameter. The

moving anchor in the solenoid valve experiences a

viscous drag depending on the body shape. In par-

ticular, the drag coefﬁcient of a disk is C

= 1.2, and

the skin friction drag can be computed using eq. 2.

Since, by hypothesis, the anchor moves within a ﬂuid

with uniform pressure distribution, the form drag is

neglected.

4.2 Pipes

The continuity and momentum equations are used to

compute pressures and ﬂows through pipes so as to

take into account wave propagation effects. In case

of long pipes with friction, a system of nonlinear par-

tial differential equations is obtained, which is imple-

mented in the Distributive wave equation submodel

of pneumatic pipe component from the pneumatic li-

brary. This is the case of pipes connecting pressure re-

ducer and common rail. The continuity and momen-

tum equations can be expressed as follows (Streeter

et al., 1998):

∂ρ

∂t

+ ρ

∂v

∂x

= 0, (3)

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

∂u

∂t

u|u| = 0, (4)

where α is the sound speed in the gas, d is the pipe

diameter, f is the D’Arcy friction coefﬁcient depend-

ing on the Reynolds number. AMESim numerically

solves the above equations by discretization.

For short pipes, the Compressibility + friction

submodel of pneumatic pipe from is used, allowing to

compute the ﬂow according the following equation:

q =

2D∆p

Lρf

, (5)

where ∆p is the pressure drop along the pipe of length

L. The pipes connecting common rail and injectors

are modelled in such a way.

Heat transfer exchanges are accounted for by the

above mentioned AMESim components, provided

that a heat transfer coefﬁcient is properly speciﬁed.

For a cylindrical pipe of length L consisting of a ho-

mogeneous material with constant thermal conductiv-

ity k and having an inner and outer convective ﬂuid

ﬂow, the thermal ﬂow Q is given by (Zucrow and

Hoffman, 1976):

Q =

2πkL∆T

, (6)

where ∆T is the temperature gradient between the in-

ternal and external surfaces, and r

and r

are the ex-

ternal and internal radiuses, respectively. With ref-

erence to the outside surface of the pipe, the heat-

transfer coefﬁcient U is:

. (7)

4.3 Solenoid Valve and Magnetic

Circuits

The AMESim model for the solenoid valve is com-

posed of the following elements: a solenoid with

preloaded spring, two moving masses with end stops

subject to viscous friction and representing the mag-

net anchor and the shutter respectively, and a compo-

nent representing the elastic contact between the an-

chor and the shutter. The intake section depends on

the axial displacement of the shutter over the conical

seat and is computed within the Pneumatic ball pop-

pet with conical seat component, which also evaluates

the drags acting on the shutter. The solenoid valve

is driven by a peak-hold modulated voltage. The re-

sulting current consists of a peak phase followed by

a variable duration hold phase. The valve opening

time is regulated by varying the ratio between the hold

phase duration and signal period, namely the control

signal duty cycle. This signal is reconstructed by us-

ing a Data from ASCII ﬁle signal source that drives a

Pulse Width Modulation component.

To compute the magnetic force applied to the

anchor, a supercomponent (Solenoid with preloaded

spring in Fig. 2) modelling the magnetic circuit has

been suitably built, as described in the following. The

magnetic ﬂux within the whole magnetic circuit is

given by the Faraday law:

ϕ = (e

− R

)/n, (8)

where ϕ is the magnetic ﬂux, R the n turns winding

resistance, e

the applied voltage and i

the circuit

current. Flux leakage and eddy-currents have been

neglected. The magnetomotive-force MMF able to

produce the magnetic ﬂux has to compensate the mag-

netic tension drop along the magnetic and the air gap

paths. Even though most of the circuit reluctance is

applied to the air gap, nonlinear properties of the mag-

net, due to saturation and hysteresis, sensibly affect

the system behaviour. The following equation holds:

MMF = MMF

+ MMF

= H

+ H

, (9)

where H is the magnetic ﬁeld strength and l is the

magnetic path length, within the magnet and the gap

respectively. The air gap length depends on the actual

position of the anchor. The magnetic induction within

the magnet is a nonlinear function of H. It is assumed

that the magnetic ﬂux cross section is constant along

the circuit, yielding:

B = ϕ/A

= f (H

) = µ

, (10)

where A

is the air gap cross section and µ

is the

magnetic permeability of air. The B− H curve is the

hysteresis curve of the magnetic material. Arranging

the previous equations yields to ϕ, B and H. The re-

sulting magnetic force and circuit current are:

= A

/µ

, (11)

= MMF/n. (12)

The force computed by the previous equation is ap-

plied to the mass component representing the anchor,

so that the force balance can be properly handled by

AMESim.

4.4 Injectors

The injectors are solenoid valves driven by the ECU

in dependence of engine speed and load. The whole

injection cycle takes place in a 720

interval with a

delay between each injection of 180

. A supercompo-

nent including the same elements as for the solenoid

valve has been built to model the electro-injectors.

The command signal generation is demanded to the

ECU component, which provides a square signal driv-

ing each injector and depending on the current engine

speed, injector timings and pulse phase angle.

INTEGRATED DESIGN OF A MECHATRONIC SYSTEM - The Pressure Control in Common Rails

5 CONTROLLER DESIGN

In designing an effective control strategy for the in-

jection pressure it is necessary to satisfy physical

and technical constraints. In this framework, model

predictive control (MPC) techniques are a valuable

choice, as they have shown good robustness in pres-

ence of large parametric variations and model uncer-

tainties in industrial processes applications. They pre-

dict the output from a process model and then impress

a control action able to drive the system to a reference

trajectory (Rossiter, 2003). A 2

order state space

analytical model of the plant (Lino et al., 2006) is

used to derive a predictive control law for the injection

pressure regulation. The model trades off between ac-

curacy in representing the dynamical behaviour of the

most signiﬁcant variables and the need of reducing

the computational effort and complexity of controller

structure and development. The design steps are sum-

marized in the following. Firstly, the model is lin-

earized at different equilibrium points, in dependence

of the working conditions set by the driver power re-

quest, speed and load. From the linearized models it

is possible to derive a discrete transfer function repre-

sentation by using a backward difference method. Fi-

nally, a discrete Generalised Predictive Contrl (GPC)

law suitable for the implementation in the ECU is de-

rived from the discrete linear models equations.

By considering the duty cycle of the signal driving

the solenoid valve and the rail pressure as the input

u and output y respectively, a family of ARX mod-

els can be obtained, according the above mentioned

design steps (Lino et al., 2006):



1− a

−1



y(t) =



−1

− b

−2



u(t), (13)

where q

−1

is the shift operator and a

, b

are con-

stant parameters. The j-step optimal predictor of a

system described by eq. 13 is (Rossiter, 2003):

ˆy(t + j|t) = G

∆u(t + j− 1) +F

y(t), (14)

where G

and F

are polynomials in q

−1

, and ∆ is

the discrete derivative operator. Let r be the vec-

tor of elements y(t + j), j = 1,... ,N, depending on

known values at time t. Then eq. (14) can be ex-

pressed in the matrix form

y = G

u + r, being

u =

[∆u(t), .. .,∆u(t + N − 1)]

, and G a lower triangular

N × N matrix (Rossiter, 2003).

If the vector w is the sequence of future reference-

values, a cost function taking into account the future

errors can be introduced:

J = E

u+ r− w)

u+ r− w) + λ

(15)

where λ is a sequence of weights on future control

actions. The minimization of J with respect of

u gives

the optimal control law for the prediction horizon N:

u =



G+ λI



−1

(w− r). (16)

At each step, the ﬁrst computed control action is ap-

plied and then the optimization process is repeated af-

ter updating all vectors. It can be shown (Lino et al.,

2006) that the resulting control law for the case study

becomes:

∆u(t) = k

w(t) +



+ k

−1



y(t) + k

∆u(t − 1),

(17)

where [k

] depends on N.

6 SIMULATION AND

EXPERIMENTAL RESULTS

To assess the effectiveness of the AMESim model in

predicting the system behaviour, a comparison of sim-

ulation and experimental results has been performed.

Since, for safety reasons, air is used as test ﬂuid, the

experimental setup includes a compressor, providing

air at a constant input pressure and substituting the

fuel tank. The injection system is equipped with four

injectors sending the air to a discharging manifold.

Moreover, a PC system with a National Instrument

acquisition board is used to generate the engine speed

and load signals, and a programmable MF3 develop-

ment master box takes the role of ECU driving the

injectors and the control valve.

Figure 3 refers to a typical transient operating con-

dition, and compares experimental and simulation re-

sults. With a constant 40 bar input pressure, the sys-

tem behaviour for a constant t

= 3ms injectors open-

ing time interval, while varying engine speed and

solenoid valve driving signal has been evaluated. The

engine speed is composed of ramp proﬁles (Fig. 3(c)),

while the duty cycle changes abruptly within the inter-

val [2%,12%] (Fig. 3(d)). Figures 3(a) and 3(b) show

that the resulting dynamics is in accordance with the

expected behaviour. A maximum error of 10% con-

ﬁrms the model validity.

After the validation process, the AMESim vir-

tual prototype was used to evaluate the GPC con-

troller performances in simulation by employing the

AMESim-Simulink interface, which enabled us to ex-

port AMESim models within the Simulink environ-

ment. The interaction between the two environments

operates in a Normal mode or a Co-simulation mode.

As for the former, a compiled S-function containing

the AMESim model is generated and included in the

Simulink block scheme, and then integrated by the

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

0 20 40 60 80 100 120 140 160

Time [s]

Control Chamber Pressure [bar]

experimental pressure

simulated pressure

(a)

0 20 40 60 80 100 120 140 160

Time [s]

Rail Pressure [bar]

experimental pressure

simulated pressure

(b)

0 20 40 60 80 100 120 140 160

Time [s]

Engine Speed [rpm x 1000]

(c)

0 20 40 60 80 100 120 140 160

Time [s]

duty cycle [%]

(d)

Figure 3: AMESim simulation and experimental results when varying duty cycle. and engine speed, with a constant t

= 3ms;

(a) control chamber pressure; (b) common rail pressure; (c) engine speed; (d) control signal duty cycle.

Figure 4: AMESim-MATLAB co-simulation interface.

Simulink solver. As for the latter, which is the case

considered in this paper, AMESim and Simulink co-

operate by integrating the relevant portions of models,

as shown in ﬁgure 4.

The GPC controller was tuned referring to models

linearized at the starting equilibrium point, according

to design steps of Section 5. The test considered ramp

variations of the engine speed and load, for the system

controlled by a GPC with a N = 5 (0.5s) prediction

horizon. The input air pressure from the compres-

sor was always 30bar. The rail pressure reference was

read from a static map depending on the working con-

dition and had a sort of ramp proﬁle as well. The ﬁnal

design step consisted in the application of the GPC

control law to the real system.

In Fig. 5, the engine speed accelerates

from 1100rpm to 1800rpm and then decelerates to

1100rpm, within a 20s time interval (Fig. 5(b)).

The control action applied to the real system guar-

antees a good reference tracking, provided that its

slope does not exceed a certain value (Fig. 5(a), time

intervals [0, 14] and [22, 40]). Starting from time

14s, the request of a quick pressure reduction causes

the control action to close the valve completely (Fig.

5(c)) by imposing a duty cycle equal to 0. Thanks to

injections, the rail pressure (Fig. 5(a)) decreases to

the ﬁnal 5bar reference value, with a time constant

depending on the system geometry; the maximum er-

ror amplitude cannot be reduced due to the actuation

variable saturation. Fig. 5(d) shows the injectors’ ex-

citing time during the experiment. It is worth to note

that simulation and experimental results are in good

accordance, supporting the proposed approach.

7 CONCLUSIONS

In this paper, we presented a procedure for integrat-

ing different models and tools for a reliable design,

optimization and analysis of a mechatronic system as

a whole, encompassing the real process and the con-

trol system. The effectiveness of the methodology has

been illustrated by introducing a practical case study

involving the CNG injection system for internal com-

INTEGRATED DESIGN OF A MECHATRONIC SYSTEM - The Pressure Control in Common Rails

0 5 10 15 20 25 30 35 40

Time [s]

Rail Pressure [bar]

experimental pressure

pressure reference

simulated pressure

(a)

0 5 10 15 20 25 30 35 40

1.2

1.4

1.6

1.8

Time [s]

Engine Speed [rpm x 1000]

(b)

0 5 10 15 20 25 30 35 40

Time [s]

duty cycle [%]

experimental duty cycle

simulated duty cycle

(c)

0 5 10 15 20 25 30 35 40

Time [s]

Injection Timing [ms]

(d)

Figure 5: AMESim model and real system responses for speed and load ramp variations and a 30bar input pressure, when

controlled by a GPC with N = 5; (a) common rail pressure; (b) engine speed (c) duty cycle; (d) injectors exciting time interval.

bustion engines. The design process was organized

in few steps: analysis of different candidate conﬁgu-

rations carried out with the help of virtual prototypes

developed in the AMESim environment; design and

performance evaluation of controllers designed on a

simpler model of the plant employing the virtual pro-

totypes; validation of the control law on the real sys-

tem. The implementation of the control law on the

real system represented a benchmark for the evalua-

tion of performances of the approach. Experimental

results gave a feedback of beneﬁts of the integration

of the mechanical and control subsystems design, and

proved the validity of the methodology.

REFERENCES

Ferretti, G., Magnani, G., and Rocco, P. (2004). Virtual

Prototyping of Mechatronic Systems. Annual Reviews

in Control, (28):193206.

Lino, P., Maione, B., Amorese, C., and DeMatthaeis, S.

(2006). Modeling and Predictive Control of a New In-

jection System for Compressed Natural Gas Engines.

In IEEE CCA 2006 International Conference, Mu-

nich, Germany.

Maione, B., Lino, P., DeMatthaeis, S., Amorese, C., Man-

odoro, D., and Ricco, R. (2004). Modeling and Con-

trol of a Compressed Natural Gas Injection System.

WSEAS Transactions on Systems, 3(5):2164–2169.

Paynter, H. (1960). Analysis and Design of Engineering

Systems. M.I.T. Press, Cambridge, MA.

Rossiter, J. (2003). Model-Based Predictive Control: a

Practical Approach. CRC Press, New York.

Stobart, R., A.May, Challen, B., and Morel, T. (1999). New

Tools for Engine Control System Development. An-

nual Reviews in Control, (23):109–116.

Streeter, V., Wylie, K., and Bedford, E. (1998). Fluid Me-

chanics. McGraw-Hill, New York, 9th edition.

IMAGINE S.A. (2004). AMESim User Manual v4.2.

Roanne, France.

van Amerongen, J. and Breedveld, P. (2003). Modelling

of Physical Systems for the Design and Control of

Mechatronic Systems. Annual Reviews in Control,

(27):87–117.

Zucrow, M. and Hoffman, J. (1976). Gas Dynamics. John

Wiley & Sons, New York.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics