ELECTRO HYDRAULIC PRE-ACTUATOR MODELLING OF AN

HYDRAULIC JACK

Salazar Garcia Mahuampy, Viot Philippe

Laboratoire Matériaux Endommagement Fiabilité et Ingénierie des Procédés (LAMEFIP), France

Nouillant Michel

Keywords: Three-stage servo-valve, modeling, hydraulic jack.

Abstract: Before the realization of testing devices such as a high speed (5m/s) hydraulic hexapod with a high load

capacity (60 tons and 6 tons for static and dynamic operating mode), the simulation is an essential step.

Hence from softwares such as SimMecanics, we have performed an electro hydraulic model of the servo-

valve-jack part by using parameters and recorded results with mono axis testing bench of high-speed

hydraulic jack (5m/s), which has a high loading capacity (10 tons for static and 1 ton for dynamic operating

mode). The high-speed jack is provided by two parallel three-stage servo-valves. Each three-stage servo-

valve supplies 600L/mm. Therefore the unit allows us to obtain a realistic model of an extrapolated hexapod

from the mono axis currently used. The aim of this article is to provide a modeling of the second and third

stage servo valves by comparison of the typical experimental reading and the computed curves obtained

from simulation.

1 INTRODUCTION

The main difficulties of the modeling of an actuator

hydraulic hexapod are servo valve models. In the

case of electrical actuators operating in control

voltage, the torque is got from the control voltage

and the rotation speed of the motor. In the case of

hydraulic actuator, for a current control of servo

valve given, the efforts provided by the jack depend

on the flow rate and consequently they depend also

on the speed of the jack and leakages. This aspect is

not taken into account by using the classical

frequency model of the servo valve (Faisandier,

1999), (Mare, 2002), (Thayer, 1965).

At first, we will present the hydraulic model of

the servo valve + jack system. In a second time, a

nonlinear modeling will be developed. Lastly, the

results obtained from the modeling will be presented

and analyzed.

2 ELECTRO HYDRAULIC

SYSTEM

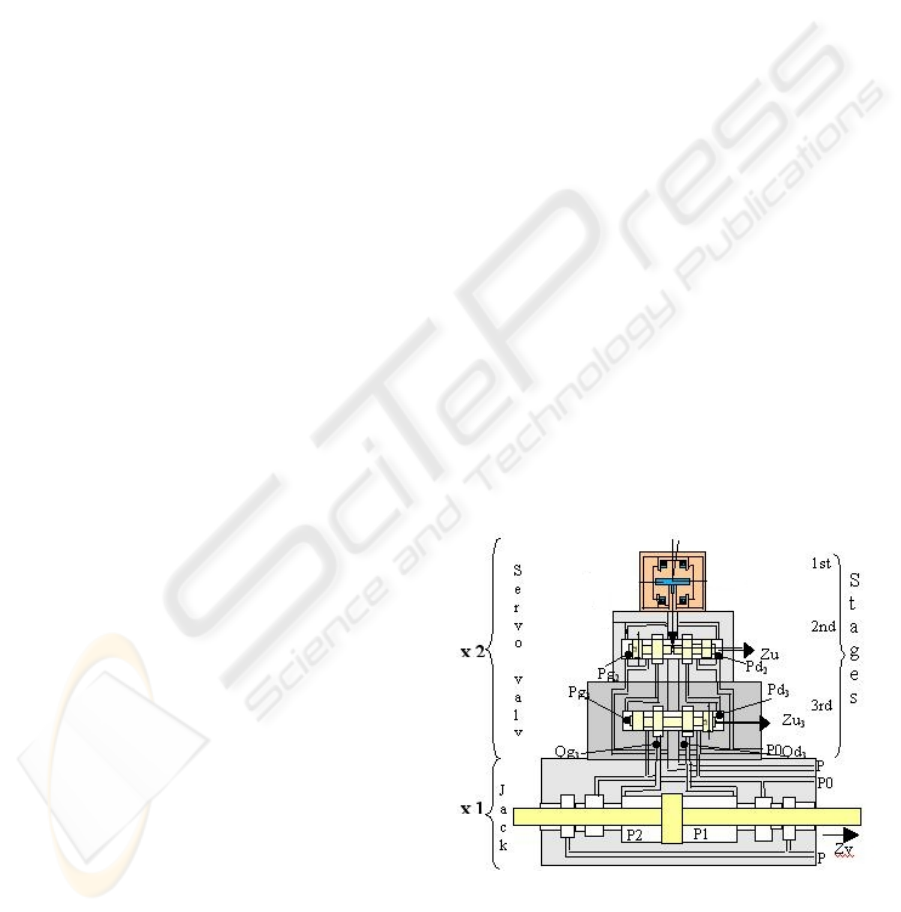
Figure 1: Diagrammatic section of system.

Figure 1 shows a model with three-stage servo valve

and a jack. The symbol "x2" and "x1" indicate

respectively the presence in the system of two

Garcia Mahuampy S., Philippe V. and Michel N. (2007).

ELECTRO HYDRAULIC PRE-ACTUATOR MODELLING OF AN HYDRAULIC JACK.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 59-64

DOI: 10.5220/0001632900590064

 SciTePress

parallel servo valves supplying the jack. A servo

valve is controlled by an electrical stage (1

stage),

followed by a 2nd stage and a 3rd hydraulic

amplification stage (Faisandier,1999), (Guillon,

1961).

A control current applied to the system input is

named i. The double potentiometric hydraulic

divisor of the first stage, leads to two pressures Pg

and Pd

applied to the end of the slide on the 2nd

stage, the flow rates provided by this 2nd stage are

named Qg

and Qd

, applied to the control of the

slide displacement of the 3rd stage of the servo

valve.

The third stage generates the flow rates Qg

and

taking part in the sum of the flows entering and

going out of the jack chambers, and leading, through

instantaneous volumes of the chambers, and the

compressibility coefficient of the oil, to the pressure

variation in each chamber. The servo valve is

supplied with pressure P

and reservoir return line P.

3 MODELING

3.1 Servo Valve Linear Model

Figure 2 shows linear diagram of a servo valve

modeling (Pommier,2000).

Figure 2: Linear diagram of the servo valve.

Km: Gain between the current and the torque.

ωn: Undamped natural frequency of the pallet inertia of

the 1st stage.

ξ : Damping ratio of the friction of the pallet.

kf: Gain displacement in torque of the nozzle pallet unit.

: Gain in flow rate of hydraulic amplification.

: Surface of the slide ends of the 2nd stage.

: Gain of the feedback torque.

K’

: Gain in flow rate of the 2nd stage slide.

: Effective volume when the slide is centered.

: Surface of the slide ends of the 3rd stage.

: Slide mass of the 3rd stage.

K’

: Gain in flow rate of the 3rd stage.

One notes that for this model, the K’

and K’

coefficients characterize the flow rate as a function

of the slide positions. For the second stage, the K’

coefficient gives a good approximation within a

large part of the operating area, contrary to the K’3

coefficient suggesting that the speed of the jack does

not depend on the load.

3.2 Hydraulic Nonlinear Model

Figure 3 shows the general diagram describing the

non-linear model of servo-valve-jack system.

Figure 3: Nonlinear model of the servo valve + jack.

One takes into account the hydrodynamic forces

applied to the various slides of the servo valves.

These forces take part in the nonlinear behavior of

the device. This functional diagram shows that the

behavior of the servo valve and the jack cannot be

dissociated and must be treated as such.

We have developed a nonlinear model of the

servo-valve-jack unit allowing to determine, for a

given control current, the effort supplied by the jack

from the pressure variations within the control

volumes formed by the jack chambers. This pressure

variation after temporal integration defines the

pressure within the right and left chambers of the

jack. The difference of these pressures multiplied by

the active section of the piston gives the effort

supplied by the jack.

In our case, the main difficulty is the nonlinear

modeling of the servo valve; more particularly we

have to take into account a finite number of sensitive

parameters and the hydraulic nonlinear behavior

laws. In addition to the nonlinearities resulting from

the hydraulic potentiometer, the pressure flow will

be taken into account from the following relation:

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

.|P|K=Q Δ (1)

We assume that the flow rate of the fluid is

viscous and incompressible, as turbulent type.

The transient flow rate associated with fluid

incompressibility is proportional to the rate of

change of pressure in a volume of control and may

be expressed as:

se QQdtdVdtdPV −=+ )/()/)(/(

(2)

Where β is the bulk modulus of the fluid.

We also take into account the hydrodynamic

forces on the various slides of the servo-valves,

leading to the nonlinear behavior of the device.

(

)

gQF

(3)

Where γ is the specific gravity (kg/m3) and g is

the gravitational acceleration.

The angular displacement of the frame engine

versus the current is given by:

)(

...

222

θθθϕθ

signFLKrJLZuKrPliKm ss +++=−Δ+

(4)

With ∆P2=Pg2-Pd2 difference of pressure

between the two slide ends of the 2nd stage.From

the equation (2) one can obtain the evolution laws of

the pressures Pg2 and Pd2.

⎟

⎠

⎞

⎜

⎝

⎛

−−+−

222021

2202

ZuSPgPKfQQg

ZuSVdt

dPg

⎟

⎠

⎞

⎜

⎝

⎛

+−+−

−

222021

2202

ZuSPdPKfQQd

ZuSVdt

dPd

(5)

(6)

Where, S

is the flow rate caused by the

motion of the slide and Qg

and Qd

are the flow

rates resulted from the pressure applied to the

section of fixed openings S1, Qb is the flow rate

from the nozzle tip.

By applying the fundamental principle of

dynamics we obtain the sum of the forces applied to

the slide of the 2nd stage:

)(

222222

θψθ

signFZuKrZuZumFLKrPS shd +++=−−Δ

(7)

Where S2ΔP2 is the difference of forces applied

to the ends of the slide, Kr2Lθ is the force due to the

stiffness and the deformation of the pallet.

The flow rate Qd2 and Qg2 provided by the 2nd

stage is given by the equation (1). The equation of

Qd2, Qg2 taking into account the slide covering and

the resulting leakage. The modeling of the slide

covering is exponential modeling, where ε is a

constant. The very low value of ε ensures the

continuity in the opening model of the slide and the

leakage resulted from the slide covering.

From the equation (2), and (7), one can obtain

the evolution laws of the pressures and the sum of

the forces related to the third stage and the jack

hydraulic.

4 IMPLEMENTATION AND

RESULTS

At first, we have identified the parameters of the

nonlinear model from the high-speed 5m/s servo-

valve-jack unit of LAMEFIP laboratory. This first

step gives us some experimental reference

parameters for the validity of our servo-valve model.

The servo valve composed of the first and second

stages and the second servo valve composed of the

third stage are respectively hydaustar 550 and 1160

type servo valve. All the parameter values of the

model estimated or measured of the electro

hydraulic system for the second and third stages are

summarized in table 1.

Table 1: Parameter values of the second and third stages.

Parameters

Manufact

urer data

Estimated

data

Length magnetic

pallet

31.2e-3

(m)

-----------

Outdistance

between magnetic

axis pallets and

metering jets

10.5e-3

(m)

------------

Dbuse

Diameter of nozzle

tip

0.18e-3

(m)

----------

Sbuse

Surface of nozzle

tip

2.54e-8

)

Length between

magnetic axis

pallets and metering

jets

----------

55e-6

(m)

Kbuse Gain of nozzle tip ----------

0.039

/s/m)

Gain of flow rate of

the fixed section

----------

1.5e-9

/s/m)

Gain of leakage in

the stage

----------

5.15e-12

/s/m)

Volume control

when the slide is

centered

19.5e-9

)

-----------

Surface of slide

3.38e-5

)

-----------

J Pallet inertia ----------

4e-7

(Kg m

)

ELECTRO HYDRAULIC PRE-ACTUATOR MODELLING OF AN HYDRAULIC JACK

Viscous friction

coefficient in

rotation of the pallet

----------

9e-4

(Nm/rd s)

Stiffness of the slide

of the stage

2100

(N/m)

------------

Slide masse 9e-3 (Kg) ------------

Viscous friction

coefficient in slide

-------- 6 (Ns/m)

Gain of leakage in

the stage

-----------

1e-12

/s/m)

Ε Lap ----------- 3.7e-6 (m)

Gain of flow rate of

volume control in

the stage

-----------

6e-4

/s/m)

Surface of slide

5e-4 (m

)

------------

Volume control

when the slide is

centered

8.6e-6 (m

)

------------

Slide masse

276e-3

(Kg)

------------

Viscous friction

coefficient in slide

-----------

1000

(Ns/m)

After completing the estimated parameters, we

compare the typical experimental datas supplied by

the manufacturer such as the flow rate – current

characteristics for the second stage, the frequency

response of the second and third stages with the

curves resulting from the model using both the

estimated values and the measured values.

4.1 Flow Rate – Current

Characteristics

We have compared the flow rate Qd2 of the second

stage of the servo valve under differential pressure

of 70 bar when the current i varies in the range [

-I

max

; +I

max

], I

max

is the maximum value of the

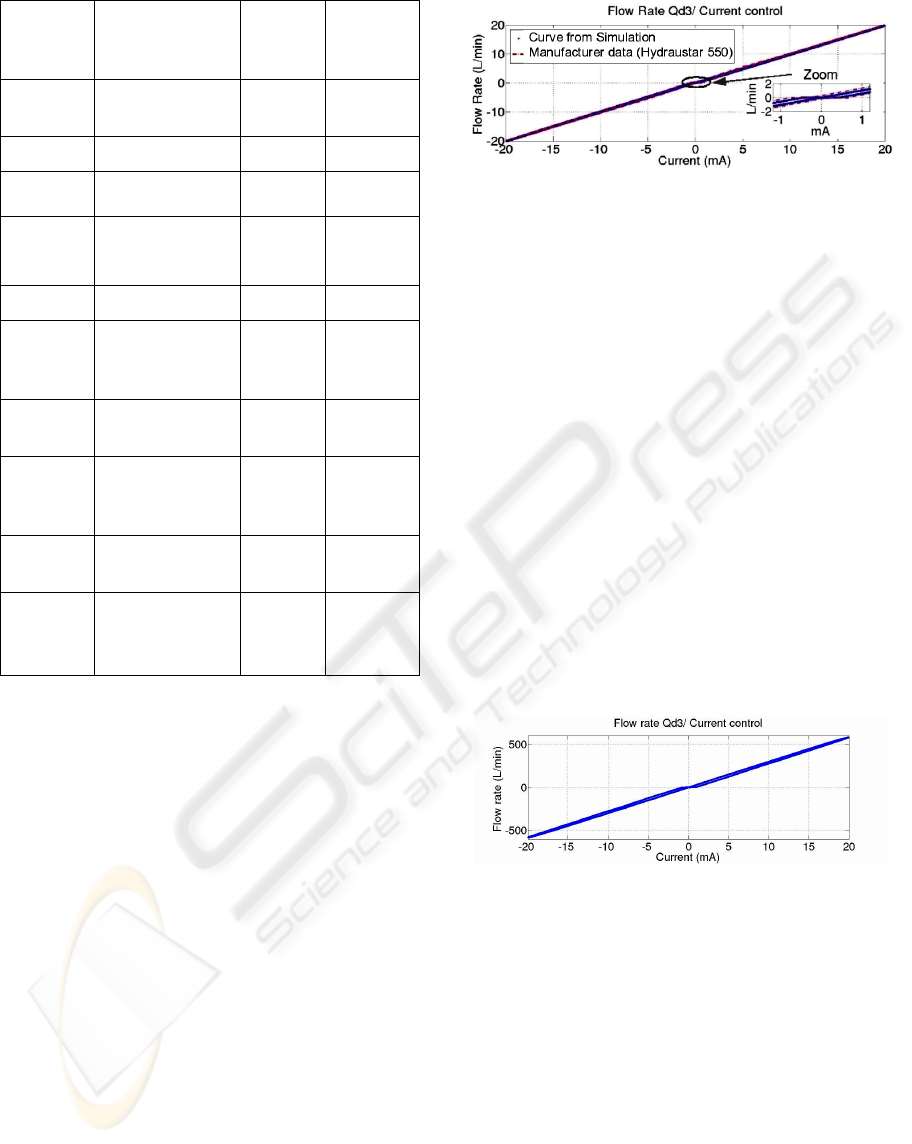
current modulus. The figure 4 shows the flow rate

Qd2 – current i characteristics for the 550

Hydraustar servo valve (second stage) supplied by

the manufacturer and those obtained from the model.

Figure 4: Flow rates / control currents characteristics

supplied by manufacturer and those obtained from the

model.

As shown in the figure 4, we can observe that the

result obtained from the model and that provided by

the manufacturer are similar when the current input

reaches the maximal value of 20 mA. The maximal

flow rate value provided by the driver servo valve

reaches 20 l/min. One can observe the role of the

leakages when the slide position is near the

hydraulic zero as shown in the inset of the figure4.

These leakages result from the taking into account of

the laps and the clearances between the slide and the

sleeve. The figure 5 shows the computed flow rate

Qd3 of the third stage of the servo valve under

differential pressure of 70 bar when the courant

varies from –I

max

and + I

max

. We obtain in this

particular configuration, a maximal computed value

of the flow rate provided by the servo valve of +/-

600 l/min. This value matches the manufacturer data

for this servo valve model.

Figure 5: Flow rate Qd3/ control current characteristics

obtained by simulation.

4.2 Frequency Response

We have compared the characteristic curves

obtained from the bench test measurement (by using

a servo valve flow with normalized decreasing of the

pressure of 70 bar for different input levels) with

the curves computed from our model.

4.2.1 First and Second Stage

The figure 6 shows the comparison of the

manufacturer curves with those obtained from the

model for the similar operating conditions: provided

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

pressure Ps = 210 bar, differential pressure 70 bar,

100% nominal current.

Figure 6: Frequency response for 100% of the nominal

current. (for -3 dB, 110 Hz < f < 130 Hz, -90°, 230 Hz < f

< 250 Hz, theoretical curve).

The frequency response corresponding to 100 % of

nominal current obtained from the model gives a

cut-off frequency of 115 Hz for a gain of –3 dB and

a frequency of 180 Hz for a phase lag of 90°. The

cut-off frequency for –3 dB obtained with the model

is in the limit range of the dispersion of frequencies

provided by the manufacturer. For phase lag of 90°,

the frequency error between both curves is estimated

from 20% to 28 %.

Figure 7: Frequency response for 25 % of the nominal

current. (for –3 dB, 210 Hz < f < 230 Hz and for -90°, 250

Hz < f < 280 Hz, theoretical curve).

The figure 7 shows the frequency comparison of

the manufacturer curves and those obtained with the

model for the similar operating conditions: Provided

pressure Ps = 210 bar, pressure difference 70 bar,

25 % of the nominal current.

The frequency response for 25% of the nominal

current obtained from the model gives us a cut-off

frequency of 220 Hz for a gain of -3 dB and a

frequency of 210 Hz for a phase lag of 90°. The cut-

off frequency corresponding to a gain of -3 dB is in

the limit range of the dispersion of the manufacturer

frequencies. The frequencies related to the phase lag

of 90° obtained by modeling and those provided by

manufacturer are different. The error is estimated

from 16 % to 25 %. The computed curve shapes for

the second stage are different from those supplied by

the manufacturer. This difference should depend

directly on the estimated values of the pallet inertia

and its friction coefficient. An infinitesimal variation

of these values leads to the under damping observed

in amplitude plot of the bode diagram.

4.2.2 Third Stage

We compare the frequency responses of the serial

servo valve 1160, corresponding to the third stage,

with the coupling of the serial servo valve 550

related to the driving stage. The figure 8 shows the

typical response supplied by the manufacturer for

100 % of the nominal input signal.

Figure 8: Frequency response for 100 % of the nominal

current.

The driving servo valve is provided with a

pressure Ps of 210 bar. The cut-off frequencies in

the limit ranges of the dispersion for a frequency

response corresponding to 100 % of the nominal

ELECTRO HYDRAULIC PRE-ACTUATOR MODELLING OF AN HYDRAULIC JACK

current match respectively 70 Hz and 85 Hz for –3

dB and phase lag 90° for flow rates Qd3 and Qg3 of

600 l/min.

The frequency response for 100 % of the

nominal value of the current obtained from the

model gives a cut-off frequency of 70 Hz

corresponding to a gain of –3 dB and a frequency of

73 Hz for a phase lag of 90°. One observes that the

results obtained for the servo valves corresponding

to the second and third stages from the model and

those supplied by the manufacturer are close.

Nevertheless, one can note that a difference between

the curves amplitude from the manufacturer and

those obtained from the model. Indeed, the

manufacturer curves show an under damping

probably caused by the implementation of the

corrector in the system whereas we have performed

the modeling without corrections in loop control.

5 CONCLUSION

In our work, one can note that the servo valve is the

limiting element of the servo valve + jack system.

The flow rate values (20 l/min and 600 l/min

provided by the second and the third stage

respectively), like the bandwidth values of the

driving servo valve corresponding to the second

stage and those of the amplification stage e.g. the

third stage, obtained from the model and supplied by

manufacturer are rather similar. These results

suggest that the estimated values, which cannot be

measured, such as the gap xo between the nozzle and

the pallet, the inertia J and the viscous friction

coefficients of the pallet Φ, the friction coefficients

of the slides Ψ

and the flow rate gains Kbuse, K1,

, K2, Kf

, are fairly close to the physical values of

the type 550 and 1160 Hydraustar servo valve. We

have shown that the nonlinear model presented in

this work have allowed us the accurate simulation of

the nonlinear behavior of three stage servo valves

between the current input and the flow rate output.

This model allows the taking into account of the

pressure into the jack chambers as a function of the

forced stress. Hence with this model is possible to

computed the dynamic and static behavior, the latter

corresponds to the short circuit generated by jack

stoppers.

At this stage, the interfacing with the

SimMecanics software, by introducing as input this

corresponding to the effort between two ”bodies”,

the quantity (P1-P2)Sp (Sp: useful piston surface),

will provide as output from the software, the speed

and the relative position of both bodies.

ACKNOWLEDGEMENTS

Special thanks go to Mr. Terrade (Hydraustar

company) for supplying technical support.

REFERENCES

Faisandier, J., 1999. Mécanismes hydrauliques et

pneumatiques , 8

édition, Paris, Dunod.

Mare, J.C., 2002, Actionneurs Hydrauliques, Commande .

Techniques de l’ingénieurs, traité l’informatique

industrielle.S731.

Thayer, W.J., 1965, Transfer functions for moog servo

valves , Technical bulletin I03, MOOG INC. Springer-

Verlag.

Guillon, M., 1961, Etude et détermination des systèmes

hydrauliques, Paris, Dunod.

Pommier, V., Lanusse P., Oustaloup A., 2000, Commande

CRONE d'un actionneur hydraulique. In Journée

Franco-Tunisiennes, Monastir, Tunisie.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics