FUZZY LOGIC ALGORITHM FOR MOBILE ROBOT CONTROL

Viorel Stoian and Cristina Pana

University of Craiova, Mechatronics Department, Decebal Street No. 107, Craiova, Romania

Keywords: Fuzzy logic algorithm, mobile robots, obstacole avoidance, trajectory controller.

Abstract: This paper presents a fuzzy control algorithm for mobile robots which are moving next to the obstacle

boundaries, avoiding the collisions with them. Four motion cycles (programs) depending on the proximity

levels and followed by the mobile robot on the trajectory (P1, P2, P3, and P4) are shown. The directions of

the movements corresponding to every cycle, for every reached proximity level are presented. The sequence

of the programs depending on the reached proximity levels is indicated. The motion control algorithm is

presented by a flowchart showing the evolution of the functional cycles (programs). The fuzzy rules for

evolution (transition) of the programs and for the motion on X-axis and Y-axis respectively are described.

Finally, some simulations are presented.

1 INTRODUCTION

Fuzzy set theory, originally developed by Lotfi

Zadeh in the 1960’s, has become a popular tool for

control applications in recent years (Zadeh, 1965).

Fuzzy control has been used extensively in

applications such as servomotor and process control.

One of its main benefits is that it can incorporate a

human being’s expert knowledge about how to

control a system, without that a person need to have

a mathematical description of the problem.

Many robots in the literature have used fuzzy

logic (Song, 1992, Khatib, 1986, Yan, Ryan, Power,

1989 …). Computer simulations by Ishikawa feature

a mobile robot that navigates using a planned path

and fuzzy logic. Fuzzy logic is used to keep the

robot on the path, except when the danger of

collision arises. In this case, a fuzzy controller for

obstacle avoidance takes over.

Konolige, et al. use fuzzy control in conjunction

with modeling and planning techniques to provide

reactive guidance of their robot. Sonar is used by

robot to construct a cellular map of its environment.

Sugeno developed a fuzzy control system for a

model car capable of driving inside a fenced-in

track. Ultrasonic sensors mounted on a pivoting

frame measured the car’s orientation and distance to

the fences. Fuzzy rules were used to guide the car

parallel to the fence and turn corners (Sugeno et al.,

1989).

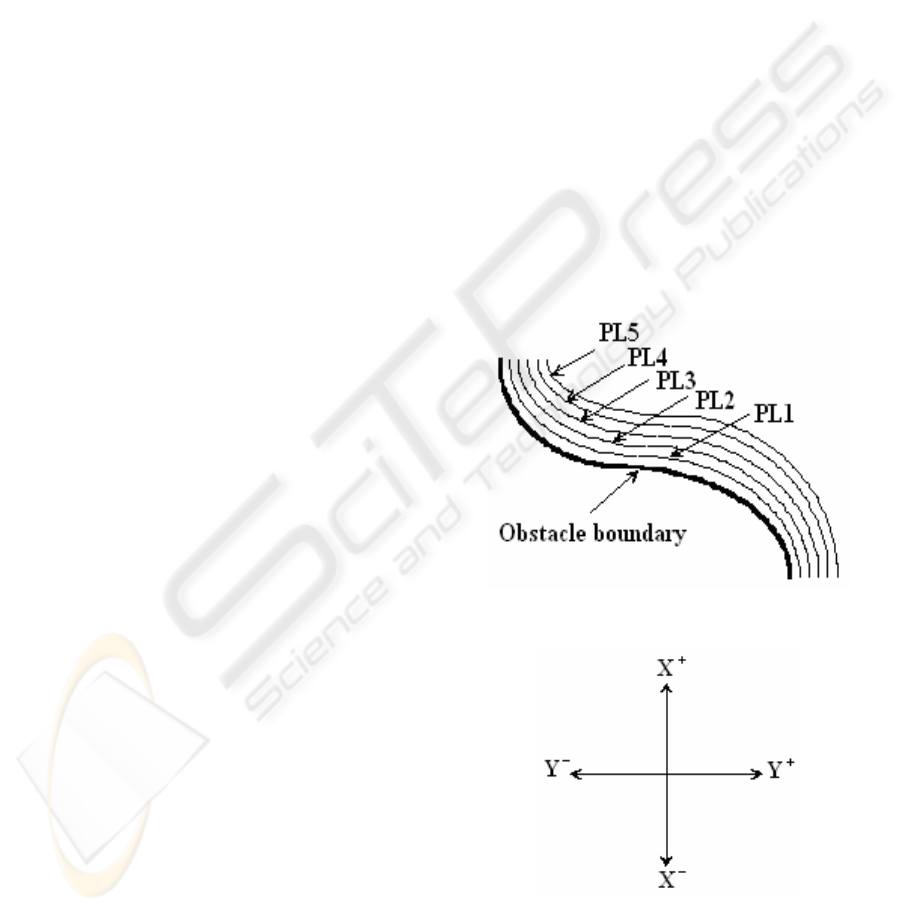
a) The proximity levels.

b) The two degrees of freedom of the locomotion system

of the mobile robot.

Figure 1: The proximity levels and the degrees of freedom

of the robot motion.

244

Stoian V. and Pana C. (2007).

FUZZY LOGIC ALGORITHM FOR MOBILE ROBOT CONTROL.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 244-247

DOI: 10.5220/0001633002440247

 SciTePress

2 CONTROL ALGORITHM

The mobile robot is equipped with a sensorial

system to measure the distance between the robot

and object that permits to detect 5 proximity levels

(PL): PL1, PL2, PL3, PL4, and PL5. Figure 1a

presents the obstacle (object) boundary and the five

proximity levels and Figure 1b presents the two

degrees of freedom of the locomotion system of the

mobile robot. This can move either on the two

rectangular directions or on the diagonals (if the two

degrees of freedom work instantaneous).

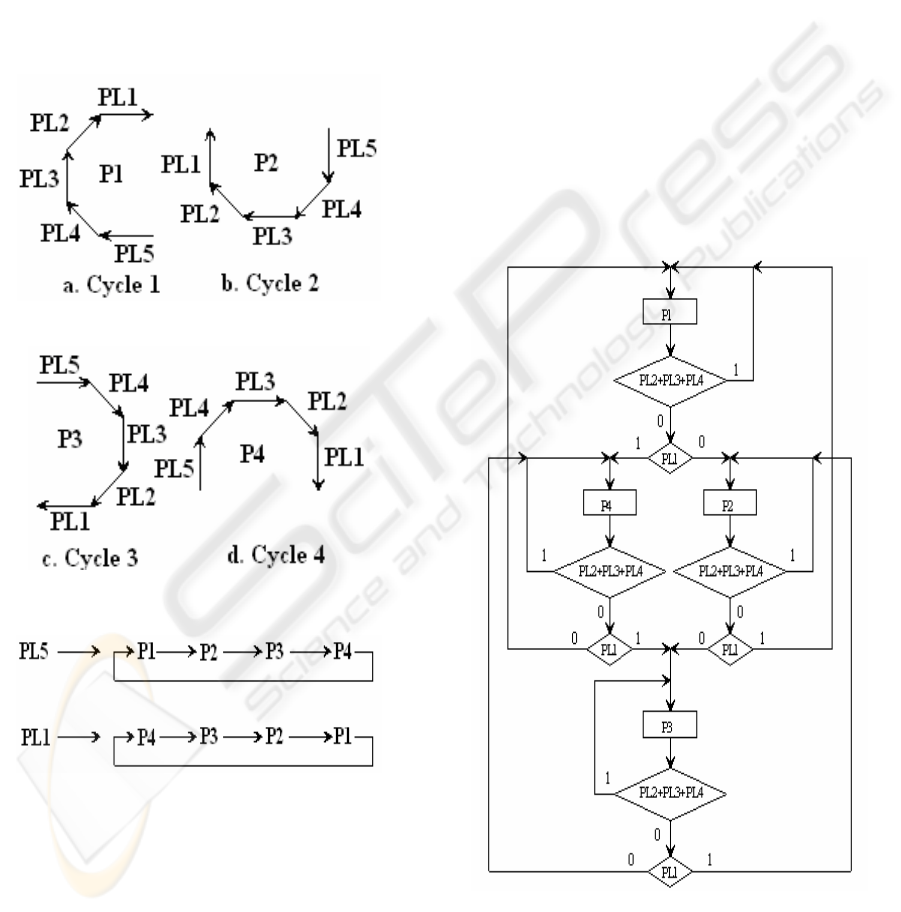
2.1) Motion cycles (programs)

2.2) The sequence of the programs

Figure 2: The sequences of the motion.

The goal of the proposed control algorithm is to

move the robot near the object boundary with

collision avoidance. Figure 2a shows four motion

cycles (programs) which are followed by the mobile

robot on the trajectory (P1, P2, P3, and P4). Inside

every cycle are presented the directions of the

movements (with arrows) for every reached

proximity level. For example, if the mobile robot is

moving inside first motion cycle (cycle 1 or program

P1) and is reached PL3, the direction is on Y-axis

(sense plus) (see Figure 1b, too). In Figure 2b we

can see the sequence of the programs.

One program is changed when are reached the

proximity levels PL1 or PL5. If PL5 is reached the

order of changing is: P1ÆP2ÆP3ÆP4Æ P1Æ

If PL1 is reached the sequence of changing

becomes: P4ÆP3ÆP2ÆP1Æ P4Æ

The motion control algorithm is presented in

Figure 3 by a flowchart of the evolution of the

functional cycles (programs). We can see that if

inside a program the proximity levels PL2, PL3 or

PL4 are reached, the program is not changed. If PL1

or PL5 proximity levels are reached, the program is

changed. The flowchart is built on the base of the

rules presented in Figure 2.1 and Figure 2.2.

Figure 3: The flowchart of the evolution of the functional

cycles (programs).

FUZZY LOGIC ALGORITHM FOR MOBILE ROBOT CONTROL

245

Figure 4: The inputs and outputs of the fuzzy algorithm.

3 FUZZY ALGORITHM

a) Membership functions of the proximity levels (distance)

measured with the sensors

b) Membership functions of the angle (the programs)

c) Membership functions of the X comands

d) Membership functions of the Y comands

Figure 5: Membership functions of the I/O variables.

The fuzzy controller for the mobile robots based

on the algorithm presented above is simple. Most

fuzzy control applications, such as servo controllers,

feature only two or three inputs to the rule base. This

makes the control surface simple enough for the

programmer to define explicitly with the fuzzy rules.

The above robot example uses this principle, in

order to explore the feasibility of using fuzzy control

for its tasks. Figure 4 presents the inputs (distance-

proximity levels and the program on k step) and the

outputs (movement on X and Y-axes and the

program on k+1 step) of the fuzzy algorithm.

For the linguistic variable “distance proximity

level” we establish to follow five linguistic terms:

“VS-very small”, “S-small”, “M-medium”, “B-big”,

and “VB-very big”. Figure 5a shows the

membership functions of the proximity levels

(distance) measured with the sensors and Figure 5b

shows the membership functions of the angle (the

programs). If the object is like a circle every

program is proper for a quarter of the circle.

Figure 5c and Figure 5d present the membership

functions of the X, respectively Y commands

(linguistic variables). The linguistic terms are: NX-

negative X, ZX-zero X, PX-positive X, and NY, ZY,

PY respectively.

Table 1: Fuzzy rules for evolution of the programs.

VS S M B VB

P1 P4 P1 P1 P1 P2

P2 P1 P2 P2 P2 P3

P3 P2 P3 P3 P3 P4

P4 P3 P4 P4 P4 P1

Table 2: Fuzzy rules for the motion on X-axis.

VS S M B VB

P1 PX PX ZX NX NX

P2 ZX NX NX NX ZX

P3 NX NX ZX PX PX

P4 ZX PX PX PX ZX

Table 3: Fuzzy rules for the motion on Y-axis.

VS S M B VB

P1 ZY PY PY PY ZY

P2 PY PY ZY NY NY

P3 ZY NY NY NY ZY

P4 NY NY ZY PY PY

Table 1 describes the fuzzy rules for evolution

(transition) of the programs and Table 2 and Table 3

describe the fuzzy rules for the motion on X-axis

and Y-axis, respectively. Table 1 implements the

sequence of the programs (see Figure 2.2 and Figure

3) and Table 2 and Table 3 implement the motion

cycles (see Figure 2.1 and Figure 3).

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

246

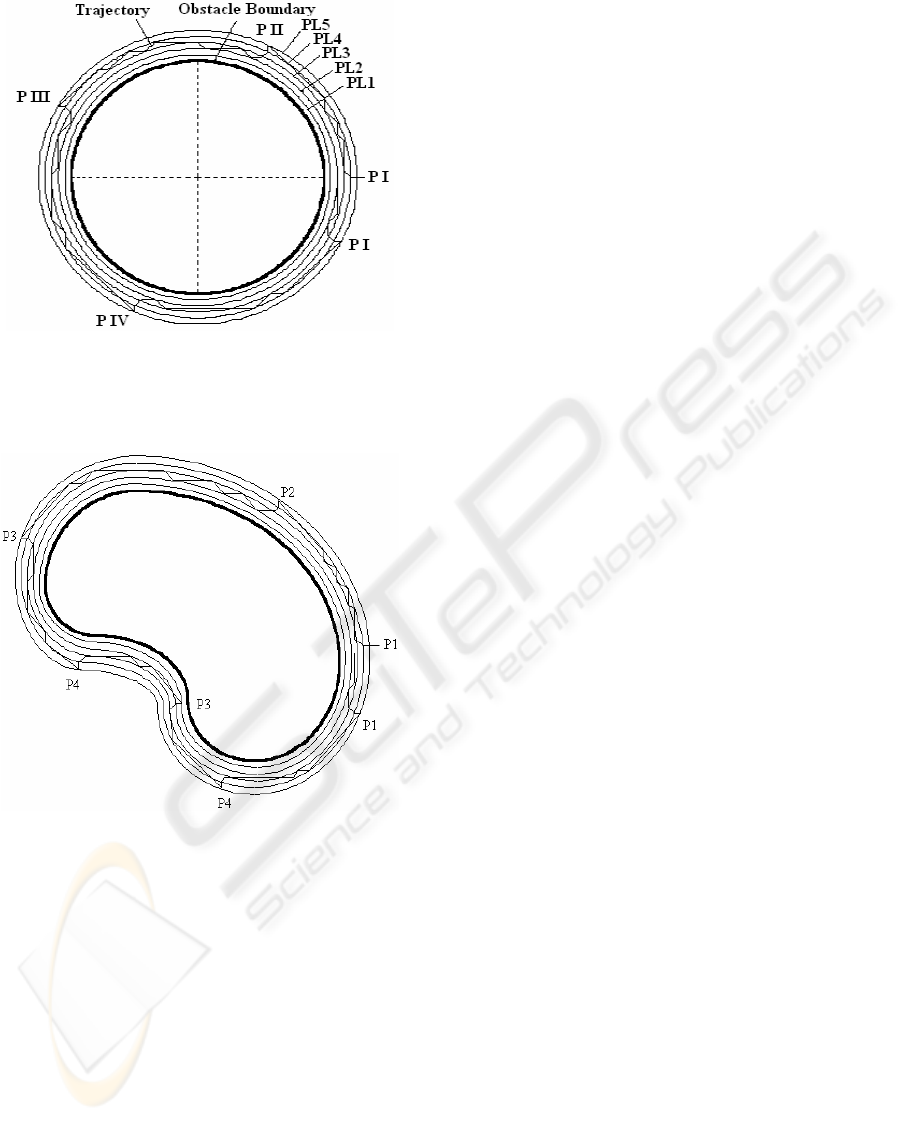
Figure 6: The trajectory of the mobile robot around a

circular obstacle.

Figure 7: The trajectory of the mobile robot around a

irregular obstacle.

4 SIMULATIONS

In the simulations can be seen the mobile robot

trajectory around an obstacle (object) with circular

boundaries (Figure 6) and around an obstacle

(object) with irregular boundaries (Figure 7). One

program is changed when are reached the proximity

levels PL1 or PL5. If PL5 is reached the order of

changing becomes as follows: P1ÆP2ÆP3ÆP4Æ...

If PL1 is reached the order of changing is becomes

follows: P4ÆP3ÆP2ÆP1Æ P4Æ ……

5 CONCLUSIONS

This paper presents a fuzzy control algorithm for

mobile robots which are moving next to the obstacle

boundaries, avoiding the collisions with them. Four

motion cycles (programs) depending on the

proximity levels and followed by the mobile robot

on the trajectory (P1, P2, P3, and P4) are shown.

The directions of the movements corresponding to

every cycle, for every reached proximity level are

presented. The sequence of the programs depending

on the reached proximity levels is indicated. The

motion control algorithm is presented by a flowchart

showing the evolution of the functional cycles

(programs). The fuzzy rules for evolution

(transition) of the programs and for the motion on X-

axis and Y-axis respectively are described. The

fuzzy controller for the mobile robots based on the

algorithm presented above is simple. Finally, some

simulations are presented. If the object is like a

circle, every program is proper for a quarter of the

circle.

REFERENCES

Zadeh, L. A., 1965. Fuzzy Sets, Information and Control,

No 8, pp. 338-353.

Sugeno, M., Murofushi, T., Mori, T., Tatematasu, T., and

Tanaka, J., 1989. Fuzzy Algorithmic Control of a

Model Car by Oral Instructions, Fuzzy Sets and

Systems, No. 32, pp. 207-219.

Song, K.Y. and Tai, J. C., 1992. Fuzzy Navigation of a

Mobile Robot, Proceedings of the 1992 IEEE/RSJ

Intern. Conference on Intelligent Robots and Systems,

Raleigh, North Carolina.

Khatib, O., 1986. Real-Time Obstacle Avoidance for

Manipulators and Mobile Robots, International

Journal of Robotics Research, Vol. 5, No.1, pp. 90-98.

Boreinstein, J. and Koren, Y., 1989. Real-time Obstacle

Avoidance for Fast Mobile Robots, IEEE Transactions

on Systems, Man., and Cybernetics, Vol. 19, No. 5,

Sept/Oct. pp. 1179-1187.

Jamshidi, M., Vadiee, N. and Ross, T. J., 1993. Fuzzy

Logic and Control. Software and Hardware

Applications, PTR, Prentice Hall, New Jersey, USA.

Yan, J., Ryan, M., and Power, J., 1994. Using Fuzzy

Logic. Towards intelligent systems, Prentice Hall, New

York.

FUZZY LOGIC ALGORITHM FOR MOBILE ROBOT CONTROL

247