
GRASP CONFIGURATION MATCHING
Using Visual and Tactile Sensor Information
Madjid Boudaba
Design Center
TES Electonic Solution GmbH, Zettachring 8, 70567 Stuttgart, Germany
Alicia Casals
GRINS: Research Group on Intelligent Robots and Systems
Technical University of Catalonia, Pau Gargallo 5, 08028 Barcelona, Spain
Keywords:
Visual image, Tactile image, Grasp planning, Block matching algorithm.
Abstract:
Finding the global shape of a grasped object directly from touch is time consuming and not highly reliable.
This paper describes the relationship between visual features and grasp planning, and correlates visual and tac-
tile information for a better description of the object’s shape and grasping points determination. The grasping
process proposed is experimented with a three fingered robotic hand.
1 INTRODUCTION
Grasping has been an active area of robotics research
in the last decades. Although a great number of
sensory systems have been used to monitor and to
control grasping, their usefulness is often limited
by the ability of handling all aspects of detec-
tion/recognition, guidance, alignment and grasping.
To place our approach in perspective, we review
existing methods for sensor based grasp planning.
The existing literature can be broadly classified into
two categories; vision based and tactile based. For
both categories, the extracted image features are of
concern, they can range from geometric primitives
such as edges, lines, vertices, and circles to optical
flow estimates. The first category uses image features
to estimate the robot’s motion with respect to the
object pose (Maekawa et al., 1995), (Smith and
Papanikolopoulos, 1996), (Allen et al., 1999). Once
the robot hands is already aligned with the object,
then, it only needs to know where the fingers are
placed on the object. The second category of sensor
uses image features to estimate the touch sensing
area in contact with the object (Berger and Khosla,
1991), (Chen et al., 1995), (Lee and Nicholls, 1999).
A practical drawback is that the grasp execution
is hardly reactive to sensing errors such as finger
positioning errors. A vision sensor, meanwhile,
is unable to handle occlusions. Since an object is
grasped according to its CAD model (Kragic et al.,
2001), an image also contains redundant information
that could become a source of errors and inefficient
in the processing.
This paper is an extension of our previous work
(Boudaba et al., 2005) and (Boudaba and Casals,
2006) on grasp planning using visual features. In
this work, we demonstrate its utility in the context of
grasp (or fingers) positioning. Consider the problem
of selecting and executing a grasp. In most tasks,
one can expect various uncertainties. Grasping an
object implies building a relationship between the
robot hand and the object model. The latter is often
unavailable or poorly known. Thus, selecting a grasp
position from such model can be unprecise or unprac-
ticable in real time applications. In our approach, we
avoid using any object model and instead we work
directly from edge features. In order to avoid fingers
positioning errors, a sizable image blocks are defined
that represent the features of grasping contact points.
This not only avoids detection/localization errors
but also saves computation effort that could affect
the reliability of the system. Our features matching
based approach can play the critical role of forcing
the fingers to move to the desired positions before
the task of grasping is executed. To achieve a high
level of matching efficiency, the visual image is first
divided into squared blocks of pixels. Then for each
one of these blocks the algorithm tries to find its
correspondence in the target block that is the closest
117
Boudaba M. and Casals A. (2007).
GRASP CONFIGURATION MATCHING - Using Visual and Tactile Sensor Information.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 117-124
DOI: 10.5220/0001633401170124
Copyright
c
SciTePress

to it according to a predetermined criterion. Finally,
we reduce or eliminate redundant information con-
tained in the image by transforming the result of the
matching algorithm to the frequency domain. Then a
compression scheme is proposed to the image coding.
The proposed work is divided into two phases:
1. Grasp planning phase: For each two-
dimensional view of an object in a visual
frame features of its contour are calculated.
These features are then used as input data, both
for the grasp planning and features matching
phases. The grasping positions are generated
in the planning task, so a relationship between
visual features and grasp planning is proposed.
Then a set of geometrical functions is analysed to
find a feasible solution for grasping. The result of
grasp planning is a database containing a set of
valid grasps, the most favorable as well as those
rejected.
2. Sensor features matching phase: Unlike vision
which provides global features of the object, tac-
tile sensor provides local features when the fin-
gertip is in touch with the object. In order to iden-
tify and locate the features that best fit the two
domains (vision and touch) of features, a contour
splitting process divides the object’s contour into
blocks, so that different matching techniques can
be applied. For the purpose of features match-
ing, extracting edge features are of concern using
the basic results from different approaches. The
matching is conducted in two-dimensional space.
Each edge in the block is treated as features.
2 GRASP BACKGROUND
Geometric formulation and grasp feasibility are re-
viewed and discussed based on (Hirai, 2002). Given
a grasp which is characterized by a set of contact
points and the associated contact models, the problem
is determining whether the grasp has a force-closure.
For finger contact, a commonly used model is point
contact with friction (PCWF). In this model, fingers
can exert any force pointing into the friction cone at
the edge of contacts (We use edge contact instead
of point contact, which can be described as a linear
combination of two vectors, see Figure 1(b)). To
fully analyze grasp feasibility, we need to examine
the full space of forces acting on the object. Forming
the convex hull of this space is difficult due to the
nonlinear friction cone constraints imposed by the
contact models. In this section, we only focus in
precision grasps, where only the fingertips are in
contact with the object. After discussing the friction
cone modeling, a formalizme is used to analyze force
closure grasps using the theory of polyhedral convex
cones.
i
C
Q
(a)
3
u
2
u
1
u
i
C
ci
v
1
x
2
x
i
g
i
l
(b)
CCW
Figure 1: Friction cone modelleing.
2.1 Friction Cone Modelling
For the analysis of the contact forces in planar grasps,
we simplify the problem by linearizing the friction
cone by a polyhedral convex cone. In the plane, a
cone has the appareance shown in Figure 1(b). This
means that we can reduce the number of cone sides,
m=6 to one face.
Let’s denote by P, the convex polytopes of a face
cone, and
{
u
1
, u
2
, u
3
}
its three representative vertices.
We can define such polytopes by
P =
(
x =
3
∑
i=1
δ
i
u
i
: 0 ≤ δ
i
≤ 1,
3
∑
i=1
δ
i
= 1
)
(1)
2.2 Grasp Space Evaluation
The full space of a grasp is evaluated by analysing its
convex hull. For a set of friction cone intersections,
the full space can be defined by
C
k
1
= C(P
1
) ∩C(P
2
) ∩C(P
k
) (2)
where k is the number of grasping contacts. Note
that the result of C
k
1
is a set of friction cone intersec-
tions and produces either an empty set or a bounded
convex polytope. Therefore, the solution of (2) can be
expressed in terms of its extreme vertices
Ω
v
p
1
(U) =
(
v
p
∑
i=1
α
i
u
ci
,
v
p
∑
i=1
α
i
= 1, α
i
≥ 0
)
(3)
where v
p
is the total number of extreme vertices.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
118

Figure 2 illustrates an example of feasible solu-
tion of Ω
v
p
1
(U) and its grasp space represented by its
extreme vertices P =
{
v
1
, v
2
, ..., v
5
}
.
2
n
3
n
1
n
Three friction cones intersection:
Grasping
Region
1
f
2
f
3
f
(a)
1
C
2
C
3
C
3
1
C
(b)
1
x
2
x
1
v
2
v
3
v
4
v
5
v
Convex polytope: P
Figure 2: Feasible solution of a three-fingered grasp.
3 FEATURES-BASED GRASPING
In robotic grasping tasks, when several input sensors
are available simultaneously, it is generally necessary
to precisely analyze all the data along the entire
grasping task. We can acquire the precise position
and orientation of the target object and robot hand
motion from a vision system and can acquire force,
torque, and touch information from tactile sensing.
The object being extracted from a video sequence
requires encoding its contour individually in a
layered manner and provide at the receiver’s side
an enhanced accessibility of visual information.
In the same way, for the object being extracted
from a tactile sensor, the tactile layer processes
and provides the tactile information at its receiver’s
side. Obviously, the accuracy of this data is of signif-
icant importance for the eventual matching algorithm.
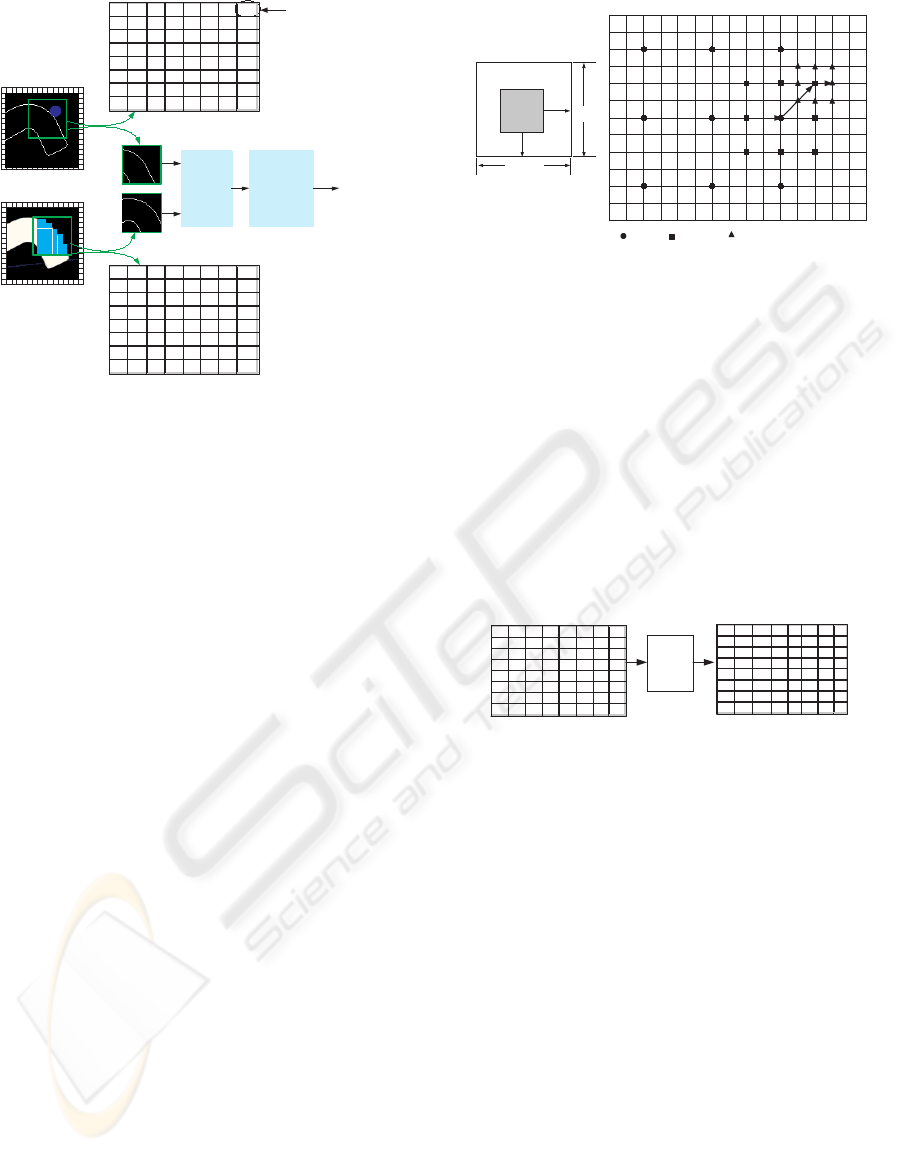
Figure 3 illustrates a layered composition of
a tactile and a vision sensor. Given as input two
consecutive images data S (tactile) and V (visual), the
success (or simply the completion time) of the task
depends on the level of processing efficiency.
3.1 Visual Features Extraction
Due to their semantically rich nature, contours are
one of the most commonly used shape descriptors,
and various methods for representing the contours
of 2D objects have been proposed in the literature
(Costa and Cesar, 2001). Extracting meaningful
features from digital curves, finding lines or seg-
ments in an image is highly significant in grasping
applications. Most of the available methods are
variations of the dominant point detection algorithms
(M. Marji, 2003). The advantage of using dominant
Tactile Image Visual Image
Edge detection
and contour extraction
Edge detection
and contour extraction
Computation of line segments
Computation of line segments
Segment grouping
Contour approximation using
polygonal approximation
Tactile and Visual Features Matching.
Contour splitting into
macroblocks
Vision Layer
Tactile Layer
Image acquisition and processing
(V)
(S)
Figure 3: Tactile and visual features data processing.
points is that both, high data compression and feature
extraction can be achieved. Other works prefer the
method of polygonal approximation using linking
and merging algorithms (Rosin, 1997) and curvature
scale space (CSS).
We denote by V a function regrouping parameters
of visual features defined by
V =
{
vlist, slist, llist, com
}
(4)
where vlist and slist are the lists of consecutive
contour’s vertices and segments, respectively. llist
is a list containing the parameters of segments,
calculated with respect to the object’s center of mass,
com. The resulting parameters of V fully describe
the two-dimensional location of features with respect
to the image plane. The visual features obtained can
be used as input data for both, grasp planning and
features matching for grasp control.
Figure 4: Visual features extraction.
3.2 Tactile Features Extraction
Unlike vision which provides global features of the
object, tactile sensor provides local features when the
fingertip is in touch with the object. To simplify the
problem, tactile features are treated as visual features
using the basic results from different approaches (Lee
GRASP CONFIGURATION MATCHING - Using Visual and Tactile Sensor Information
119

and Nicholls, 1999). For the purpose of sensor fea-
tures matching, extracting edge features are of inter-
est. Figure 5 illustrates three examples of tactile sen-
sor in touch with the object. From left to right side,
the sensitive area is shown with hashed region and lo-
cated at upper corner side, bottom side and covering
the entire object area, respectively. The tactile sensor
device consists of a printed circuit board with a tactile
array of electrodes (called tactels) on its surface and
circuitry to deliver the tactile data of local features
extracted from the sensing elements, as well as circu-
ity to monitor and adjust the power supply voltage to
the sensor. The raw data from the sensing elements is
processed and produces as output a vector S contain-
ing the parameters that define tactile features.
S =
{
elist, slist, plist
}
(5)
where elist and slist are list of consecutive con-
tour edges and segments, respectively. plist is a list
containing the parameters tied to segments, such as
location and orientation in the tactile sensor plane.
Sensitive areaObject area
Figure 5: Sensitive area of the tactile sensor. This infor-
mation can be determined by examination of the frequency
domain, and is shown in Figure 10.
4 GRASP PLANNING
Grasp planning can be seen as constructing proce-
dures for placing point contacts on the surface of a
given object to achieve force-closure grasps. Tak-
ing as input the set of visual features extracted from
the contour of the object, the output is a set of valid
grasps. The relationship between visual features and
grasp planning is given in the next section.
4.1 Grasp Point Generation
Generating a number of valid grasps from a list of
candidates and classifying the best among them is
quite time consuming. Thus a preprocessing (or pre-
filtering) is necessary before the grasping points gen-
eration takes place. A fingertip is estimated to be as a
sphere with radius f
r
(see Figure. 2(b)), a grasping re-
gion must be large enough for placing contact points
on it. Hence, a prefiltering is applied to the list, slist
defined in (4) to discard those segments with length
less than the diameter of the sphere (s
i
< 2f
r
). Fig-
ure. 4 illustrates the result of prefiltering processes as
described by the following equation:
glist =
{
g
1
, g
2
, ··· , g
m
}
(6)
where glist is a linked list of grasping regions and
m its number.
A very important aspect of (6) is the way how
knowledge about grasping regions are represented in
the extraction process, knowledge that will be used
for generating grasping points.
The following equation describes the relationship
between the visual features and grasp planning
G = f(glist, gparam, com) (7)
where glist, gparam, and com are the visual fea-
tures observed on the image plane and G is a grasp
map of outputs defined by the relationship between
fingers and the location of contact points on its cor-
responding grasping regions. From the grasp map G
three possible solutions are derived:
G :
G
s
=
{
G
s
1
, G
s
2
, ··· , G
s
is
}
G
b
=
G
b
1
, G
b
2
, ··· , G
b
ib
G
r
=
{
G
r
1
, G
r
2
, ··· , G
r
ir
}
(8)
where G
s
, G
b
, and G
r
are selected, best, and
rejected grasp, respectively. The is, ib, and ir are
the number of selected, best, and rejected grasps,
respectively.
For a three-finger grasps, the selected grasps (G
s
)
are given in the following form:
G
s
:
G
s
1
=
{
( f
1
, g
1
), ( f
2
, g
6
), ( f
3
, g
9
)
}
G
s
2
=
{
( f
1
, g
2
), ( f
2
, g
6
), ( f
3
, g
10
)
}
.
.
.
G
s
is
=
{
( f
1
, g
1
), ( f
2
, g
8
), ( f
3
, g
12
)
}
where f
i
and g
i
are the i −th finger and grasping
region, respectively.
A similar form can be given for representing the
best grasps G
b
and those rejected G
r
.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
120

4.2 Algorithm
The grasp planning algorithm is divided into several
procedures and operates as follows:
1. Visual features procedure
• Function grouping visual features using (4)
2. Grasping point generation procedure
• Pick three grasp regions from (6)
• Determine the initial position of f
1
, f
2
and f
3
• Compute their friction cones using (1)
• Compute the friction cones intersection of (2)
3. Grasping test procedure
• Compute the solution friction cones using (3)
• Check whether the polytopes given by (3) is
bounded. If so, stop and save the selected
grasps to G
s
.
• Else save the rejected grasps to G
r
.
4. Quality test procedure
• The last step of the algorithm consists of select-
ing the best grasps from a range of valid grasps
from lower to upper acceptance measures by
using the parameters measure given in table 1.
Save to G
b
.
5 FEATURES MATCHING
Our goal is to match the grasping positions correspon-
dence between the visual and tactile sensor features.
The matching process works first getting a grasping
position within its searching area and next it updates
the tactile features using a tactile sensor. The size of
the search windows is very important when configur-
ing a matching process. The larger the search window,
the longer it takes to process the search. The match-
ing is conducted in the pixel domain, so the contrast
is necessary for identifying edges in reference (visual)
and target (tactile) image. Images with weak contrast
should be avoided since the matching algorithm uses
the edges based searching. The weaker the contrast,
the less the amount and accuracy of edge-based infor-
mation with which the searching is performed. Fig-
ure 7 shows two tables in grayscale values assigned
to each block of matching.
5.1 Image Subregions
In order to identify the location of the best fitting
between the tactile sensor frames and visual frames,
a subregion process is performed that scales down
the contour image into subregions in an efficient
way so that the matching algorithm can be applied.
The basic principle is similar to the image (or video)
compression techniques, which defines how the
component (RGB, YUV or YCrCb) can be down-
sampled and digitalised to form discrete pixels. The
terms 4:2:2 and 4:2:0 are often used to describe the
sampling structure of the digital image. 4:2:2 means
the chrominance is horizontally sub-sampled by a
factor of two relative to the luminance; 4:2:0 means
the chrominance is horizontally and vertically sub-
sampled by a factor of two relative to the luminance.
In the case of a 704x576 PAL/SECAM standard for
example, the QCIF (Quarter Common Immediate
Format) can be obtained by scaling down the image
with a factor of 4 in the horizontal/vertical direction.
For a QCIF format of size 176x144, there are 25.344
pixels in the frame. A macro block defines a 16x16
pixel area (256 pixels), so there are 99 macro blocks
to process (see Figure. 6).
Macro Block (MB)
16x16 pixels
Object contour:
QCIF: 176 x 144 pixels
Figure 6: Image subregions.
5.2 Block-Matching Algorithm
The Mean Absolute Difference (MAD) is a well
known matching criteria and widely used due to its
lower computational complexity (Lu and Liou, 1997).
Given two blocks represented by two set of features:
S =
a
1
, a
2
, ..., a
q
andV =
b
1
, b
2
, ..., b
q
, the corre-
sponding features from each block are compared and
their differences accumulated, as described by equa-
tion
MAD(dx, dy) =
1
N
2
N
∑
i=1
N
∑
j=1
|
V [i, j] − S[i+ dx, j + dy]
|
(9)
where S(i, j) represents a (N×N) macroblock of
pixel intensity in the target frame and V(i, j) repre-
sents (N×N) macroblock of pixel intensity in the ref-
erence frame. (dx, dy) is a vector representing the
GRASP CONFIGURATION MATCHING - Using Visual and Tactile Sensor Information
121
Reference
Target
Mean
Absolute
Difference
(MAD)
Image
Difference
Coding (IDC)
2
)00011000(24
Pixels valaues (0~255)
12 14 27 35 19 14 24 10
9 4 45 28 49 20 24 30
1 35 15 42 49 20 24 42
16 30 17 44 35 28 28 21
20 26 13 14 16 25 35 14
26 20 18 18 17 17 15 21
40 49 19 35 28 15 15 10
20 18 19 21 18 44 10 5
42 14 27 35 49 44 30 24
49 49 35 28 49 20 24 30
21 35 35 42 42 28 28 42
56 70 77 84 95 28 28 21
70 26 13 14 16 95 35 14
26 20 18 18 17 17 35 21
40 49 49 35 28 35 35 35
20 18 24 21 18 84 21 21
Pixels valaues (0~255)
Bitstream output
Figure 7: Block matching algorithm.
search area. For our application the search area is
specified by dx = (−p, p) and dy = (−p, p) where
p = 6 and N = 16.
The matching of a macroblock with another is
based on the output of a cost function (9). The mac-
roblock that results in the least cost is the one that
matches the closest to current macroblock, Figure 7.
For each fingertip that gets in touch with the object,
the tactile features are matched to those of visual fea-
tures inside a predefined searching area. A motion
vector is then applied to search the features correspon-
dence between blocks in the target frame and those in
the reference frame. Figure 8 illustrates the searching
method that evaluates the MAD cost function within
the search area. Many other search methods can be
found in (Furht, 1995).
5.3 Image Difference Coding
In order to control the grasping position, the result of
the matching algorithm can be defined as error posi-
tion or that so called error grasp, is then calculated
using the following expression:
G
e
(i, j) = V(i, j) − S(i+ dx, j + dy) (10)
Since we want to guide the robot hand towards
these grasping references G
ref
, the solution consists
of reducing the grasp error G
e
by moving the tactile
sensors towards the set of corresponding positions
of grasping references. The cost of a solution is
expressed as the total sum of contact displacements
over the surface of the object from an initial contact
configuration. If the result of matching is outside a
given margin, then the grasp controller should launch
a new measurement via joint angle and position
First step
second step
third step
v
Searching vector
v
Searching area (2p+N)x(2p+N)
Current
MacroBlock
16
16
Searching area (2p+N)x(2p+N)
p=6
p=6
2p + N
2p + N
Figure 8: Searching area.
sensors.
The result of block matching algorithm (see
Figure 8) is a two-dimensional vector called motion
vector, v(l, m). The Image Difference Coding (IDC)
processes these measurements and produces as output
a vector image containing the parameters of grasping
positions, which are compressed in a suitable format
to reduce the data transmission bandwidth. The
digital cosine transform (DCT) is used due to its
capability of removing spatial redundancy to achieve
low bit rates.
42 28 20 35 49 24 24 30
49 49 35 28 49 20 24 30
21 35 35 42 42 28 28 42
56 70 77 84 95 28 28 21
70 12 33 47 61 95 35 14
26 20 18 18 75 75 35 21
40 49 49 35 28 35 35 35
20 18 45 21 82 84 21 21
DCT
70 24 -28 -4 -2 -10 -1 0
-53 -35 43 13 7 13 1 3
23 9 -10 -8 -7 -6 5 -3
6 2 -2 8 2 -1 0 -1
-10 -2 -1 -12 2 1 -1 4
3 0 0 11 -4 -1 5 6
-3 -5 -5 -4 3 2 -3 5
3 0 4 5 1 2 1 0
),( mlv ),( vug
Figure 9: DCT Image compression.
The DCT transforms each 8x8 block of greyscale
values into a block of 8x8 spectral frequency coeffi-
cients. The energy tends to be concentrated into few
significant coefficients. Other coefficients are close to
zero and insignificant (see Figure 9).
Next step of IDC is to compress the frequency do-
main, by not transmitting (or not coding) the close-
zero coefficient (insignificant coefficients) and by
quantizing and coding the remaining coefficients.
6 EXPERIMENTAL RESULTS
Figure 10 illustrates our experimental system which
consists of a anthropomorphic robot hand equipped
with a tactile array sensor on each fingertip and a
stereo vision system. The spacial resolution of the
tactile sensor has 256 (16x16) sensing cells over an
area of 100 square millimeter. The sensory data pro-
cessing were performed using MCAGUI and SVS
tools for tactile and vision data, respectively, devel-
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
122

oped at the Institute of Process Control and Robotics
(Boudaba et al., 2005). Figure 10(b) shows the tac-
tile sensor response frames. Every cell of the sensing
matrix is sampled at 10 frames per second. Figure 11
and Figure 12 show the result of five grasp configura-
tions and Table 1 resumes their parameter measures.
d
1
, d
2
and d
3
are distance measures of finger posi-
tion f
1
, f
2
and f
3
from the object’s center of mass.
x
1
x
2
are the coordinates of the focus point F in the
plane. d is the measured distance between focus point
and center of mass. R is the vector radius of the ball
centered at F. The object center of mass is located
at com = (121.000, 98.000. The angle of the friction
cone, α= 17.000 for all configurations. We have im-
plemented the grasp planning algorithms in Matlab
environment for computing feasible grasping regions
for three-finger hands.
(b1) Full frame
(b2) Individual frame
(a) Three fingers hand in contact with the object
Figure 10: Tactile sensor response frames.
7 CONCLUSION
A framework to discuss sensor frames matching us-
ing tactile and visual features is presented in this pa-
per. As a new approach to the grasp planning prob-
lem, the idea of vision-based grasping has been ex-
plored, within the specific context of using visual fea-
tures relevant to the grasping and manipulation tasks,
as complementary information to tactile data. In or-
(a) (b)
(c) (d)
Figure 11: Grasp planning setup.
Table 1: Parameter measures of five grasp configurations.
obj =
{
GC1, GC2, GC3, GC4, GC5
}
d
1
d
2
d
3
F(x
1
, x
2
) d R
86.80 63.70 35.52 119.97 96.95 1.80 7.94
86.80 33.82 65.99 118.41 96.69 2.98 9.37
24.47 86.80 23.82 99.19 122.88 32.53 2.44
23.82 33.82 71.22 127.26 102.97 7.88 5.34
81.51 65.99 35.52 114.59 84.46 15.39 4.49
der to provide a suitable description of object con-
tour, a method for grouping visual features has been
proposed. Then a function defining the relationship
between visual features and grasp planning has been
described. A very important aspect of this method is
the way knowledge about grasping regions are rep-
resented in the extraction process, which excluded
all undesirable grasping points (unstable points) and
all line segments that do not fit to the fingertip posi-
tion. This filtering process has been used to reduce the
time consumption during the process of determining
suitable grasping points. For extracting the local fea-
tures of the curves representing the object contour, the
solution adopted is a polygonal approximation using
a linking/merging algorithms.Then the force-closure
condition is applied to evaluate grasping points deter-
mination. The method implemented here is currently
restricted to any kind of 2D objects. In a future work,
it is intended to extend our method to 3D object.The
object therefore needs to be seen from different points
of view which is desirable for grasp planning that per-
forms well in the real world.
GRASP CONFIGURATION MATCHING - Using Visual and Tactile Sensor Information
123

(a) (b)
(c) (d)
(a) Grasp Configuration(GC): 2-3
(c) (d)
(a)
(b)
(b) Grasp Configuration(GC): 4-5
Figure 12: Result of Grasp planning with three-fingered Grasps.
ACKNOWLEDGEMENTS
The authors would like to thank Prof. Dr. H. Wo-
ern and his co-workers from the IPR institute for
their support in providing the facilities and the an-
thropomorphic robot hand for testing the proposed ap-
proach.
REFERENCES
Allen, P., Miller, A., Oh, P., and Leibowitz, B. (1999). Inte-
gration vision, force and tactile sensing for grasping.
Int. Journal of Intell. Mechatronics, 4(1):129–149.
Berger, A. D. and Khosla, P. K. (1991). Using tactile data
for real-time feedback. International Journal of of
Robotics Research (IJR’91), 2(10):88–102.
Boudaba, M. and Casals, A. (2006). Grasping of planar
obbjects using visual perception. In Proc. IEEE 6th
International Conference on Humanoid Robots (HU-
MANOIDS’06), pages 605–611, Genova, Italy.
Boudaba, M., Casals, A., Osswald, D., and Woern, H.
(2005). Vision-based grasping point determination
on objects grasping by multifingered hands. In Proc.
IEEE 6th International Conference on Field and Ser-
vice Robotics (FRS’05), pages 261–272, Australia.
Chen, N., Rink, R. E., and Zhang, H. (1995). Edge track-
ing using tactile servo. In Proc. IEEE/RSJ Interna-
tional Conference on Intelligent Robots and Systems
(IROS’95), pages 84–99.
Costa, L. and Cesar, R. (2001). Shape Analysis and Clas-
sification Theory and Practice. CRC Press, Florida,
USA, 1st edition.
Furht, B. (1995). A survey of multimedia compression
techniques and standards, part ii: Video compression.
Real-Time Imaging Journal, 1:319–337.
Hirai, S. (2002). Kinematics of manipulation using the the-
ory of polyhedral convex cones and its application to
grasping and assembly operations. Trans. of the Soci-
ety of Inst. and Control Eng., 2:10–17.
Kragic, D., Miller, A., and Allen, P. (2001). Real-time
tracking meets online grasp planning. In Proc. IEEE
International Conference on Robotics and Automata-
tion (ICRA’2001), pages 2460–2465, Seoul, Korea.
Lee, M. H. and Nicholls, H. R. (1999). Tactile sensing for
mechatronics - a state of the art servey. Mechatronics,
9:1–31.
Lu, J. and Liou, M. L. (1997). A simple and efficient
search algorithm for block matching motion estima-
tion. IEEE Trans. Circuits And Systems for Video
Technology, 7:429–433.
M. Marji, P. S. (2003). A new algorithm for dominant points
detection and polygonization of digital curves. Jour-
nal of the Pattern Recognition Society, 36:2239–2251.
Maekawa, H., Tanie, K., and Komoriya, K. (1995). Tac-
tile sensor based manipulation of an unknown object
by a multifingered hand with rolling contact. In Proc.
IEEE International Conference on Robotics and Au-
tomatation (ICRA’95), pages 743–750.
Rosin, P. L. (1997). Techniques for assesing polygonal ap-
proximation of curves. IEEE Transaction on Pattern
Analysis and Machine Intelligence, 19:659–666.
Smith, C. and Papanikolopoulos (1996). Vision-guided
robotic grasping: Issues and experiments. In Proc.
IEEE International Conference on Robotics and Au-
tomatation (ICRA’96), pages 3203–3208.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
124
