A DISCRETE-EVENT SYSTEM APPROACH TO MULTI-AGENT

DISTRIBUTED CONTROL OF CONTAINER TERMINALS

Guido Maione

DEESD, Technical University of Bari, Viale del Turismo, 8 - 74100, Taranto, Italy

Keywords: Multi-Agent Systems, Discrete Event Systems, Container Terminals, Transport Systems.

Abstract: The area of modelling and controlling intermodal terminal systems is relatively new. The paradigms of

Discrete Event Systems for modelling and of Multi-Agent Systems (MAS) for distributed control seem

promising. Many research attempts developed modelling and simulation tools but no standard exists. This

paper presents a Discrete Event System model of the agents introduced to describe how a distributed control

of the terminal activities can be achieved. The interactions between four classes of agents are detailed. The

approach is useful to develop a simulation platform to test MAS efficiency in terminal management and to

measure the performance of static or adapted control strategies.

1 INTRODUCTION

Planning and scheduling resources in a maritime

container terminal pose very complex modelling and

control problems to the scientific community.

Flexible and powerful modelling and simulation

tools are necessary to describe an intermodal hub

system made up of many different infrastructures

and services. In the absence of standard tools,

several research studies are based on discrete event

simulation techniques (Vis and De Koster, 2003), on

mathematical models or empirical studies (Crainic et

al., 1993, Gambardella et al., 1998).

In the context of intelligent control of transport

systems, this paper uses the Discrete EVent System

(DEVS) specification technique (Zeigler et al.,

2000) to completely and unambiguously characterize

a Multi-Agent System (MAS) for controlling a

container terminal. Autonomous agents play as

atomic dynamic DEVS. They exchange messages

one with another to negotiate services in a common

environment. The DEVS approach leads to

heterarchical MAS where all information and

control functions are distributed across agents, and

allows rigorous theoretical analysis of structural

properties of the MAS. Moreover, the DEVS

formalism is an interesting alternative to other tools

for MAS specification (Huhns and Stephens, 2001,

Lin and Norrie, 2001). It is suitable to develop

models both for simulation and for implementation

of the software controllers.

As in MAS for manufacturing control (Heragu,

2002), agents can use decision algorithms based on a

fictitious currency to buy services from other seller

agents which use pricing strategies. Sellers and

buyers reach an equilibrium between conflicting

objectives, i.e. to maximize profit and to minimize

costs, respectively. Recent analytical models of

negotiation (Hsieh, 2004) underline the need of a

systematical analysis and validation method for

distributed networks of autonomous agents. Other

researches focus on the experimental and detailed

validation of MAS on distributed simulation

platforms (Shattenberg and Uhrmacher, 2001, Logan

and Theodoropoulos, 2001).

Here, a detailed DEVS model is developed for

the interactions between the agents concurrently

operating for the critical downloading process of

containers from a ship. This paper is a contribution

to define a complete DEVS model to develop a

simulation platform for testing and comparing the

proposed MAS with other distributed control

architectures for container terminals. The simulation

model could be used to design and test alternative

system layouts and different control policies, both in

standard and perturbed operating conditions.

The paper is organized as follows. Section 2

describes the main processes in a terminal. Then, the

basic components of the MAS are presented, and

their roles and relations are indicated. Section 3

models agents as atomic DEVS, and focuses on their

interactions when containers are downloaded from

300

Maione G. (2007).

A DISCRETE-EVENT SYSTEM APPROACH TO MULTI-AGENT DISTRIBUTED CONTROL OF CONTAINER TERMINALS.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 300-305

DOI: 10.5220/0001633603000305

 SciTePress

ships to the terminal yard. Section 4 gives some

ideas about the simulation platform to test efficiency

and robustness of the proposed MAS architecture.

Section 5 overviews the benefits of the approach and

enlightens open issues.

2 THE MAS FRAMEWORK FOR

CONTAINER TERMINALS

To define the autonomous agents operating and

interacting in a terminal environment, the main

terminal processes have to be abstracted. They are

commonly identified as import, export, and

transshipment cycles.

2.1 Import, Export and Transshipment

Cycles in a Container Terminal

Imported containers arrive on a vessel or feeder ship

and depart by trains/trucks. Exported containers

arrive by trains/trucks and depart on a vessel ship

(transition from railway/road to sea mode).

Transshipped containers arrive and depart by ship:

cargo is moved from vessel (feeder) to feeder

(vessel) ships for close (far) destinations.

Then, containers have to be: loaded/downloaded

on/from ships; delivered/picked to/from trucks or

trains; stacked and kept in blocks, in which the

terminal yard is divided; transferred from

ship/train/truck to blocks and backwards;

consolidated, i.e. redistributed between blocks to

allow fast retrieval. To this aim, several dedicated or

shared resources are used: quay cranes, yard cranes,

railway cranes; internal transport vehicles (trailers);

quays and berths, lanes for internal transport, gates,

railway tracks; skilled human operators.

A road import cycle follows three steps. Firstly,

quay cranes download containers from a berthed

ship to trailers, which transfer cargo to yard. Here,

yard cranes pick-up containers from trailers and

stack them in assigned positions. Secondly,

containers stay in the blocks while waiting for their

destination; they are eventually relocated by yard

cranes and trailers in a more proper position.

Thirdly, containers are loaded from blocks to trucks,

and exit from the gate. Similarly, in a railway import

cycle, yard cranes pick-up containers from blocks

and load them on trailers moving from yard to the

railway connection, where special cranes pick-up

containers to put them on departing trains.

In a road/railway export cycle, the sequence goes

in the opposite sense: from terminal gate or railway

connection to blocks and then to vessel ships.

In a transshipment cycle, when a vessel ship

arrives, containers are downloaded to trailers by

quay cranes, transferred to blocks by trailers, picked-

up and stacked by yard cranes. After a consolidation

and/or a delay in their position, containers are

picked-up and transferred to the quay area, where

they are loaded on a feeder ship. The opposite

occurs if a feeder arrives and a vessel departs.

Here, the focus is on the first step of the import

and transshipment cycles. Similar models can be

defined for the following steps and the export cycle.

2.2 Agents in a Container Terminal

The main agents controlling a terminal are:

 the Container Agent (CA): each CA is an

autonomous entity controlling the flow of a

single or a group of containers (stowed in a

ship bay or stacked in yard blocks);

 the Quay crane Agent (QA): it is an

autonomous controller for a (set of) quay

crane(s) with the same performances or the

same reachable ship bays;

 the Trailer Agent (TA): it is associated to a

(set of) trailer(s) with the same performances,

or with the same reachable quay or yard

spaces;

 the Yard crane Agent (YA): it manages a (set

of) yard crane(s) with the same performances,

or associated to the same yard blocks;

 the Railway crane Agent (RA): it controls a

(set of) railway crane(s), to receive containers

from trailers and load them on trains at the

railway connection, or to deliver containers

from trains to trailers;

 the Truck Agent (KA): it follows the

operations executed by a (set of) truck(s),

entering or leaving the terminal by its gate.

In import processes, the CA identifies the most

suitable quay crane to download containers from

ship, then it selects the trailers to transport

containers to their assigned yard blocks, and finally

the yard cranes to pick-up and stack containers in

their assigned block positions. In export processes,

the CA selects the yard cranes to pick-up containers

from blocks, trailers to transport them to the quay

area, and quay cranes to load them into their

assigned bay-row-tier location in the ship.

The decisions taken by a CA are based upon

real-time updated information received from agents

of the alternative available cranes and trailers.

The global control of the activities in the

terminal emerges from the behaviour of concurrently

operating agents. The dynamical interaction between

agents has to be analysed to specify the desired

A DISCRETE-EVENT SYSTEM APPROACH TO MULTI-AGENT DISTRIBUTED CONTROL OF CONTAINER

TERMINALS

301

system behaviour. The precedent observations lead

us to examine interactions between a CA and several

QAs, TAs, and YAs for downloading, transferring,

and stacking containers, or for picking, transferring,

and loading containers. Interactions exist also

between a CA and YAs, TAs, and RAs/KAs when

railway/road cycles are considered.

The agents' decisions are only limited by

constraints of terminal spaces and resources (e.g.,

the limited number of quay cranes that can serve a

fixed ship bay; the limited number of yard cranes),

and of schedules for downloading/loading processes

(establishing the number of containers moved for

each ship bay, the location in the ship hold or cover,

sequence of handling moves, the preferred crane).

Agents' decisions are fulfilled by human

operators devoted to the associated resources (e.g.

crane operators, trailer/truck drivers). The network

of interacting agents may appear and behave as a

unique distributed supervisor for the terminal.

3 DEVS MODELLING OF

AGENTS' DYNAMICS

Each agent in the previously identified classes is

described as an atomic DEVS. Namely, all agents

interact by transmitting outputs and receiving inputs,

which are all considered as event messages. Events

are instantaneous, then timed activities are defined

by a start-event and a stop-event.

For each agent, internal events are triggered by

internal mechanisms, external input events (i.e.

inputs) are determined by exogenous entities (other

agents), and external output events (i.e. outputs) are

generated and directed to other entities.

External or internal events change the agent

state. An agent stays in a state until either it receives

an input or the time specified before an internal

event elapses. In the first case, an external transition

function determines the state next to the received

input; in the second case, an internal transition

function gives the state next to the internal event. An

output function generates the reactions of the agent.

The sequential state, s, refers to the transition

mechanism due to internal events, and is based on

the current value of status (condition between

consecutive events) and other information i peculiar

to the considered agent: s = (status, i). The total state

q = (s, e, DL), where e is the time elapsed since the

last transition, and DL is the decision logic currently

used by the agent to rank and choose the offers

received by other agents.

For a CA, s may include information on: the

current container position; the quay cranes available

for negotiating handling operations; the trailers

available for negotiating transport between quay and

yard; the yard cranes available for negotiating

handling operations from trailer to a block position

or backwards; time scheduled in current state before

the next internal event, if no input occurs.

For QAs, YAs, TAs, RAs, KAs, the sequential

state may include the queued requests coming from

CAs (for availability, for data about offered service,

for confirmation of assigned service, etc.), and the

time prospected before the next internal event.

To summarize, each agent can be represented as

an atomic DEVS in the following way:

A = < X, Y, S,

int

ext

, ta >

(1)

where X is the set of inputs, Y is the set of outputs, S

is the set of sequential states,

int

:S→S is the internal

transition function,

ext

:Q×X→S is the external

transition function, Q={q=(s,e,DL)|s∈S,0≤e≤ta(s)},

:S→Y is the output function, ta:S→ℜ

is the time

advance function, with ℜ

set of positive real

numbers with 0 included.

The negotiation between agents is typically

organized in the following steps. Announcement: an

agent starts a bid and requires availability to other

agents for a service. Offer: the agent requests data

only to the available agents. Data regard the offered

service the queried agents can guarantee. Reward:

the agent selects the best offer between the collected

replies and sends a rewarding message.

Confirmation: the agent waits for a message from

the rewarded agent, then it acquires the service. If

confirmation does not arrive, then the agent selects

another offer in the rank or restarts the bid.

In this paper, the focus is on the interactions

between a CA with QAs, TAs and YAs for

downloading containers from ship to a yard block.

The study can be easily extended to other

negotiations for loading or other processes. Besides,

the status transitions are examined since the status is

the main component of the sequential state.

3.1 Dynamics of Interactions between

Agents in a Downloading Process

To download containers from a ship bay, transport

and stack them into a yard block, each CA interacts

with QAs to choose the quay crane for downloading,

with TAs to select the trailers for moving the

containers from the quay to the yard area, and finally

with YAs to determine the yard cranes for stacking.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

302

We assume that the CA firstly communicates

exclusively with QAs, then with TAs only, finally

with YAs. The negotiation is based on data about the

offered services: a QA gives the estimated time to

wait before the related crane can start downloading

containers, and the estimated time to execute the

task; a TA the estimated times to wait a trailer and

for the transport task; a YA the estimated time for

the yard crane to be ready close to the block, and the

estimated time for the stacking task.

3.1.1 Interactions between a CA and QAs

For t<t

let the CA, say C, associated with a generic

container be in a quiescent status (QUIESC) and let

it begin its activity at t

(input X

). Then C spends

the interval [t

] to send outputs Y

C01

, Y

C02

,…,

C0q

at instants t

, t

,…, t

. These

messages request the availability to all the q

alternative QAs of cranes that can serve the

container. The sequence of requests (REQQAV) is

not interrupted by any internal or external event. C

makes transition at t

(internal event I

In [t

] C waits for answers (WAIQAV) from

QAs. Namely, the request C transmits to each QA

may queue up with similar ones sent by other CAs.

Next transition occurs at t

when either C receives

all the answers from the queried QAs (X

), or a

specified time-out of WAIQAV expires before C

receives all the answers. In case it receives no reply

within the time-out (I

), C returns to REQQAV and

repeats the request procedure. In case of time-out

expiration and some replies received (I

), C

considers only the received answers to proceed. The

repeated lack of valid replies may occur for system

congestion, crane failures, communication faults, or

other unpredictable circumstances. To avoid

indefinite circular waits and improve system fault-

tolerance, we use time-outs and let C repeat the

cycle REQQAV-WAIQAV only a finite number of

times, after which C is replaced by another agent.

If all or some replies arrive before the time-out

expiration, C starts requesting service to the g≤q

available QAs at t

. In [t

] C requests

information with Y

C11

, Y

C12

, …, Y

C1g

at instants

, t

,…, t

. The uninterrupted sequence of

requests in status REQQSE terminates at t

and C

makes transition (I

Then, C spends [t

] waiting for offers from

the available QAs (WAIQOF), as the request C

transmits to each QA may queue up with those sent

by other CAs. Next transition occurs at t

when

either all the answers from the QAs arrive (X

) or a

time-out of WAIQOF expires. In case no reply

comes within the time-out (I

), C returns to

REQQSE and restarts. If time-out expires and some

replies are received (I

), C considers only the

received offers. Again, cycling between REQQSE

and WAIQOF is only for a finite number of times.

Once received the offers from QAs, C uses

] to take a decision for selecting the quay

crane (TAKQDE). At t

the decision algorithm ends

): all the offers are ranked and a QA is selected.

Subsequently, C reserves the chosen crane with

message Y

to the corresponding QA. C takes

] for communicating the choice to the winner

QA (COMCHQ). At t

the communication ends

). Now, the QA sends X

: a rejection, if there is

a conflict with another CA, or a confirmation.

Hence, C uses [t

] to wait for a confirmation

from the selected QA (WAIQCO). The confirmation

is necessary because CAs different from C act

during the decision interval, and the selected crane

can be no longer available. If C receives a rejection

), or no reply within a time-out (I

), it returns

to COMCHQ, sends a new request of confirmation

to the second QA in its rank. If C has no alternative

destinations and the rejection (X

) or the time-out

C10

) occurs, it returns to REQQAV and restarts.

At t

, after receiving a confirmation (X

) from

the selected QA, C makes a transition to DWNLDG:

interval [t

] is for issuing the command Y

the quay crane downloading the container.

Figure 1 depicts the complex dynamics

previously described. Circles represent status-values

and encapsulate outputs, arrows represent internal or

input events.

3.1.2 Other Interactions

When, at time t

, the command is complete (I

C11

), C

starts the negotiation with TAs for a trailer.

C follows the same procedure as with QAs

(requests and waits for availability and then for

offers, decision for the best offering TA, waits for a

confirmation/rejection). Then, the graph in figure 1

continues with a second part (not shown for lack of

space), with the same structure as the first part. This

guarantees modularity, which is important for

simulation and control. After a confirmation, C

issues a transport command, and the container is

loaded on the vehicle associated to the selected TA.

Then, C starts the negotiation with YAs to stack

the container in an assigned block position. Again,

due to the modularity of the approach, the sequence

of status-values follows the same protocol, and,

finally, if a confirmation is received, C issues a

stacking command and gets back to QUIESC.

C stops interacting and remains quiescent until

the beginning of the next negotiation (if any) for

downloading, consolidating or loading another

container. The associated container is downloaded,

transported and stacked in a block where it waits for

the next destination (a block or a ship). If faults

A DISCRETE-EVENT SYSTEM APPROACH TO MULTI-AGENT DISTRIBUTED CONTROL OF CONTAINER

TERMINALS

303

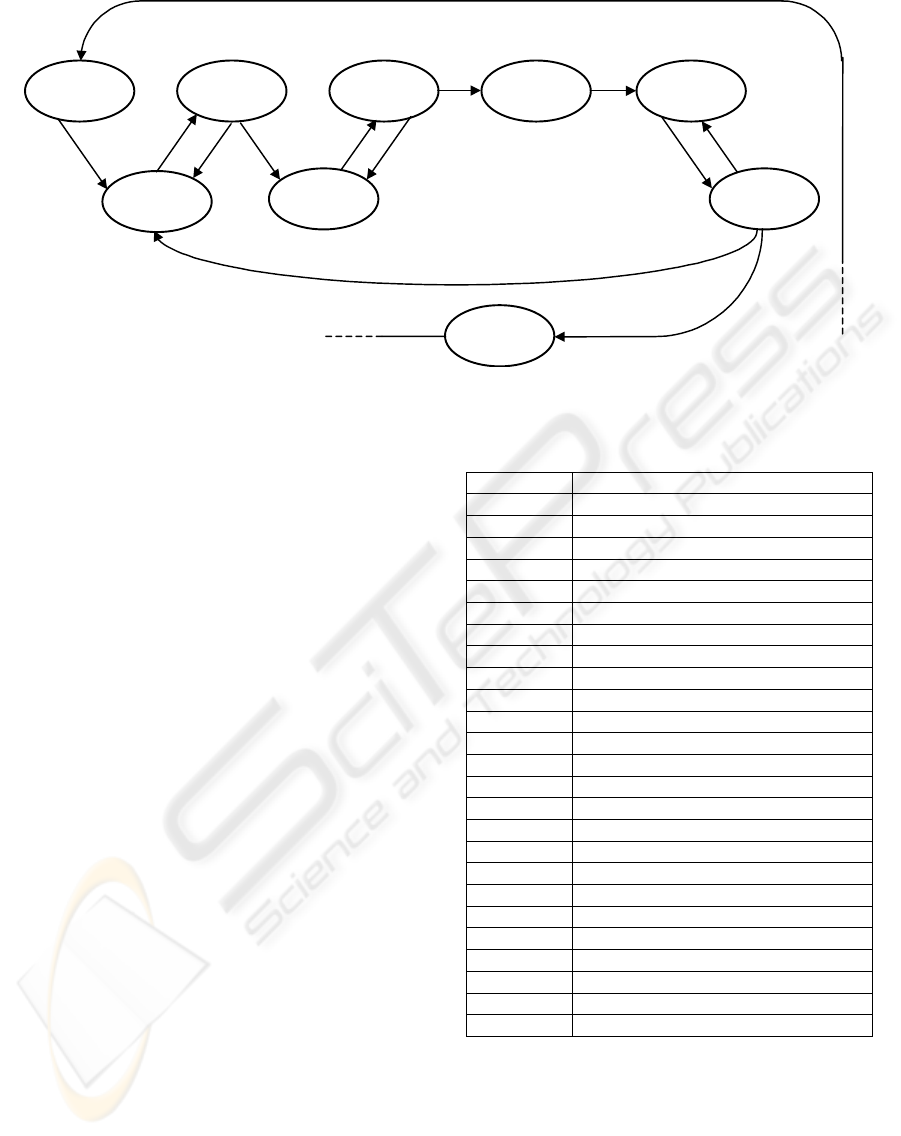
Figure 1: Dynamics of the interaction between a CA when negotiating with QAs.

occur to the selected cranes or trailer, C remains in

QUIESC. Terminal operators restore the normal

operating conditions and the container can be

handled by the selected resources.

3.2 Specification of the DEVS Model of

a Container Agent

We may identify the components of the DEVS

model of a CA, on the basis of the negotiation

mechanism previously described. Table 1 reports the

admissible status-values. Detailed description of

inputs, outputs and internal events is not reported for

lack of space, but it can be easily derived from the

interactions between a CA and QAs, TAs, and YAs.

The sequential state s collects the status-value

and other information i about the CA, which is:

i = ( p, AQ, AT, AY, ta(s) ) (2)

including the current position p of the container (on

ship, picked by quay crane, on trailer, picked by

yard crane, in the yard block); the set AQ of quay

cranes available for the currently negotiated

downloading operations, or the set AT of trailers

available for the currently negotiated transport, or

the set AY of yard cranes available for currently

negotiated stacking tasks; the time ta(s) scheduled in

current state before the next internal event.

The time advance function gives the residual

time ta(s) in state s before the next scheduled

internal invent. E.g., at the time t* of entering a

waiting status, the time-out fixes T

, such that

ta(s) = t*+T

-t, where t is the current time.

Table 1: Status-values for a Container Agent.

Status Activity Description

QUIESC Agent quiescent

REQQAV Request availability to all QAs

WAIQAV Wait for availability from QAs

REQQSE Request service to available QAs

WAIQOF Wait for offers from available QAs

TAKQDE Take decision for the best QA

COMCHQ Communicate choice to selected QA

WAIQCO Wait conf./reject. from selected QA

DWNLDG Command selected QA to download

REQTAV Request availability to all TAs

WAITAV Wait for availability from TAs

REQTSE Request service to available TAs

WAITOF Wait for offers from available TAs

TAKTDE Take decision for the best TA

COMCHT Communicate choice to selected TA

WAITCO Wait conf./reject. from selected TA

TRANSP Command selected TA to transport

REQYAV Request availability to all YAs

WAIYAV Wait for availability from YAs

REQYSE Request service to available YAs

WAIYOF Wait for offers from available YAs

TAKYDE Take decision for the best YA

COMCHY Communicate choice to selected YA

WAIYCO Wait conf./reject. from selected YA

STCKNG Command selected YA to stack

DEVS models can be also specified for the other

agents, and status-transition diagrams can be defined

for the interactions occurring when agents negotiate

tasks in loading or consolidation processes.

QUIESC

WAIQAV WAIQOF TAKQDE

COMCHQ

REQQAV

C01

…Y

C0q

REQQSE

C11

…Y

C1g

WAIQCO

, t

]

, t

]

, t

]

, t

][t

, t

][t

, t

]

, t

]

)

/ I

)

/ I

)

/ I

C10

)

C11

)

, t

]

DWNLDG

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

304

4 IDEAS FOR SIMULATING MAS

The DEVS atomic models can be integrated in a

network, which can be used as a platform for

simulating the MAS controlling a terminal, e.g. the

Taranto Container Terminal (TCT).

In this context, it is possible to simulate not only

the dynamics of terminal activities, the flow of

containers, and the utilization of terminal resources

(cranes, trailers, human operators, etc.), but also the

efficiency of the MAS and its agents (flow of event

messages, status transitions, waiting loops, etc.).

Then, two types of performance indices can be

defined. Namely, it is possible to measure

conventional indices: the total number of (imported,

exported, transshipped) containers; the average

throughput, during downloading (from ship to yard)

or loading (from yard to ship) processes; the average

lateness of containers in the terminal. Moreover, it is

possible to measure the behaviour of the MAS and

the efficiency of the agents' decision policies by

means of: the average number of requests for each

negotiation; the number of loops of status-values

before a final decision is taken by a CA, expressed

in percentile terms with respect to the total number

of operations executed by every CA.

The performance measures can be evaluated both

in steady-state operating conditions and in perturbed

conditions. Perturbations may arise from: hardware

faults or malfunctions; abrupt increase/decrease of

maritime traffic volumes; sudden increase/reduction

of yard space; traffic congestion of trailers;

congestion, delays, message losses, and faults in the

communication between agents.

Then, it is important to measure robustness of

agents' decision laws, to see how they dynamically

react to disturbances and parameter variations, and

eventually to adapt them. The adaptation aims to

make the autonomous agents learn the most

appropriate decision laws in all terminal conditions.

To conclude, the simulation platform will allow

to compare control architectures defined by:

 a static MAS in which CAs use heuristic

decision parameters (estimated time of the

requested task, distance of cranes or trailers);

 a dynamic MAS in which CAs take decisions

by fuzzy weighted combinations of heuristic

decision criteria; the weights can be adapted

by an evolutionary genetic algorithm.

5 CONCLUSIONS

This paper proposes a MAS architecture for

controlling operations in intermodal container

terminal systems. The autonomous agents are

represented as atomic DEVS components. The

interactions between agents are modelled according

to the DEVS formalism to represent negotiations for

tasks when downloading containers from ship to

yard stacking area. The developed model can be

easily extended to describe other processes (loading

containers from yard area to ships, redistributing

containers in the yard area).

The DEVS model of the MAS can be used in a

detailed simulation environment of the TCT, which

allows to measure standard terminal performance

indices and the efficiency of the MAS. Moreover,

open issues are testing and comparing static MAS

and dynamically adapted MAS, if evolutionary

adaptation mechanisms are used.

REFERENCES

Crainic, G., Gendreau, M., Dejax, P., 1993. Dynamic and

stochastic models for the allocation of empty

containers. Oper. Research, Vol. 41, pp. 102-126.

Gambardella, L.M., Rizzoli, A.E., Zaffalon, M., 1998.

Simulation and planning of an intermodal container

terminal. Simulation, Vol. 71, No. 2, pp. 107-116.

Heragu, S.S., Graves, R.J., Kim, B.-I., Onge, A.St., 2002.

Intelligent Agent Based Framework for Manufacturing

Systems Control. IEEE Trans. Sys., Man, and Cyber. -

Part A, Vol. 32, No. 5.

Hsieh, F.-S., 2004. Model and control holonic

manufacturing systems based on fusion of contract

nets and Petri nets. Automatica, 40, pp. 51-57.

Huhns, M.N., Stephens, L.M., 2001. Automating supply

chains. IEEE Int. Comput., Vol. 5, No. 4, pp. 90-93.

Lin, F., Norrie, D.H., 2001. Schema-based conversation

modeling for agent-oriented manufacturing systems.

Computers in Industry, Vol. 46, pp. 259-274.

Logan, B., Theodoropoulos, G., 2001. The distributed

Simulation of Multiagent systems. Proceedings of the

IEEE, Vol. 89, No.2, pp. 174-185.

Shattenberg, B., Uhrmacher, A.M., 2001. Planning Agents

in James. Proc. of the IEEE, Vol. 89, No. 2, pp. 158-

173.

Vis, I.F.A., De Koster, R., 2003. Transshipment of

containers at a container terminal: An overview.

Europ. Jour. of Oper. Research, Vol. 147, pp. 1-16.

Zeigler, B.P., Praehofer, H., Kim, T.G., 2000. Theory of

Modelling and Simulation, Academic Press. New

York, 2

ed..

A DISCRETE-EVENT SYSTEM APPROACH TO MULTI-AGENT DISTRIBUTED CONTROL OF CONTAINER

TERMINALS

305