Direct and Indirect Classification of High-Frequency

LNA Performance using Machine Learning Techniques

Peter C. Hung, Seán F. McLoone, Magdalena Sánchez

Ronan Farrell and Guoyan Zhang

Institute of Microelectronics and Wireless Systems, Department of Electronic Engineering

National University of Ireland Maynooth, Maynooth, Co. Kildare, Ireland

Abstract. The task of determining low noise amplifier (LNA) high-frequency

performance in functional testing is as challenging as designing the circuit itself

due to the difficulties associated with bringing high frequency signals off-chip.

One possible strategy for circumventing these difficulties is to attempt to pre-

dict the high frequency performance measures using measurements taken at

lower, more accessible, frequencies. This paper investigates the effectiveness of

machine learning based classification techniques at predicting the gain of the

amplifier, a key performance parameter, using such an approach. An indirect

artificial neural network (ANN) and direct support vector machine (SVM) clas-

sification strategy are considered. Simulations show promising results with both

methods, with SVMs outperforming ANNs for the more demanding classifica-

tion scenarios.

1 Introduction

In recent years, functional testing of radio frequency integrated circuits (RFIC) has

faced great challenges, especially for multi-gigahertz RF components. Two main

problems exist: relaying the multi-gigahertz RF signal to the external tester without

affecting the performance of tested RF circuits; building RF production testers operat-

ing in the gigahertz range that are not prohibitively expensive. While advances in

technology and market requirements have seen rapid growth in high-frequency and

high integration RFIC designs, testing practice has not followed suit. Indeed, reliable

high-frequency testing has become the dominant factor in the cost and time-to-market

of novel wireless products [1]. Consequently, developing cost-efficient testing solu-

tions is becoming an increasing important research topic [2-4]. Some of the proposed

schemes for RFIC testing are based on an end-to-end strategy in which the output of

the transmitter and the input of the receiver are linked through a loop-back connec-

tion. In this configuration, the testing of the complete system is carried out without

any external stimulus by employing the on-chip digital hardware available. Unfortu-

nately, this solution is not always applicable to all kinds of RF components. Other

recent proposals for RF system testing have focused on the development of method-

ologies and algorithms for automated test, and Design for Testability (DfT). In Built-

C. Hung P., F. McLoone S., Sánchez M., Farrell R. and Zhang G. (2007).

Direct and Indirect Classiﬁcation of High-Frequency LNA Performance using Machine Learning Techniques.

In Proceedings of the 3rd International Workshop on Artiﬁcial Neural Networks and Intelligent Information Processing, pages 66-75

DOI: 10.5220/0001634500660075

 SciTePress

In-Test (BIT), for example, additional circuitry is included that allows high frequency

tests to be performed on-chip and then evaluated using lower frequency or DC exter-

nal testers [3-5]. However, when considering BIT testing, issues such as area over-

head for embedding and BIT power consumption can add significantly to the cost of

design.

In this paper a different approach is considered. Since many RFICs show strong

correlation between their responses to circuit parameter variation at different frequen-

cies, it is hypothesised that knowledge of responses at lower frequencies may provide

sufficient information to allow classification of responses at higher frequencies.

To investigate this hypothesis, testing of a low noise amplifier (LNA), a key com-

ponent in modern telecommunication systems, is used as a case study. A standard 2.4

GHz design, simulated in ADS® using UMC’s 0.18 μm silicon process technology,

provided the data for our experiments [6]. The LNA circuit consisted of 2 bias tran-

sistors (0.18 μm channel length), 4 RF transistors (0.5 μm channel width), 4 resistors,

3 capacitors and 4 inductors and was deemed to be functioning correctly if the value

of S

@ 2.4 GHz was in the range 14.7 dB to 17.2 dB and faulty otherwise. S

, a

critical RF circuit performance measure, is essentially the gain of the amplifier.

Random circuit parameter perturbations representative of typical manufacturing

process variations were generated and the value of S

recorded at different frequen-

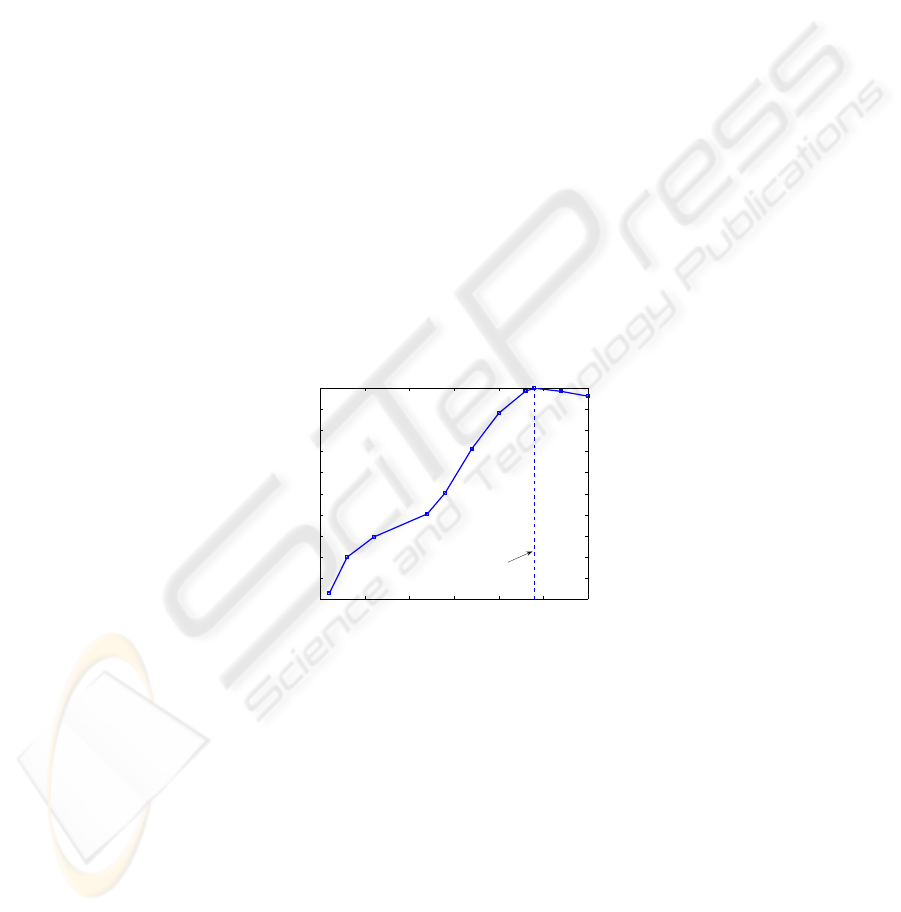
cies. Fig. 1 shows a plot of the correlation that exists between variations in gain (S

@ 2.4 GHz) and variations in the same parameter computed at other frequencies.

There is a strong, but decreasing, correlation evident as the circuit excitation fre-

quency moves away from the operating frequency.

Fig. 1. Correlation coefficients between S

value computed at different frequencies to the

value computed at the target frequency (2.4 GHz).

Even when the correlation is high, circuit performance classification on the basis

of these lower frequencies is not straightforward, as demonstrated in Fig. 2. This

shows the relationship between S

@ 2.4 GHz and the values computed at: (a) 2.0

GHz and (b) 0.1 GHz, respectively, and highlights the fact that even when the corre-

lation is greater than 90% it is not possible to discriminate between the ‘good’ and

‘bad’ circuits effectively. In fact, simple thresholding on the basis of S

@ 2.0 GHz

leads to a misclassification rate of greater than 20%. The misclassification rate in-

creases rapidly as the frequency is reduced and reaches 43.6% for S

@ 0.1 GHz.

0 0.5 1 1.5 2 2.5 3

0.5

0.55

0.6

0.65

0.7

0.75

0.8

0.85

0.9

0.95

Frequency (GHz)

Correlation Coefficient

2.4 GHz

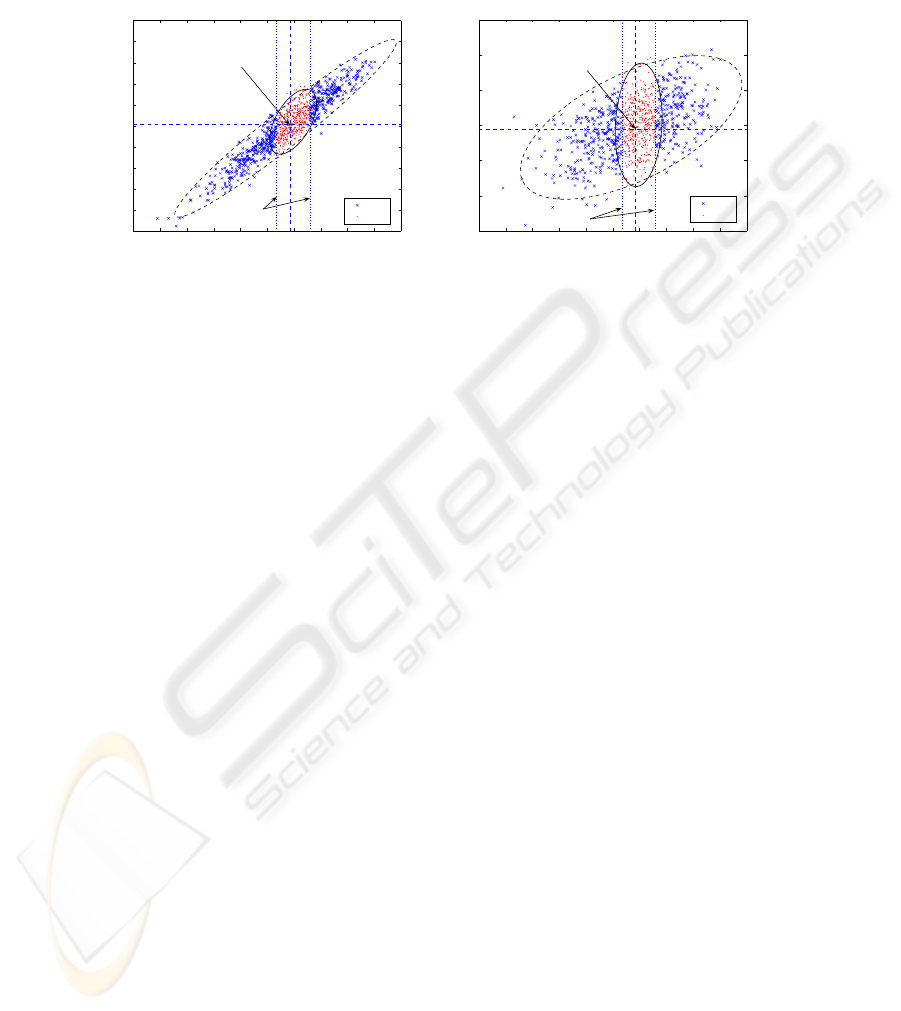
The rapid deterioration in performance is a result of the localised influence of some

parameter variations and the complex nonlinear interaction between circuit compo-

nents.

4 6 8 10 12 14 16 18 20 22 24

S21@2.4 GHz (dB)

S21@2.0 GHz (dB)

samples of bad/good distribution (data corr. coef. = 0.94052)

bad

good

Nomimal

value

Limits of ’good’

samples

4 6 8 10 12 14 16 18 20 22 24

−70

−65

−60

−55

−50

−45

−40

S21@2.4 GHz (dB)

S21@0.1 GHz (dB)

samples of bad/good distribution (data corr. coef. = 0.5136)

bad

good

Limits of ’good’

samples

Nomimal

value

(a) 2.0 GHz (b) 0.1 GHz

Fig. 2. S

parameter relationships for the 2.4 GHz LNA model used in circuit simulations: (a)

@ 2.0 GHz and (b) S

@ 0.1 GHz plotted against S

at the operating frequency.

Since the shape of the frequency response of an LNA is a deterministic nonlinear

function of its component parameters, better classification performance can be ex-

pected if the information from several low frequency measurements can be combined.

To that end, this paper considers the possibility of classifying circuit performance

using machine learning techniques. Two strategies are investigated. In the first, an

Artificial Neural Network (ANN) is trained to predict the value of S

@ 2.4 GHz

from the values measured at other frequencies and then a thresholding rule is applied

to this prediction to perform the circuit classification, while in the second, a Support

Vector Machine (SVM) is trained to directly classify circuit performance on the basis

of the low frequency S

measurements. These two machine learning techniques and

the LNA classification methodology are introduced in Section 2. The simulation

study is then described in Section 3 followed by the results in Section 4. Finally, the

conclusions of the study are presented in Section 5.

2 Machine Learning LNA Performance Classification

Defining the set of N low-frequency S

measurements of the i

LNA circuit as the

feature vector

x (row vector) and the corresponding class label

y , with 1+=

indicating ‘good’ and

1−=

y indicating ‘bad’, we can generate a set of L training

data examples,

LLii

yyy ℜ∈= ),(),,(),,(),(

xxxyX …… ,

(1)

with which to train a classifier to estimate a decision function

}1{:)( ±→ℜ

f x

(2)

that can then be used to classify new LNA circuits. Here, ‘good’ and ‘bad’ are deter-

mined by a threshold function, z

applied to S

@ 2.4 GHz, that is

⎩

⎨

⎧

−

<<+

otherwise1

17.2 14.7 if1

)(

(3)

The decision function in (2) can be estimated directly from the training data by using,

for example, a SVM classifier. Alternatively it can be estimated indirectly by first

predicting the value of S

@ 2.4 GHz from the feature vector,

GHz4.2@)(

Sg →x ,

(4)

and then using a threshold function to perform the classification, that is

}1{))(( :)(

→xx gzf .

(5)

An ANN such as a Multilayer Perceptron can be used to learn the nonlinear mapping

represented by (4).

2.1 Support Vector Machines (SVM)

SVMs, first proposed by Vladimir Vapnik in 1963 [7], are a supervised linear learn-

ing technique widely used for classification problems. They are known to perform

binary classification well in many practical applications. Consider a separating hyper-

plane that divides two classes of data:

ℜ∈ℜ∈=−⋅ bb

,,0 wxw ,

(6)

where w and

b are unknown coefficients, and two additional hyperplanes that are

parallel to the separating hyperplane:

−=−⋅

−

⋅

(7)

Defining the margin as the perpendicular distance between the parallel hyperplanes,

the optimal hyperplane is the one which results in the maximum margin of separation

between the two classes. Mathematically the problem can be expressed as

Liby

,,2,1,1)(tosubject),(min

max …=≥−⋅⋅≡ xwww

(8)

This is a constrained quadratic optimisation problem whose solution

has an ex-

pansion [8]

∑

v xw ,

(9)

where

x are the subset of the training data, referred to as support vectors, located on

the parallel hyperplanes, and

v are the corresponding weighting factors. The linear

SVM (LSVM) decision function is then given by

)()(

SVMLSVM

bzf

−

⋅

xwx

(10)

where

SVM

z is defined as

⎩

⎨

⎧

<−

≥+

0if1

)(

SVM

(11)

The decision function in Eq. (10) can be rewritten as

⎟

⎠

⎞

⎜

⎝

⎛

−⋅=

∑

bvzf

)()(

SVMLSVM

xxx

(12)

with the result that it is only dependent on dot products between the test data vector,

x, and the support vectors. This important property allows SVMs to be extended to

problems where nonlinear partitions of data sets are required. This is achieved by

replacing the dot products by a kernel function

(.)k which meets the Mercer’s condi-

tion [9]:

)()(),(

jiji

k xxxx Φ⋅Φ=

(13)

thereby mapping the data into a higher dimension feature space where linear SVM

classification can be performed. Note the resulting decision function, in the original

data space, will be nonlinear and takes the form

(

)

rzf

SVMSVM

)( =x

, where

∑

−=

bkvr ),(. xx

(14)

In non-separable problems where different classes of data overlap, slack variables

can be introduced so that a certain amount of training error or data residing within the

margin is permitted. This gives rise to a ‘soft margin’ optimisation function [9, 10].

To give users the ability to adjust the amount of training error allowed in the optimi-

sation, a smoothing parameter

is incorporated into the soft margin function, with a

larger

corresponding to assigning a larger penalty to errors.

The Gaussian radial basis function (RBF) defined as

⎟

⎠

⎞

⎜

⎝

⎛

−

−=

RBF

exp),(

(15)

is a popular choice of SVM kernel and the one selected for this application. The pa-

rameter,

, controls the width of the kernel and is determined as part of the classifier

training process.

2.2 Artificial Neural Networks

Neural networks [11] are one of the best known and most commonly-used machine

learning techniques. There are various configurations and structures of NNs, but all

contain an array of neurons that are linked together, usually in multiple layers. In this

application a single hidden layer Multilayer Perceptron (MLP) topology is chosen

because of its universal function approximation capabilities, good generalisation

properties and the availability of robust efficient training algorithms [12].

The output of a single hidden layer MLP can be written as a linear combination of

sigmoid functions (i.e. neurons),

(

)

∑

sigwbg xwx ),(

(16)

where

)exp(1

)(

sig

+⋅+

(17)

Here,

,( Mi ,,2,1 = ) and

b are weights and biases which collectively

form the network weights vector,

w . Defining a Mean Squared Error (MSE) cost

function over the training data

NNNN

)),((

)(

E −=

∑

wxw ,

(18)

with

corresponding to the desired network output for the p

training pattern (i.e.

@ 2.4 GHz), the optimum weights can be determined using gradient based opti-

misation techniques.

3 Simulation Study

To evaluate the potential for employing multiple low frequency S

measurements to

classify LNA S

performance at 2.4 GHz and to compare the performance of the

proposed machine learning classifiers, a Monte Carlo simulation study was under-

taken using a 2.4 GHz LNA model implemented in ADS®. Uniform random varia-

tions were introduced into 38 of the model parameters to represent typical LNA

manufacturing process variations and 10,000 circuit simulations performed. While in

practice circuit parameters might be expected to vary normally around their nominal

values, uniform distributions were chosen to give an even coverage of the LNA pa-

rameter space. Catastrophic failures, such as short-circuits, were not considered as

these can be identified relatively easily using existing IC testing techniques.

For each circuit the S

performance parameter was recorded at 0.1, 0.3, 0.6, 1.2,

1.4, 1.7 and 2.0 GHz and also at the operating frequency (2.4 GHz). This data was

then normalised to have zero mean and unit variance and divided into training and

test data sets, each containing 5,000 samples.

Two different feature vectors were considered in the study, containing S

meas-

urements up to 1.4 GHz and 2.0 GHz, respectively, that is:

]S,S,S,S,S[

4.1

2.1

6.0

3.0

1.0

214.1

(19)

and

]S,S,S,S,S,S,S[

0.2

7.1

4.1

2.1

6.0

3.0

1.0

210.2

=x .

(20)

Here,

S denotes the value of S

at f GHz. In each case the target MLP model out-

put is

4.2

while the target labels for the SVM classifier are given by

)S(

4.2

21th

3.1 MLP Training

MLP training was performed using the hybrid BFGS training algorithm [12] with

stopped minimisation used to prevent over-fitting [13]. The optimum number of neu-

rons (M ) was determined for each model by systematically evaluating different net-

work sizes and selecting the network with the minimum MSE on the test data set.

Training was repeated ten times for each network size to allow for random weight

initialisations and the best set of weights recorded in each case.

The optimum network sizes and resulting model fit, measured in terms of the cor-

relation with the true value of

4.2

S , are summarised in Table 1. For comparison pur-

poses, the correlation between

4.2

S and the measurements at 1.4 and 2.0 GHz are also

given.

Table 1. Optimum MLP classifier model dimensions and resulting model fit.

Feature vector Network dimensions Model fit

4.1

MLP(5,12,1) 0.9364

0.2

MLP(7,15,1) 0.9979

4.1

- 0.7537

0.2

- 0.9408

As expected, the exploitation of multiple frequencies results in much better pre-

dictability of

4.2

S than using the measurement at a single frequency. Notably, the

information provided by

0.2

S is still marginally greater than the combined information

provided by all measurements up to 1.4 GHz. The classification performance of these

networks, when employed in the indirect LNA classifier scheme, will be reported in

Section 4.

3.2 SVM Training

SVM training was performed using the Matlab® package simpleSVM [14]. The ker-

nel width parameter

and smoothing parameter C were fine tuned manually and

optimised on the basis of classification performance on the test data set. The final

values selected were

9.0=

and 000,100

C .

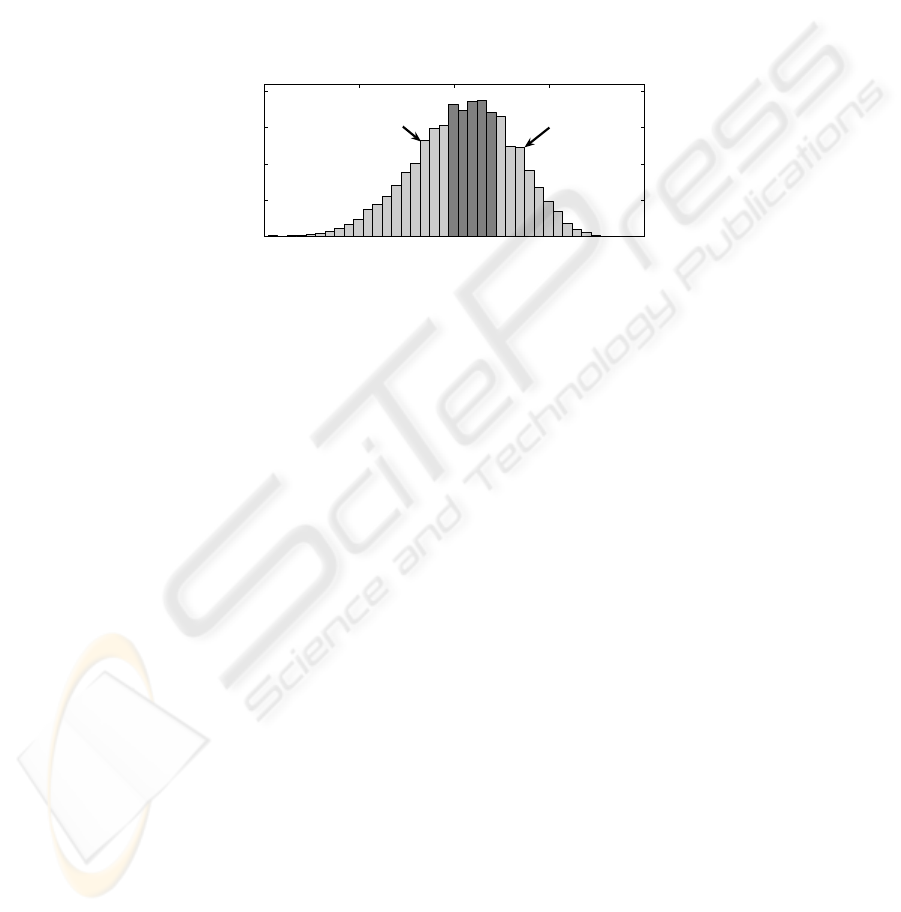
Initial SVM results were quite poor despite expectations of superior performance

to indirect classification using MLPs (results presented in Section 4). It was deter-

mined that this was due to the bimodal distribution of the out-of-specification circuits

forming the ‘bad’ class, i.e. it consists of two segments separated by the ‘good’ class,

as shown in Fig. 3.

5 10 15 20 25

200

400

600

800

@ 2.4 GHz (dB)

Historgram Frequency

Good

Bad lower

Bad upper

Fig. 3. Histogram of ‘good’ and ‘bad’ circuits as defined by the S

performance criteria.

The a priori knowledge of the distribution of the ‘bad’ circuits can be taken into

account by splitting the ‘bad’ samples into ‘bad lower’ and ‘bad upper’ samples,

thereby introducing 3 classes – ‘bad lower’, ‘good’ and ‘bad upper’. SVM classifica-

tion is then performed in two-stages. Firstly, two binary SVMs are trained, one to

classify LNAs as either ‘bad lower’ or ‘not bad lower’, and one to classify LNAs as

either ‘bad upper’ or ‘not bad upper’. Then the overall classification is obtained from

a weighted linear combination of the individual decision functions, that is:

)(

BUBLSVMSVM3

rKrzf

(21)

Here,

is as defined in Eq. (14), subscripts BL and BU represent the ‘bad lower’ and

‘bad upper’ classifiers and the constant

is a scalar which is chosen to maximise

the correlation between

SVM3

f and the true class labels over the training data.

This 3-class SVM approach is denoted SVM3 while the original two class SVM

classifier will be referred to as SVM2.

4 Results

The performance of the MLP, SVM2 and SVM3 LNA classifiers was measured in

terms of the following metrics computed on the test data set:

GPR: good pass rate - Percentage of good LNAs passed;

BFR: bad fail rate - Percentage of bad LNAs failed;

FR: failure rate - Percentage of passed LNAs incorrectly classified as ‘good’;

MCR: misclassification rate - Percentage of LNAs incorrectly classified.

Since the good pass rate (GPR) and bad fail rate (BFR) of a classifier vary as a func-

tion the classification threshold, with one increasing as the other deceases, the thresh-

old can be adjusted to control one or other of these metrics. Here, the threshold of

each classifier was adjusted to give a fixed BFR, reflecting the importance in the

electronics industry of controlling the number of faulty components released to the

market.

Table 2 shows the mean performance of each classifier when their thresholds were

selected to give a BFR of 90% and 75%, respectively. The result for classification on

the basis of single frequency measurements at 1.4 and 2.0 GHz are also included for

comparison. To provide robust estimates, the metrics were computed by averaging

over 100 batches of LNAs generated from the test data set using sampling with re-

placement. Each batch consisted of 500 ‘good’ and 500 ‘bad’ circuits randomly se-

lected (with replacement) from a total of 1,795 ‘good’ and 3,205 ‘bad’ examples in

the data set.

Table 2. Mean performance of the MLP, SVM2 and SVM3 LNA classifiers.

BFR (%)

90 75

Inputs

Method

GPR

(%)

MCR

(%)

GPR

(%)

MCR

(%)

MLP 57.11 14.88 26.45 81.03 23.55 21.99

1.4

SVM2 44.18 18.43 27.96 77.32 24.41 11.39

SVM3

82.30

10.82 13.85

90.85

21.56 17.08

MLP

99.70

9.09 5.15

100.00

19.97 12.50

2.0

SVM2 84.40 10.57 12.80 97.33 20.41 13.83

SVM3 97.60 9.28 6.20 99.34 20.09 12.83

4.1

- 19.98 33.29 45.01 47.13 34.63 38.94

0.2

- 55.48 15.24 27.27 84.65 22.78 20.17

Comparing the different classifiers, it can be seen that SVM3 provides the most

consistent performance. Although the MLP classifier produces the best results when

using frequencies up to 2.0 GHz, SVM3 is only around 2% and 0.7% behind. More

importantly, when LNA classification is performed using S

measurements up to 1.4

GHz only, SVM3 outperforms the MLP solution by 25% and 9% respectively. It is

noted that high GPRs are always accompanied by correspondingly low values of FR

and MCR. As expected, the performance of all classifiers deteriorates when only the

lower frequency S

measurements (x

1.4

) are considered, though SVM3 and MLP still

outperform the classifications obtained using a single S

measurement at 2.0 GHz.

Interestingly, the SVM classifier was only able to outperform the MLP classifier

when the a priori knowledge of the bimodal distribution of the out-of-specification

LNAs was taken into account. In all cases SVM2 is substantially inferior to both the

MLP and SVM3 classifiers. This suggests that while SVMs are the natural setting for

classification they do not always yield the optimum results.

Although this study does not consider catastrophic IC failures, they can be identi-

fied relatively easily using other simple tests such as supply current tests. Overall, the

results successfully demonstrate the usefulness of machine learning techniques for

LNA functional testing. For example, it can lower the cost of testing by extending

the frequency range of existing ATE testers by as much as 70%.

5 Conclusions

Functional testing of high-frequency LNAs is becoming a prohibitively expensive

and time-consuming exercise, due to the difficulties with bringing such signals off-

chip. This paper proposes a novel testing strategy in which machine learning classifi-

ers are used to predict high-frequency LNA performance by combining information

from several lower frequency measurements. Promising results are obtained using

both direct SVM and indirect MLP classifiers.

Acknowledgements

The authors gratefully acknowledge the financial support of Enterprise Ireland.

References

1. Ferrario, J., Wolf, R., Ding, H.: Moving from mixed signal to RF test hardware develop-

ment. IEEE Int. Test Conference (2001) 948–956

2. Lau, W. Y.: Measurement challenges for on-wafer RF-SOC test. 27th Annual IEEE/SEMI

Int. Elect. Manufact. Tech. Symp. (2002) 353–359

3. Negreiros, M., Carro, L., Susin, A.: Low cost on-line testing of RF circuits. 10th IEEE Int.

On-Line Testing Symp. (2004) 73–78

4. Doskocil, D. C.: Advanced RF built in test. AUTOTESTCON '92 IEEE Sys. Readiness

Tech. Conf. (1992) 213–217

5. Goff, M. E., Barratt, C. A.: DC to 40 GHz MMIC power sensor. Gallium Arsenide IC

Symp. (1990) 105–108.

6. Allen, P. E., Holberg, D. R.: CMOS analog circuit design. 2nd edn. Oxford University

Press, Oxford (2002)

7. Vapnil V., Lerner A.: Pattern recognition using generalised portrait method. Automation

and Remote Control 24 (1963)

8. Hearst, M.A.: SVMs – a practical consequence of learning theory. IEEE Intelligent Sys.

(1998) 18–21

9. Burges, C. J.: A tutorial on support vector machines for pattern recognition. Data Mining

and Knowledge Discovery 2 (1998) 121–167

10. Cortes C., Vapnik V.: Support vector networks. Machine Learning 20 (1995) 273–297

11. Haykin, S.: Neural Networks: A comprehensive foundation. 2nd edn. Prentice Hall, New

Jersey (1998)

12. McLoone S., Brown M., Irwin G., Lightbody G.: A hybrid linear/nonlinear training algo-

rithm for feedforward neural networks. IEEE Trans. on Neural Networks 9 (1998) 669-684

13. Sjöberg, J., Ljung, L.: Overtraining, regularization, and searching for minimum with appli-

cation to neural networks. Int. J. Control 62 (1995) 1391-1407

14. Vishwanathan S. V. N., Smola A. J., Murty M. N.: SimpleSVM. Proc. 20th Int. Conf.

Machine Learning (2003)