Cooperative Collision Avoidance between Multiple

Robots based on Bernstein-B

ezier Curves

Igor

Skrjanc and Gregor Klan

car

Faculty of Electrical Engineering, University of Ljubljana

ska 25, SI-1000 Ljubljana, Slovenia

Abstract. In this paper a new cooperative collision-avoidance method for mul-

tiple nonholonomic robots based on Bernstein- B

ezier curves is presented. The

reference path of each robot from the start pose to the goal pose, is obtained

by minimizing the penalty function, which takes into account the sum of all the

paths subjected to the distances between the robots, which should be bigger than

the minimal distance deﬁned as the safety distance. When the reference paths

are deﬁned the model predictive trajectory tracking is used to deﬁne the control.

A prediction model derived from linearized tracking-error dynamics is used to

predict future system behavior. A control law is derived from a quadratic cost

function consisting of the system tracking error and the control effort. The results

of the simulation and some future work ideas are discussed.

1 Introduction

Collision avoidance is one of the main issues in applications for a wide variety of tasks

in industry, human-supported activities, and elsewhere. Often, the required tasks cannot

be carried out by a single robot, and in such a case multiple robots are used coop-

eratively. The use of multiple robots may lead to a collision if they are not properly

navigated. Collision-avoidance techniques tend to be based on speed adaptation, route

deviation by one vehicle only, route deviation by both vehicles, or a combined speed

and route adjustment. When searching for the best solution that will prevent a collision

many different criteria are considered: time delay, total travel time, planned arrival time,

etc. Our optimality criterion will be the minimal travel time, which directly implies a

minimal total length of the robot paths, subject to a minimal safety distance between all

the robots.

In the literature many different techniques for collision avoidance have been pro-

posed. The ﬁrst approaches proposed avoidance, when a collision between robots is

predicted, by stopping the robots for a ﬁxed period or by changing their directions.

The combination of these techniques is proposed in [1]. The behavior-based motion

planning of multiple mobile robots in a narrow passage is presented in [2]. Intelligent

learning techniques were incorporated into neural and fuzzy control for mobile-robot

navigation to avoid a collision as proposed in [3].

In our paper the control of multiple mobile robots to avoid collisions in a two-

dimensional free-space environment is separated into the path planning for each indi-

vidual robot to reach its goal pose as fast as possible. The second part of the task is to

design the control that will ensure the perfect trajectory tracking of the mobile robots.

Skrjanc I. and Klan

car G. (2007).

Cooperative Collision Avoidance between Multiple Robots based on Bernstein-B

ezier Curves.

In Proceedings of the 3rd International Workshop on Multi-Agent Robotic Systems, pages 34-43

 SciTePress

Several controllers were proposed for mobile robots with nonholonomic constraints.

An extensive review of nonholonomic control problems can be found in [4]. In trajectory-

tracking control a reference trajectory is usually obtained by using a reference robot;

therefore, all kinematics constraints are implicitly considered by a reference trajectory.

From the reference trajectory a feed-forward system of inputs combined with a feed-

back control law are mostly used [5]. Lyapunov stable time-varying state-tracking con-

trol laws were pioneered by [9]. The stabilization to the reference trajectory requires

a nonzero motion condition. Many variations and improvements to this state-tracking

controller followed in subsequent research [10]. A tracking controller obtained with

input-output linearization is used in [5], a saturation feedback controller is proposed in

[11] and a dynamic feedback linearization technique is used in [6].

The paper is organized as follows. In Section 2 the problem is stated. The concept

of path planning is shown in Section 3. The idea of optimal collision avoidance for

multiple mobile robots based on B

ezier curves is discussed in Section 4. The trajectory-

tracking controller design where the control strategy consists of feed-forward and feed-

back actions is introduced in Section 5. In Section 5.1 the proposed model predictive

controller is derived. The simulation results of the obtained collision-avoidance control

are presented in Section 6 and the conclusion is given in Section 7.

2 Statement of the Problem

The collision-avoidance control problem of multiple nonholonomic mobile robots is

proposed in a two-dimensional free-space environment. The simulations are performed

for a small two-wheel differentially driven mobile robot of dimension 7.5 × 7.5 × 7.5

cm. The architecture of our robots has a nonintegrable constraint in the form ˙x sin θ −

˙y cos θ = 0 resulting from the assumption that the robot cannot slip in a lateral direction

where q(t) = [x(t) y(t) θ(t)]

are the generalized coordinates The kinematics model

of the mobile robot is

˙q (t) =





cos θ(t) 0

sin θ(t) 0

0 1







v(t)

ω(t)



(1)

where v(t) and ω(t) are the tangential and angular velocities of the platform. During

low-level control the robot’s velocities and accelerations are bounded within the maxi-

mal allowed velocities and accelerations, which prevents the robot from slipping.

The danger of a collision between multiple robots is avoided by determining the

strategy of the robots’ navigation, where we deﬁne the reference path to fulﬁl certain

criteria. The reference path of each robot from the start pose to the goal pose is obtained

by minimizing the penalty function, which takes into account the sum of all the paths

subjected to the distances between the robots, which should be larger than the deﬁned

safety distance. When the reference paths are deﬁned the model predictive trajectory

tracking is used to deﬁne the control.

3 Path Planning based on Bernstein-B

ezier Curves

Given a set of control points P

, P

, . . . , P

, the corresponding Bernstein-B

ezier curve

(or B

ezier curve) is given by

r(λ) =

i=0

i,b

(λ)p

where B

i,b

(λ) is a Bernstein polynomial, λ is a normalized time variable (λ = t/T

max

0 ≤ λ ≤ 1) and p

, 0 = 1, . . . , b stands for the local vectors of the control point P

= P

+ P

, where P



, P



is the control point with coordinates P

and P

, and e

and e

are the corresponding base unity vectors). The Bernstein-B

ezier

polynomials, which are the base functions in the B

ezier-curve expansion, are given as

follows:

i,b

(λ) =





(1 − λ)

b−i

, i = 0, 1, . . . , b

which have the following properties: 0 ≤ B

i,b

(λ) ≤ 1, 0 ≤ (λ) ≤ 1 and

i=0

i,b

The B

ezier curve always passes through the ﬁrst and last control point and lies

within the convex hull of the control points. The curve is tangent to the vector of the

difference p

− p

at the start point and to the vector of the difference p

− p

b−1

at the

goal point. A desirable property of these curves is that the curve can be translated and

rotated by performing these operations on the control points. The undesirable properties

of B

ezier curves are their numerical instability for large numbers of control points, and

the fact that moving a single control point changes the global shape of the curve. The

former is sometimes avoided by smoothly patching together low-order B

ezier curves.

The properties of B

ezier curves are used in path planning for nonholonomic mobile

robots. In particular, the fact of the tangentiality at the start and at the goal points and

the fact that moving a single control point changes the global shape of the curve. Let us

assume the starting pose of the mobile robot is deﬁned in the generalized coordinates

as q

= [x

, y

, θ

]

and the goal pose is deﬁned as q

= [x

, y

, θ

]

, which means

that the robot starts in position P

, y

) with orientation θ

and has a goal deﬁned

with position P

, y

) with orientation θ

. The property of tangentiality requires the

deﬁnition of the neighboring points P

, y

) and P

, y

), which become

+ d cos θ

, y

+ d sin θ

), P

+ d cos (θ

+ π), y

+ d sin (θ

+ π)) (2)

where d stands for the distance between P

and P

and between P

and P

. The distance

d is usually deﬁned relatively to the distance between the start and the goal point D

(D =| p

− p

|) deﬁned as d = γD, 0 < γ < 0.5. These four control points P

, P

and P

uniformly deﬁne the third order B

ezier curve. The need for ﬂexibility

of the global shape and the fact that moving a single control point changes the global

shape of the curve imply the introduction of another point, which will be denoted as

, y

). By changing the position of point P

the global shape of the curve changes.

This means that having in mind the ﬂexibility of the global shape of the curve and the

start and the goal pose of the mobile robot, the path can be planned by four ﬁxed points

and one variable point. The B

ezier curve is now deﬁned as a sequence of points P

, P

and P

in Fig 1. This means that we are dealing with Bernstein polynomials of

the fourth order (B

i,b

, i = 0, . . . , b, b = 4). The curve is deﬁned as follows:

r(λ) = B

0,4

+ B

1,4

+ B

2,4

+ B

3,4

+ B

4,4

(3)

P xy

1 1 1

( , )

P x y

s s s

( , )

P xy

o o o

( , )

P xy

2 2 2

( , )

P xy

g g g

( , )

Fig.1. The B

ezier curve.

4 Optimal Collision Avoidance based on Bernstein-B

ezier Curves

In this subsection a detailed presentation of cooperative multiple robots collision avoid-

ance based on B

ezier curves will be given. Let as assume the number of robots equals

n. The i-th robot is denoted as R

and has the start position deﬁned as P

, y

)

and the goal position deﬁned as P

g i

, y

g i

). The reference path of i-th robot will be

denoted with the B

ezier curve r

(λ) = [x

(λ), y

(λ)]

. By choosing maximal time of

the experiment T

max

(t = T

max

λ, 0 ≤ λ ≤ 1) the robots tangential velocity proﬁles

are determined. T

max

is determined by the fastest robot R

as T

max

(λ))

max

i = 1, . . . , n, 0 ≤ λ ≤ 1, where v

max

is maximal allowed tangential robot velocity.

Maximal time T

max

is then common to all robots R

. In Fig. 2 a collision avoidance for

n = 2 is presented for reasons of simplicity.

The safety margin to avoid a collision between two robots is, in this case, deﬁned

as the minimal necessary distance between these two robots. The distance between the

robot R

and R

is r

(λ) =| r

(λ) − r

(λ) |, i = 1, . . . , n, j = 1, . . . , n, i 6= j.

Deﬁning the minimal necessary safety distance as d

, the following condition for

collision avoidance is obtained r

≥ d

, 0 ≤ λ ≤ 1, i, j. Fulﬁlling this criteria means

that the robots will never meet in the same region deﬁned by a circle with radius d

which is called a non-overlapping criterion. At the same time we would like to minimize

the length of the path for each robot, which is deﬁned as s

. The length s

(λ) is deﬁned

as s

(λ) =

(λ)dλ, where v

(λ) stands for the tangential velocity in the normalized

P xy

g g g1 1 1

( , )

P x y

s s s1 1 1

( , )

P x y

s s s2 2 2

( , )

P xy

g g g2 2 2

( , )

( )lr

1 2

-r r

Fig.2. Collision avoidance based on Bernstein-B

ezier.

variable λ and the length of the path of the robot R

from the start control point to the

goal point is now calculated as:

(λ) =|

r(λ) |=



˙x

(λ) + ˙y

(λ)



, s



( ˙x

(λ)) + ˙y

(λ))



dλ

where ˙x

(λ) stands for

(λ)

dλ

and ˙y

(λ) for

(λ)

dλ

. Assuming that the start and goal

control points are known, the global shape and length of each path can be optimized by

changing the ﬂexible control point P

. The collision-avoidance problem is now deﬁned

as an optimization problem as follows:

minimize

i=1

subject to d

− r

(λ) ≤ 0, ∀i, j, i 6= j, 0 ≤ λ ≤ 1 (4)

The minimization problem is called an inequality optimization problem and can be

introduced as the minimization of the following penalty function

F (P

) =

+ c

, Γ

1, min r

(λ) < d

0, min r

(λ) > d

, i, j, i 6= j, 0 ≤ λ ≤ 1 (5)

where c stands for a large scalar to penalize the unfulﬁllment of constraints. The

solution of the minimization problem min

F is a set of n control points P

, . . . , P

}. Each optimal control point P

, i = 1, . . . , n uniformly deﬁnes one

optimal path, which ensures collision avoidance in the sense of a safety distance and

will be used as a reference trajectory of the ith robot and will be denoted as r

(λ).

To deﬁne the feasible reference path that will be collision safe, the real time should

be introduced. In the real system the tangential and the angular velocities are limited to

max

, ω

max

). Using the relation v(t) =

v(λ)

max

the maximal time T

max

can be deﬁned

to fulﬁl the velocity limitation (T

max

≥

max v(λ)

max

5 Path Tracking

The previously obtained optimal collision-avoidance path for the ith robot is deﬁned as

(t) = [x

(t), y

(t)]

, i = 1, . . . , n. In this section the development of a predictive

path-tracking controller will be presented. The path-tracking control is realized as a sum

of the feed-forward and feed-back controls. The feed-forward control for the ith robot

is calculated from a feasible reference path r

(t) = [x

(t), y

(t)]

, which enables us

to reach a desired pose. The feed-forward control inputs v

(t) and ω

(t) are derived

using a kinematic model (1). The tangential velocity v

(t) and the tangent angle of

each point on the path are calculated as follows

(t) =



˙x

(t) + ˙y

(t)



, ω

(t) =

˙x

(t)¨y

(t) − ˙y

(t)¨x

(t)

˙x

(t) + ˙y

(t)

= v

(t)κ(t)

(6)

where κ(t) is the path curvature. The necessary condition in the path-design procedure

is a twice-differentiable path and a nonzero tangential velocity v

(t) 6=0.

If for some time t the tangential velocity is v

(t)=0, the robot rotates at a ﬁxed

point with the angular velocity ω

(t) calculated from an explicitly given θ

(t).

The feedback control law is derived from a linear time-varying system obtained by

an approximate linearization around the trajectory. The obtained linearization is shown

to be controllable as long as the trajectory does not come to a stop, which implies that

the system can be asymptotically stabilized by smooth time-varying linear or nonlinear

feedback. The tracking error e(t) = [e

(t) e

(t)]

of a mobile robot expressed in

the frame of the real robot reads

e =





cos θ sin θ 0

− sin θ cos θ 0

0 0 1





− q) . (7)

Considering the robot kinematics (1) and derivating relations (7) the following kine-

matics model is obtained

e =





cos e

sin e

0 1













−1 e

0 −e

0 −1





u (8)

where u = [v ω]

is the velocity input vector and v

and ω

are already deﬁned in (6).

The robot input vector u is further deﬁned as the sum of the feed-forward and feedback

control actions (u = u

+ u

) where the feed-forward input vector, u

, is obtained

by a nonlinear transformation of the reference inputs u

= [v

cos e

]

and the

feedback input vector, is u

= [u

]

, which is the output of the controller deﬁned

in section 5.1.

Using the relation u = u

+ u

, rewriting (8) and furthermore, by linearizing the

error dynamics around the reference trajectory (e

= e

= 0, u

= u

= 0)

the following linear model is obtained

e =





0 ω

−ω

0 v

0 0 0





e +





−1 0

0 0

0 −1





(9)

which in the state-space form is

e = A

e + B

. According to Brockett’s condition

[12] a smooth stabilization of the system (1) or its linearization is only possible with

time-varying feedback. In the following the obtained linear model is used in the derived

predictive control law.

5.1 Model Predictive Control based on a Robot Tracking-error Model

To design the controller for trajectory tracking the system (9) will be written in discrete-

time form as

e(k + 1) = Ae(k) + Bu

(k)

where A ∈ R

× R

, n is the number of state variables and B ∈ R

× R

, m is the

number of input variables. The discrete matrix A and B can obtained as follows:A =

I + A

, B = B

which is a good approximation during a short sampling time

The idea of the moving-horizon control concept is to ﬁnd the control-variable values

that minimize the receding-horizon quadratic cost function (in a certain interval denoted

with h) based on the predicted robot-following error:

J(u

, k) =

i=1

(k, i)Qǫ(k, i) + u

(k, i)Ru

(k, i) (10)

where ǫ(k, i) = e

(k + i) − e(k + i|k) and e

(k + i) and e(k + i|k) stands for the

reference robot following-trajectory and the robot-following error, respectively, and Q

and R stand for the weighting matrices where Q ∈ R

× R

and R ∈ R

× R

, with

Q ≥ 0 and R ≥ 0.

Output prediction in the discrete-time framework In the moving time frame the

model output prediction at the time instant h can be written as:

e(k + h|k) = Π

h−1

j=1

A(k + j|k)e(k) +

i=1



h−1

j=i

A(k + j|k)



B(k + i − 1|k)·

·u

(k + i − 1) + +B(k + h − 1|k)u

(k + h − 1) .

(11)

Deﬁning the robot-tracking prediction-error vector

∗

(k) =



e(k + 1|k)

e(k + 2|k)

. . . e(k + h|k)



where E

∗

∈ R

n·h

for the whole interval of observation (h) and the control vector

(k) =



(k) u

(k + 1) . . . u

(k + h − 1)



and

Λ(k, i) = Π

h−1

j=i

A(k + j|k)

the robot-tracking prediction-error vector is written in the form

∗

(k) = F(k)e(k) + G(k)U

(k) (12)

where

F(k) = [A(k|k) A(k + 1|k)A(k|k) . . . Λ

Λ(k, 0)]

, (13)

and G(k) = [g

] , i = 1, ..., n, j = 1, ..., b, b = max(h, n), g

= B(k |k),g

A(k+1|k)B(k|k), g

= B(k+1|k), g

= Λ

Λ(k, 1)B(k|k), g

= Λ

Λ(k, 2)B(k+1|k),

= B(k + h − 1|k). and F(k) ∈ R

n·h

× R

, G(k) ∈ R

n·h

× R

m·h

The objective of the control law is to drive the predicted robot trajectory as close

as possible to the future reference trajectory, i.e., to track the reference trajectory. This

implies that the future reference signal needs to be known. Let us deﬁne the reference

error-tracking trajectory in state-space as e

(k + i) = A

e(k). for i = 1, . . . , h. This

means that the future control error should decrease according to dynamics deﬁned with

the reference model matrix A

. Deﬁning the robot reference-tracking error vector

∗

(k) =



(k + 1)

(k + 2)

. . . e

(k + h)



, E

∗

∈ R

n·h

for the whole interval of observation (h) the following is obtained

∗

(k) = F

e(k), F



. . . A



, F

∈ R

n·h

× R

. (14)

Control law The idea of MPC is to minimize the difference between the predicted

robot-trajectory error and the reference robot-trajectory error in a certain predicted in-

terval.

The cost function is, according to the above notation, now written as

J(U

) = (E

∗

− E

∗

)

Q (E

∗

− E

∗

) + U

. (15)

The control law is obtained by the minimization (

∂J

∂U

= 0) of the cost function and

becomes

(k) =



QG + R



−1

Q (F

− F) e(k) (16)

where

Q = diag(Q) and R = diag(R). This means that Q ∈ R

n·h

× R

n·h

and

R ∈ R

m·h

× R

m·h

Let us deﬁne the ﬁrst m rows of the matrix



QG + R



−1

Q (F

− F) ∈

m·h

× R

as K

mpc

. Now the feedback control law of the model predictive control is

given by

(k) = K

mpc

· e(k), K

mpc

∈ R

× R

(17)

6 Simulation Results

In this section the simulation results of the optimal cooperative collision avoidance

between three mobile robots are shown. The study was made to elaborate the possible

use in the case of a real mobile-robot platform. In the real platform we are faced with

the limitation of control velocities and accelerations. The maximal allowed tangential

velocity and angular velocity were v

max

= 0.5 m/s and ω

max

= 13 rad/s, while the

maximal allowed tangential wheel acceleration is a

max

= 3m/s

. Because of relatively

hight maximal angular velocity and tangential wheel acceleration only the tangential

velocity was taken into account to deﬁne the maximal time between the start position

of the robots and the goal position, which is deﬁned as T

max

≥

max v(λ)

max

2.1m

0.5ms

−1

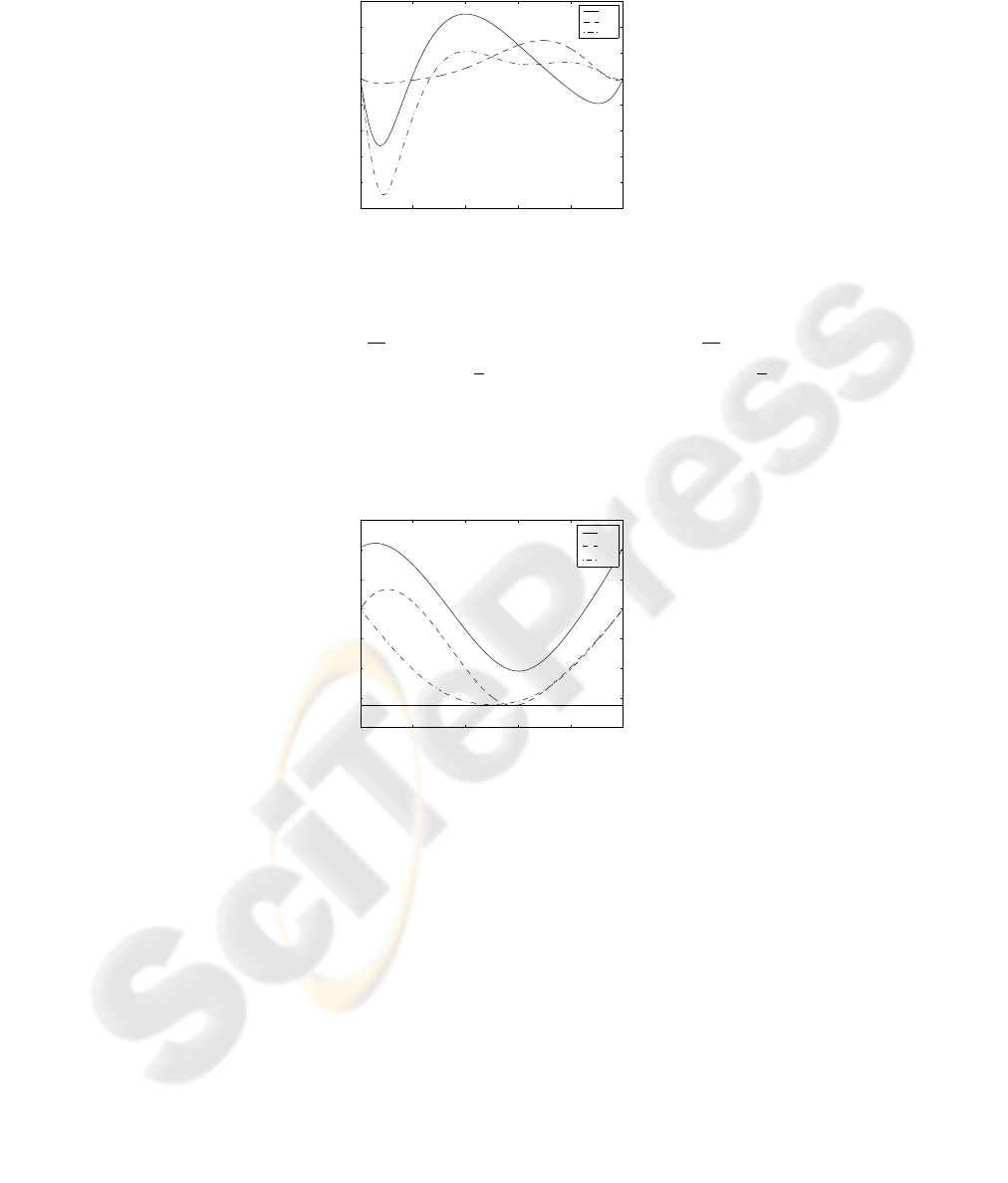
4.02s where the maximal normalized tangential velocity max

(λ) = 2.1m is deﬁned

from Fig. 3. The starting pose of the ﬁrst mobile robot R

in generalized coordinates is

deﬁned as q



0, 1,



and the goal pose as q

g 1



1, 0, −



. The second robot

0 0.2 0.4 0.6 0.8 1

0.6

0.8

1.2

1.4

1.6

1.8

2.2

, v

Fig.3. The velocities of avoiding robots R

, R

and R

in normalized time variable.

starts in q



1, 0, −

3π



and has the goal pose q

g 2



0, 1,

3π



. The third

robot R

has the start pose q



0, 0, −



and the goal pose q

g 3



1, 1,



. The

x and y coordinates are deﬁned in meters. The safety distance is deﬁned as d

= 0.35m.

The parameter d, which is used to deﬁne the control points P

and P

, equals 0.4m

(min

= 1m, γ = 0.4). In Fig. 4 the distances between the mobile robots are

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

1.2

1.4

1.6

, r

Fig.4. The distances between avoiding robots R

, R

and R

shown. It is also shown that all the distances r

, r

and r

satisfy the safety-distance

condition. They are always bigger than prescribed safety distance d

7 Conclusion

The optimal cooperative collision-avoidance approach based on B

ezier curves allows

us to include different criteria in the penalty functions. In our case the reference path of

each robot from the start pose to the goal pose is obtained by minimizing the penalty

function, which takes into account the sum of all the paths subjected to the distances

between the robots, which should be bigger than the minimal distance deﬁned as the

safety distance. Current approach as presented does not include explicit velocity and

acceleration constraints to be imposed to each robot, this remaining the future research

work.

References

1. R.C. Arkin, Cooperation without communication: multiagent schema-based robot naviga-

tion, J Robot Syst., 1992, 9, 351–364,

2. L. Shan and T. Hasegawa, Space reasoning from action observation for motion planning of

multiple robots: mutal collision avoidance in a narrow passage, J Robot Soc Japan, 1996, 14,

1003–1009.

3. C.G. Kim and M.M.Triverdi, A neuro-fuzzy controller for mobile robot navigation and mul-

tirobot convoying, IEEE Trans Sys Man Cybernet SMC Part-B, 1998, 28, 829–840.

4. I. Kolmanovsky and N. H. McClamroch, Developments in Nonholonomic Control Problems,

IEEE Control Systems, 1995, 15, 6, 20–36.

5. N. Sarkar, X. Yun and V. Kumar, Control of mechanical systems with rolling constraints: Ap-

plication to dynamic control of mobile robot, The International Journal of Robotic Research,

1994, 13, 1, 55–69.

6. G. Oriolo, A. Luca and M. Vandittelli, WMR Control Via Dynamic Feedback Lineariza-

tion: Design, Implementation, and Experimental Validation, IEEE Transactions on Control

Systems Technology, 2002, 10, 6, 835–852.

7. C. Canudas de Wit and O. J. Sordalen, Exponential Stabilization of Mobile Robots with

Nonholonomic Constraints, IEEE Transactions on Automatic Control, 1992, 37, 11, 1791–

1797.

8. A. Luca, G. Oriolo and M. Vendittelli, Control of wheeled mobile robots: An experimental

overview, RAMSETE - Articulated and Mobile Robotics for Services and Technologies,

2001, S. Nicosia, B.Siciliano, A. Bicchi, P. Valigi, Springer-Verlag.

9. Y. Kanayama, Y. Kimura, F. Miyazaki and T. Noguchi, A stable tracking control method

for an autonomous mobile robot, Proceedings of the 1990 IEEE International Conference on

Robotics and Automation, 1990, 1, 384–389.

10. F. Pourboghrat and M. P. Karlsson, Adaptive control of dynamic mobile robots with non-

holonomic constraints, Computers and electrical Engineering, 2002, 28, 241–253.

11. T. C. Lee, K. T. Song, C. H. Lee and C. C. Teng, Tracking control of unicycle-modeled

mobile robots using a saturation feedback controller, IEEE Transactions on Control Systems

Technology, 2001, 9, 2, 305–318.

12. R. W. Brockett, Asymptotic stability and feedback stabilization, Differential Geometric Con-

trol Theory, 1983, R. W. Brockett, R.S. Millman and H. J. Sussmann, 181–191.