A New Model of Associative Memories Network
Roberto A. Vázquez and Humberto Sossa
Centro de Investigación en Computación-IPN
Av. Juan de Dios Batíz, esquina con Miguel Othón de Mendizábal
Mexico City, 07738, Mexico
Abstract. An associative memory (AM) is a special kind of neural network that
only allows associating an output pattern with an input pattern. However, some
problems require associating several output patterns with a unique input pattern.
Classical associative and neural models cannot solve this simple task. In this
paper we propose a new network composed of several AMs aimed to solve this
problem. By using this new model, AMs can be able to associate several output
patterns with a unique input pattern. We test the accuracy of the proposal with a
database of real images. We split this database of images into four collections
of images and then we trained the network of AMs. During training we
associate an image of a collection with the rest of the images belonging to the
same collection. Once trained the network we expected to recover a collection
of images by using as an input pattern any image belonging to the collection.
1 Introduction
An associative memory AM is a special kind of neural network that allows recalling
one output pattern given an input pattern as a key that might be altered by some kind
of noise (additive, subtractive or mixed). Several models of AMs are described in [1],
[2], [3], [5], [9], [10], [11] and [12]. In particular, models described in [5], [9] and
[10] cannot handle with mixed noise. Associative model presented in [11] and [12] is
robust to mixed noise.
An association between input pattern
x
and output pattern
y
is denoted as
()
,
kk
x
y
, where
k
is the corresponding association. AM
W
is represented by a
matrix whose component
ij
w
can be seen as the synapse of the neural network.
Operator
W
is generated from a finite a priori set of know associations, known as the
fundamental set of association and is represented as:
(
)
{
}
,1,,
kk
kp=xy …
where
p
is the number of associations. If
1, ,
kk
kp=∀=xy …
then
W
is auto-associative,
otherwise it is hetero-associative. A distorted version of a pattern
x
to be restored
will be denoted as
x

. If an AM
W
is fed with a distorted version of
k
x
and the
output obtained is exactly
k
y
, we say that recalling is perfect.
In this paper we present how a network of AMs can be used to recall nor just one
pattern but several of them given an input pattern. In this proposal an association
A. Vázquez R. and Sossa H. (2007).
A New Model of Associative Memories Network.
In Proceedings of the 3rd International Workshop on Artificial Neural Networks and Intelligent Information Processing, pages 3-12
DOI: 10.5220/0001634900030012
Copyright
c
 SciTePress

between input pattern
x
and a collection of output pattern
Y
is denoted as,
()
{}
,1,,
kk
kp=xY …
where
p
is the number of association,
{
}
1
,,
kr
=Y
yy
…
is a
collection of output patterns and
r
is the number of patterns belonging to collection
Y
.
The remaining of the paper is organized as follows. In section 2 we describe the
associative model used in this research. In section 3 we describe the proposed
network of AMs. In section 4 we present the experimental results obtained with the
proposal. In section 5 we finally present the conclusions and several directions for
further research in this direction.
2 Dynamic Associative Model
The brain is not a huge fixed neural network, as had been previously thought, but a
dynamic, changing neural network that adapts continuously to meet the demands of
communication and computational needs [8]. This fact suggests that some
connections of the brain could change in response to some input stimuli.
Humans, in general, do not have problems to recognize patterns even if these are
altered by noise. Several parts of the brain interact together in the process of learning
and recalling a pattern. For example, when we read a word the information enters the
eye and the word is transformed into electrical impulses. Then electrical signals are
passed through the brain to the visual cortex, where information about space,
orientation, form and color is analyzed. After that, specific information about the
patterns passes on the other areas of the cortex that integrate visual and auditory
information. From here information passes through the arcuate fasiculus, a path that
connects a large network of interacting brain areas; paths of this pathway connect
language areas with other areas involving in cognition, association and meaning, for
details see [4] and [7].
Based upon the above example we have defined in our model several interacting
areas, one per association we would like the memory to learn. Also we have
integrated the capability to adjust synapses in response to an input stimulus.
As we could appreciate from the previous example, before an input pattern is
learned or processed by the brain, it is hypothesized that it is transformed and codified
by the brain. In our model, this process is simulated using the following procedure
recently introduced in [11]:
Procedure 1. Transform the fundamental set of associations into codified patterns
and de-codifier patterns:
Input: FS Fundamental set of associations:
{1. Make
dconst=
and make
(
)
(
)
11 11
,,=xy xy
2. For the remaining couples do {
For
2k
=
to
p
{
For
1i =
to
n
{
1kk
ii
x
xd
−
=+
;
ˆ
kkk
iii
x
xx
=
−
;
1kk
ii
yy d
−
=
+
;
ˆ
kkk
iii
yyy
=
−
}}} Output: Set of codified and de-codifying patterns.
4

This procedure allows computing codified patterns from input and output patterns
denoted by
x
and
y
respectively;
ˆ
x
and ˆ
y
are de-codifying patterns. Codified and
de-codifying patterns are allocated in different interacting areas and d defines of much
these areas are separated. On the other hand, d determines the noise supported by our
model. In addition a simplified version of
k
x
denoted by
k
s
is obtained as:
(
)
kk
k
ss==xmidx
(1)
where mid operator is defined as
()
1/2 n
x
+
=
mid x
.
When the brain is stimulated by an input pattern, some regions of the brain
(interacting areas) are stimulated and synapses belonging to those regions are
modified.
In our model, we call these regions active regions and could be estimated as
follows:
() ()
1
arg min
p
i
i
ar r s s
=
⎛⎞
== −
⎜⎟
⎝⎠
xx
(2)
Once computed the codified patterns, the de-codifying patterns and
k
s
we can
build the associative memory.
Let
(
)
{
}
,1,,
kk
kp=xy …
,
kn
∈
xR
,
km
∈yR
a fundamental set of associations
(codified patterns). Synapses of associative memory
W
are defined as:
ij i j
wyx
=
−
(3)
After computed the codified patterns, the de-codifying patterns, the reader can
easily corroborate that any association can be used to compute the synapses of
W
without modifying the results. In short, building of the associative memory can be
performed in three stages as:
1. Transform the fundamental set of association into codified and de-
codifying patterns by means of previously described Procedure 1.
2. Compute simplified versions of input patterns by using equation 1.
3. Build
W
in terms of codified patterns by using equation 3.
2.1 Modifying Synapses of the Associative Model
As we had already mentioned, synapses could change in response to an input
stimulus; but which synapses should be modified? For example, a head injury might
cause a brain lesion killing hundred of neurons; this entails some synapses to
reconnect with others neurons. This reconnection or modification of the synapses
might cause that information allocated on brain will be preserved or will be lost, the
reader could find more details concerning to this topic in [6] and [13].
This fact suggests there are synapses that can be drastically modified and they do
not alter the behavior of the associative memory. In the contrary, there are synapses
that only can be slightly modified to do not alter the behavior of the associative
memory; we call this set of synapses the kernel of the associative memory and it is
denoted by
W
K
.
5

In the model we can find two types of synapses: synapses that can be modified and
do not alter the behavior of the associative memory; and synapses belonging to the
kernel of the associative memory. These last synapses play an important role in
recalling patterns altered by some kind of noise.
Let
n
∈
W
KR
the kernel of an associative memory
W
. A component of vector
W
K
is defined as:
(
)
,1,,
iij
kw w j m==mid …
(4)
According to the original idea of our proposal, synapses that belong to
W
K
are
modified as a response to an input stimulus. Input patterns stimulate some active
regions, interact with these regions and then, according to those interactions, the
corresponding synapses are modified. Synapses belonging to
W
K
are modified
according to the stimulus generated by the input pattern. This adjusting factor is
denoted by
wΔ
and can be computed as:
(
)
(
)
(
)
ar
wssΔ=Δ = −xx x
(5)
where
ar
is the index of the active region.
Finally, synapses belonging to
W
K
are modified as:
(
)
old
ww=⊕Δ−Δ
WW
KK
(6)
where operator
⊕
is defined as
1, ,
i
exei m
⊕
=+∀=x …
. As you can appreciate,
modification of
W
K
in equation 6 depends of the previous value of
w
Δ
denoted by
old
wΔ
obtained with the previous input pattern. Once trained the AM, when it is used
by first time, the value of
old
wΔ
is set to zero.
2.2 Recalling a Pattern using the Proposed Model
Once synapses of the associative memory have been modified in response to an input
pattern, every component of vector
y
can be recalled by using its corresponding input
vector
x
as:
(
)
,1,,
iijj
ywxjn=+=mid …
(7)
In short, pattern
y
can be recalled by using its corresponding key vector
x
or
x

in six stages as follows:
1. Obtain index of the active region
ar
by using equation 2.
2. Transform
k
x
using de-codifying pattern
ˆ
ar
x
by applying the
following transformation:
ˆ
kkar
=
+xxx

.
3. Compute adjust factor
(
)
wΔ=Δx

by using equation 5.
4. Modify synapses of associative memory
W
that belong to
W
K
by
using equation 6.
5. Recall pattern
k
y

by using equation 7.
6

6. Obtain
k
y
by transforming
k
y

using de-codifying pattern
ˆ
ar
y
by
applying transformation:
ˆ
kkar
=−yyy

.
The formal set of prepositions that support the correct functioning of this dynamic
model can be found in [14].
3 Architecture of the Network
Classical AMs (see for example [1], [2], [3], [5], [9], [10], [11] and [12]) are able to
recover a pattern (an image) from a noisy version of it. In their original form classical
AMs are not useful when image is altered by image transformations, such as
translations, rotations, and so on.
The network of AMs proposed in this paper is robust under some of these
transformations. Taking advantage of this fact, we can associate different versions of
an image (rotated, translated and deformed) to an image.
Our task is to propose a network of AMs aimed to associate an image with other
images belonging to the same collection. In order to achieve this, first suppose we
want to associate images belonging to a collection with an image of the same
collection using an AM. A good solution could be to compute the average image of
whole images belonging to the collection and then associate the average image with
any image that belongs to the collection. The same solution can be applied to other
collections. Once computed the average images from different collections and chosen
the images to be associated, we can train the AM as was described in section 2.
Until this point the AM only can recover an association between a collection of
input patterns
X
and output pattern
y
denoted as,
(
)
{
}
,1,,
kk
kp=Xy …
where
p
is the number of association,
{
}
1
,,
kr
=Xx x…
is a collection of input patterns and
r
is the number of patterns belonging to collection
X
. This means that it can only be
recovered the associated image using any image from a collection. However, we
would like to get the inverse result; instead of recovering the associated image using
any image from a collection, we would like to recover all the images belonging to the
collection using any image of the collection.
To achieve this goal we will train a network of AMs built as in previous sections.
Each AM will associate all the images of a collection with one image of this
collection. This implies that for recovering all images of a given collection, we would
need
r AMs, where r is the number of images belonging to the collection. The
network architecture of AMs needed for recovering a collection of images is shown in
Fig. 1.
In order to train the network of
r AMs, first of all we need to know the number of
collections we want to recover. Training phase is done as follows:
1. Transform each image into a vector.
2. Build
n
collections of images
n
qr
×
⎡
⎤
⎣
⎦
CI
where
q
is the number of
pixels of each image and
r
the number of images.
7

3. Let
[
]
qn
×
AI
a matrix of average images. For
1k
=
to
n
compute the
average image as:
1
r
k
s
s
k
r
=
=
∑
CI
AI
(8)
4. For
1
s
=
to
r
build an
s
AM
as described in Section 2.2. For
1k =
to
n
k
k
=xAI
and
kk
s
=yCI
Once trained the network of AMs, when is fed with any image of a collection,
each AM will respond with an image that belongs to the collection. To recover a
collection of images we just operate each AM with the input image as described in
Section 2.3.
Fig. 1. Architecture of a network of AMs for recalling a collection of patters using an input
pattern.
4 Experimental Results
In this section the accuracy of the proposal is tested using different collections of
images shown in Fig. 2.
(a) (b) (c) (d) (e)
Fig. 2. (a-e) Collections of images taken from the Amsterdam Library of Objects Images
(ALOI).
Twenty complex images were grouped into five collections composed by four
images, see Fig. 2. After that, we proceeded to train the network of AMs as was
8

explained in Section 3. For this problem our network is composed of four AMs. It is
important to say that the number of images composing a collection could by any, the
only restrictions to guaranty perfect and robust recall is that patterns (images) satisfy
propositions described in [14].
Once trained the network, four experiments were performed to test the accuracy of
the proposal. The first experiment consisted on recovering a collection of images
using any image of the collection in order to verify how much robust is the proposal
under image deformations. Second experiment consisted on recovering a collection of
images using any image of the collection altered by mixed noise in order to verify
how much robust is the proposal under deformations and noisy version of the images.
In the third experiment each image of the training set was rotated (from 0 to 360). We
then used them to fed the network of AMs in order to verify how much robust is the
proposal under deformations and rotations. Finally for forth experiment the images of
the training set were rotated (from 0 to 360) and translated, and then used them to fed
the network of AMs in order to verify how much robust is the proposal under
deformations, rotations and translations.
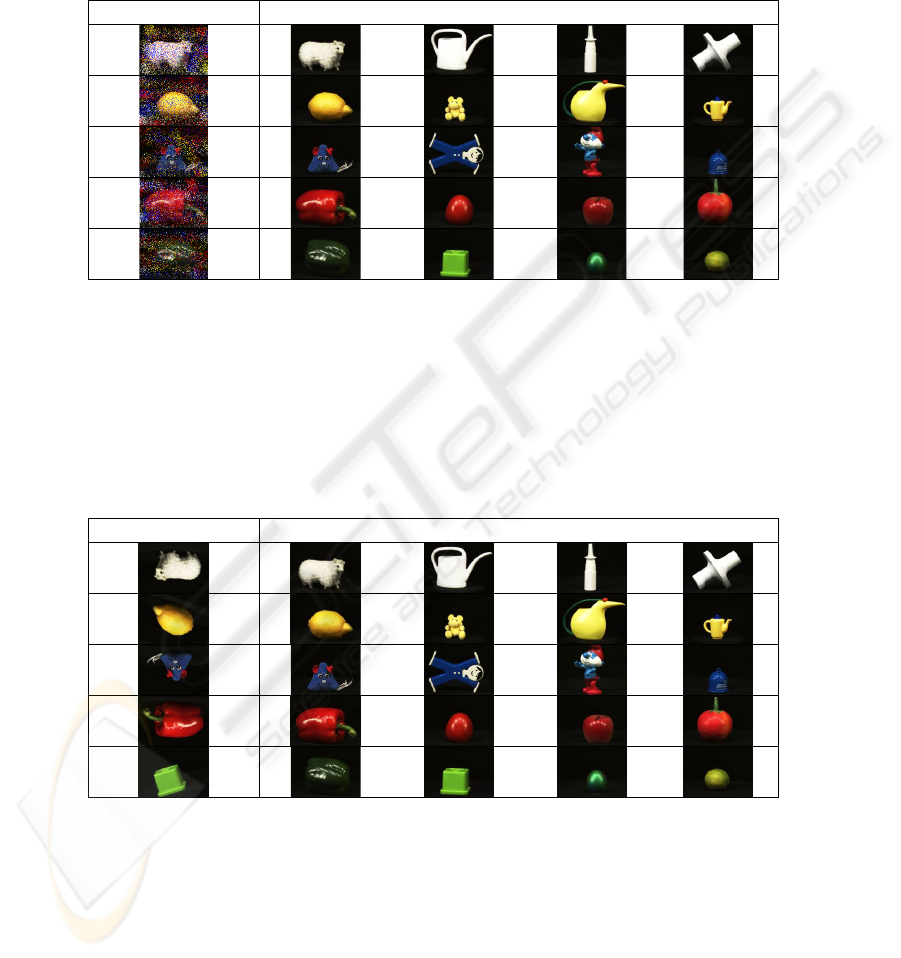
The accuracy of the proposal was of 100% in the first experiment. The five
collections of images where perfectly recovered by using any image of the collection
(20 images), in Table 1 are shown some results obtained in this experiment.
Remember that we train the network of AMs with average images, so then; when we
fed the network with an image of any collection this image could be seen as a
deformed version of the average images. The results provided by our proposal in this
experiment show that the associative model used to train the network of AMs is
robust under deformations. Something important to say is that if we use other
associative models for training the network of AMs such as morphological or median
AMs, the collections might not be correctly recovered due to they are not robust under
these kind of transformations or deformations.
Table 1. Some results obtained for the first experiment. As you can appreciate all sets of
images were perfectly recovered.
Input image Image recovered by each AM.
The accuracy of the proposal, in the second experiment, was of 100%. The five
collections of images where recovered perfectly by using any image of the collection
even when this images were altered by noise (200 images). As you can see in Table 2,
despite of the level of noise add to the images, the collections were correctly
9

recovered. Despite of other associative models are robust to this kind of noise, they
might not recover the all collections due to they are only robust under additive,
subtractive and mixed noise but not to deformations.
Table 2. Some results obtained for the second experiment. Despite of the noise added to the
images, all sets of images were again correctly recovered.
Input image Image recovered by each AM
The accuracy of the proposal, in the third experiment, was also of 100%. The five
collections of images where recovered perfectly even when rotated version of the
images were used (700 images), see in Table 3. Some important to say is, to our
knowledge, neither morphological AMs nor other classical models are robust under
rotations. Due to we used simplified patterns using mid operator and due to this
operator is invariant to rotations the accuracy of the proposal was of 100%.
Table 3. Some results obtained for the third experiment. Despite of the noise added to the
images and rotations, all sets of images were again correctly recovered.
Input image Image recovered by each AM
Finally, the accuracy of the proposal, in the forth experiment was of 40%. In this
experiment with 700 images; with some images we recall a collection, but with some
other images (when patterns do not satisfied the proposition which guarantee robust
recall) the collections were not recalled, see Table 4. However, the results obtained by
our proposal are acceptable if they are compared with the results provided by order
associative models (less of 10% of accuracy).
10

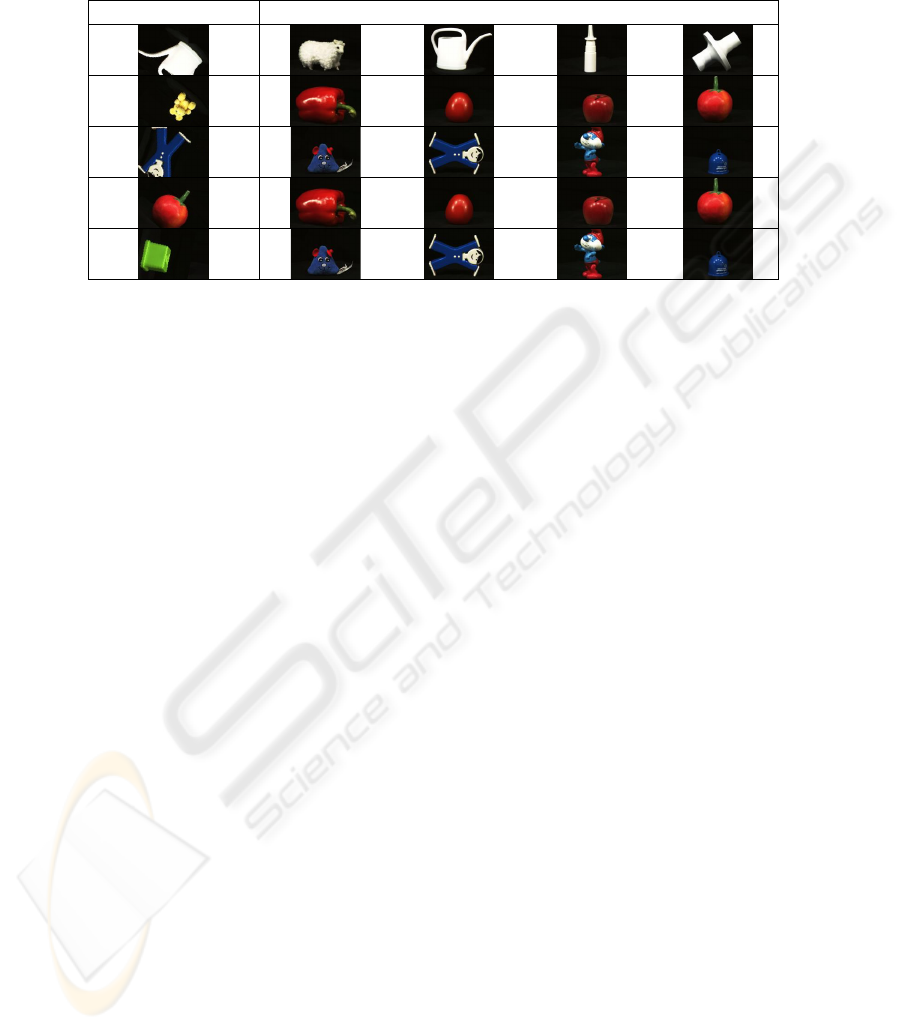
Table 4. Some results obtained for the forth experiment. With some images we recall a
collection, but with some other images (when patters do not satisfied the proposition which
guarantee robust recall) the collections was not recalled.
Input image Image recovered by each AM
In general, the accuracy of the proposal with different banks of images (altered by
noisy and rotated) was of 100%. This was due to the input patterns (the images)
satisfy the propositions presented in [14]. If these patterns do not satisfy these
propositions, as images used in experiment four (translated and rotated images), the
accuracy of the proposal diminish. However, the results provided by our proposal up-
performed the results provide by other associative models.
5 Conclusions and Directions for Further Research
In this paper we have proposed a network of AMs. This network is useful for
recalling a collection of output patterns using an input pattern as a key. The network
is composed by several dynamic associative memories (DAM). This DAM is
inspirited in some aspects of human brain. The model, due to plasticity of its synapses
and functioning, is robust under some transformations as rotation, translation and
deformations.
In addition, we describe an algorithm for training a network of AMs codifying the
images of a collection by using an average image. Once computed the average images
we proceed to training the network of AMs.
The network is capable to recall a collection of images (patterns) even if images
are altered by noise or suffer some deformations, rotations and translations.
Through several experiments we have shown the efficiency of the proposal. In the
first three experiments the proposal provided an accuracy of 100%. Even when the
images were altered with mixed noise and rotated, the network of AMs recovered the
corresponding collection. When object in images suffer translations, the accuracy of
the proposal diminish. This is because most of the patterns under this transformation
do not satisfied the propositions that guarantee robust recall. However, the results
provided by our proposal up-performed the results provide by other associative
models.
The performed experiments could be seen as an application for image retrieval
problems. We could say that we have developed a small system able to recover a
11

collection of images (previously organized), even in the presence of altered versions
of the images.
Nowadays we are working and directed this research to solve real problems in
images retrieval system. We are focusing our efforts to propose new associative
models able to associate and recall images under more complex transformations.
Furthermore, this new models have to work with images of much more complicated
objects such as flowers, animals, cars, faces, etc.
Acknowledgements
This work was economically supported by COTEPABE-IPN, SIP-IPN under grant
20071438 and CONACYT under grant 46805.
References
1. K. Steinbuch. 1961. Die Lernmatrix. Kybernetik, 1(1):26-45.
2. J. A. Anderson. 1972. A simple neural network generating an interactive memory.
Mathematical Biosciences, 14:197-220.
3. J. J. Hopfield. 1982. Neural networks and physical systems with emergent collective
computational abilities. Proceedings of the National Academy of Sciences, 79: 2554-2558.
4. M. Kutas and S. A. Hillyard. 1984. Brain potentials during reading reflect word expectancy
and semantic association. Nature, 307:161–163.
5. G. X. Ritter el al. 1998. Morphological associative memories. IEEE Transactions on Neural
Networks, 9:281-293.
6. Iva Reinvan. 1998. Amnestic disorders and their role in cognitive theory. Scandinavian
Journal of Psychology, 39(3): 141-143.
7. C. J. PRICE. 2000. The anatomy of language: contributions from functional neuroimaging.
Journal of Anatomy, 197(3): 335-359.
8. S. B. Laughlin and T. J. Sejnowski. 2003. Communication in neuronal networks. Science,
301:1870-1874.
9. P. Sussner. 2003. Generalizing operations of binary auto-associative morphological
memories using fuzzy set theory. Journal of mathematical Imaging and Vision, 19(2):81-
93.
10. G. X. Ritter, G. Urcid, L. Iancu. 2003. Reconstruction of patterns from noisy inputs using
morphological associative memories. Journal of mathematical Imaging and Vision,
19(2):95-111.
11. H. Sossa, R. Barrón, R. A. Vázquez. 2004. Transforming Fundamental set of Patterns to a
Canonical Form to Improve Pattern Recall. LNAI, 3315:687-696.
12. H. Sossa, R. Barrón, R. A. Vázquez. 2004. New associative memories for recall real-valued
patterns. LNCS, 3287:195-202.
13. K. D. Jovanova-Nesic and B. D. Jankovic. 2005. The Neuronal and Immune Memory
Systems as Supervisors of Neural Plasticity and Aging of the Brain: From Phenomenology
to Coding of Information. Annals of the New York Academy of Sciences, 1057: 279-295
14. R. A. Vázquez and H. Sossa. 2007. A new associative memory with dynamical synapses.
Submitted to IJCNN 2007.
12