Multi-Robot Task Allocation with Tightly Coordinated

Tasks and Deadlines using Market-Based Methods

Robert Gaimari, Guido Zarrella and Bradley Goodman

The MITRE Corporation, 202 Burlington Road, Bedford MA 01730, USA

Abstract. The domain of Collaborative Time Sensitive Targeting requires

agents to assess and prioritize tasks, dynamically form heterogeneous teams of

agents to perform the tightly coordinated tasks, and to complete them within

time deadlines. In this paper, we describe extensions to market-based, multi-

robot task allocation to allow for these requirements.

1 Introduction

The motivation for the research described in this paper is to extend the state of the art

in market-based multi-robot planning algorithms to handle the challenges presented

by real world domains with tightly-coordinated and time-constrained tasks. Past

research into market-based robot coordination algorithms [2, 3, 11] has been

motivated by an attempt to design an algorithm to reason in an efficient fashion about

resource utilization and task allocation while preserving the ability to quickly and

robustly respond to a dynamic environment.

Prior work has demonstrated the effectiveness of the TraderBots algorithms [2, 3]

in several domains. It has been used in domains with tightly coordinated tasks

requiring heterogeneous, dynamically formed teams [7]. It has also been used in

domains requiring homogeneous teams to perform tasks with time deadlines [8].

There are other real world applications that bring together elements from both of these

areas. The Collaborative Time Sensitive Targeting (TST) problem, for instance, is a

domain in which agents must assess and prioritize multiple tasks, form heterogeneous

teams dynamically, and perform tightly-coordinated tasks with tight deadlines. Search

and rescue is one real-world example of a TST problem. Multiple rescue workers,

each having different skills, must work together to save the maximum number of

victims within a limited time period. New information will be discovered during the

rescue, forcing the workers to reassess and reprioritize.

The TST domain requires tightly-coupled coordination between agents, as agents

with complementary capabilities are required to form sub-teams in order to

successfully perform a task. The TST domain also requires agents to reason about

tasks with time deadlines.

Section 2 of this paper explains our task domain, a type of TST problem. Section 3

describes the standard approach of market-based, multi-robot task allocation, as

Gaimari R., Zarrella G. and Goodman B. (2007).

Multi-Robot Task Allocation with Tightly Coordinated Tasks and Deadlines using Market-Based Methods.

In Proceedings of the 3rd International Workshop on Multi-Agent Robotic Systems, pages 54-63

 SciTePress

presented in [2]. Section 4 describes our implementation in detail, along with our

extensions to the standard approach. And in Section 5, we show our results.

2 Task Domain

Our task domain is a variant of the TST problem. In our scenario, autonomous robots

perform a Search and Rescue mission by locating and treating sick sea animals. Over

the course of an exercise (90 “minutes” long, sped up in the simulation), messages

come in from outside the system with reports of the general locations where sick

animals might be found. These animals move over time. The message will list the

name of the animal (e.g. “Sick Manatee”), the approximate latitude-longitude location

(either a single point, or an area of ocean), a deadline which the task has to be

completed by (e.g. cure the manatee within 30 minutes or it will die), and the

maximum reward offered for completing the task. If a task is completed before the

deadline, the robots receive the full reward; if the deadline passes, they receive no

reward, even if they complete the task. The robots already have an incentive to finish

tasks as quickly as possible; the faster they complete one task, the faster they can

begin a new one. If we wanted to make finishing as quickly as possible even more

important, we might allow the maximum reward to drop as the deadline approached,

gradually falling to zero.

In this domain, all tasks are of equal priority; therefore, the maximum rewards are the

same for all tasks. If we wanted to indicate that some tasks have higher priority than

others, we could set some rewards higher than others, making them more valuable to

perform.

We have a heterogeneous set of robots available to perform these jobs. They are in

three main groups:

1. Radar Sensors – Planes and boats with radar and sonar sensing capabilities. They

are very fast and have large sensing range; so they can get to the location quickly

and easily pinpoint where the animal is located. However, since they are sensing

electronically, they cannot diagnose the illness.

2. Video Sensors – Planes, boats, and helicopters with video sensing capabilities.

Because they have video, they are able to diagnose the disease the animal has and

report it to the rest of the team. However, they are very slow and have limited

sensing range.

3. Rescue Workers – Boats or submarines capable of capturing or curing animals in

distress. They are generally about as fast as radar sensors. However, they have no

sensors of their own; they must rely on reports from the sensor robots for

navigation data. Also, they can act only with the proper diagnosis from a video

sensor.

The robots within each group vary in their specific characteristics, such as speed and

sensing range. Also, there are three separate areas of ocean to be searched; the set of

robots on each map is confined to that area. Initially, some robots are stationary near

their home base and will remain there until they receive a task; others have initial

paths that they follow once the clock begins, whether they have a task or not.

To complete a task, there must be a minimum of two robots: a video sensor to find the

animal and make the diagnosis, and a rescue worker to administer the treatment. A

radar sensor is not required, but because of its speed and sensor range, it can reduce

the cost of finding the animal.

3 Market-Based Task Allocation

In a market-based system, such as the one described in [2], the problem space is

modeled as an economy. The currency may be simply an abstract measure, or it may

represent something concrete, such as time, fuel, resources, etc. It represents the value

of performing tasks and achieving goals.

There are a set of tasks which need to be performed. These tasks will generally take

one or a group of agents to complete. Each task is a source of revenue for the agents;

each has a monetary reward associated with it, which is given to the agent(s) that

successfully complete the task. These rewards vary according to a number of

measures, such as relative priority, difficulty, risk, etc.; they are set at the beginning

of the exercise, generally by the human assigning the tasks. Performing a task also

costs an agent a certain amount of money, as resources must be consumed to complete

them.

The players in this economy are the robots. They may be physical or virtual,

depending upon the jobs they must do. In a homogenous group, all of the robots have

the same capabilities and any job may be done by any robot. More complex systems

may be made up of heterogeneous groups. In these systems, jobs may require several

robots working together as a team to complete the mission. Individual agents are

“self-interested”; that is, each agent works to earn as much profit as possibly by

minimizing its own costs and maximizing its own revenue. The goal of the system as

a whole is to minimize the cost of resources consumed by the team while maximizing

the value of the tasks completed. Free market economic theory holds that a collection

of self-interested agents will self-organize through spontaneous cooperation and

competition to create an emergent, globally efficient behavior. Market-based planning

algorithms seek to mimic this behavior with a simulated economy.

Tasks are distributed through auction. As each task is introduced to the system, it is

given to a special type agent called an “OpTrader”. An OpTrader sends out an

announcement to all of the participating robots describing the task and the maximum

reward available for performing the task. This is the call for bids. Each robot

interested in placing a bid for the job does three things:

1. Calculate the estimated cost for performing the task. In a domain where there is no

ambiguity, the robot may be able to determine exactly how much performing the

task will cost. But in most realistic systems, there will be hidden information that

will not be revealed until the task is already under way. For example, there may be

unknown obstacles between the robot’s current location and the destination; or the

destination may only be partially defined.

2. Calculate the desired profit. The profit must be high enough to make it worth the

robot’s time to perform the task. The robot must decide how much payment it will

require to make the task worthwhile. A common method for calculating a profit

margin is to use a set percentage of the costs or available revenue.

3. Calculate the bid. This is generally the cost plus the profit margin. If this bid

amount is lower than the maximum reward available, then send it to the auctioneer.

The OpTrader will gather all of the bids and award the ownership of the task to the

robot with the lowest bid. The difference between the maximum reward and the

lowest bid is kept by the OpTrader as its profit.

Once the initial round of bids is completed, and all tasks have been awarded, each

robot that owns a task may decide to put it up for another round of auction. Now that

each robot has a plan of where it will be going and what it will be doing, it can have a

better idea of its costs for performing other tasks. If it has already committed to

performing a task in a certain location, then it might be relatively inexpensive to also

perform another task in the same area. Inter-robot trading (reauctioning) allows the

tasks to be redistributed to the robots that can perform that at lower costs. To

complete such a deal both robots must be happy with the exchange – the buyer robot

has a new task at low cost, and the seller robot has a nice profit (the difference

between the maximum reward it announced and the buyer’s bid) for no extra work.

This inter-robot trading will continue until there are no more mutually profitable deals

to be made, at which time the robots will begin performing their tasks. As they move

and explore the environment on their paths, they will be gathering additional

information on the environment. As new and more accurate data becomes available,

the robots may periodically put some of the tasks on their agendas up for reauctioning

again; others may have discovered things that would allow them to more accurately

estimate cost and buy the tasks from the seller.

When a robot completes a task, it sends a message to the agent it bought the task

from, requesting payment. That agent will send a message up the chain to the next

level where it got the task from, and so on. Once it reaches the top (the OpTrader),

payments will work their way back down the chain, until each robot along the way

has been paid what it was promised.

Auction-based task assignment and multi-robot coordination allows the system to

approach an approximation of the optimal solution of minimal cost and maximal

reward while keeping communication costs relatively low, avoiding single points of

failure, and robustly handling robot failure and communication difficulties.

4 Implementation and Extensions

We developed our simulation and agent environment entirely in Java using the JADE

agent framework [1]. Task allocation through auction was handled using inter-agent

communication. The market-based task allocation is performed using the methods

described in Section 3, with our extensions.

4.1 Agents

The primary type of agent in our system is the TraderAgent. Each TraderAgent is

associated with a single robot in the simulation environment. When they are first

initialized, TraderAgents have a back and forth communication with their assigned

robots to learn their capabilities (what type of robots they are, their speeds, sensing or

rescue ranges, and so on) and current status (their current locations, their remaining

fuel, and, in the case of sensors, lists of objects detected and their locations). Each

clock tick of the environment thereafter, each robot will send its agent the latest status

report. If the TraderAgent wants its robot to move to a new location, it sends a

message directing it on the new path.

A TraderAgent’s primary job, as the name implies, is to trade tasks. When a new task

is announced, an agent may attempt to buy it through auction. This process is

described in Section 4.2. An agent which owns a task may put it up for auction, either

to off-load the task to a new robot, or in team building. These re-auctioning methods

are described in Section 4.3.

When tasks are introduced to the system, they are initially given to the special

OpTrader agent. This agent differs from a standard TraderAgent only in that it does

not have a robot associated with it. The OpTrader immediately puts tasks given to it

up for auction, with a maximum offered reward that is part of the task description.

When the task is completed, it is responsible for sending the payment for the job to

the original purchasing agent. Because it is not associated with a robot, it cannot be a

member of a team. In a system where robustness is essential, there could easily be

multiple copies of these agents, either ready to take over in the event of a problem or

performing their jobs in parallel with their counterparts; however, in our system, one

of each is sufficient.

4.2 Bidding on Auctions

When a TraderAgent receives an auction announcement, it follows the three steps

described Section 3, on standard auction-based systems.

1. The agent calculates its estimated cost for performing the task. In our system, cost

is based upon the time spent performing the task. The locations given in the

auction message are general locations, not specific; once sensors arrive there, there

may need to be some exploration before finding the actual animal. Also, this cost

may be affected by other locations that the agent already intends to visit. If the new

area is nearby somewhere the agent is already headed, the estimated cost for the

new task would be lower.

2. It calculates the desired profit. The TraderAgent calculates, as its base profit, a

percentage of the difference between the maximum reward offered and its

estimated cost. In addition, an opportunity cost for accepting the task is calculated.

This represents the likelihood that the agent will be able to purchase other tasks at

a future date. The agents know the locations and capabilities of other nearby robots

with similar capabilities, since this information is periodically broadcast locally.

The agent selects a number of random locations on the map and simulates how

many of these locations it would be likely to win in a hypothetical auction. This

represents opportunity cost. An agent with a high OC can safely lose out on the

current auction without fearing for its own economic well-being. Therefore, a high

OC agent is able to request a higher profit margin. Meanwhile agents in less

desirable circumstances are willing to lower their profit margin in an attempt to

win the current auction. This means that the lowest cost agent may not always win

an auction, particularly in cases where the overall team can benefit by saving a

high OC agent for future tasks. We apply this opportunity cost function to help

prevent over-committal of scarce resources.

3. The TraderAgent decides whether or not to place the bid, based upon cost plus

desired profit. If this value is less than the maximum reward, then it places the bid.

If the value is higher than the maximum reward, or if the TraderAgent realizes it

cannot complete the task in the required amount of time (causing the task to be

finished after the task deadline), it will decide not to place a bid and it sends a “no

thanks” message to opt out of the auction.

4.3 Re-Auctioning Tasks

There are two situations in which an agent will attempt to re-auction a task it owns

but has not yet completed. The first is in the team building stage. This step is critical

to robots performing tightly coupled tasks. After a robot wins a task at auction, it is

sent a list of other robots that already have ownership of the task. These robots make

up the team that will eventually perform the task. If the team is not yet complete, for

instance if no rescue worker has joined the team, the robot will place this task on the

auction block with a caveat that it is only accepting bids from a certain type of buyer.

At the conclusion of the auction, the winning bidder is assigned ownership of the task,

but the seller retains ownership as well, and all members of the team update their

team lists.

Robots will also periodically attempt to place tasks they own up onto the auction

block for the purposes of offloading the task onto another robot. In this case the task

can only be sold to a robot with the same capabilities as the seller. If there are no bids

the seller retains ownership of the task. On the other hand, if new information has

arrived and cost estimates have been updated, a different robot may choose to buy the

task. This will occur only when the new robot is willing to charge less to perform the

task than the seller’s expected costs, allowing both robots to earn a profit. In this case,

the winning bidder replaces the seller on the original team list, and the seller is freed

of its obligation.

4.4 Collecting Payment for Completed Tasks

As described earlier, the tasks in this system must be performed by a team of robots

including at least one video sensor and rescue worker. This team can also optionally

include a radar sensor. The rescue worker is the robot that actually finishes the task,

which it accomplishes by administering medicine curing the animal. Once the rescue

worker has done this, its TraderAgent reports the fact to its teammates. Each

teammate then requests payment from the agent that it purchased the task from.

Our system varies in this regard, however, from the standard auction-based algorithm.

In our task the teams are made up of robots that perform their jobs at greatly different

speeds. Even though the estimated cost for a radar sensor may be very low, the actual

cost is greatly increased by having to wait around while the slow video sensor travels

to the location and does its own part of the job. Since the agents associated with fast

robots generally win the tasks before the slower ones, there is no way to know ahead

of time what the additional costs might be.

There are a number of ways that this inefficiency could be dealt with. For example,

we could include information about slower robots in the cost estimation functions of

each TraderAgent. Another option would be to have the agents, once a team is

completed, share their cost estimates and allow the faster ones to recalculate. We

chose a method that requires a lower amount of inter-robot communication, in which

agents incur penalties on the agents below them in the chain.

The request for payment is the same. Each agent requests the amount of money it bid

for the task from the agent it bought the task from. However, as the payments are

distributed down the chain, each agent compares the actual cost to the estimated cost

it had initially planned upon. The difference between these is deducted from the

amount paid to the next agent. This agent adds, as a penalty to the next agent down,

the difference in its actual cost and the cost estimate, plus the amount it was penalized

by its seller. This penalty will move down the chain, until it finally winds up where it

belongs, on the slowest member of the team. These payments reflect the amount of

money the original agents would have bid if they had known the true cost based upon

the slowest robot. See an example in Figure 1. This example assumes that there was

no inter-robot trading or adding and removing of team members, but the details would

be essentially the same even with other agents in the chain. Future versions of the

algorithm may be able to use these penalties to learn the hidden costs of working with

certain other robots.

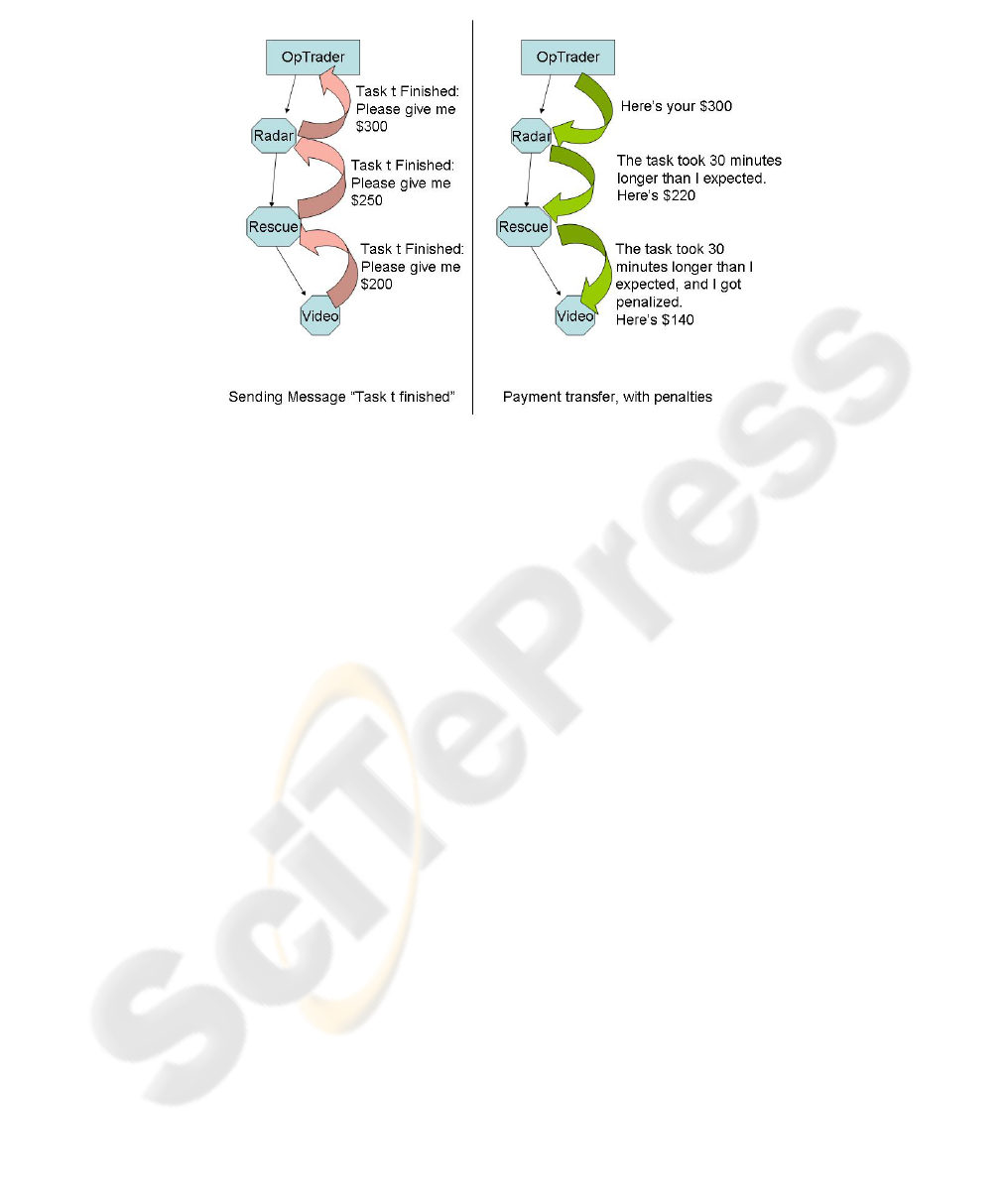
Fig. 1. Task Completion.

5 Results

The TST domain provides an ideal testbed for the market-based task allocation

algorithm, since completion of each TST task requires effective communication and

task assignment strategies. Furthermore the TST problem provides clear metrics for

evaluating group performance, as we can measure both the percentage of tasks

completed and the time needed to complete each task. We use this domain to

demonstrate our hypothesis that as the self-interested agents earn money in the virtual

economy, they also contribute toward the team goals and overall group performance,

even when performing tightly coupled tasks under pressure of time deadlines.

We built a test problem for our robot planning algorithm by performing a direct

translation of tasks used in a set of human experiments we performed into our own

modified aquatic TST domain. The translation was completely isomorphic, meaning

that the speeds, positions, and other attributes of all elements of the environment were

identical. Only the labels and images were changed for the purposes of the demo. The

robots planned and executed their own actions for 90 simulated minutes while

following the rules of the team-based economic system outlined above. A total of six

tasks were fed electronically at timed intervals into the robot auction environment.

The results of the robot and human teams are displayed in Table 1. The results show

that the robots were able to demonstrate effective team building and task assignment

strategies. The team of robots completed five of the six tasks with plenty of time to

spare before the task deadlines.

Table 1. Time (hh:mm:ss) to complete each task, comparing market-based robot task allocation

algorithm and human team performance.

Task:

Manatee

Killer

Whale

Blue

Whale

Dolphin

Sea

Turtle

Toxic

Leak

Robot

Completion

Time

0:42:00 0:40:00 1:22:00 1:09:00 1:07:00 N/A

Avg

Human

Team

Completion

Time

0:56:12 0:59:39 1:21:24 N/A 1:20:36 N/A

The robot team results also compare very favorably to the human teams’ results. The

robots completed five of six tasks, while no human team completed more than four.

The agents were able to complete the Dolphin task, which none of the ten human

teams had successfully prosecuted. The robots were also significantly faster than the

best human teams in three of the four tasks that were solved by both humans and

robots. The simulated agents did fail to complete one task, but none of the human

teams were able to successfully complete that task either. For more details on the

human version of the experiment, and comparing human/robot results, see our paper

submitted to the main conference.

6 Conclusion

We have shown that market-based multi-robot task planning can be successfully

extended into domains requiring tightly-coordinated actions to solve tasks with time

deadlines. In the case of our simplified TST domain, teams of autonomous robots

were able to provide significant gains over the performance of teams of humans.

We are not suggesting removing humans from the loop of the TST process. In real

world TST of any kind, there are many decisions that cannot possibly be made

without humans. Instead, our hope is that lessons learned from this research that can

be applied to real world problems.

Acknowledgements

The MITRE Technology Program supported the research described here. We are also

grateful for the assistance of Brian C. Williams and Lars Blackmore at the

Massachusetts Institute of Technology

References

1. Bellifemine F., Poggi A., Rimassa G. (2001). Developing multi-agent systems with a FIPA-

compliant agent framework. Software-Practice and Experience, 31, 103–128.

2. Dias M.B. (2004). TraderBots: A New Paradigm for Robust and Efficient Multirobot

Coordination in Dynamic Environments. Doctoral dissertation, Robotics Institute, Carnegie

Mellon University.

3. Dias M.B., Zlot R.M., Zinck M.B., Gonzalez J.P., Stentz A. (2004). A Versatile

Implementation of the TraderBots Approach for Multirobot Coordination. Retrieved from

www.ri.cmu.edu/pubs/pub_7477.html

4. Gerkey B., Mataric M. (2004). Multi-robot Task Allocation: Analyzing the Complexity and

Optimality of Key Architectures. International Journal of Robotics Research, 23 (9).

5. Goodman B., Linton F., Gaimari R., Hitzeman J., Ross H., Zarrella G. (2005). Using

Dialogue Features to Predict Trouble During Collaborative Learning. User Modeling and

User-Adapted Interaction, 15 (1-2), 85-134.

6. Grunwald T., Clark D., Fisher S. S., McLaughlin M., Narayanan S., Piepol D. (2004).

Using Cognitive Task Analysis to Facilitate Collaboration in Development of Simulator to

Accelerate Surgical Training. Studies in Health Technology and Informatics, 98, 114-120.

7. Jones E., Browning B., Dias M. B., Argall B., Veloso M., Stentz A. (2006, May).

Dynamically Formed Heterogeneous Robot Teams Performing Tightly-Coordinated Tasks.

Proceedings of International Conference on Robotics and Automation.

8. Jones E., Dias M. B., Stentz A. (2006, October). Learning-enhanced Market-based Task

Allocation for Disaster Response. Tech report CMU-RI-TR-06-48, Robotics Institute,

Carnegie Mellon University.

9. Lagoudakis M., Markakis E., Kempe D., Keskinocak P., Kleywegt A., Koenig S., Tovey

C., Meyerson A., and Jain S. (2005). Auction-based multi-robot routing. Robotics: Science

and Systems. Retrieved from http://www.roboticsproceedings.org/rss01/p45.pdf

10. Schneider J., Apfelbaum D., Bagnell D., Simmons R. (2005). Learning Opportunity Costs

in Multi-Robot Market Based Planners. IEEE Conference on Robotics and Automation.

11. Walsh W., Wellman M., Wurman P., MacKie-Mason J. (1998). Some Economics of

Market-Based Distributed Scheduling. International Conference on Distributed Computing

Systems. 612-618.